Symétries C, P, T (et leurs combinaisons)

Au 20e siècle, les experts en physique des particules ont découvert qu'il est très important de prendre en compte toutes les symétries possibles qui peuvent être démontrées par les lois de la nature qui régissent les particules élémentaires. La présence ou l'absence de symétrie peut nous révéler des aspects de la nature qui autrement ne sont pas évidents.

Parmi les nombreuses symétries possibles, trois peuvent jouer un rôle unique: conjugaison de charges (C), parité spatiale (P) et symétrie par rapport à l'inversion temporelle (T). Trois de ces transformations, affectant les particules, l'espace et le temps, comprennent:

• C: remplacer toutes les particules par des particules de charge opposée (à la fois une charge électrique et des charges moins connues; même certaines particules neutres sont remplacées. Par exemple, les neutrinos se transforment en antineutrinos et les neutrons en antineutrons).
• P: placer le monde dans un miroir (plus précisément, changer l'orientation des trois dimensions à l'opposé).
• T: lancer le monde dans le sens inverse du temps (plus précisément, changer le sens de l'évolution temporelle).

Chacune de ces transformations a la propriété que si vous la réalisez deux fois, vous reviendrez à l'état d'origine. Dans le jargon, nous disons que P ² = P × P = 1 (c'est-à-dire que si vous mettez un miroir dans un miroir, ce que vous voyez aura la même apparence que s'il n'y avait pas de miroir), et, de même, C ² = 1 et T ² = 1.

De plus, vous pouvez effectuer deux conversions ensemble. Par exemple, vous pouvez créer C, puis P, que nous écrivons simplement comme «CP» (ou vous pouvez faire PC, ce sera le même - l'ordre n'a pas d'importance pour ces transformations), dans lequel vous mettez le monde dans le miroir et changez charges de particules. Vous pouvez considérer CT, PT et même CPT. Ainsi que C, P et T eux-mêmes, n'importe laquelle de ces combinaisons, une fois effectuée deux fois, renverra tout comme il était.

Et que faisons-nous de ces transformations? Nous devons poser une question: si nous imaginons un monde créé à partir du nôtre en utilisant l'une des transformations, les lois de la nature qui régissent les particules et les interactions élémentaires fonctionneront-elles de la même manière que la nôtre?

Si la réponse est oui, alors tout ce qui peut se produire dans un nouveau monde transformé peut se produire dans le nôtre; dans ce cas, nous disons que cette transformation est la symétrie de notre monde. Plus précisément, c'est la symétrie des lois de la nature de notre monde. Sinon, alors la transformation peut encore être effectuée, mais ce ne sera pas la symétrie de notre monde, car le monde obtenu après la transformation sera différent du nôtre.


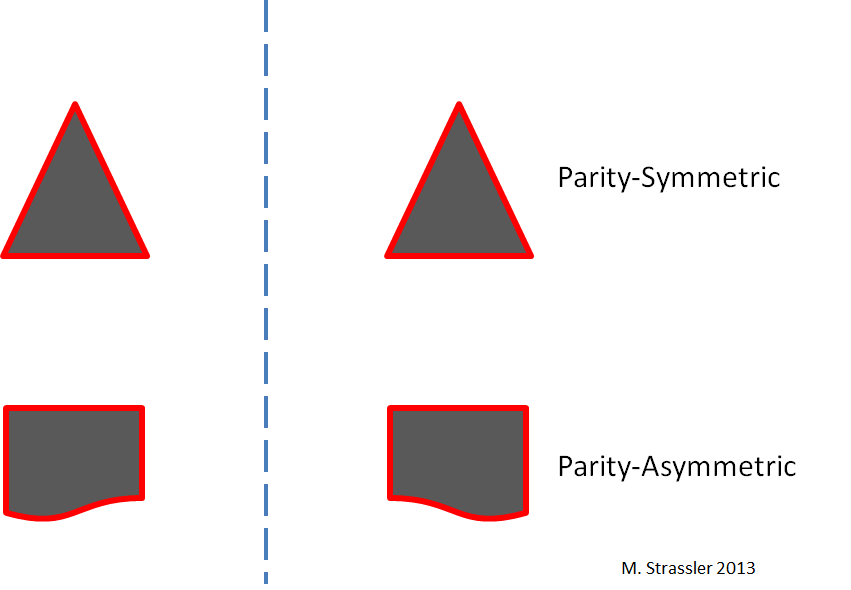Fig. 1

Il est assez facile de comprendre comment fonctionne la parité spatiale (P). Un objet particulier peut avoir ou non une symétrie de parité. Comme le montre la fig. 1, la réflexion d'un triangle dans le miroir nous donne un triangle identique au premier, de sorte que le triangle sera symétrique en parité. Mais une forme plus complexe, représentée au bas de la fig. 1, n'a pas exactement la même apparence après réflexion, il est donc asymétrique en parité.

Évidemment, notre monde n'est pas symétrique dans le miroir; cela peut être vu dans n'importe quelle photographie de la nature (voir Fig.2). Il faut cependant distinguer entre la symétrie de l'objet et la symétrie des lois de la nature qui régissent tous les objets possibles. Les processus de base de la physique des particules peuvent être symétriques, ce qui signifierait que pour tout processus qui peut se produire dans la nature, il existe un processus miroir qui peut également se produire (Fig.2, ci-dessous).

Mais il s'avère que les processus de base de la nature ne sont pas symétriques en P!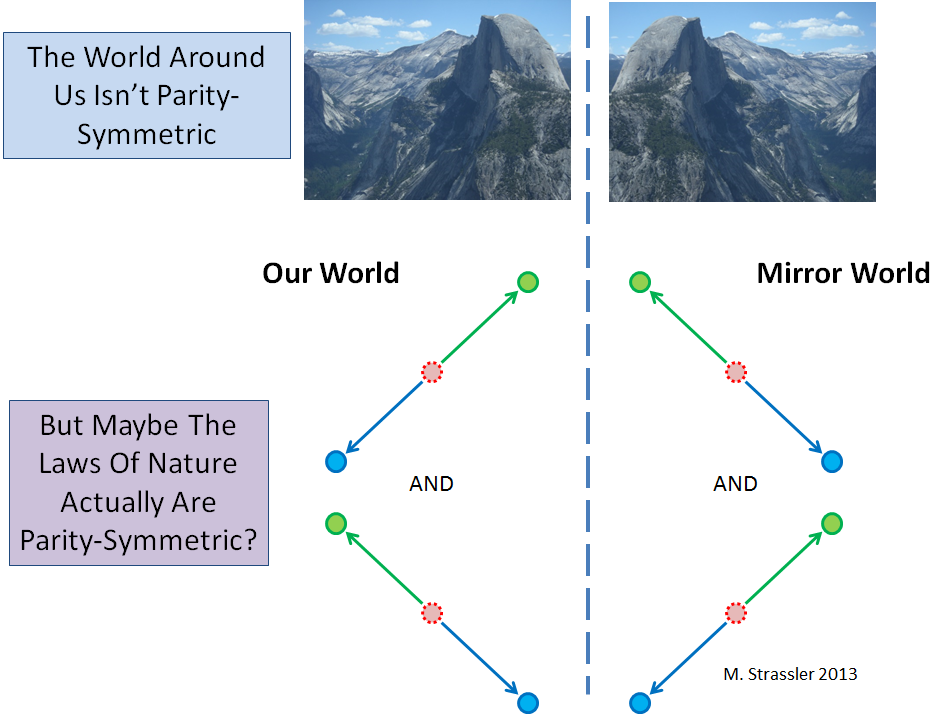


Fig. 2

Un fait frappant est que ni C, ni P, ni T, ni CP, ni CT, ni PC ne sont des symétries de la nature. Les principaux processus connus de la physique avant le XXe siècle - en particulier, y compris les interactions gravitationnelles et électromagnétiques, c'est-à-dire tous ceux qui maintiennent la Terre ensemble et maintiennent son orbite autour du Soleil, et ceux qui contrôlent la physique des atomes et des molécules et toute la chimie - sont symétriques dans S, P et T. Les physiciens ont donc été très surpris quand, dans les années 1950 et 1960, ils ont découvert qu'une faible interaction nucléaire brisait toutes ces symétries. La seule transformation qui est encore considérée (pour une bonne raison) symétrique à la nature est CPT.

Notez que si CPT est symétrie, alors les effets de CP et T devraient être les mêmes. Comme il s'agit de symétrie, l'application de la transformation CPT vous ramène au même monde que celui à partir duquel vous êtes parti, mais il est également connu que si vous appliquez la transformation T deux fois, vous reviendrez au même monde à partir duquel vous avez commencé - ce qui signifie que CP doit faire la même chose qui fait T. La même chose est vraie pour les paires CT et P, et pour RT et C.

Le CPT transforme les particules et leurs interactions dans notre monde en antiparticules et leurs interactions dans un monde transformé, et vice versa. Et, puisque dans notre monde, chaque type de particule a une antiparticule (il se trouve que c'est elle-même), et puisque chaque interaction de particules différentes a une anti-interaction avec les antiparticules (pour ainsi dire), on pense que celle-ci est parfaitement symétrique. Plus précisément, pour tout monde dont les particules obéissent à la théorie quantique des champs, aux mathématiques utilisées dans les équations du modèle standard, qui décrit toutes les particules et interactions connues, il peut être prouvé que CPT est symétrie. (Est-ce vrai pour une théorie unificatrice, telle que la théorie des cordes, combinant la théorie quantique de la gravité avec des forces non gravitationnelles, c'est difficile à dire; mais les violations de CPT n'ont pas encore été obtenues dans les expériences).

C et P ne sont pas des symétries dues à une faible interaction nucléaire

Jusqu'aux années 1950, tout ce que les physiciens savaient - toute la chimie et la physique atomique, tous les effets de la gravité et de l'interaction électromagnétique, les ondes lumineuses et les fondements du noyau atomique - correspondaient à un monde symétrique en P. Mais il s'avère que C et P ne sont pas presque des symétries lois de la nature. Ils sont perturbés le plus souvent possible par de faibles interactions nucléaires.


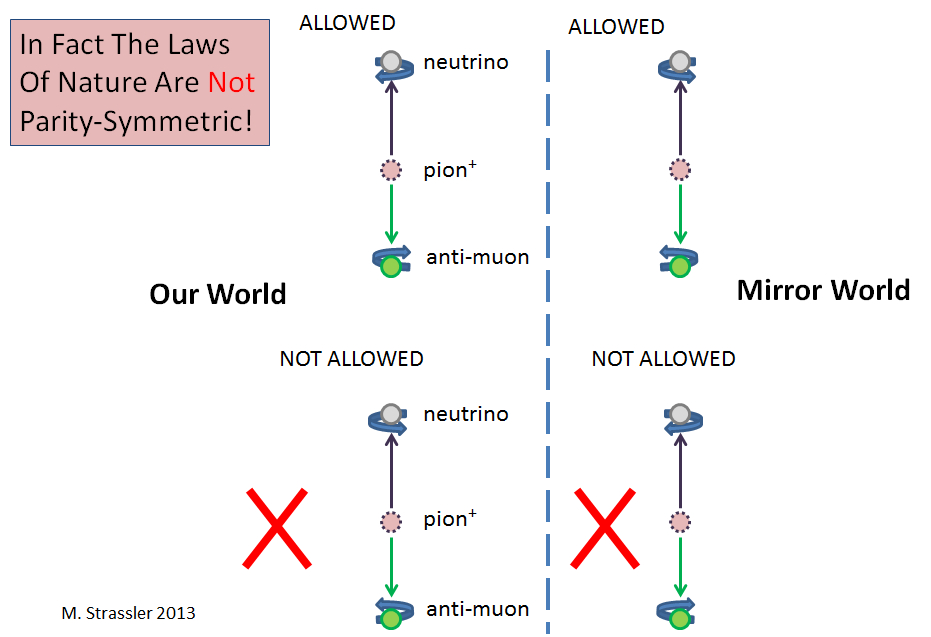Fig. 3

Dans l'exemple le plus simple (mais pas le seul), les neutrinos sont impliqués. Lorsqu'un neutrino apparaît dans un processus physique, il est toujours créé en utilisant une interaction nucléaire faible. Et quand il se produit, il tourne toujours dans le sens antihoraire du point de vue de l'observateur, situé au point d'où il vient. (Les neutrinos, comme les électrons et les protons et de nombreuses autres particules, dans un sens tournent toujours; plus précisément, ils ont toujours un couple). En d'autres termes, il tourne comme une vis pour gaucher (Fig. 3). (Dans le jargon, il aura une hélicité négative). Mais le neutrino produit par la faible interaction nucléaire ne tourne jamais comme une vis pour droitier. Puisque P échangerait les endroits droitiers et gauchers (comme dans un miroir), cela signifie qu'une faible interaction nucléaire viole R.

Dans un exemple plus spécifique (Fig.3), lorsqu'un pion chargé positivement (un hadron composé d'un quark supérieur, d'un quark anti-bas et de nombreux gluons et paires quark / antiquark) se désintègre en un antimuon et un neutrino, le neutrino est toujours gaucher et jamais droitier. Cela viole R. Et lorsqu'un pion chargé négativement se désintègre en un muon et un antineutrino, l'antineutrino est toujours droitier. Cette différence de processus, y compris les pivoines chargées négativement et positivement, viole C.

La violation de P et C de ce type est maintenant tout à fait compréhensible. Le modèle standard (les équations que nous utilisons pour décrire toutes les particules et interactions connues) l'inclut d'une manière assez naturelle, et les détails des équations ont été soigneusement vérifiés lors d'expériences. Ainsi, bien que les violations de P et C aient été une énorme surprise dans les années 1950, elles font aujourd'hui partie intégrante de la physique des particules.

Cependant, si nous regardons les particules elles-mêmes (et n'entrons pas dans les détails de leurs interactions), SR (le même que RS) à première vue semble symétrique. En effet, P fait tourner le spin du neutrino de gauche à droite, mais C inverse la charge du pion, transforme l'antimuon en muon et remplace le neutrino par un antineutrino; le processus final se déroule dans notre monde (Fig. 4). Ainsi, pendant un certain temps, les physiciens ont cru qu'une faible interaction nucléaire préserverait la SR, bien qu'individuellement, elle viole C et R.

Une autre façon de voir cela est de lire mon article sur l'apparence des particules si le champ Higgs était nul. On peut voir que, par exemple, les particules électron-gauche et neutrino-gauche sont appariées et sont sujettes à l'action d'une faible interaction isospin, et la particule électron-droite est séparée de la neutrino-droite, et aucune d'entre elles n'est soumise à une faible interaction isospin. De plus, ce qui est vrai pour la particule électron-droite est également vrai pour la particule positron-droite, et ce qui est vrai pour la particule positron-droite est vrai pour l'électron-gauche. Mais P change les particules électron-gauche et électron-droite, donc évidemment ce n'est pas de la symétrie; C change l'électron gauche et le positron gauche, et comme la particule gauche du positron n'est pas affectée par l'interaction faible, C n'est pas non plus une symétrie. Cependant, CP modifie les particules électron-gauche et positron-droit, et toutes deux sont sujettes à une faible interaction nucléaire.


Fig. 4

CP n'est pas non plus la symétrie

Mais dans les années 1960, il s'est avéré que la RS est également perturbée par une faible interaction nucléaire. Cela a encore une fois été une surprise, compréhensible aujourd'hui, mais toujours en cours d'exploration par nous. Voici une petite histoire.

La plupart des hadrons (particules composées de quarks, d'antiquarks et de gluons) se désintègrent presque instantanément par une forte interaction nucléaire, pendant des temps inférieurs à un billionième de billion de seconde. Un hadron, le proton, est stable; le neutron lui-même vit 15 minutes. (Les noyaux atomiques constitués de protons et de neutrons sont aussi souvent appelés hadrons, mais personnellement, je préfère les appeler "ensembles de hadrons"). Mais pour plusieurs hadrons d'importance historique et pratique, la durée de vie, bien que petite, n'est pas très bonne - quelque part entre un milliardième de milliardième de seconde et un milliardième de seconde - et la plupart d'entre eux se désintègrent en raison d'une faible interaction nucléaire (autres décroissance par interaction électromagnétique). Et dans certains d'entre eux - en particulier les mésons contenant un quark inférieur ou un antiquark inférieur - les désintégrations violant SR ont été mesurées. D'autres signes de violation de CP se trouvent dans les oscillations entre deux hadrons, similaires aux oscillations des neutrinos.

Ce type de violation de CP est très intéressant car il se produit naturellement là où il y a trois ou plusieurs arômes ou générations de quarks supérieurs (supérieurs, charmés et vrais) et trois arômes de quarks inférieurs (inférieurs, étranges et charmants). Comme Kobayashi et Maskawa l'ont souligné, dans une version du modèle standard ne contenant que deux générations, il ne pouvait pas y avoir une telle violation de la RS; il devrait avoir une raison complètement différente. Puisqu'ils ont observé cela bien avant la découverte de la troisième génération de particules, ils ont en fait prédit la nécessité de l'existence de la troisième génération, pour laquelle ils ont par la suite reçu le prix Nobel de physique en 2008 (avec Nambu pour son excellent travail dans d'autres domaines).

Jusqu'à présent, il n'y a aucun signe de violation du CP de nature différente de celle de Kobayashi et Maskawa. Mais s'il y a des particules et des interactions autres que celles qui nous sont connues par le modèle standard, il peut y avoir d'autres conditions où CP est violé.

Cependant, même à l'intérieur du modèle standard, il y a un gros mystère.

Forte interaction nucléaire et SR

Il est très inattendu que SR ne soit pas perturbé de manière significative par une forte interaction nucléaire, et personne ne sait pourquoi il en est ainsi. Nous savons qu'une forte interaction ne viole pas beaucoup le super-réseau en raison d'une certaine propriété du neutron, connue sous le nom de moment dipolaire électrique .

Un neutron est un hadron électriquement neutre très similaire à un proton. Les quarks, antiquarks et gluons qui composent le neutron sont maintenus ensemble par une forte interaction nucléaire. Une question intéressante peut être posée à propos de tout moment électriquement neutre - a-t-il un dipôle électrique.

L'aimant avec lequel vous jouiez quand vous étiez enfant est un dipôle magnétique qui a un pôle nord et sud (Fig. 5). Un monopôle magnétique serait le pôle nord ou sud; mais vous n'avez jamais vu cela, et personne n'a vu. Un dipôle électrique a une charge électrique nulle, mais d'une part, il a des charges positives et, d'autre part, des charges négatives. Cela peut être un cas aussi simple qu'un atome d'hydrogène, avec un électron dans le rôle d'une charge négative et un proton dans le rôle d'une charge positive.

Pour un dipôle électrique simple, composé de deux charges séparées par une distance D, dont l'une a une charge q, et l'autre -q, le moment du dipôle électrique est simplement défini comme q × D.Notez que si la charge positive et négative se trouve au même endroit, alors un tel objet n'a pas de moment dipolaire; les charges doivent être séparées dans l'espace pour qu'il «se polarise». L'atome d'hydrogène n'est généralement pas polarisé. Mais de nombreuses molécules ont un moment dipolaire, bien qu'elles soient électriquement neutres. Par exemple, une molécule d'eau H ₂ O a un moment dipolaire de 3,9 × 10 ^-8 e cm, où "e" est la charge de protons (e est la charge d'électrons) et cm est de 1 centimètre. A titre de comparaison, ce n'est que légèrement inférieur à ce qui peut être obtenu en diluant l'électron et le proton à une distance approximativement égale à la taille de la molécule d'eau (pour un tel dipôle le moment dipolaire serait de l'ordre de 9 × 10 ^-8 e cm). Cela suggère que les électrons de deux atomes d'hydrogène dans H ₂ O passent beaucoup de temps avec l'atome d'oxygène.


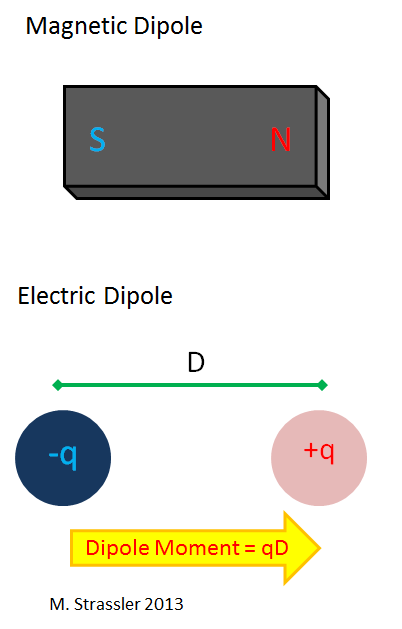Fig. 5

Quelle est la taille du moment dipolaire neutronique? Le rayon des neutrons est de l'ordre de 10 à ¹³ cm, donc on pourrait s'attendre à ce que D soit approximativement le même. Et il se compose de quarks, d'antiquarks et de gluons; les gluons sont électriquement neutres, mais les quarks et antiquarks ont des charges électriques: 2/3 e (quark supérieur), –1/3 e (quark inférieur), –2/3 e (antiquark supérieur) et +1/3 e (antiquark inférieur ) On pourrait donc s'attendre à ce que q soit quelque chose comme ça. Il s'avère que l'on pourrait s'attendre à ce que la magnitude du moment dipolaire électrique du neutron soit ^{comprise entre} 10 et ¹³ e cm. C'est un million de fois plus petit que le moment dipolaire d'une molécule d'eau, principalement parce que le rayon neutronique est inférieur à un million de fois.

En fait, certains effets non évidents nous donnent une estimation d'une taille encore plus petite. L'attente réelle est de l'ordre de 10 ^-15 e cm.

Mais si le neutron a un moment dipolaire électrique, cela violerait T, et donc CP, si CPT peut être considéré comme une symétrie au moins approximative (cela viole également P). Donc, si CP et CPT étaient des symétries exactes, alors le dipôle de neutrons électriques devrait être nul.

Bien sûr, nous savons déjà que CP n'est pas une symétrie exacte; il est rompu par une faible interaction nucléaire. Mais l'interaction faible est si faible (au moins en ce qui concerne les neutrons) qu'elle peut conférer au neutron un moment dipolaire électronique de l'ordre de 10 ^-32 e cm. C'est beaucoup moins que ce que nous pouvons mesurer! Donc, pour nos besoins, il peut être considéré comme nul.

Mais si l'interaction forte qui maintient le neutron ensemble viole le super-réseau, alors nous nous attendons à ce que la magnitude du moment dipolaire électrique soit de 10 ^-15 e cm. Cependant, l'expérience montre que le moment dipolaire électrique du neutron est inférieur à 3 × 10 ^-26 e cm! C'est dix mille millions de fois moins que prévu. Par conséquent, une forte interaction nucléaire ne viole pas le super-réseau aussi fortement que prévu.

Pourquoi est-ce moins que prévu? Personne ne le sait, bien qu'il y ait eu de nombreuses hypothèses. Cette énigme est appelée le problème du CP fort et est l'un des trois plus grands problèmes qui affligent la physique des particules, avec le problème de la hiérarchie et le problème constant cosmologique .

Plus précisément, le problème est le suivant. Si vous écrivez la théorie de l'interaction nucléaire forte - les équations pour les gluons, les quarks et les antiquarks, appelées QCD - alors ces équations auront différents paramètres, à savoir:

• La force unificatrice d'une forte interaction nucléaire,
• masses de quarks différents,
• l'angle thêta, qui n'affecte pas les diagrammes de Feynman, mais détermine néanmoins les effets de divers processus subtils (tunnel quantique, instantons , pseudoparticules) de la physique des gluons.

Arrête quoi? Quel est ce dernier article? Eh bien, ce paramètre facultatif QCD a été découvert dans les années 1970 (c'est l'un des domaines dans lesquels Alexander Polyakov , qui a récemment remporté le prix, est devenu célèbre). Le problème lui-même est de nature trop technique pour être décrit ici, mais il suffit de dire que si l'angle thêta n'est pas égal à 0 ou π, une forte interaction nucléaire viole le super-réseau. Plus précisément, CP viole une certaine combinaison d'angle thêta et de masses de divers quarks (en particulier, le produit des phases complexes de leurs masses). Et ces deux paramètres (angle thêta et masses des quarks) n'ont pas de lien évident - alors comment se combinent-ils pour être parfaitement compensés? Cependant, pour une raison quelconque, leur combinaison est nulle, ou au moins dix milliards de fois plus petite qu'elle ne pourrait l'être. Il n'y a aucune raison évidente à cela.

Les explications suivantes peuvent être données à cette énigme de près de 40 ans:

• le quark supérieur peut ne pas avoir de masse (c'est très difficile à vérifier car il ne peut pas être mesuré directement; les méthodes indirectes disent depuis longtemps que sa masse est plusieurs fois la masse d'un électron, mais certaines subtilités ne nous permettent pas d'interpréter ces méthodes en toute certitude).
• Il y a peut-être un champ d'axion qui supprime cet effet; cette idée prédit l'existence d'une particule d'axion, recherchée depuis plus de 30 ans, mais non encore trouvée.Soit dit en passant, Axion pourrait également jouer le rôle de la matière noire de l'Univers.

Il existe quelques autres solutions possibles à ce problème, mais je ne les décrirai pas ici; malheureusement, en général, elles n'ont pas de conséquences expérimentales évidentes qui pourraient être vérifiées dans un avenir proche.