
La théorie de la relativité fascine par ses paradoxes. Nous connaissons tous les jumeaux, la possibilité de mettre un long avion dans une petite boîte. Aujourd'hui, chaque diplômé de l'école connaît les réponses à ces énigmes classiques, et les étudiants en physique croient encore plus qu'il n'y a pas de secret pour eux dans la théorie spéciale de la relativité.
Tout irait bien sans une situation déprimante - l'impossibilité de vitesses supraluminiques. Y a-t-il vraiment aucun moyen plus rapide? - J'ai pensé dans l'enfance. Ou peut-être le pouvez-vous?! Je vous invite donc à une séance, je ne sais pas, de magie noire ou blanche du nom d'Albert Einstein avec une exposition à la fin. Cependant, pour ceux qui semblent un peu, j'ai également préparé une tâche.
UPD: Un jour plus tard, je publie la décision. Beaucoup de formules de texte, des graphiques à la fin.
À Alpha Centauri
Je vous invite à prendre place dans notre vaisseau interstellaire, qui se dirige vers Alpha Centauri. Du point final de l'itinéraire, nous sommes éloignés de 4 années-lumière. Attention, démarrez les moteurs. C'est parti! Pour le confort des passagers, notre capitaine a défini une telle poussée pour accélérer avec une valeur

et senti la force de gravité qui nous est familière sur Terre.
Maintenant, nous avons décemment accéléré, même si la moitié de la vitesse de la lumière

. Posons une question simple: à quelle vitesse aborderons-nous Alpha Centauri dans notre propre référentiel (navire). Cela semblerait simple si nous volons à une vitesse

dans le référentiel fixe de la Terre et des Alpha Centauri, puis de notre point de vue nous approchons de la cible avec rapidité

.
Quiconque a déjà ressenti le problème a tout à fait raison. La réponse

mal! Ici, nous devons clarifier, sous la vitesse d'approche d'Alpha Centauri, j'appelle le changement de la distance restante à celui-ci, divisé par la période de temps pendant laquelle un tel changement s'est produit. Tout, bien sûr, est mesuré dans notre référentiel associé à l'engin spatial.
Il faut rappeler ici la réduction lorentzienne de la longueur. Après avoir accéléré à la moitié de la vitesse de la lumière, nous constatons que l'échelle le long de la direction de notre mouvement s'est contractée. Permettez-moi de vous rappeler la formule:
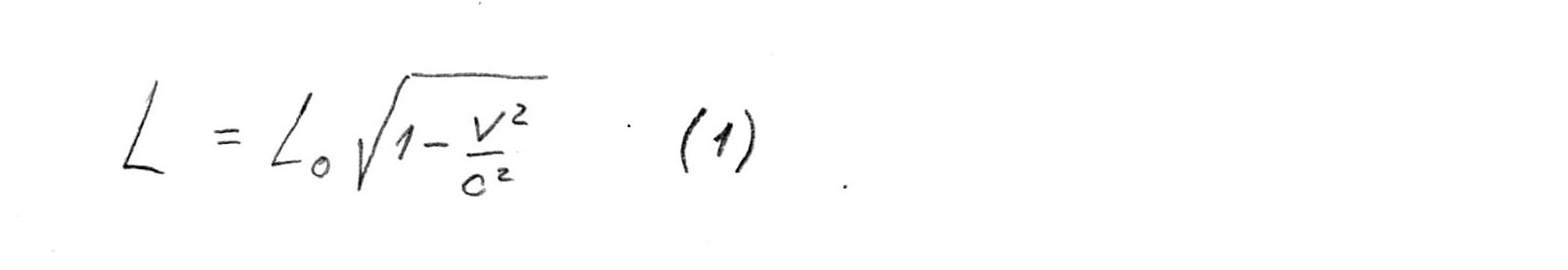
Et maintenant, si à une vitesse de la moitié de la vitesse de la lumière, nous mesurons la distance de la Terre à Alpha Centauri, nous n'avons pas obtenu 4 St. ans, et seulement 3,46 St.
Il s'avère que ce n'est que grâce au fait que nous avons accéléré

nous avons déjà réduit la distance jusqu'à la destination finale du voyage de près de 0,54 St. Et si nous nous déplaçons non seulement à grande vitesse, mais aussi en accélérant, le facteur d'échelle aura une dérivée temporelle, qui a également essentiellement une vitesse d'approche et est plus

.
Ainsi, en plus de notre habitude, je dirais classique, la vitesse

un autre terme est ajouté - une réduction dynamique de la longueur du chemin restant, qui se produit si et seulement s'il y a une accélération non nulle. Eh bien, prenez un crayon et comptez.
Et ceux qui sont trop paresseux pour suivre les calculs que je rencontre de l'autre côté du spoiler
- la distance actuelle à l'étoile dans la ligne du capitaine du navire,

- le temps de quart dans la salle de garde,

- la vitesse.

Déjà ici, nous voyons que la première dérivée partielle est la vitesse, juste la vitesse

avec un signe moins, puisque nous approchons d'Alpha Centauri. Mais le deuxième terme est la prise même, à laquelle, je suppose, tout le monde n'a pas pensé.
Pour trouver la dérivée temporelle de la vitesse au second terme, il faut être prudent, car nous sommes dans un référentiel mouvant. Il est plus facile de calculer sur les doigts à partir de la formule pour ajouter des vitesses relativistes. Laissez à la fois

on avance à une vitesse

, et après un certain temps, notre vitesse a augmenté de

. La vitesse résultante selon la formule de la théorie de la relativité sera

Maintenant, nous collectons ensemble (2) et (3), et la dérivée de (3) doit être prise pour

parce que nous envisageons de petits incréments.
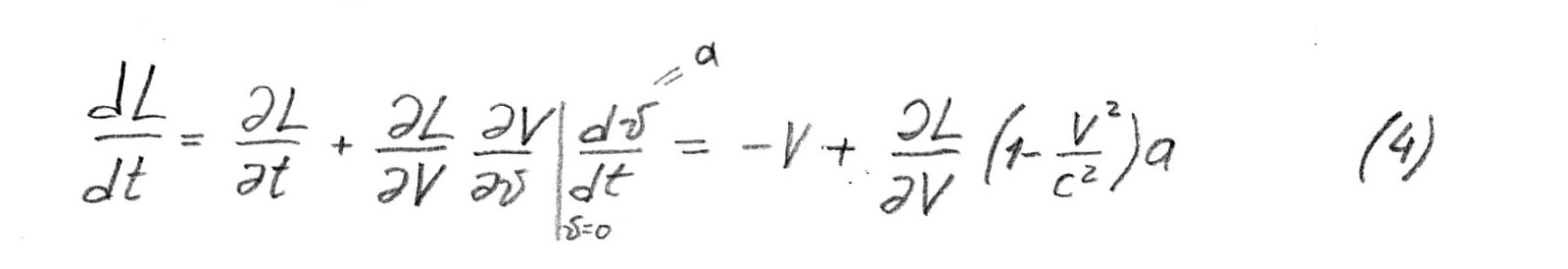
Admirons la formule finale
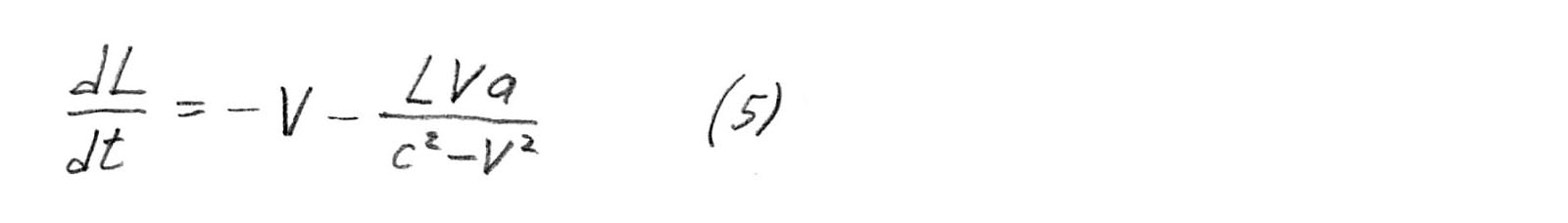
Elle est incroyable! Si le premier terme - la vitesse - est limité par la vitesse de la lumière, alors le second terme n'est limité par rien! Prenez

plus grand et ... le deuxième terme peut facilement dépasser

.
- Quoi, quoi! - certains ne croiront pas.
«Oui, oui, exactement ainsi», je répondrai. - Cela peut être plus que la vitesse de la lumière, plus de deux vitesses de lumière, plus de 10 vitesses de lumière. Pour paraphraser Archimède, je peux dire: «donne-moi le droit

, et je vous fournirai une vitesse arbitrairement élevée. "
Eh bien, substituons les nombres, avec des nombres toujours intéressants. Comme nous nous en souvenons, le capitaine a réglé l'accélération

, et la vitesse a déjà atteint

. Ensuite, nous constatons que pour

année-lumière, notre vitesse d'approche est égale à la vitesse de la lumière. Si nous substituons

années-lumière alors

J'écris: "trois entiers, trois dixièmes de la vitesse de la lumière."
Continuez à vous demander
Examinons de plus près la formule (5). Après tout, il n'est pas nécessaire de monter à bord d'un vaisseau spatial relativiste. La vitesse et l'accélération peuvent être très faibles. Tout tourne autour de la magie

. Pensez-y!
Je suis donc monté dans la voiture et j'ai pressé le gaz. J'ai de la vitesse et de l'accélération. Et en ce moment même, je peux garantir qu'à quelque cent ou deux millions d'années-lumière devant moi, il y a des objets qui m'approchent maintenant plus vite que la lumière. Par souci de simplicité, je n'ai pas encore pris en compte la vitesse de la Terre sur son orbite autour du Soleil, et du Soleil autour du centre de la Galaxie. Avec leur tolérance, les objets avec une vitesse d'approche supraluminique seront déjà assez proches - pas à l'échelle cosmologique, mais quelque part à la périphérie de notre Galaxie.
Il s'avère que involontairement, même avec une accélération minimale, par exemple, en se levant d'une chaise, nous participons au mouvement supraluminique.
Nous sommes encore surpris
Regardez la formule (5) de très très près. Voyons non pas la vitesse d'approche d'Alpha Centauri, mais plutôt la vitesse de distance de la Terre. Avec un assez gros

par exemple, à mi-chemin de l'objectif, nous pouvons constater que la Terre et l'Alpha Centauri s'approchent de nous. Après avoir récupéré de la surprise, bien sûr, vous pouvez deviner que la faute est le raccourcissement de la longueur, qui fonctionne non seulement en avant, mais aussi en arrière. L'espace derrière la poupe du vaisseau spatial rétrécit plus vite que nous ne nous éloignons du point de départ.
Il est facile de comprendre un autre effet étonnant. Après tout, il vaut la peine de changer le sens de l'accélération, car le deuxième terme de (5) change immédiatement de signe. C'est-à-dire la vitesse d'approche peut facilement devenir nulle, voire négative. Bien que la vitesse habituelle

nous continuerons d'être dirigés vers Alpha Centauri.
Exposition
J'espère que je vous ai suffisamment dérouté. Comment cela, on nous a appris que la vitesse de la lumière est maximale! Vous ne pouvez pas approcher quoi que ce soit plus vite que la vitesse de la lumière! Mais ici, il convient de prêter attention au dicton de toute loi relativiste. C'est dans n'importe quel manuel, mais il semble que cela n'encombre que le libellé, même si c'est en lui que réside tout le «sel». Ce dicton dit que les postulats de la théorie spéciale de la relativité fonctionnent "dans un référentiel inertiel".
Dans un référentiel non inertiel, Einstein ne nous garantit rien. De telles choses!
La même chose, un peu plus détaillée et un peu plus compliquéeLa formule (5) contient la distance

. Quand il est nul, c'est-à-dire lorsque nous essayons de déterminer la vitesse d'objets localement relativement proches, seul le premier terme reste

, qui, bien sûr, ne dépasse pas la vitesse de la lumière. Pas de problème. Et seulement à de grandes distances, c'est-à-dire pas localement, nous pouvons obtenir des vitesses ultra-légères.
Je dois dire que, d'une manière générale, la vitesse relative des objets éloignés les uns des autres est un concept mal défini. Notre espace-temps plat dans un cadre de référence accéléré semble incurvé. Il s'agit du fameux "ascenseur Einstein" équivalent au champ gravitationnel. Et il est correct de comparer deux quantités vectorielles dans un espace courbe uniquement lorsqu'elles sont au même point (dans un espace tangent du faisceau vectoriel correspondant).
En parlant de notre paradoxe de la vitesse supraluminique, on peut raisonner différemment, je dirais intégralement. Après tout, un voyage relativiste à Alpha Centauri prendra les propres heures du cosmonaute beaucoup moins de 4 ans, donc en divisant la distance d'origine par le temps passé seul, nous obtiendrons une vitesse effective supérieure à la vitesse de la lumière. En fait, c'est le même double paradoxe. Pour qui cela convient, c'est exactement ainsi que le mouvement ultra-léger peut être compris.
Voilà toute l'astuce. Votre Captain Evidence.
Et enfin, je suis venu avec vos devoirs
ou ébauche pour discussion dans les commentaires .
Tâche
Les terriens et les alpha-centaures ont décidé d'échanger des délégations. Un vaisseau spatial lancé à partir de la Terre à une vitesse

. Dans le même temps, une soucoupe volante d'extraterrestres à la même vitesse partit d'Alpha Centauri.

Quelle est la distance entre les navires dans le cadre de référence du navire des terriens au moment du lancement, lorsqu'ils étaient près de la Terre et d'Alpha Centauri, respectivement? Écrivez votre réponse dans les commentaires.
UPD: Solution
Donc, la solution au problème. Tout d'abord, considérez-le qualitativement.
Nous convenons que les horloges sur Alpha, Terre, la fusée et la plaque sont synchronisées (cela a été fait à l'avance), et le départ pour les quatre heures a eu lieu à 12h00.
Considérez l'espace-temps graphiquement en coordonnées de repos

. La Terre est à zéro, alpha au loin

le long de l'axe

. La ligne mondiale d'Alpha Centauri monte évidemment juste verticalement. La ligne mondiale de la plaque va avec une pente vers la gauche, car elle a volé hors de propos

en direction de la terre.
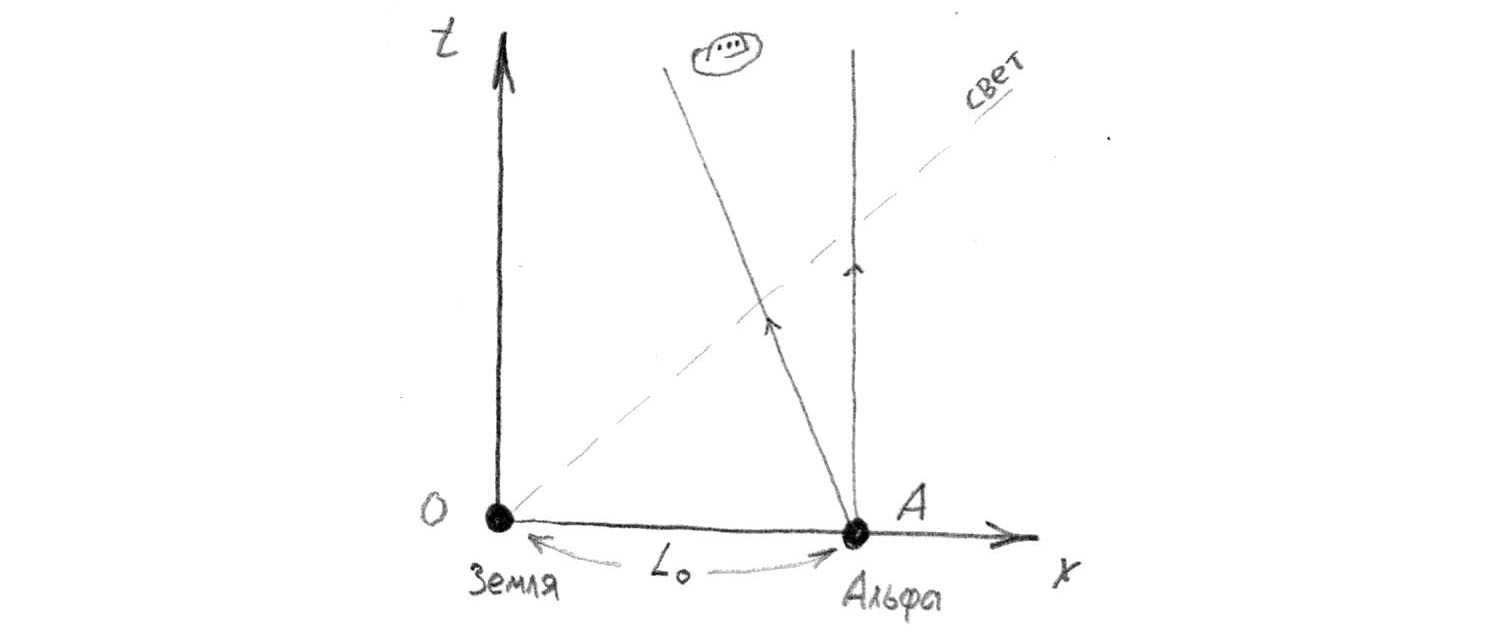
Maintenant, sur ce graphique, nous allons dessiner les axes de coordonnées du référentiel de la fusée lancée depuis la Terre. Comme vous le savez, une telle transformation du système de coordonnées (SC) est appelée un boost. Dans ce cas, les axes sont inclinés symétriquement par rapport à la ligne diagonale, qui montre le faisceau lumineux.
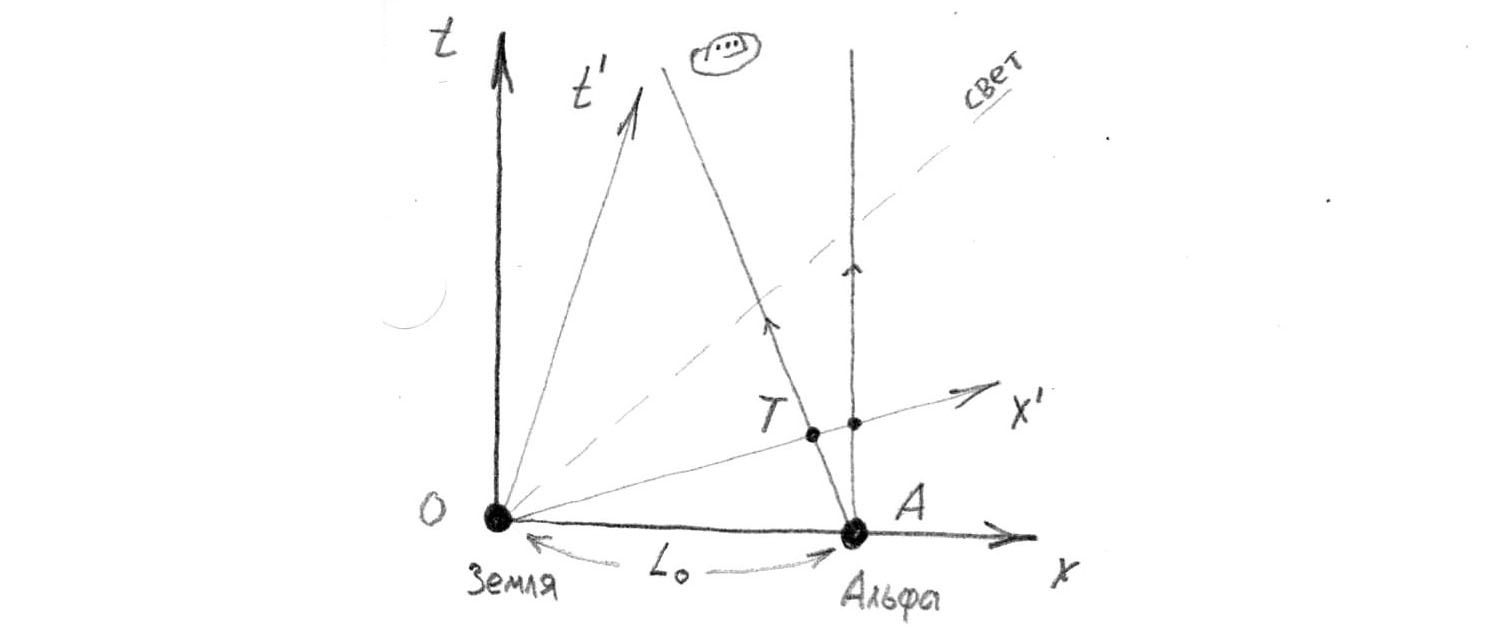
Je pense qu'à ce moment tout est devenu clair pour vous. Regarder l'axe

traverse les lignes mondiales d'Alpha et de la soucoupe volante à différents points. Que s'est-il passé?
La chose incroyable. Du point de vue de la fusée, la plaque et l'Alpha étaient au même point avant le départ, et après accélération, il s'avère que dans le SC en mouvement, le lancement de la fusée et de la plaque n'a pas été simultané. L'assiette, il s'avère soudain, a commencé plus tôt et a réussi à se rapprocher un peu de nous. Par conséquent, à 12:00:01, l'horloge du missile est plus proche de la plaque que d'Alpha.
Et si la fusée accélère à nouveau, elle "sautera" dans la prochaine SK, où la plaque est encore plus proche. De plus, une telle approximation de plaque ne se produit que du fait de l'accélération et de la compression dynamique de l'échelle longitudinale (ce qui est tout mon sujet), et non de l'avance de la fusée dans l'espace, car la fusée n'avait toujours pas eu le temps de voler. Cette approximation de plaque est précisément le deuxième terme de la formule (5).
Eh bien, en plus de tout le reste, il faut tenir compte de la réduction de distance habituelle de Lorentz. Je vous informerai immédiatement qu'à des vitesses de fusée et de cymbale

chaque distance
- entre la fusée et Alpha: 3,46 St. ans (réduction conventionnelle de Lorentz)
- entre la fusée et la plaque: 2,76 St. de l'année
Peu importe, épelons avec des formules dans un espace à quatre dimensionsIl est commode de résoudre de tels problèmes à l'aide de vecteurs à quatre dimensions. Ils n'ont pas besoin d'avoir peur, tout se fait en utilisant les actions les plus courantes de l'algèbre linéaire. De plus, nous ne nous déplaçons que le long d'un axe, il ne reste donc que deux coordonnées des quatre coordonnées:

et

.
Ensuite, nous sommes d'accord sur une notation simple. La vitesse de la lumière est considérée comme égale à l'unité. Nous, physiciens, faisons toujours cela. :) Nous considérons également généralement l'unité comme la constante de Planck et la constante gravitationnelle. Cela ne change pas l'essence, mais facilite énormément l'écriture.
Ainsi, la «racine relativiste» omniprésente est désignée par le facteur gamma pour la compacité des enregistrements, où

- Vitesse de la fusée terrestre:

Maintenant, nous écrivons le vecteur dans les composants

:

La composante supérieure est le temps, la composante inférieure est la coordonnée spatiale. Les navires démarrent simultanément dans un système fixe, de sorte que la composante supérieure du vecteur est zéro.
Trouvez maintenant les coordonnées du point

dans un système de coordonnées en mouvement

, c'est-à-dire

. Pour ce faire, nous utilisons la transformation en référentiel mobile. Cela s'appelle boost et se fait très simplement. Tout vecteur doit être multiplié par la matrice de boost

Multipliez:
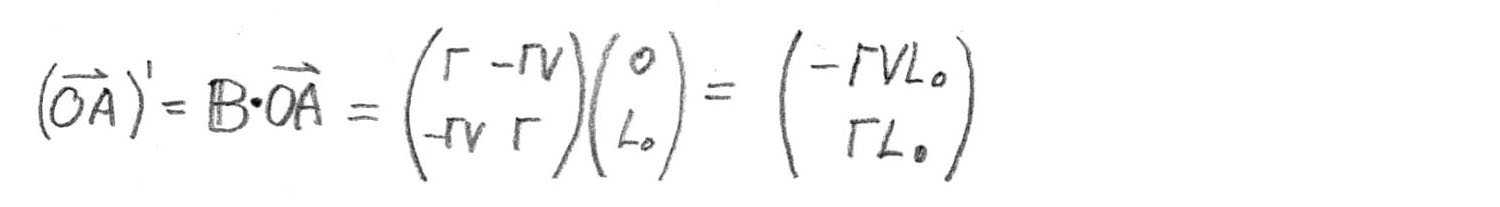
Comme nous le voyons, la composante temporelle de ce vecteur est négative. Cela signifie également que le point

en termes de fusée en mouvement est sous l'axe

, c'est-à-dire dans le passé (comme le montre la figure ci-dessus).
Trouvez le vecteur

dans un système fixe. Composante temporelle - une période de temps inconnue

spatial - la distance que la plaque approche dans le temps

se déplacer à grande vitesse

:

Maintenant, le même vecteur dans le système

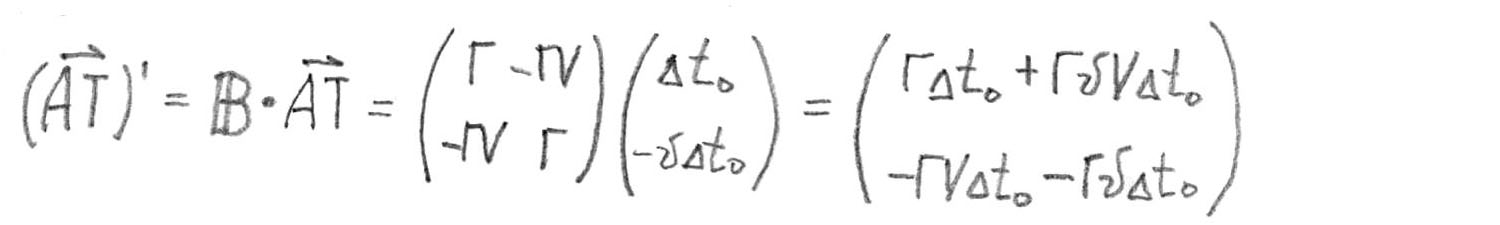
Trouver la somme vectorielle habituelle

Pourquoi ai-je assimilé ce montant à droite à un tel vecteur? Par définition, le point

est sur l'axe

donc la composante temporaire

devrait être égal à zéro, et la composante spatiale - ce sera la même distance souhaitée

d'une fusée à une plaque. De là, nous obtenons un système de deux équations simples - nous égalisons les composantes temporelles séparément, les composantes spatiales séparément.
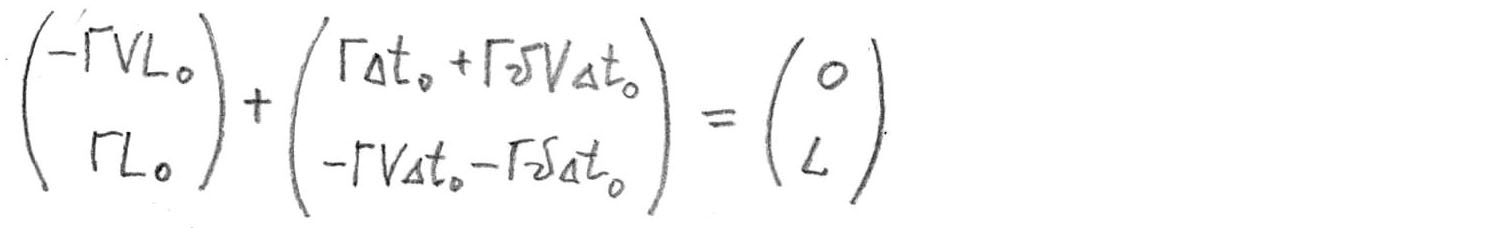
À partir de la première équation, nous déterminons le paramètre inconnu

, remplacez-le dans la deuxième équation et obtenez

. Oublions les calculs simples et notons immédiatement

Substitution

,

nous obtenons
