Dans cet article, je vais vous dire quelque chose sur le fonctionnement de la mécanique quantique, en particulier, sur le phénomène étonnant appelé «fluctuations quantiques», et comment il est utilisé dans la théorie des champs quantiques, dont un exemple est le modèle standard (les équations que nous utilisons pour prédire le comportement des particules élémentaires connues et des interactions). Une compréhension profonde de ce phénomène et de l'énergie qui y est associée nous conduit directement à l'un des conflits les plus graves et non résolus de la science: le problème de la constante cosmologique. Elle nous conduit également au mystère du naturel ou au
problème de la hiérarchie .
Dans la théorie quantique des champs, les fluctuations quantiques sont parfois appelées ou décrites comme «l'apparition et la disparition de deux ou plusieurs particules virtuelles». Ce jargon technique est très infructueux, car ces choses (quoi que nous les appelions) ne sont certainement pas des particules - par exemple, elles n'ont pas une certaine masse - et aussi, puisque le concept de «particule virtuelle» n'est précisément défini qu'en présence d'interactions relativement faibles .
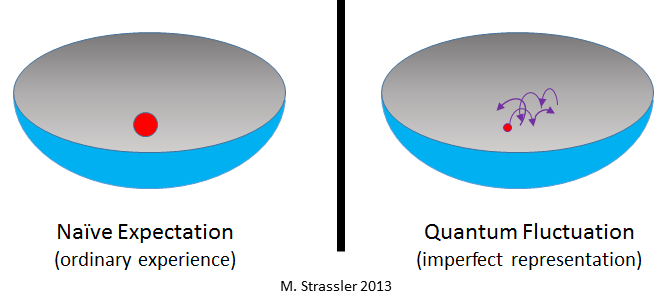Fig. 1Les fluctuations quantiques sont étroitement liées au principe d'incertitude de Heisenberg. Voici un exemple classique et simple (Fig. 1). Si vous placez la balle au fond du bol, elle y restera indéfiniment seule. Cela peut être attendu de l'expérience quotidienne. Et en l'absence de mécanique quantique, ce serait le cas. Mais si vous mettez une particule très légère dans un petit bol ou un autre type de piège, vous constaterez qu'elle ne repose pas au fond. Si elle était immobile ci-dessous, elle violerait le principe d'incertitude - garantissant que vous ne pouvez pas simultanément savoir exactement où se trouve la particule (c'est-à-dire en bas) et comment elle se déplace (dans notre cas, ce n'est pas le cas). Cela peut être imaginé, bien qu'imparfaitement, mais pratique, comme une sorte de tremblement constant qui affecte la particule et ne lui permet pas de se calmer, comme l'indique l'intuition sur l'exemple des boules et des bols. Un aspect utile de cette image imparfaite est qu'elle montre clairement que l'énergie peut être associée à ce tremblement.
Dans la théorie des champs quantiques - équations quantiques pour des champs tels que l'électricité, un effet similaire est observé. Permettez-moi de l'expliquer.
Fluctuations du champ quantique
Chaque particule élémentaire (et je parle de vraies particules) dans notre Univers est une ondulation, une petite onde, une onde de la plus faible intensité possible, voyageant le long du champ quantique élémentaire correspondant (Fig.2). La particule W est une onde dans le champ W; photon - une onde dans un champ électrique; quark supérieur - une onde dans le champ du quark supérieur.
Et s'il n'y a pas de particules? Même là où, à notre avis, il n'y a que de l'espace vide, les champs existent toujours - il s'assoit tranquillement pour lui-même, tout comme il y a de l'eau dans l'étang, même si ni le vent ni les cailloux ne provoquent des ondulations à sa surface, et comme dans une pièce il y a de l'air même s'il n'y a pas de sons.
Fig. 2Cependant, le fait est que ces champs ne se comportent jamais de manière absolument silencieuse. Les champs quantiques ne prennent pas en charge une valeur constante; leur valeur n'importe où dans l'espace tremble toujours un peu. La gigue est appelée «fluctuations quantiques» et, comme pour une particule dans un petit bol, elle est la conséquence du fameux «principe d'incertitude de Heisenberg». Vous ne pouvez pas connaître la valeur d'un champ et en même temps le modifier; votre connaissance d'une de ces quantités, et généralement de deux, doit être imparfaite. Et ces fluctuations sont parfois aussi expliquées comme la raison de la présence de deux ou plusieurs «particules virtuelles», mais ce nom n'est associé qu'à des aspects techniques (au calcul des propriétés des fluctuations à l'aide des fameux
diagrammes de Feynman ), et ne dit pas comment il faut l'imaginer.
La question évidente est: êtes-vous sûr de la présence de fluctuations de champ quantique? Réponse: oui, bien que pour l'instant je ne l'explique pas. Un exemple: les fluctuations quantiques conduisent au fait que la force des interactions flotte lorsque vous la mesurez à des distances de plus en plus courtes - et nous observons non seulement cet effet, il coïncide également avec une grande précision avec ce que nous pouvons calculer en utilisant Modèle standard. Ce succès confirme non seulement la présence de fluctuations quantiques, mais aussi la structure détaillée du modèle standard, jusqu'à des distances de l'ordre d'un millionième de millionième de millionième de millionième de mètre. Autre exemple: la réaction d'un électron à un champ magnétique peut être mesurée avec une précision d'un billion; il peut également être calculé à l'aide du modèle standard avec une précision d'un billionième, en supposant la présence de fluctuations dans les champs que nous connaissons. Étonnamment, les mesures coïncident avec les calculs du modèle standard.
Ce qui est important, ce tremblement génère une certaine quantité d'énergie - beaucoup. Combien Plus votre microscope (ou accélérateur de particules) est meilleur, plus vous voyez de gigue et plus vous trouvez d'énergie de gigue.
Considérons une boîte avec un bord d'un mètre et demandez: combien d'énergie associée à la gigue d'un champ quantique peut être comptée dans cette boîte (Fig. 3)?
Calcul 1: disons, comme le montrent nos mesures expérimentales au Grand collisionneur de hadrons, le modèle standard - une description pratique de tous les processus se produisant à des distances supérieures à un millionième de millionième de millionième de mètre - appelons cela la «distance TANK» d'environ 1/1000 du rayon du proton , car une telle échelle d'expériences peut être réalisée au LHC - des processus y sont disponibles, y compris des collisions de particules élémentaires avec des énergies inférieures à 1000 énergies de protons de masse (l'énergie que E = mc
2 ). Cette énergie est une énergie de masse typique de la particule la plus lourde, que l'on peut espérer découvrir lors de collisions de protons dans le LHC, appelons-la donc «énergie du LHC». Toda, la quantité d'énergie des fluctuations de chaque champ dans le modèle standard (par exemple, un champ électrique) est la suivante: dans chaque cube avec la taille des bords égale à la distance TANK, l'énergie TANK est contenue. En d'autres termes, la densité d'énergie est d'une énergie du LHC pour un volume du LHC.
Comparez cela à la matière ordinaire, dont la densité d'énergie est égale à plusieurs énergies de masse d'un proton ou d'un neutron (c'est-à-dire les énergies de masse d'un noyau atomique) pour chaque atome, dont le volume, car un proton ou un neutron est 100 000 fois plus petit que le rayon d'un atome, est de 1 000 000 000 000 000 fois le volume de protons. (N'oubliez pas que l'atome est relativement beaucoup plus vide que le système solaire). Cela signifie que la densité d'énergie des fluctuations quantiques du champ électrique est environ un million de millions de millions de fois supérieure à celle de la matière ordinaire, donc l'énergie de la masse des fluctuations du champ électrique avec un bord d'un mètre est environ un million de millions de millions de fois supérieure à l'énergie contenue dans un mètre cube de matière solide. Et combien d'énergie est-ce? De quoi faire exploser une planète entière, voire une étoile! Elle est comparable en magnitude à l'énergie totale du soleil. Bien sûr, cette énergie ne peut pas être libérée du vide, ni pour le mal ni pour le bien, il n'y a donc pas lieu de s'inquiéter - ce n'est pas dangereux. Mais cela suffit pour comprendre l'ampleur du problème de la constante cosmologique.
Calcul 2: disons, en ce qui concerne la question de la hiérarchie et de la naturalité de l'Univers, que le modèle standard décrit tous les processus de la physique des particules jusqu'à l'échelle à laquelle la gravité devient une forte interaction - la soi-disant La longueur de Planck, qui, à son tour, est un autre million de millions de fois inférieure à la distance du calcul 1. La quantité d'énergie des fluctuations du champ électrique contenue dans un mètre cube est alors supérieure à celle du calcul 1
(1 000 000 000 000 000)
4 = 1 avec 60 zéros
fois.
Si vous prenez ce nombre et le multipliez par le nombre de compter 1, vous aurez suffisamment d'énergie pour faire exploser toutes les étoiles de toutes les galaxies dans la partie visible de l'Univers de nombreuses fois. Et juste autant d'énergie est contenue dans chaque mètre cube - si le modèle standard décrit correctement les processus physiques sur des échelles allant jusqu'à la longueur de Planck.
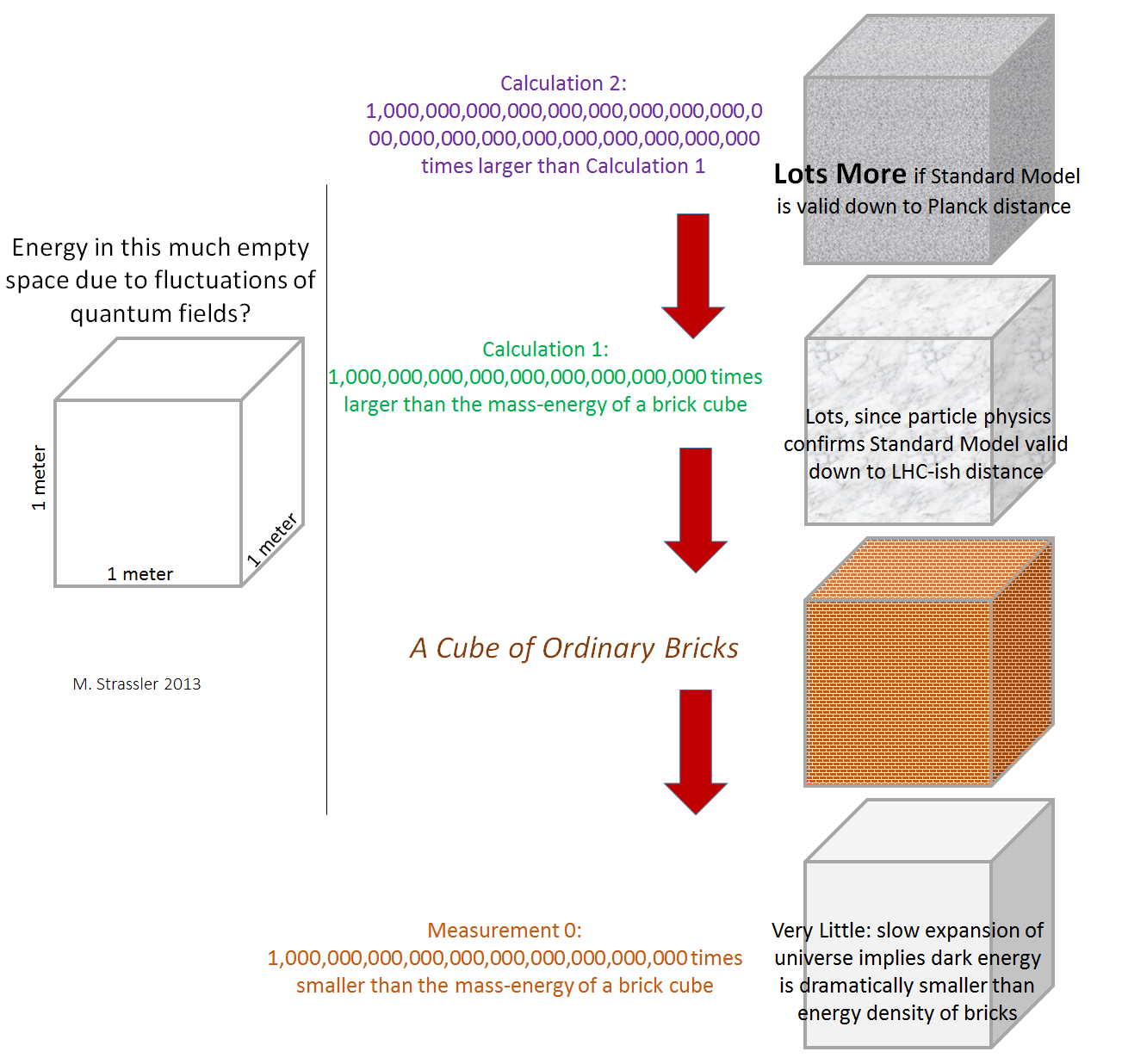Fig. 3En général, si le modèle standard (ou toute théorie de champ quantique typique sans symétries spéciales) est vrai jusqu'aux échelles de longueur L, alors l'énergie de fluctuation dans un cube de taille L
3 est approximativement égale à hc / L pour chaque champ, où h est la constante de Planck et c est limite de vitesse universelle, connue sous le nom de «vitesse de la lumière». Cela signifie que la densité d'énergie est approximativement égale à hc / L
4 - si L diminue de 10 fois, alors la densité d'énergie augmente de 10 000 fois! C'est pourquoi les chiffres dans les calculs 1 et 2 se sont avérés si énormes.
Ces déclarations peuvent vous sembler étranges. Ils sont étranges - mais la physique quantique est pleine de bizarreries. De plus, ni la mécanique quantique ni la théorie quantique des champs n'ont encore échoué. Comme je l'ai mentionné plus tôt, nous avons des preuves complètes que les calculs les plus simples, similaires à ceux présentés, fonctionnent parfaitement dans la théorie quantique des champs. Le fait de l'existence de fluctuations quantiques, ainsi que leur énergie, est si profondément ancré dans la mécanique quantique que pour les déclarer fausses, vous devrez expliquer toute une bibliothèque de résultats expérimentaux par lesquels la mécanique quantique a fait les bonnes prévisions. Ainsi, comme pour les scientifiques, nous n'avons d'autre choix que de prendre ces calculs au sérieux et d'essayer de les comprendre.
Vous pouvez avoir quelques questions évidentes: pourquoi ne pouvons-nous pas simplement déterminer si cette énergie est là ou non? Pourquoi toute cette énorme énergie n'a-t-elle aucun effet sur la matière ordinaire et sur nous-mêmes? La première partie de la réponse: puisque chaque mètre cube d'espace contient la même quantité d'énergie, à l'intérieur et à l'extérieur de n'importe quel cube (Fig.4) que vous pouvez dessiner. Analogie: il y a une pression d'air à l'intérieur de la maison, mais la maison n'explose pas à cause de cela, alors qu'il y a une pression d'air égale à l'extérieur de la maison. De la même manière, le fait que cette énergie de densité de minuscules fluctuations quantiques soit constante dans l'espace et le temps signifie qu'elle n'a aucun effet sur les objets qui s'y reposent ou se déplacent. Seuls les changements d'énergie dans le temps ou dans l'espace agiront sur les particules, sur les atomes constitués de ces particules, sur les personnes et les planètes constituées de ces atomes. En effet, cette énergie de fluctuations quantiques est la même partout et toujours, donc il est impossible de la ressentir, de l'essayer ou de l'utiliser.
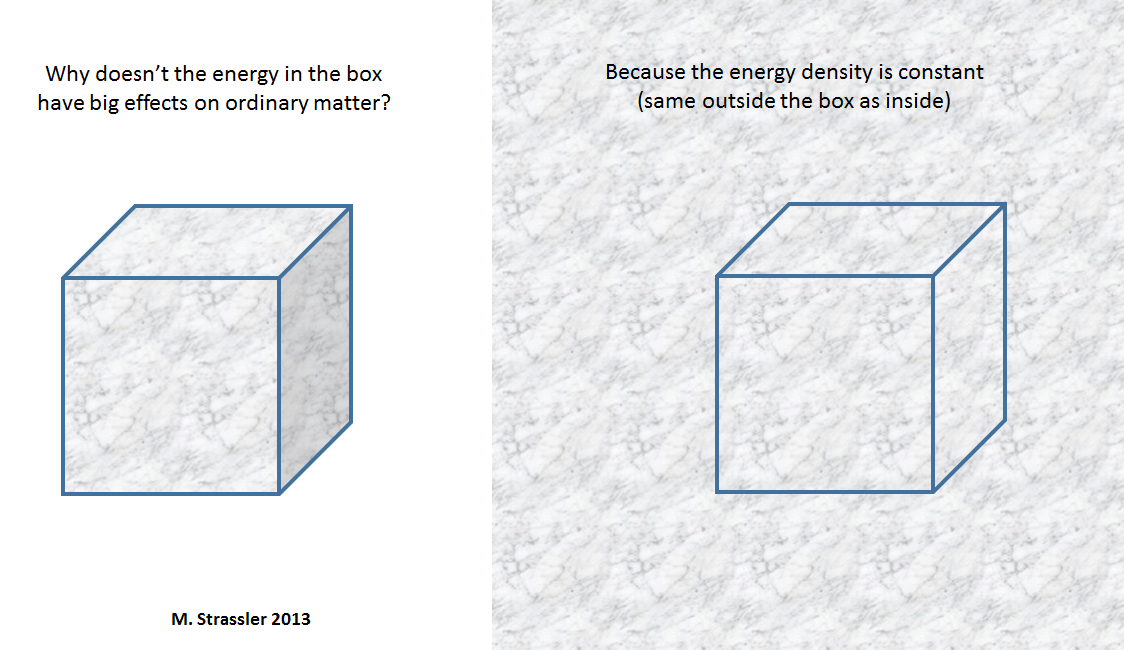Fig. 4Cependant! Réponse, partie 2: bien que dans la gravité newtonienne, dans laquelle la gravité attire les masses, cette énergie de l'espace vide ne se manifestera en aucune façon, dans la version d'Einstein, où la gravité attire l'énergie et l'élan, ce ne sera pas le cas. Que ce soit en comptant 1, ou en comptant 2, ou quelque chose de moyen sera correct, une telle quantité d'énergie dans chaque mètre cube d'espace - ce qui est souvent appelé "énergie sombre" - devrait faire se développer l'Univers à une vitesse énorme! Ce mécanisme a conduit à «l'inflation cosmique», la phase par laquelle l'Univers a pu passer il y a très longtemps, ce qui l'a rendu aussi uniforme que nous le voyons aujourd'hui. Le fait que l'Univers ne se dilate pas à une vitesse énorme suggère que la densité d'énergie de l'espace devrait être bien inférieure à la densité d'énergie de la matière ordinaire, et pas beaucoup plus. Chaque mètre cube d'espace vide ne contient que l'énergie de la masse d'un atome, et le mètre cube de matière solide contient l'énergie de la masse de nombreux atomes - environ 1 avec 30 zéros. Le fait que dans l'espace vide la densité d'énergie soit apparemment très faible, malgré tous nos calculs de combien elle devrait être due aux fluctuations quantiques des champs que nous connaissons, est le père et la mère de tous les grands mystères de la physique quantique: problème constant cosmologique.
La prochaine question évidente: êtes-vous sûr que les fluctuations quantiques ont réellement de l'énergie, ou peut-être qu'elles ne sont pas là, ce qui pourrait éliminer le problème de la constante cosmologique? Réponse: oui, je suis sûr que les fluctuations quantiques ont de l'énergie. On l'appelle énergie nulle, et elle est fondamentale en mécanique quantique, grâce encore une fois au principe d'incertitude. Et cela peut être vérifié: dans une expérience astucieuse, l'énergie peut fonctionner grâce
à l'effet Casimir , qui était prédit dans les années 1940, a été observé pour la première fois dans les années 1970 et testé avec plus de précision dans les années 1990. Cependant, il existe une controverse quant à savoir si elle est réellement liée à notre sujet.
Le problème de la constante cosmologique est très grave. Nous savons expérimentalement que l'Univers ne se développe pas à une vitesse incroyable; elle le fait assez lentement; ce sera la mesure 0 sur la fig. 3 (en bas). Par conséquent:
• Soit ce décompte (et même le décompte 1, qui ne fait aucune hypothèse que nous ne connaissons pas du modèle standard) est en quelque sorte erroné, et cette énergie ne l'est pas,
• Soit l'effet de cette énergie sur l'expansion de l'Univers n'est pas ce que nous pensons, parce que nous comprenons mal la gravité,
• Soit le calcul est correct, mais il répond à la mauvaise question d'une manière que nous ne comprenons pas.
Personne ne sait avec certitude. Je parlerai des solutions possibles à ce problème dans un article séparé sur la constante cosmologique. Mais j'ai mentionné une solution intéressante qui ne fonctionne certainement pas, car elle sera liée à un autre sujet.
L'énergie de différents champs peut-elle se détruire mutuellement?
Il y a une idée si intelligente sur la façon de se débarrasser de cette énergie. Il s'avère que:
• L'énergie des fluctuations des champs bosoniques (champs pour un photon, gluon, W, Z et Higgs, et même graviton) est positive,
• L'énergie des fluctuations des champs de fermions (champs pour un électron, un muon, un tau, trois neutrinos et 6 quarks) est négative!
Donc, peut-être, bien que l'énergie de chaque champ soit énorme, lorsque vous additionnez l'énergie de tous les champs, l'énergie totale se révélera-t-elle nulle - ou du moins très petite?
Vous pouvez effectuer de tels calculs, et dans le modèle standard, vous verrez que cela ne fonctionne pas; il y a trop de fermions, et dans l'espace vide il doit y avoir une énorme quantité d'énergie négative.
L'une des choses intéressantes de
la théorie de la
supersymétrie est qu'elle vous oblige à ajouter exactement les particules dont vous avez besoin (super partenaires pour chacun des types de particules connus) afin que vous obteniez automatiquement cette annihilation mutuelle! Et, en fait, c'est le seul type de théorie connu de l'humanité dans lequel cela est possible.
Malheureusement, cela ne résout pas réellement le problème de la constante cosmologique. Si la supersymétrie ne se manifeste pas explicitement [et cela est impossible dans notre monde - les masses de toutes les particules connues doivent être identiques aux masses de leurs super partenaires hypothétiques, et nous les aurions alors trouvées il y a longtemps], alors cette destruction mutuelle ne fonctionne que partiellement. La destruction partielle, qui peut réfuter le comptage 2, vous laisse encore une énorme quantité d'énergie du comptage 1. Comme indiqué sur la Fig. 3, cette quantité d'énergie gigantesque est suffisante pour que l'Univers se comporte très différemment de ce que nous voyons, sauf si quelque chose ne va pas avec la théorie de la gravité d'Einstein.
En bref, personne ne connaît aujourd'hui un moyen délicat de détruire automatiquement mutuellement la densité d'énergie des fluctuations de divers champs dans le monde décrits par le modèle standard jusqu'aux distances du LHC. En fait, personne ne sait même comment faire cela dans une théorie quantique des champs légèrement non supersymétrique (et encore, combiner la supersymétrie avec la gravité ravive ce problème).
En d'autres termes: même si nous permettons l'existence d'une annihilation mutuelle spéciale entre les champs bosoniques de la nature et les champs fermions de la nature, il semble que cette annihilation mutuelle ne peut se produire que par hasard, et dans une très, très petite fraction des théories quantiques des champs ou des théories quantiques de tout type (y compris la théorie des cordes ) Ainsi, seule une très, très petite partie des univers que vous pouvez imaginer peut au moins approximativement ressembler à la nôtre avec vous (ou au moins cette partie que nous pouvons observer avec nos yeux et nos télescopes). En ce sens, le problème de la constante cosmologique est un problème de naturalité, comme le terme est compris par les experts en physique des particules et leurs collègues: puisque l'Univers dans lequel nous vivons contient si peu d'énergie sombre par rapport à ce que nous attendons, notre Univers est très inhabituel et atypique.