Parmi les méthodes numériques utilisées dans le processus de conception des composants optiques modernes, deux grands groupes sont généralement distingués: universel pleine onde et approximatif. Le choix d'une approche spécifique dépend du rapport de l'objet simulé avec la longueur d'onde et de la nature de la propagation des ondes électromagnétiques.

Des méthodes à onde pleine basées sur la solution directe d'équations d'onde pour les composants du champ électromagnétique dans des conditions aux limites données sont généralement utilisées pour développer des micro et nanodispositifs optiques. Alors que pour la conception de systèmes macroscopiques tels que les lentilles de focalisation, les interféromètres et les monochromateurs, des méthodes approximatives sont utilisées. Celles-ci, en particulier, incluent le tracé géométrique des rayons.

Dans cet article, en plus d'une brève analyse de deux méthodes traditionnelles, nous parlerons d'une nouvelle approche appelée la méthode de l'enveloppe du faisceau et discuterons de ses avantages pour l'optique numérique.

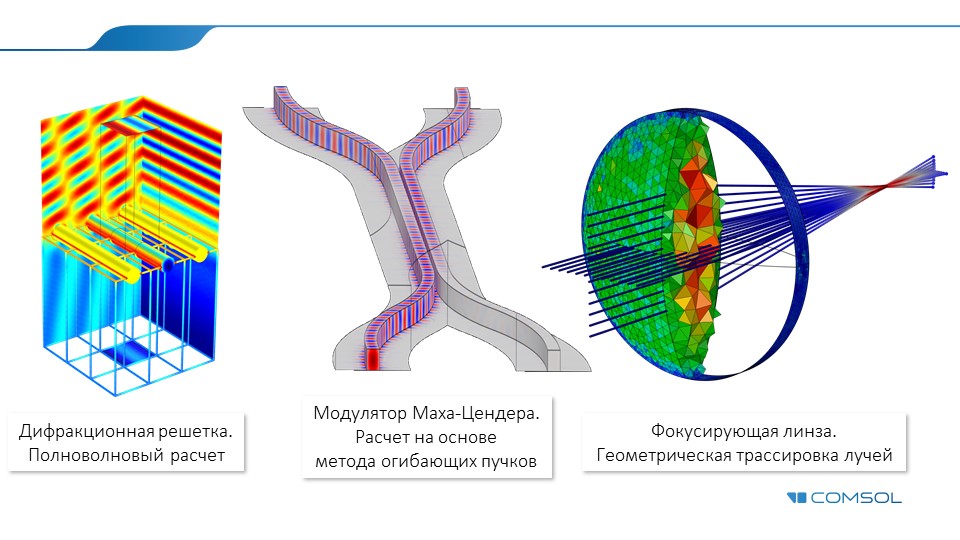
Méthodes pleine onde

Le premier groupe comprend la méthode spectrale, la méthode des moments, la méthode des différences finies et la méthode des éléments finis. Ils sont utilisés avec succès depuis de nombreuses années et sont activement utilisés aujourd'hui dans l'analyse de composants optiques importants tels que les structures de fibres optiques, les coupleurs directionnels, les résonateurs en anneau, etc. Grâce à ces méthodes, les ingénieurs et les chercheurs peuvent effectuer une analyse précise de la propagation des ondes dans les structures optiques en utilisant un ensemble minimal d'hypothèses physiques. Ces derniers sont associés à la discrétisation lors de la conversion d'un support optique continu par morceaux en un modèle numérique (discret). Ainsi, les phénomènes de diffraction, d'interférence et de modes de résonance de faible ordre peuvent être suivis avec une précision presque arbitraire, simplement en augmentant le niveau d'échantillonnage (Fig.1), tandis que ces méthodes elles-mêmes sont généralement appelées onde pleine (onde pleine).

Fig.1. L'incidence d'une onde électromagnétique plane sur une nanosphère d'or: une image d'un champ électrique diffusé et une grille d'éléments finis calculée.

En général, pour les méthodes de différences finies, l'augmentation du niveau de discrétisation se réduit à l'ajout de points supplémentaires au domaine de calcul et à l'obtention d'une représentation plus fluide du champ électromagnétique. Un principe similaire s'applique aux autres méthodes. Cependant, un plus grand nombre de points d'échantillonnage entraîne une augmentation des ressources de calcul nécessaires au calcul. Pour les modèles 3D, le nombre de ces points est proportionnel à la longueur d'onde dans le cube. Selon le critère de Nyquist, la longueur d'onde devrait avoir au moins deux points d'échantillonnage le long de chaque axe de coordonnées, et en conditions réelles - encore plus (généralement au moins 5 éléments de second ordre dans chaque direction spatiale). Dans la pratique, les coûts de calcul augmentent encore plus rapidement, par conséquent, pour calculer des objets qui correspondent à un grand nombre de longueurs d'onde (plus de 50), les méthodes pleine onde sont rarement utilisées en l'absence d'autres alternatives.

Un exemple simple: la largeur d'une fibre optique ne peut être que de quelques longueurs d'onde, et sa longueur est de plusieurs milliards de longueurs d'onde. Pour analyser les modes se propageant dans la section transversale de la fibre, les méthodes pleine onde sont excellentes car la taille relative de la fibre dans cette direction est petite (Fig. 2). Au contraire, pour analyser la propagation des ondes le long de la fibre et d'éventuels défauts de fibre, il faut recourir à des méthodes approximatives afin de ne pas épuiser la RAM de l'ordinateur.

Fig. 2. Calcul basé sur la méthode des éléments finis de la structure des fibres optiques: réseau d'éléments finis (à gauche) et l'un des modes de fibres transverses à une longueur d'onde de 1,2 μm (à droite).

Méthodes approximatives

Les méthodes approximatives impliquent l'utilisation de quelques simplifications ou approximations initiales. Cette classe de méthodes comprend des méthodes telles que le lancer de rayons (ou l'optique géométrique ), l'optique gaussienne et la méthode de propagation du faisceau (BPM) . Contrairement à l'approche pleine onde, dans certaines conditions, des méthodes approximatives peuvent être appliquées pour résoudre des problèmes sur des objets beaucoup plus grands.

Par exemple, des dizaines de milliers de longueurs d'onde de lumière visible s'insèrent dans une lentille d'un diamètre de 1 cm dans n'importe quelle direction. Dans ce cas, la méthode de traçage des faisceaux optiques est mieux illustrée. La contrepartie de l'approximation est le refus de prendre en compte certains phénomènes physiques: en optique géométrique, la diffraction est généralement négligée - les rayons se propagent en lignes droites (Fig.3).

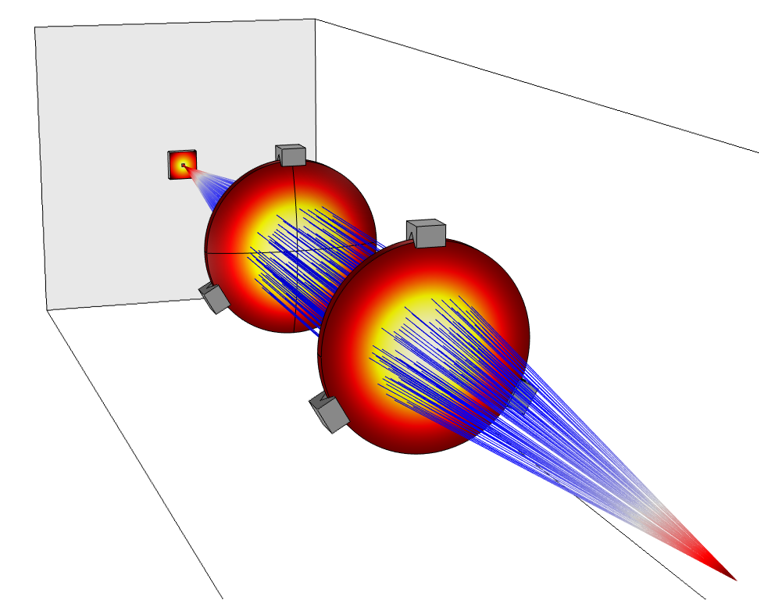
Fig. 3. Une analyse numérique de la propagation des ondes électromagnétiques dans un système de focalisation de faisceau laser est généralement basée sur le tracé de rayons, plutôt que de résoudre directement les équations de Maxwell par la méthode des ondes complètes.

Méthode d'enveloppe de faisceau

Les guides d'ondes dans les systèmes optiques ont généralement une direction préférée de propagation des ondes. Dans le langage de la physique mathématique, cela signifie qu'il existe un certain vecteur d'onde qui varie légèrement ou même reste constant dans le sens de la propagation. Une nouvelle méthode de calcul est basée sur cela - la méthode d'enveloppe de faisceau .

Dans le cas le plus général, le champ électrique d'une onde se propageant contient trois composantes: $$$E = (E_x, E_y, E_z)$. Supposons que l'axe z est la direction de propagation préférée et que le champ à l'intérieur de la structure du guide d'ondes oscille considérablement le long de l'axe z et contient des changements beaucoup plus lents dans les directions x et y . Ensuite, le champ d'une onde électromagnétique continue à fréquence constante peut être représenté comme $$$E = E_1 (x, y, z) cos (wt-k_zz)$où $$$w = 2 \ pi f$- fréquence angulaire, $$$k_z$Est la constante de propagation le long de l'axe z , et $$$E_1$- amplitude changeant lentement.

Cette expression sous une forme complexe $$$E = E_1 \ exp (i (wt-k_zz))$peut être substitué dans l'ensemble complet des équations de Maxwell et, en utilisant une série de transformations algébriques classiques, atteindre la réduction de tous les facteurs changeant rapidement $$$\ exp (i (wt-k_zz))$, obtenant l'équation finale pour une enveloppe de champ variant relativement lentement $$$E_1$. C'est sur cette réduction réussie de la composante à variation rapide que repose la méthode de l'enveloppe du faisceau . Pour revenir à la véritable expression d'une onde électromagnétique, il suffit de multiplier l'expression résultante par ce facteur.

En raison du manque d'approximations (la seule hypothèse concerne la direction de propagation des ondes initialement connue), cette approche peut être classée comme une méthode pleine onde (Fig.4), mais elle présente un avantage important. Le problème avec les méthodes pleine onde est qu'elles nécessitent un nombre suffisant de points de conception ou de nœuds dans l'échantillon, car Sinon, les résultats du calcul s'avéreront être simplement des «ordures» numériques. Pour résoudre l'équation d'une enveloppe de champ variant relativement lentement, un nombre beaucoup plus petit de points nodaux (tout en maintenant la validité du critère de Nyquist) est suffisant, au moins dans les cas où le problème a une direction de propagation clairement distinguée, comme, par exemple, dans les guides d'ondes optiques (Fig.4 ) Ainsi, le nombre requis de points d'échantillonnage ou de nœuds peut être réduit d'un ordre de grandeur (dans certains cas encore plus). Il est important de noter que toute méthode universelle peut être utilisée pour calculer l'enveloppe du faisceau, en particulier le FEM, puis pour obtenir une solution complète, il suffit de simplement multiplier l'enveloppe par une composante connue (donnée initialement) en évolution rapide.

Cette approche diffère considérablement d'une méthode de nom similaire - la méthode de propagation du faisceau, qui utilise des simplifications et des approximations supplémentaires, en négligeant certaines dérivées de l'équation d'onde.

Fig. 4. Comparaison de la discrétisation de la méthode traditionnelle pleine onde et de la méthode enveloppe de faisceau.

Méthode de l'enveloppe du faisceau et direction de propagation des ondes

La capacité de calculer des structures longues et minces avec une direction de propagation des ondes plus ou moins constante est très utile, et l'application de la méthode de l'enveloppe du faisceau à de tels cas est assez simple. Cependant, de nombreuses structures de guides d'ondes sont incurvées dans une ou plusieurs directions. La méthode proposée fonctionnera également dans ce cas, mais il existe certaines limites associées à la complexité géométrique de la conception. Si le vecteur de propagation change lentement de direction, la méthode reste valide. Pour comprendre ce qui se passe dans ce cas, revenons à l'expression complète du champ électromagnétique $$$E = E_1 \ exp (i (wt-k_zz))$, où la direction de propagation est initialement donnée le long de l'axe z . Pour généraliser cette expression au cas d'une direction arbitraire, nous l'écrivons sous la forme $$$E = E_1 \ exp (i (wt-k * r))$où $$$k = (k_x, k_y, k_z)$- un vecteur qui détermine la direction préférée de propagation des ondes, et $$$r = (x, y, z)$Est le vecteur de coordonnées $$$k * r$- leur produit scalaire.

En pratique, cette dernière est généralement fixée égale à la fonction de phase spatialement répartie $$$\ phi (x, y, z) = k * r = k_xx + k_yy + k_zz$. Ensuite, du point de vue du procédé d'enveloppe de faisceau, la condition de la direction de propagation qui change lentement est remplacée par la condition de la phase qui change lentement. Par exemple, la partie annulaire d'un résonateur de rayon R peut être décrite par la fonction de phase $$$\ phi = Rk_p \ arctan (y / x)$où $$$k_p = 2 \ pi / \ lambda_p$- constante de propagation correspondant à la longueur d'onde $$$\ lambda_p$dans le sens de la propagation (Fig. 6).

Fig. 6. Analyse du résonateur en anneau à une longueur d'onde de 1 559 microns. La grille d'éléments finis est montrée à gauche, un champ physique variant rapidement au centre et une enveloppe de champ variant lentement calculée en utilisant la méthode d'enveloppe de faisceau à droite.

Ainsi, le procédé d'enveloppe de faisceau peut être appliqué à des structures optiques composées de formes simples, où chaque composant composant peut être décrit par une fonction $$$\ phi (x, y, z)$correspondant à la direction de distribution locale préférée. Par exemple, un résonateur en anneau contenant une section directe et une section d'anneau peut être étudié en utilisant une fonction de phase constante et une fonction de «circulaire». Dans un cas plus général, la fonction de phase peut être définie comme l'interpolation d'une certaine dépendance simple du vecteur de coordonnées. De plus, en utilisant le principe de superposition des champs, il est possible d'analyser deux (ondes directes et arrière) et plus de directions de propagation (y compris les problèmes de réflexion et de réfraction), en enregistrant plusieurs ensembles de fonctions de phase (Fig.7).

Fig. 7. Distribution d'une enveloppe de champ variant lentement dans une cavité laser symétrique . Une superposition d'ondes (avant et arrière) se propageant dans deux directions est utilisée dans le calcul.

Application de la méthode de l'enveloppe du faisceau en optique non linéaire

Les effets optiques non linéaires sont souvent assez faibles et se produisent à de grandes longueurs d'interaction, et dans de tels cas, la méthode d'enveloppe de faisceau est la plus appropriée. Un exemple d'effets non linéaires est l'autofocus. Ce phénomène peut être observé dans des bâtonnets laser ou des verres optiques situés au point focal (par exemple, Nd: YAG - grenat d'yttrium-aluminium dopé au néodyme). La connaissance des valeurs seuils d'autofocalisation au stade de la conception évitera d'endommager les matériaux utilisés dans la construction de divers éléments (Fig. 8).

Fig. 8. Une étude numérique de l'autofocalisation dans une tige BK-7 de 20 cm de long , c'est-à-dire environ 300 mille (!!!) longueurs d'onde. L'image de droite est le rapport d'aspect réel, à gauche est la visualisation à l'échelle de la norme et de la composante z de l'enveloppe de champ.

La méthode est également applicable à d'autres effets non linéaires: génération de deuxième harmonique, génération de fréquence totale et de différence, génération et amplification paramétriques, ainsi que auto-modulation de phase.

Conclusion

La méthode de l'enveloppe du faisceau peut augmenter considérablement la taille des modèles auxquels les méthodes pleine onde sont applicables. Il comble l'écart entre des ressources informatiques exigeantes, mais des schémas précis de différences finies et d'éléments finis et des techniques de traçage rapide des rayons. L'approche est applicable aux problèmes de conception réels, ce qui confirme la solution réussie des problèmes appliqués, à la fois dans le domaine de l'optique non linéaire et des déclarations interdisciplinaires, par exemple, en calculant des modulateurs Mach-Zehnder .

Les développeurs de la méthode et de sa mise en œuvre dans COMSOL s'attendent à ce que sa combinaison avec des méthodes traditionnelles à onde pleine et approximative ouvre de nouveaux horizons en optique et en électrodynamique computationnelle pour une étude complète des processus e / m à différentes échelles spatiales.

PS Informations complémentaires

Cet article est basé sur des matériaux d' Optik & Photonik .

Pour une connaissance plus détaillée des méthodes décrites, nous vous invitons à participer à notre nouveau webinaire "Calculs pleine onde de composants optiques étendus dans COMSOL Multiphysics ^® " , qui se tiendra le 29 novembre 2017.