 UPD: graphique de fonction ajouté.
UPD: graphique de fonction ajouté.Comme son créateur Karl Weierstrass, ce monstre est venu de nulle part. Après avoir passé quatre ans à étudier à l'université pour boire et clôturer, Weierstrass en est sorti les mains vides. En fin de compte, il a commencé à enseigner et la plupart des années 1850 était professeur d'école à Brownsburg. Il était dégoûté de la vie dans une petite ville prussienne, il y a trouvé son existence seul. Le seul débouché pour lui était les problèmes mathématiques sur lesquels il travaillait entre les classes. Mais il n'avait personne avec qui parler des mathématiques et il n'avait pas de bibliothèque technique pour la formation. Même les résultats de son travail ne pouvaient pas quitter les limites de Braunberg. Au lieu de publier dans des revues universitaires, comme le ferait un chercheur universitaire, Weierstrass les a ajoutés aux avenues scolaires, effrayant les étudiants potentiels avec des équations abstruses.
En fin de compte, Weierstrass a envoyé l'un de ses articles au prestigieux
Crele Magazine . Malgré le fait que les articles précédents aient été à peine remarqués, cela a provoqué une énorme vague d'intérêt. Weierstrass a découvert un moyen de travailler avec la terrible classe d'équations connue sous le nom de «fonctions abéliennes». Un bref résumé de ses méthodes a été donné dans l'article, mais cela a suffi pour convaincre les mathématiciens du talent unique de l'auteur. Pas même un an ne s'était écoulé avant que l'Université de Konigsberg ne donne à Weierstrass un doctorat honorifique, et peu de temps après, l'Université de Berlin lui proposa le poste de professeur. Malgré le fait que Weierstrass ait fait un analogue intellectuel du chemin «des chiffons aux richesses», beaucoup de ses anciennes habitudes sont restées. Il publie rarement des articles, préférant partager son travail avec les étudiants. Mais il n'était pas seulement respectueux du processus de publication: les "vaches sacrées" des mathématiques ne lui faisaient pas peur.
Weierstrass a rapidement commencé à étudier le travail d'Augustin Louis Cauchy, l'un des mathématiciens les plus remarquables du siècle. De nombreux travaux de Cauchy ont étudié l’analyse mathématique et les taux de changement (ou «dérivés»). Il a créé les bases du dictionnaire de l'analyse mathématique, identifiant les concepts les plus importants de ce sujet. Mais quand Weierstrass a vu ses définitions, il les a trouvées verbeuses et vagues. Ils avaient trop de «gestes de la main» et peu de détails.
Il a décidé de réviser le vocabulaire de Cauchy, en remplaçant la prose par des conditions logiques. L'objectif principal de ses premiers travaux était de redéfinir le dérivé. Pour calculer le gradient d'une courbe en un point, et donc le taux de son changement, Isaac Newton a initialement considéré une ligne passant par ce point et le point voisin de la courbe. Puis il rapprochait de plus en plus ce point voisin, jusqu'à ce que la pente de la courbe devienne égale au gradient de la courbe. Mais ce concept était difficile à définir mathématiquement. Qu'est-ce qui indique la "proximité" de deux points l'un de l'autre?
Selon la définition verbeuse de Cauchy, le gradient "se rapproche infiniment d'une valeur fixe, de sorte qu'en conséquence il en diffère autant qu'il est nécessaire". Weierstrass ne pensait pas qu'une telle description soit suffisamment claire. Il voulait créer une définition plus pratique, alors il a décidé de transformer le concept en formule. Au lieu de manipuler des idées abstraites, les mathématiciens devraient pouvoir changer les équations. En travaillant là-dessus, il a jeté les bases de son monstre.
À cette époque, les mathématiciens étaient largement inspirés par la nature. Lorsque Newton a développé l'analyse mathématique, il s'est principalement inspiré du monde physique: les trajectoires des planètes, les oscillations du pendule, le mouvement des fruits qui tombent. Une telle réflexion a conduit à l'émergence d'une intuition géométrique concernant les structures mathématiques. Ils devraient avoir la même signification qu'un objet physique. En conséquence, de nombreux mathématiciens se sont concentrés sur l'étude des fonctions "continues". Ils peuvent être perçus comme des fonctions qui peuvent être dessinées sans déchirer le crayon du papier. Mettez la vitesse de la pomme qui tombe sur le graphique en fonction du temps et cela se révélera être une ligne continue, dans laquelle il n'y aura pas de coupures ou de sauts brusques. La fonction continue était considérée comme «naturelle».
Dans l'opinion alors généralement acceptée, un gradient pour tout nombre fini de points pouvait être trouvé dans n'importe quelle courbe continue. Cela semblait correspondre intuitivement: une ligne peut avoir plusieurs pièces inégales, mais il y a toujours plusieurs parties qui sont «lisses». Le physicien et mathématicien français André-Marie Ampère a même publié une preuve de cette affirmation. Son argument était basé sur le fait «intuitivement évident» qu'une courbe continue a des parties sur lesquelles elle augmente, diminue ou reste plate. Cela signifiait qu'un gradient pouvait être calculé pour ces zones. Ampère n'a pas pensé à ce qui se passerait lorsque ces pièces deviendraient infiniment petites, mais il a déclaré que ce n'était pas nécessaire. Son approche était suffisamment générale pour éviter de considérer les éléments "
infiniment petits " (infinitésimaux). Pour la plupart des mathématiciens, cette logique était suffisante: au milieu du XIXe siècle, presque tous les manuels d’analyse mathématique citaient la preuve d’Ampère.
Mais dans les années 1860, des rumeurs sont apparues au sujet d'une étrange créature - une fonction mathématique qui contredisait le théorème d'Ampère. En Allemagne, le grand Bernhard Riemann a déclaré à ses élèves qu'il connaissait une fonction continue qui n'a pas de parties lisses et pour laquelle il est impossible de calculer la dérivée d'une fonction à aucun moment. Riemann n'a pas publié de preuves, tout comme Charles Cellerier de l'Université de Genève, qui a écrit qu'il avait trouvé quelque chose de «très important et, il me semble, nouveau», mais il a caché son travail dans un dossier qui n'est devenu public qu'après sa mort pendant plusieurs décennies. plus tard. Cependant, si ses déclarations étaient crues, cela menacerait les fondements mêmes de l'analyse mathématique naissante. Cette créature menaçait de détruire l'amitié heureuse entre la théorie mathématique et les observations physiques sur lesquelles elle était basée. La matanalyse a toujours été le langage des planètes et des étoiles, mais comment la nature peut-elle être une source d'inspiration fiable s'il existe des fonctions mathématiques qui contredisent son essence fondamentale?
Le monstre est finalement né en 1872 lorsque Karl Weierstrass a annoncé qu'il avait trouvé une fonction continue, mais pas lisse à tous points. Il l'a créé en ajoutant une série infiniment longue de fonctions cosinus:
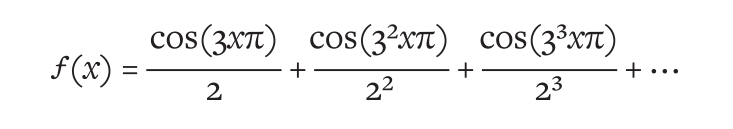
En fonction, elle était moche et dégoûtante. Il n'était même pas clair à quoi cela ressemblerait sur le graphique. Mais Weierstrass s'en fichait. Sa preuve n'était pas constituée de formes, mais d'équations, et c'est ce qui rendait sa déclaration si puissante. Il a non seulement créé un monstre, mais l'a également construit sur une logique de fer. Il a pris sa propre nouvelle définition rigoureuse du dérivé et a prouvé qu'il était impossible de le calculer pour cette nouvelle fonction.
Le résultat a plongé la communauté mathématique dans un état de choc. Le mathématicien français Emil Picard a déclaré que si Newton était au courant de telles fonctions, il n'aurait pas créé d'analyse mathématique. Au lieu d'héberger des idées sur la physique de la nature, il serait coincé dans des tentatives pour franchir des barrières mathématiques difficiles. Le monstre a commencé à assouplir les études précédentes. Les résultats, qui semblaient "prouvés", craquaient au niveau des coutures. Ampère a utilisé les longues définitions de Cauchy pour prouver son théorème de douceur. Maintenant, son témoignage commençait à s'effriter. De vagues notions du passé étaient impuissantes face au monstre. Pire encore, il devenait désormais difficile de comprendre en quoi consiste la preuve mathématique. Les arguments géométriques intuitifs des deux derniers siècles sont devenus inutiles. Lorsque les mathématiciens ont essayé de chasser le monstre, il est resté catégorique. Weierstrass a montré par une équation étrange que l'intuition physique n'était pas une base fiable pour construire des théories mathématiques.
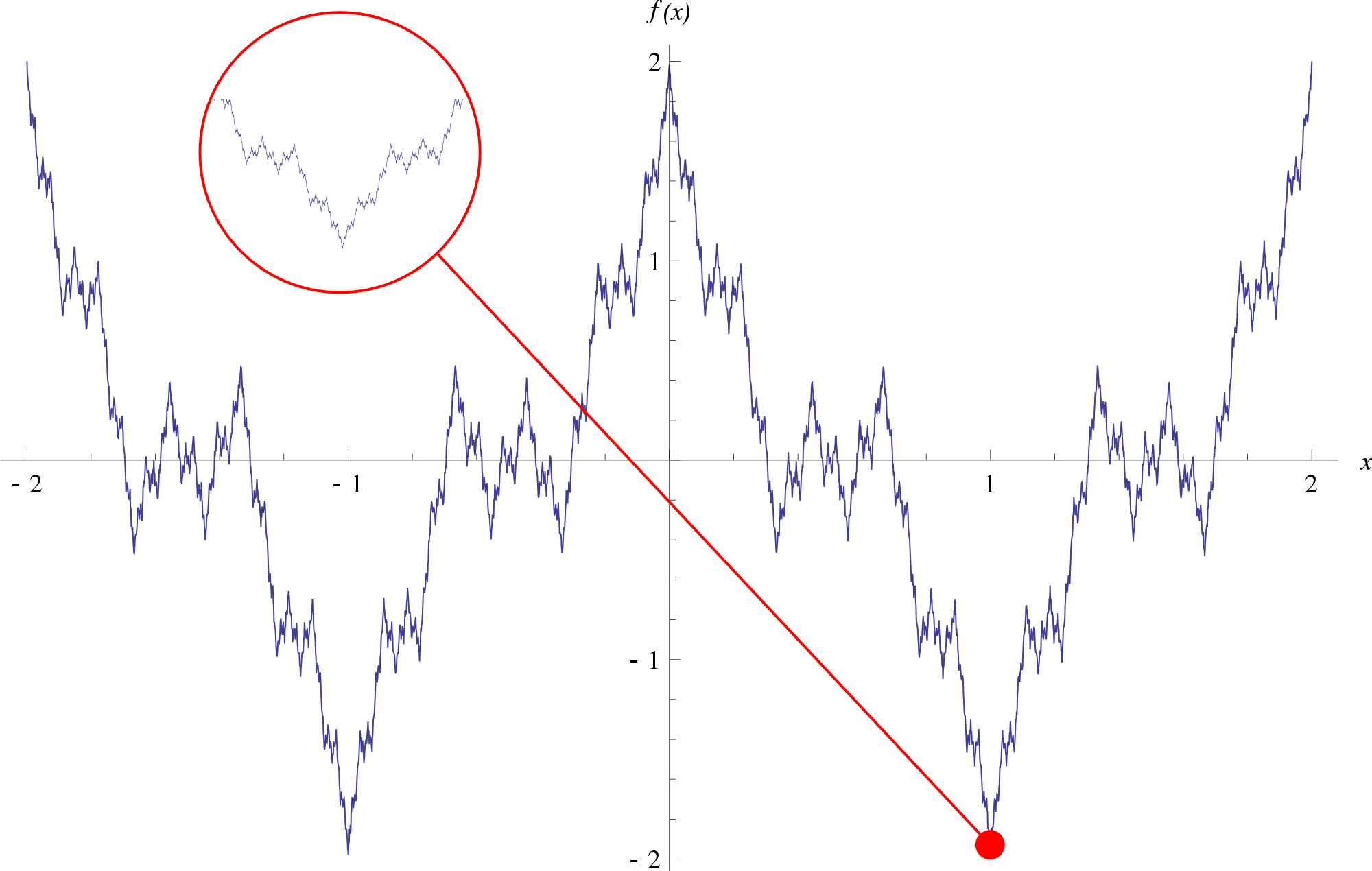
Des mathématiciens faisant autorité ont tenté d'écarter le résultat, arguant qu'il était laid et inutile. Ils craignaient que les rats de bibliothèque et les fauteurs de troubles ne créent le chaos dans leur domaine de connaissance préféré. Dans la Sorbonne, Charles Hermite écrivait: "Avec dégoût et horreur, je me détourne de la saleté regrettable de fonctions qui n'ont pas de dérives". Henri Poincaré, qualifiant pour la première fois de telles fonctions de monstres, a qualifié le travail de Weierstrass d '«insulte au bon sens». Il a soutenu que ces fonctions sont une distraction insolente de l'essence du sujet.
"Ils ont été inventés afin de montrer la fausseté des arguments de nos prédécesseurs", a-t-il déclaré. "Et en plus de cela, nous ne pouvons prendre aucun d'entre eux."
Beaucoup de "la vieille garde" voulaient laisser le monstre Weierstrass dans la cour des mathématiques. Il était également troublant que personne ne puisse imaginer la forme de l'animal qu'ils rencontraient - ce n'est qu'après l'invention des ordinateurs qu'il a été possible d'en créer un graphique. Sa forme incompréhensible empêchait la communauté mathématique de comprendre comment une telle fonction pouvait même exister. De plus, le style de l'épreuve Weierstrass était inconnu de nombreux mathématiciens. Sa preuve contenait des dizaines d'étapes logiques et s'étendait sur plusieurs pages. Le raisonnement était à peine perceptible et nécessitait de sérieuses connaissances techniques, mais dans le monde réel il n'y avait pas d'analogues qui aideraient à comprendre. L'instinct a exhorté à éviter cette preuve.

Mais les monstres ont la coutume de faire leur propre chemin. En fait, bon nombre des concepts qui semblent évidents aujourd'hui, voire nécessaires, étaient autrefois des monstres. Pendant des siècles, les mathématiciens ont rejeté les nombres négatifs. Les anciens Grecs, qui travaillaient principalement avec la géométrie, n'en voyaient pas la nécessité. Il en va de même pour les universitaires médiévaux qui ont adopté les idées des Grecs. L'ombre de ce monstre scintille parfois même aujourd'hui, par exemple, dans les questions d'un enfant demandant pourquoi, en multipliant deux nombres négatifs, cela se révèle positif. Mais en général, nous avons apprivoisé cette bête: personne ne veut le chasser à nouveau.
La même chose s'est produite avec le monstre Weierstrass - il a commencé à recevoir un appel. En 1904, Albert Einstein a initié les physiciens à l'idée de «mouvement brownien»: il a dit que les particules dans un liquide suivent des chemins aléatoires parce que les molécules liquides les repoussent constamment. Les collisions sont si fréquentes (supérieures à 10
21 par seconde) que, quelle que soit la qualité du microscope ou l'observation minutieuse, les trajectoires ne seront jamais lisses. D'un point de vue pratique, il leur est impossible de trouver un dérivé. Si les chercheurs veulent travailler avec de telles tâches, ils devront faire face au monstre Weierstrass. C'est exactement ce qu'a fait Einstein. Sa théorie était que dans le mouvement brownien des fonctions infiniment brisées étaient utilisées. Ceci est devenu un précédent important: depuis lors, les physiciens ont utilisé des fonctions non lisses comme approximation du mouvement brownien.
Quand il est devenu évident que les soi-disant «fonctions Weierstrass» étaient en fait très utiles, les scientifiques ont commencé à développer des façons de travailler avec élégance avec des fonctions non lisses. Au lieu d'analyser le trajet d'une particule individuelle dans un liquide, ils ont commencé à considérer le comportement moyen de nombreuses particules. Jusqu'où peuvent-ils voyager? Quand peuvent-ils atteindre un point donné? En dehors du domaine d'étude du mouvement brownien, les mathématiciens ont également commencé à repenser les outils de base de la matanalyse. Le taux de changement a toujours été déterminé par rapport aux distances et la zone sous la courbe a été mesurée géométriquement. Mais lorsque les fonctions n'étaient pas fluides, de telles idées n'avaient pas de sens.
Kiyoshi Ito de l'Université de Tokyo a découvert un moyen de contourner un problème en l'abordant en termes de probabilités. C'était une tactique peu orthodoxe, sinon risquée: dans les années 40, presque personne ne considérait la théorie des probabilités comme un domaine sérieux. Cependant, Ito a insisté de son propre chef. Il a abordé les fonctions comme des processus aléatoires et traduit les définitions de Weierstrass dans un nouveau langage basé sur les probabilités. Il a déclaré que deux processus aléatoires sont «proches» l'un de l'autre si leurs résultats attendus sont les mêmes. Il a introduit une méthode de travail avec une fonction mathématique, en fonction de la quantité de non-douceur, comme dans le mouvement brownien, au lieu d'une variable plus traditionnelle, par exemple, la distance. À l'aide de ses nouvelles méthodes, il a dérivé un «lemme Ito» pour calculer la variation d'une telle fonction au fil du temps.
Dans les années 1970, son travail s'est développé dans un tout nouveau domaine des mathématiques appelé calcul stochastique (les mathématiciens aiment appeler tout ce qui touche à l'aléatoire «stochastique»). Comme dans l'analyse elle-même, un ensemble entièrement nouveau d'outils et de théorèmes y est apparu. Aujourd'hui, le calcul stochastique est utilisé pour étudier toutes sortes de phénomènes, des neurones travaillant dans le cerveau à la propagation des maladies dans une population. Il est également devenu le fondement des mathématiques financières, dans lesquelles il aide les banques à mesurer la valeur des options. Il peut prendre en compte le comportement inégal du taux de change, ce qui signifie qu'il montre à quel point la valeur de l'option change avec le temps. L'équation résultante, connue sous le nom de formule Black-Scholes, est maintenant utilisée sur toutes les salles de marché du monde. Cependant, Ito a toujours été gêné par les éloges des banquiers. Il était un mathématicien théorique et ne s'attendait pas à ce que son travail soit connu grâce à une application pratique.
Le monstre Weierstrass a bousculé les principes de la géométrie. À la fin du XIXe siècle, le mathématicien suédois Helge von Koch s'est intéressé à l'idée des fonctions non lisses, mais a voulu étudier leur forme. Il s'est mis à créer une forme (plutôt qu'une fonction) qui ne sera lisse nulle part, montrant ainsi que les mêmes monstres se cachent dans l'algèbre avec la géométrie. Bien qu'il ne puisse pas dessiner la fonction Weierstrass, il a réussi à capturer son proche parent. Travaillant sur cette tâche dans le processus de recherche constante d'emplois temporaires en tant que professeur stagiaire, von Koch découvrit son existence en 1904. Il a pris un triangle équilatéral, puis a ajouté trois petits triangles de chaque côté, et ainsi de suite à l'infini. La forme géométrique résultante était continue, mais n'avait aucune dérivée. En raison de son apparence exceptionnelle, la figure est rapidement devenue connue sous le nom de «flocon de neige Koch».
Koch a réussi à étendre la puissance du monstre Weierstrass au-delà du monde des équations et des fonctions. Mais à la suite de son travail, il y avait autre chose qui méritait l'attention. En y regardant de plus près, il s'est avéré que son flocon de neige avait une curieuse similitude: agrandir une partie du flocon de neige et il ressemblera à une silhouette plus grande. Plusieurs années plus tard, il est devenu évident que la fonction Weierstrass a la même propriété.
Au fil du temps, une telle auto-similitude a commencé à se manifester dans toutes sortes de phénomènes. Afin de vulgariser l'idée des objets «fractals» dans les années 1980, le travail fondamental de Benoit Mandelbrot était nécessaire. Ces objets ont des formes qui se répètent à une échelle de plus en plus petite. Littoraux, nuages, plantes, vaisseaux sanguins - les mathématiciens ont découvert que les fractales sont omniprésentes dans la nature. Comme le flocon de neige de Koch, aucun d'eux n'était lisse. Et comment seraient-ils lisses? Si la figure a des parties lisses, le motif disparaîtra avec un grossissement suffisant. Comme l'a découvert Koch, la façon la plus simple d'obtenir une figure non lisse est de créer un objet fractal. Peut-être que le travail de Weierstrass devrait inévitablement conduire les mathématiciens à l'étude de modèles auto-similaires, introduisant les chercheurs dans le monde des structures magnifiques et exquises.
Le monstre Weierstrass continue son travail à ce jour. Les équations de Navier-Stokes décrivent le mouvement des fluides et sous-tendent la dynamique des fluides et l'aérodynamique modernes qui contrôlent tout, de la conception des avions aux prévisions météorologiques. Cependant, bien qu'ils aient été créés pour la première fois dans les années 1840, les mathématiciens ne savent toujours pas s'ils peuvent toujours être résolus. En 2000, le Clay Institute of Mathematics a offert un bonus de 1 million de dollars à quiconque pourrait prouver que ces équations ont toujours des solutions fluides - ou trouver un exemple du contraire. Ce problème est considéré comme l'un des six problèmes en suspens les plus importants en mathématiques, car malgré l'utilisation répandue des équations de Navier-Stokes, les mathématiciens ne savent pas si ces équations donnent toujours des résultats physiquement fiables. Le prix de 1 million de dollars n'est toujours réclamé par personne. À bien des égards, c'est un salaire pour la tête, incitant les mathématiciens à chasser les monstres dangereux.
Dans divers domaines: de la dynamique des fluides au secteur financier, des créatures comme les fonctions de Weierstrass ont mis en doute notre vision de la relation entre les mathématiques et le monde naturel. Les mathématiciens qui vivaient à l'époque de Weierstrass pensaient que les mathématiques les plus utiles étaient inspirées par la nature et que le travail de Weierstrass ne correspondait pas à cette définition. Mais le calcul stochastique et les fractales de Mandelbrot leur ont donné tort. Il s'est avéré que dans le monde réel - dans un monde réel chaotique et complexe - les monstres se cachent partout. Comme l'a dit Mandelbrot, "la nature a fait une blague avec les mathématiciens". Même Weierstrass lui-même est devenu la proie de cette astuce.
Il a créé sa fonction pour objecter que les mathématiques ne devraient être basées que sur des observations physiques. Ses disciples croyaient que Newton était limité par une perception intuitive du monde réel, et maintenant, libres de ces limitations, ils pouvaient découvrir de nouvelles théories plus universelles et élégantes. Ils pensaient que les mathématiques n'auraient plus besoin de la nature. Mais le monstre de Weierstrass a prouvé que tout était tout à fait le contraire. Le lien entre les mathématiques et la nature est beaucoup plus profond que tout le monde pourrait l'imaginer.À propos de l'auteur: Adam Kucharski est chercheur à la London School of Hygiene and Tropical Medicine, spécialisé en épidémiologie mathématique.