Une planète toroïdale peut-elle exister?

Après la publication de mon article sur ce que serait la Terre, si elle était deux fois plus grande, les lecteurs avaient la question: «Et la Terre toroïdale»? La question n'est pas la plus originale, ce sujet a déjà été discuté en ligne et sa modélisation a été réalisée. Mais j'aime tout faire moi-même, alors j'ai essayé de faire ma propre analyse.

Une planète toroïdale peut-elle exister?

La stabilité d'une planète toroïdale n'est pas évidente. D'un point de vue pratique, les planètes peuvent être considérées comme des boules liquides sans tension superficielle - la force d'une pierre ne peut être comparée au poids d'une planète. Ils possèdent des surfaces gravitationnelles équipotentielles tenant compte du potentiel centrifuge. Si ce n'était pas le cas, alors il y aurait des endroits sur eux qui pourraient réduire leur énergie en s'écoulant vers un potentiel inférieur. Un autre fait évident est l'existence de la limite supérieure de la vitesse de rotation, après quoi la planète va s'effondrer: la force centrifuge à l'équateur dépasse la gravité et le matériau s'envole dans l'espace.

Les formes d'équilibre des planètes ellipsoïdales tournantes tenues par la force de leur propre gravité ont été analysées de manière approfondie . Tout a commencé avec Newton, puis de premières expéditions héroïques ont été effectuées pour établir la forme de la Terre, Maclaurin a poursuivi son travail, Jacobi a découvert qu'à des vitesses de rotation élevées, les ellipsoïdes aux axes inégaux sont plus stables que les ellipsoïdes de Macloren aplatis. Subramanyan Chandrasekar a mené des développements intéressants dans ce domaine. Mais depuis lors, des ordinateurs sont apparus et, par conséquent, des calculs analytiques et numériques de cas plus complexes ou relativistes ont été effectués.

De la même manière, les formes d'équilibre des tores en rotation ont été analysées - cela a été fait par Poincaré , Sophia Kovalevskaya et Frank Dyson ( Dyson 1893 , Dyson 1893b ). Au moins en théorie, il est possible de dérouler une planète ellipsoïdale à un état d'anneau, bien qu'il existe de nombreuses possibilités pour que des oscillations se produisent qui déstabilisent le système, après quoi un saut à l'état d'anneau se produit.

L'anneau peut être instable, en particulier, en raison de l'instabilité "nodale" - une quantité croissante de masse peut s'accumuler dans certains méridiens, ce qui entraînera un espace dans plusieurs masses distinctes. Dyson a analysé ce cas et a constaté qu'il importait que R (la distance du centre du tore au centre du tuyau) dépasse r (le rayon du tuyau) plus de trois fois - c'est-à-dire que les cerceaux minces s'avèrent instables. Il y a aussi une vitesse de rotation inférieure à laquelle l'anneau devient instable et les forces de marée le compriment en un ellipsoïde . La masse totale et le moment angulaire doivent donc être réglés correctement dès le début.

Apparemment, les lois de la physique n'interdisent pas l'apparition de planètes toroïdales. La probabilité de leur occurrence est extrêmement faible, et une telle planète est susceptible d'être instable sur les échelles de temps géologiques en raison de perturbations externes. Donc, si nous supposons qu'elle existe déjà, peut-être en raison des actions d'une civilisation avancée dont l'esthétique est plus forte que l'esprit - quelles seront ses propriétés?

Directions

Nous appellerons deux cercles parallèles au plan de rotation des équateurs (externe et interne). Dans le cas où il n'y aura pas de différence fondamentale entre eux pour le sujet en discussion, je les appellerai simplement l'équateur. Les pôles seront les cercles les plus éloignés du plan équatorial.

La direction vers le centre indiquera la direction vers l'axe de rotation, vers la jante - depuis l'axe de rotation. Au plan - vers le plan équatorial. Nord - vers la partie la plus proche du cercle du pôle Nord, sud - vers la partie la plus proche du cercle du pôle Sud.

Gravité toroïdale

Comment fonctionne la gravité sur une planète toroïdale?

Dans le cas d'un très grand R, la planète toroïdale devient essentiellement cylindrique. Dans ce cas, la gravité diminue comme 1 / r, où r est la distance de l'axe. L'effet sur n'importe quelle section sera proportionnel à la masse totale (proportionnelle à R) et à la gravité (proportionnelle à 1 / R), de sorte que la force totale restera constante avec l'augmentation de R. Elle équilibrera une certaine rotation. Gravité superficielle 2G rho / r, où rho est la masse par unité de longueur. Donc, tant que la gravité de la surface est suffisamment grande (avec un petit r), cette force surmontera l'accélération centrifuge et ne s'envolera pas. Mais pour un tore avec un petit rayon, tout est beaucoup plus compliqué.

J'ai décidé d'utiliser la méthode de Monte Carlo pour évaluer la forme d'équilibre. En partant de la masse totale de la planète et de la quantité de mouvement angulaire, j'ai distribué beaucoup d'anneaux massifs infiniment minces (j'ai pris le potentiel de cet exercice - c'est bien qu'en physique classique le potentiel électrique et gravitationnel soit le même). J'ai calculé leur potentiel total et ajouté centrifuge. Cela nous permet d'approximer les surfaces équipotentielles et de «remplir» le potentiel plus près du centre du tore avec un nombre croissant d'anneaux, jusqu'à ce que leur masse corresponde à la masse de la planète. J'ai recalculé la vitesse angulaire en fonction de la nouvelle distribution de masse. Puis il a répété le processus jusqu'à ce que la planète soit dispersée, ou compressée en boule, ou que de nombreuses itérations soient passées. Ce n'est pas la méthode la plus élégante (dans la littérature la décomposition en une série d'harmoniques toroïdales est utilisée), mais c'était suffisant pour moi.

Le résultat principal est qu'une planète toroïdale permet de manière réaliste une masse et un moment angulaire suffisamment importants. La section n'est ni ronde ni elliptique, mais ressemble à un œuf, avec une courbure interne légèrement plus nette que l'extérieur.

Pourquoi la planète ne s'aplatit-elle pas en disque? La rotation essaie d'aplatir la planète, mais elle doit travailler contre la gravité locale, qui essaie de la comprimer en une boule (ou un cylindre).

Bien que dans ma simulation, ces planètes se soient avérées stables, la plage de valeurs acceptables n'était pas grande: la plupart des combinaisons de masse et de moment angulaire étaient instables. Je n'ai pas analysé la question complexe de l'instabilité nodale.

Je considérerai ici un tore joufflu avec une masse égale à la masse de la Terre et un petit trou central ("Donut"), ainsi qu'un tore plus large en forme de cerceau avec une masse de 6 terres mais plus proche de la gravité terrestre ("Hoop").

Beignet

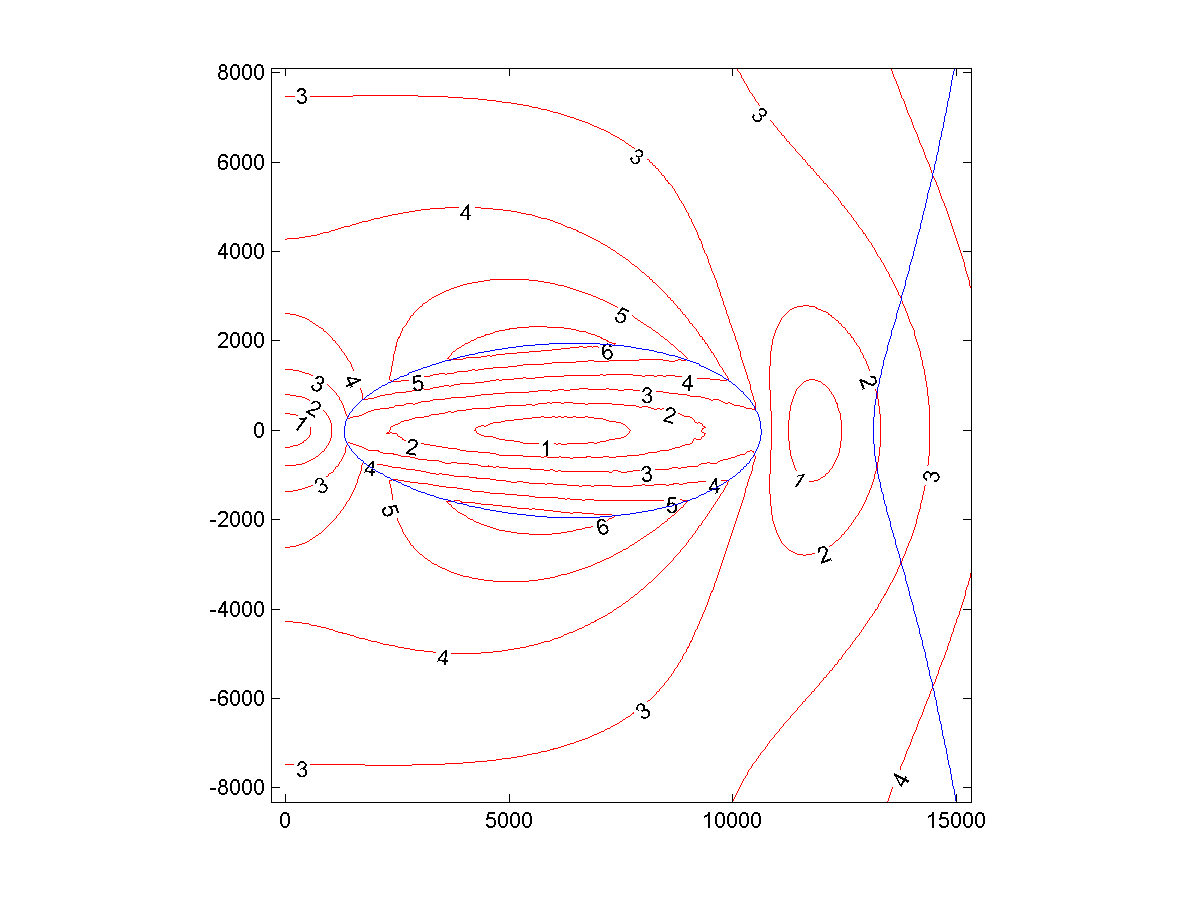Fig. 1: accélération gravitationnelle locale (m / s ² ) autour du Donut, ressentie par un objet tournant avec lui

L'équateur interne du Donut est à 1305 km du centre et l'extérieur - à 10663 km. Le diamètre de l'équateur est de 9328 km.

La planète s'étend sur une distance de 1953 du plan équatorial, et le diamètre du nord au sud est de 3906 km. Le rapport de diamètre est de 2,4.

La circonférence du nord au sud est de 21587 km (0,54 terrestre) et d'ouest en est - 66809 km (1,7 terrestre). La superficie totale est de 8,2 x 10 ⁸ km ² (1,6 terrain). Le volume total = 1,1 x 10 ¹² km ³ , ne diffère pas de la Terre de 1% au plus (après tout, le Donut a été choisi comme planète de la masse terrestre). Le rapport du volume à la surface - 1300, 61% de la Terre - par unité de volume de surface plus.

La journée dure 2,84 heures.

Cerceau

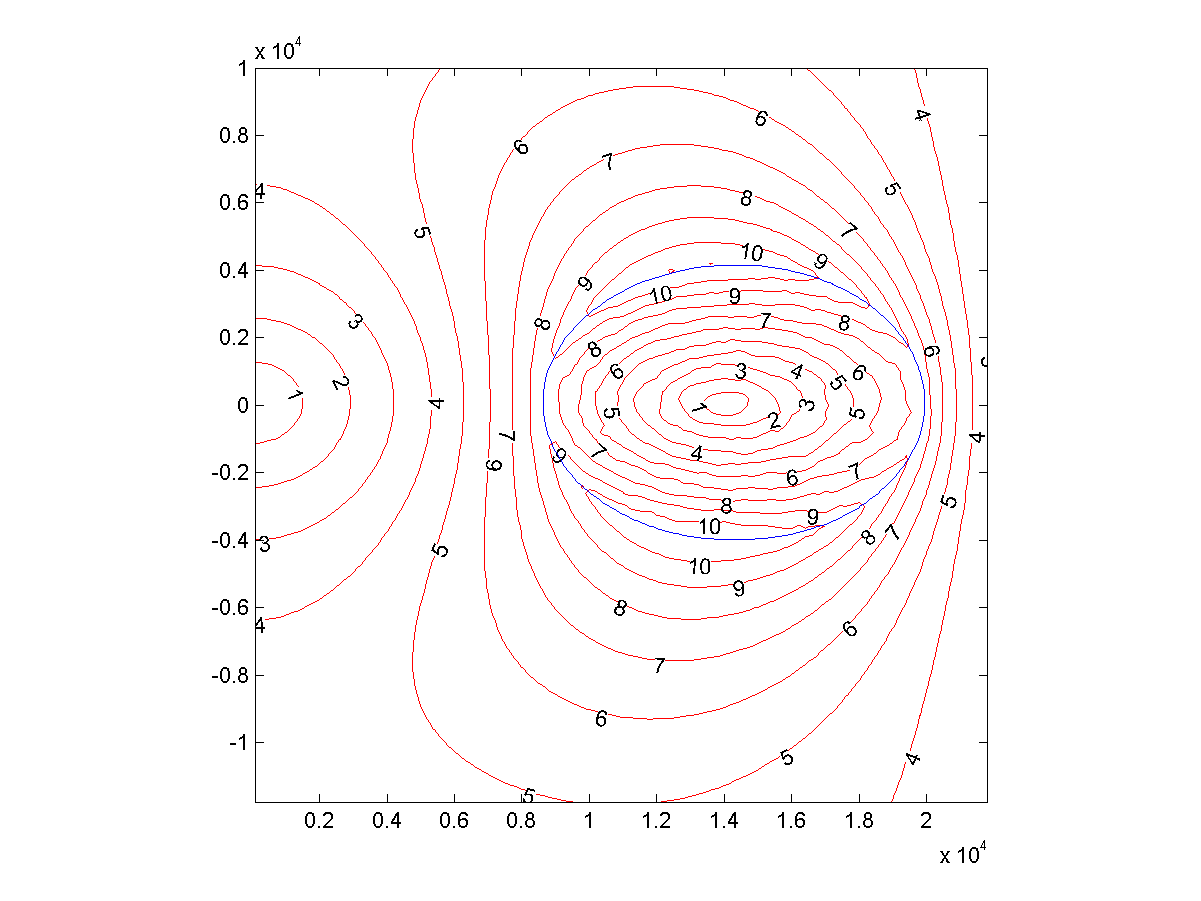
Fig. 2: accélération gravitationnelle locale (m / s ² ) autour du cercle, subie par un objet tournant avec lui

L'équateur interne de Hoop est à 8633 km du centre et l'extérieur - à 19937 km. Le diamètre de l'équateur est de 11 304 km.

La planète s'étend du plan équatorial sur 4070 km, diamètre du nord au sud - 8141 km. Le rapport hauteur / largeur de la section est d'environ 4: 3, comme avec les anciens moniteurs. Le rayon du cercle du centre de masse est de 14294 km.

La circonférence du nord au sud est de 30794 km (0,77 terrestre) et d'ouest en est - 125270 (3,1 terrestre). La superficie totale de 2,5 x 10 ⁹ km ² , 4,9 fois plus grande que la terre, et le volume total de 6,5 x 10 ¹² km ³ , 6 fois plus grande que la terre. Le rapport volume / surface = 150, 70% de la terre.

La journée dure 3,53 heures.

L'environnement

À quoi ressemble la vie sur une terre toroïdale?

La gravité

La gravité de la surface dépend de l'emplacement. C'est le plus faible le long des équateurs intérieur et extérieur, et le plus fort - près des pôles, légèrement vers le centre. C'est l'une des principales différences.

Beignet

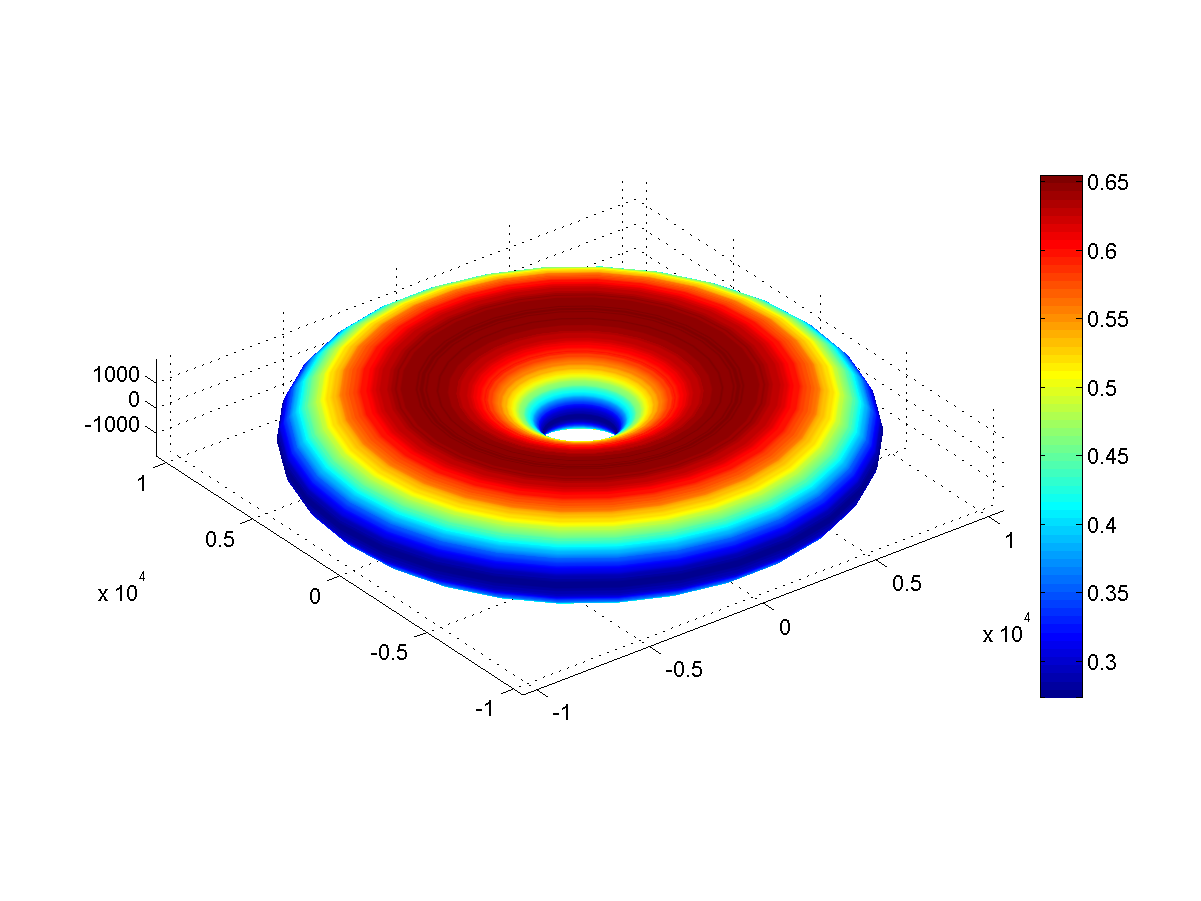Fig. 3: gravité de la surface du beignet (m / s ² )

Au Donut, la gravité le long des équateurs n'est que de 0,3 G et de 0,65 G le long des pôles. La vitesse de fuite n'est pas trop différente de la Terre et est égale à 11,4 km / s.

L'orbite géosynchrone autour du Donut est très proche de l'équateur externe, à moins de 2000 km. Un satellite volant le long de celui-ci restera au-dessus d'un endroit, mais, contrairement à la Terre, il ne pourra pas couvrir l'ensemble de l'hémisphère avec des engrenages, seulement une petite zone.

En revanche, la vitesse périphérique à l'équateur est de 6,5 km / s, et les lancements sont plus faciles à réaliser. Un missile lancé à l'est nécessite une vitesse de seulement 4,9 km / s pour s'échapper.

Au milieu du trou, il y a un point de Lagrange instable. Le satellite y sera attiré vers le plan équatorial, mais toute déviation de celui-ci augmentera.

Cerceau

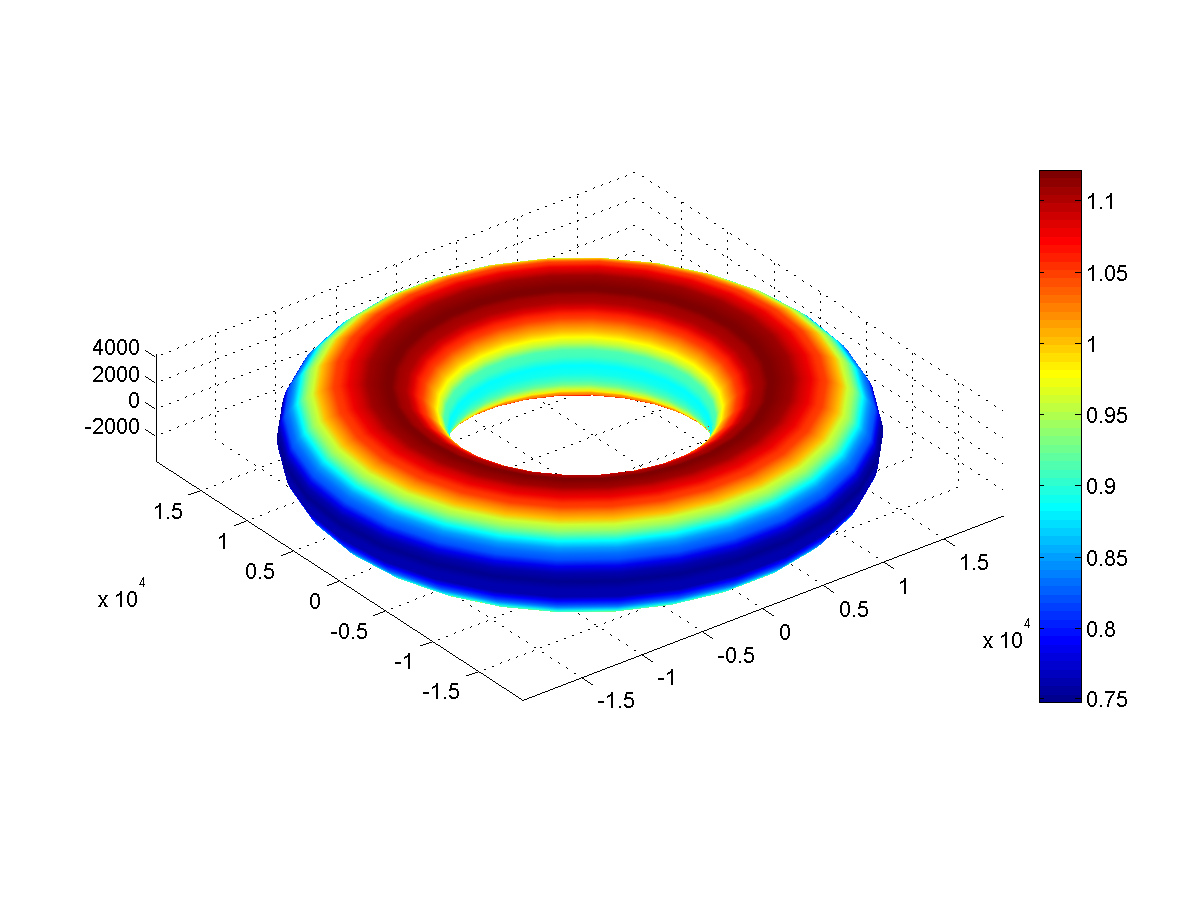Fig. 4: gravité de surface (m / s ² ) Cerceau

À Hoop, la gravité le long des pôles est de 1,1 G et le long de l'équateur externe - seulement 0,75 G. À l'équateur interne, elle est légèrement plus grande, environ 0,81 G.

La vitesse d'emballement est de 19 km / s (rappelez-vous que la planète pèse 6 fois plus que la Terre). À l'équateur externe, la vitesse d'emballement est de 9,9 km / s - une fusée lancée à l'est devra recevoir une vitesse de 10 km / s.

Encore une fois, je note qu'une faible gravité à l'équateur et élevée aux pôles ne signifie pas que les choses rouleront ou ramperont vers les pôles: comme déjà mentionné, la surface sera équipotentielle, de sorte que la gravité et la correction centrifuge seront toujours perpendiculaires à celle-ci.

Les masses d'air s'écoulant vers les pôles s'aplatiront. La différence de gravité créera une différence de pression horizontale qui, agissant avec la différence de température, créera des écoulements non triviaux.

La lumière

Les nuits et les jours sur de tels mondes seront très courts. L'environnement n'aura pas le temps de se refroidir ou de se réchauffer pendant les cycles quotidiens. Ce qui compte, c'est la différence de quantité de lumière reçue pendant des périodes plus longues, c'est-à-dire des saisons. Si ces mondes se déplacent sur une orbite similaire à la terre autour d'une étoile semblable au soleil, cela importera.

Si l'orbite est plus petite, les forces de marée rendront bientôt ces planètes instables. Étant donné que la luminosité d'une étoile augmente approximativement au quatrième degré de sa masse et que le rayon de la zone vivante augmente à mesure que la racine carrée de la luminosité, dans la zone résidentielle, l'échelle des forces de marée sera M / (√ (M ⁴ )) ³ = 1 / M ⁵ . Autrement dit, les effets de marée des étoiles brillantes seront beaucoup plus faibles - il est peut-être préférable que le beignet et le cerceau tournent autour d'une étoile bleue et blanche de classe F, et non pas autour d'une étoile de classe G, comme notre Soleil, juste au cas où.

La partie extérieure de la planète toroïdale n'est pas trop différente de la surface d'un ellipsoïde normal. Le jour vient où le soleil se lève sur l'horizon oriental et le coucher du soleil se produit sur l'ouest. Le soleil se déplace dans un grand cercle, se déplaçant lentement du nord au sud et en arrière au cours de l'année, ce qui assure la disponibilité des saisons. Cependant, tout est différent à l'intérieur de la planète. D'autres parties de la planète peuvent obscurcir le soleil - en première approximation, moins d'énergie peut être attendue.

Nous pouvons considérer trois cas différents: l'inclinaison de l'axe zéro, 23 degrés (comme la Terre) et 45 degrés.

Zéro inclinaison

Avec une pente nulle, la face intérieure du soleil ne verra pas: il sera toujours caché derrière l'horizon ou derrière l'arc du monde. Aux pôles, le soleil se déplace le long de l'horizon, et un peu plus près du centre il y aura toujours du crépuscule. Les différences de température seront importantes, la partie intérieure de la planète sera soumise à des températures subarctiques - ce qui n'est pas très différent du monde à rotation synchrone , et en principe, l'eau (et éventuellement le dioxyde de carbone) devrait toujours être condensée à ces endroits. En conséquence, il devrait y avoir des zones arides (peut-être pas trop chaudes) sur l'équateur externe, des régions presque polaires crépusculaires habitées et un intérieur glacial.

Inclinaison de 23 degrés

Fig. 5: saisons des beignets au printemps, en été, en automne et en hiver

Pour une pente de 23 degrés, coïncidant avec la terre, le printemps et l'automne coïncideront avec une pente nulle - lumière le long de l'équateur et sombre à l'intérieur, près du trou. En été comme en hiver, le soleil aura une chance de pénétrer derrière le rebord, de l'autre côté du trou. Il y aura également de grandes zones avec le soleil à minuit ou avec la nuit éternelle en été ou en hiver. Sur Terre, les régions polaires sont petites, mais ici ce seront de longs cercles continus.

Les levers de soleil du printemps et le crépuscule d'automne sur le côté intérieur devraient donner des couleurs profondes incroyables, car le soleil se lèvera à travers l'atmosphère de l'autre côté de la planète (précédemment levé ou couché, si je puis dire). Tout cela, combiné aux effets optiques atmosphériques locaux, produira des rouges et des dégradés très profonds. Immédiatement avant ou après le coucher du soleil ou l'aube, des parties de la couronne solaire seront visibles.

Ce spectacle aurait été plus impressionnant s'il n'avait été si court. Sur Terre, le soleil passe à environ 15 ° par heure. Dans le cas le plus rapide, le soleil passe un de son diamètre en 2,1 minutes. Sur le Donut, le soleil ira à 127 ° par heure, et sur Obruch - 102 °. Le lever et le coucher du soleil prendront respectivement 15 ou 19 secondes. L'angle incliné et les retards atmosphériques prolongeront légèrement la vue, mais pour un résident de la terre, ce sera trop court.

Si vous vous tenez sur le côté intérieur de la surface et regardez vers le haut, l'autre côté occupera 20 degrés du ciel sur Obruch et 30 degrés sur le Donut - une énorme arche à travers le ciel entier.

Pourquoi le beignet n'est pas beaucoup plus large? Il est très plat, il semble donc plus court dans le ciel. En passant, cela signifie que lorsque la lumière du soleil est réfractée à travers l'atmosphère de l'autre côté à l'aube ou au coucher du soleil, les couleurs rouges seront beaucoup plus profondes que sur Obruch.

À l'intérieur, la partie opposée éclairée du tore illuminera tout à la manière du clair de lune. Mais la surface sera plus grande, donc les nuits seront beaucoup plus lumineuses. Sur Obruch, la lumière sera 16 000 fois plus forte que la Terre (8 000 lux) lorsque toute la partie opposée sera illuminée (prenons l'albédo égal à la Terre), et la nuit sera comme un jour nuageux. Sur le Donut, l'éclairage atteindra une lumière du jour faible (12 000 lux). Mais c'est la situation du côté opposé complètement éclairé - pendant l'équinoxe, seule une fine bande sera visible.


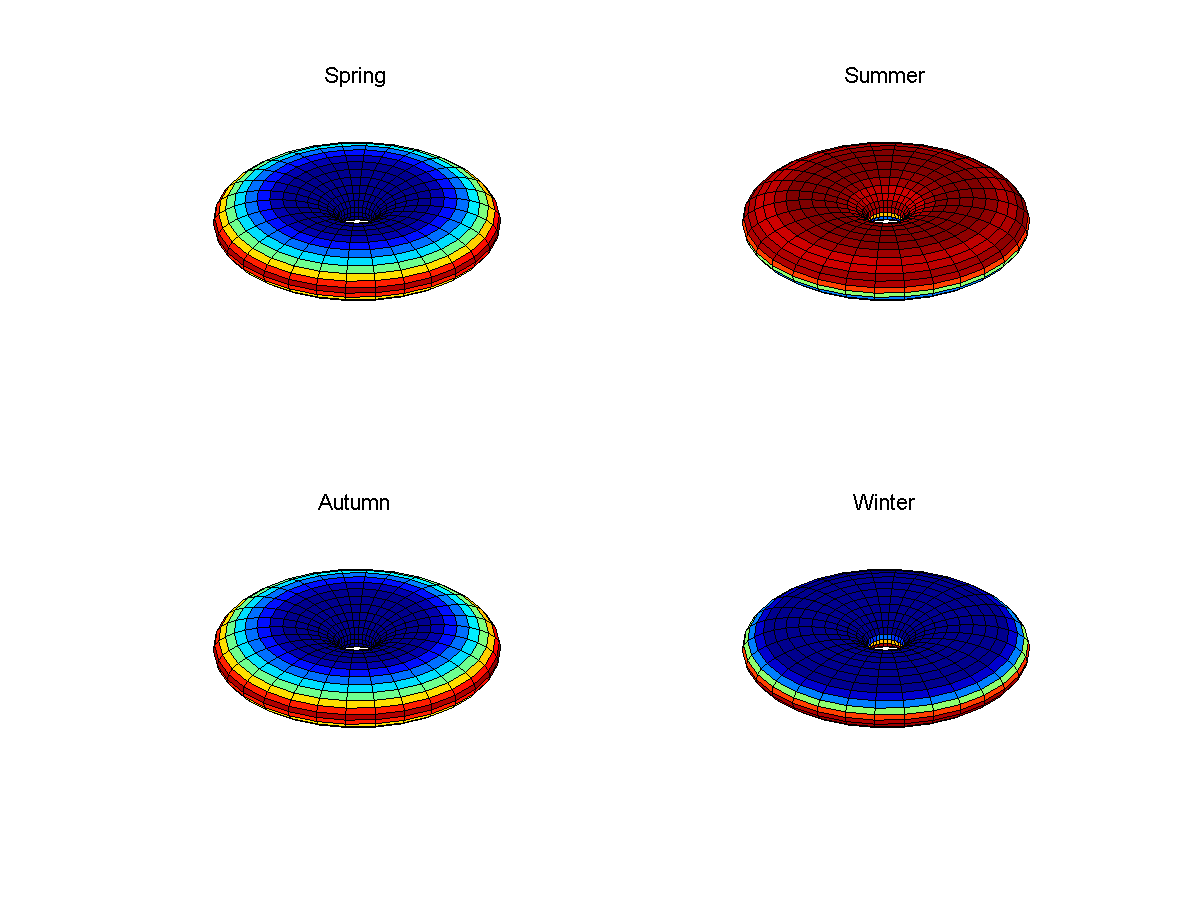Fig. 6: éclairage quotidien moyen sur le Donut au printemps, été, automne et hiver pour le boîtier avec une pente de 23 degrés

Dans le cas du Donut, une surface assez plate signifie que l'hémisphère nord ou sud (un an et demi) recevra beaucoup de soleil. L'échauffement total de la planète sera plus important durant ces saisons qu'au printemps et en automne, contrairement à la Terre, où il est constant, car la zone recevant la lumière reste constante. Des effets non triviaux seront également observés en raison des angles entre la surface et la lumière du soleil, et les zones tempérées recevront un peu moins d'énergie que les régions polaires et les tropiques.

Sous les tropiques extérieurs, il y aura approximativement le même afflux d'énergie solaire. Vers les pôles, la saisonnalité se fait plus fortement sentir: les tropiques en été reçoivent à tout moment plus d'énergie que l'équateur. Les hivers seront tout aussi sombres. Aux pôles et derrière eux, à l'intérieur, dans des endroits à gravité maximale, le soleil sera visible pendant six mois, puis il y aura une nuit polaire. Ici, le climat va changer radicalement - sur les tropiques extérieurs au moins, il y aura des nuits pendant 1,5 heure, et ici, elles dureront 6 mois. Enfin, plus près de l'équateur interne à côté du trou, le jour et la nuit seront égaux en hiver (et la lumière réfléchie par l'autre côté sera également ajoutée), de sorte que la température sera légèrement plus élevée.


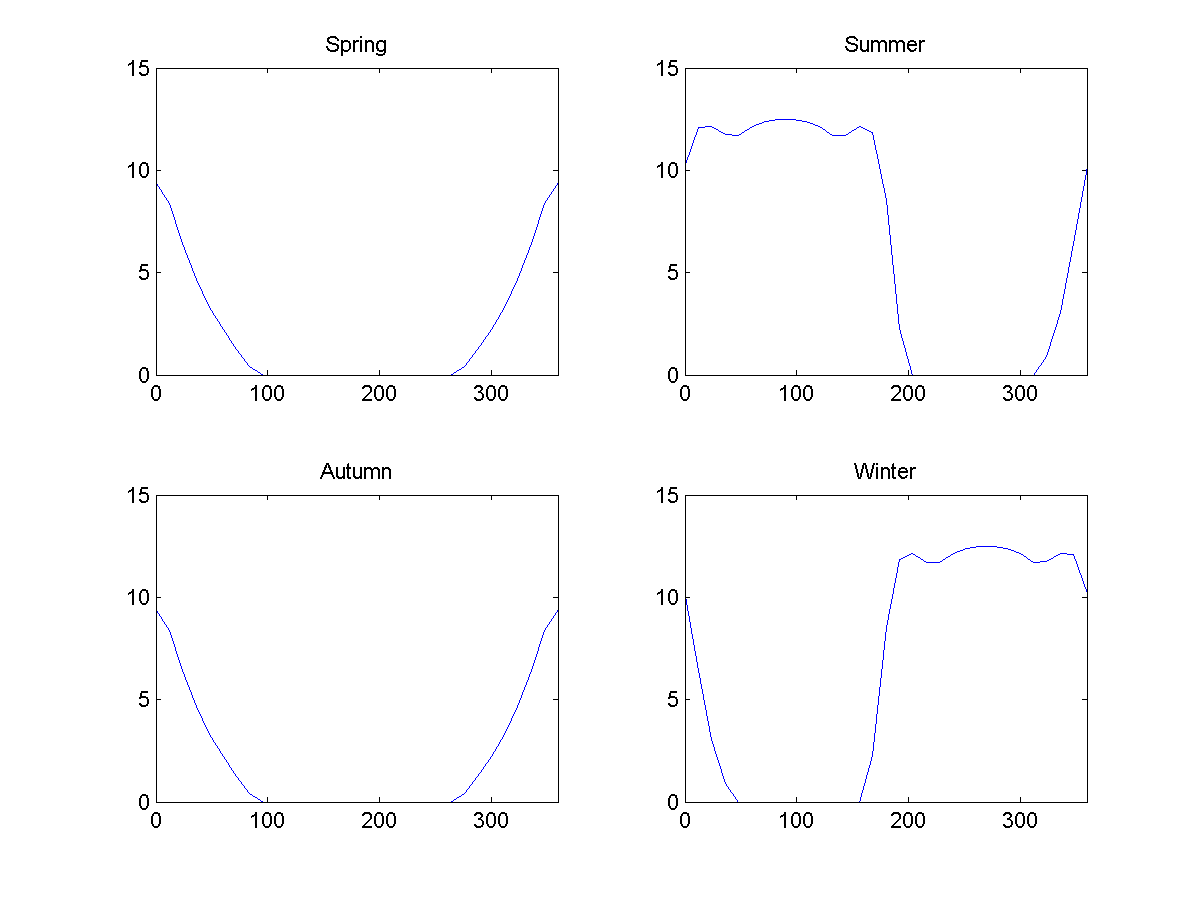Fig. 7: illumination moyenne pendant différentes saisons sur le Donut, en fonction de la latitude dans le cas de 23 degrés. 0 signifie l'équateur externe, 90 signifie le pôle nord, 180 signifie l'équateur interne, 270 signifie le pôle sud.

Une grande différence dans la quantité d'énergie reçue du côté ensoleillé de l'été du trou et du côté sombre de l'hiver du trou entraînera des conditions météorologiques violentes - mais en raison d'autres bizarreries de ces mondes, il sera plus difficile d'égaliser la différence d'énergie que sur Terre.

En moyenne, la partie extérieure équatoriale recevra 2,5 fois plus d'énergie que les parties polaires, et la partie intérieure recevra quatre fois moins d'énergie que les zones environnantes.


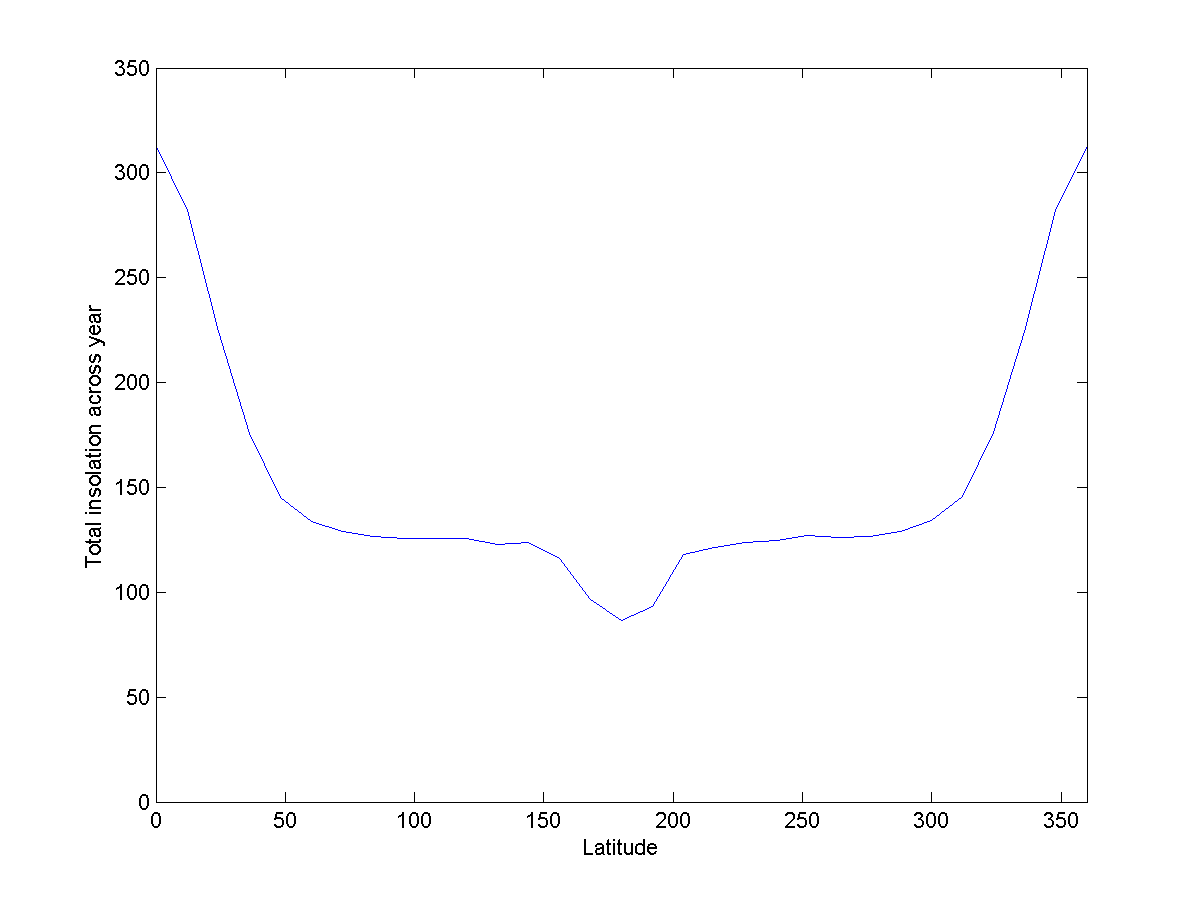Fig. 8: énergie sous différentes latitudes du Donut

Le cerceau projette moins d'ombre sur lui-même. Plus important encore, il n'est pas aussi plat que le Donut.


Fig. 9: illumination moyenne pendant la journée sur Obruch, 23 degrés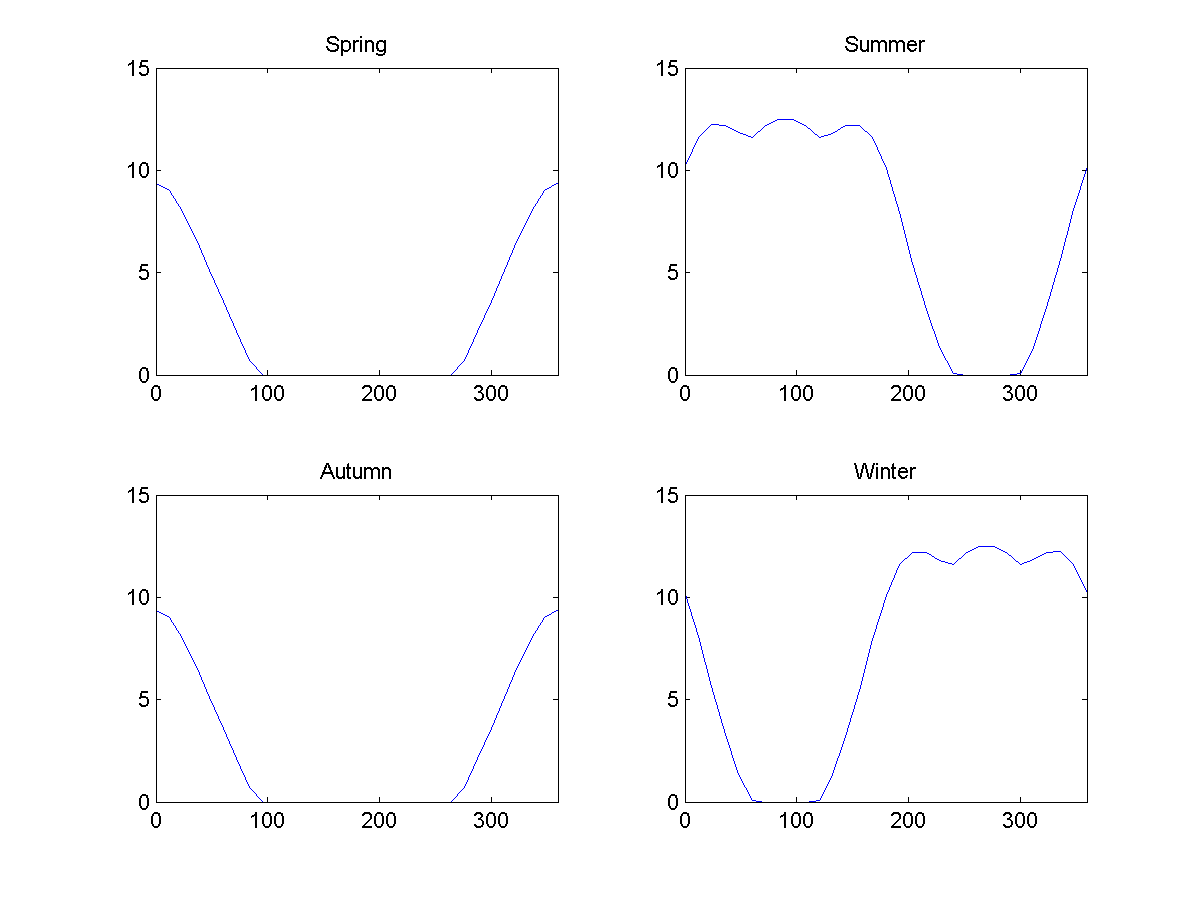


Fig. 10: illumination moyenne pendant différentes saisons sur Obruch, en fonction de la latitude dans le cas de 23 degrés. 0 signifie l'équateur externe, 90 signifie le pôle nord, 180 signifie l'équateur interne, 270 signifie le pôle sud.

À première vue, les saisons se présentent comme prévu. Au printemps et en automne, les parties intérieures seront cachées à l'ombre, en été et en hiver, une région polaire est éclairée plus fortement, et l'autre est plus faible, et les parties intérieures recevront leur éclairage. Cela conduira à la présence d'un cycle saisonnier dans la partie intérieure de la planète, allant deux fois plus vite qu'à l'extérieur (ce sera le cas sur le Donut): le temps sera chaud en juillet et janvier.


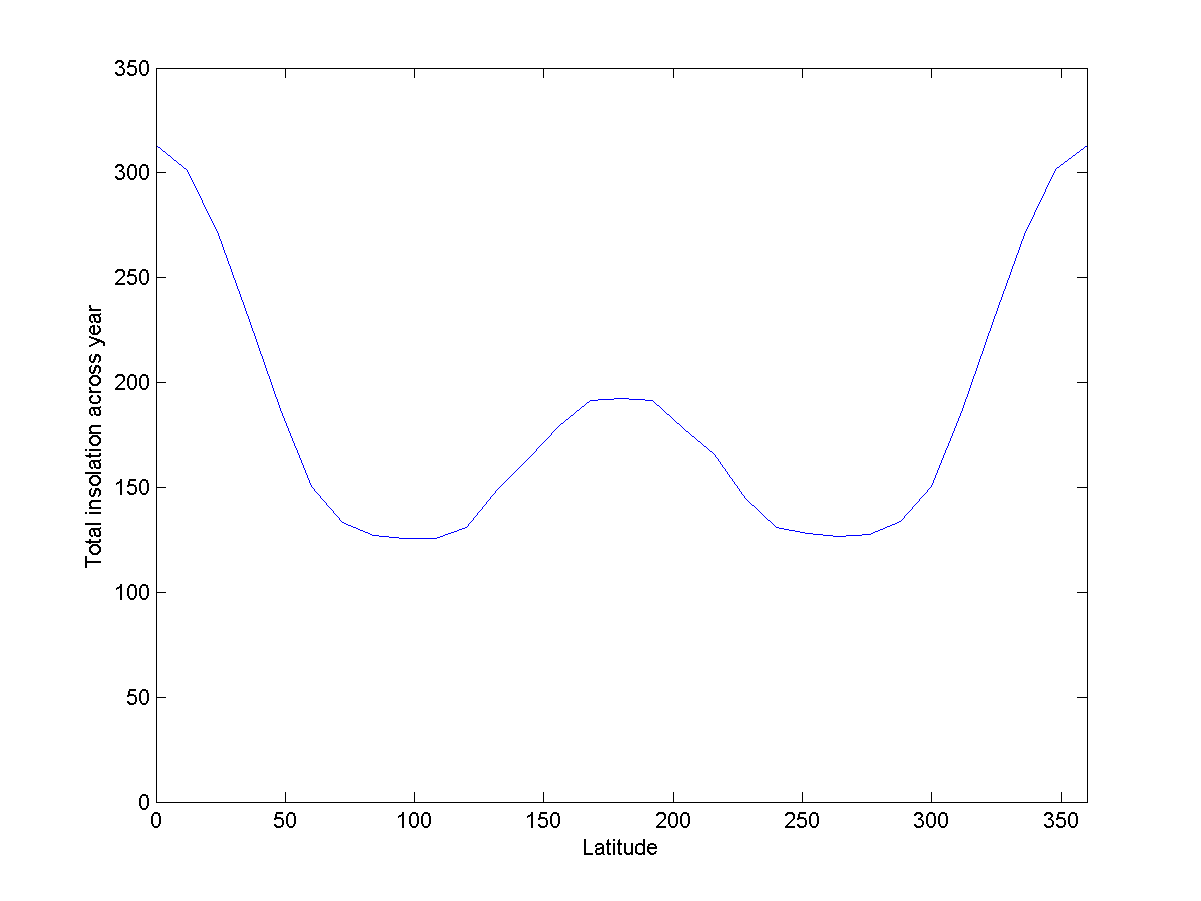Fig. 11: énergie reçue au cours de l'année sous différentes latitudes du Cerceau

Comparé à Donut, cela ne sera pas intuitif - l'équateur interne reçoit plus de lumière pendant l'année que les régions polaires. On peut s'attendre à ce que le climat ressemble à la Terre - les régions polaires sont plus froides, les régions équatoriales sont plus chaudes. 60%.

45

, – , !

, , 90 – , . , . , . – . , .


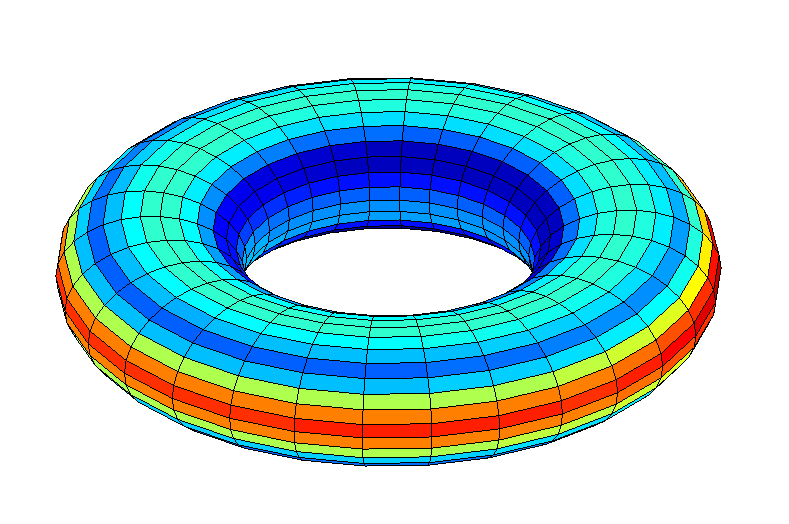Fig. 12: , 45

, 10% . .

, . .

, ( 1300 , 1500 , – 2124 ). , , . - . 6 , , 5 .

. , r R 2 π r , r/R. , , 43% . – 12% ! , , , , , . .

. , 1,5 ( 12 ), 3 (24 ). , .

. , , . - , .

, , , . , .

, , , . , «» , , : , , . : , , .

8 , . , , . , , , , . , – .

, (Intertropical Convergence Zone, ITCZ) , , , (), , , ( ). , , ITCZ , . , 30 ( , , ).

, , . : , , , .

, , . 1,5-3 , , .

, . – . ( ). , .

, , 6 , 5 , 20% - ( 20%). , , .

: , . ; , , . , . , , . , , .

: , . 150% . (133% , 90% ). .

, . , , . , , (, , ). , , – .

Ces mondes pourront-ils contenir la lune?

La lune en orbite dans le plan de l'équateur sur une orbite circulaire près du tore ne ressentira aucune différence par rapport à une planète ronde. Cependant, lors de l'acquisition de l'excentricité, les choses se compliquent. Un champ potentiel à l'approche d'une planète tombe plus lentement que 1 / r, comme sur les planètes normales: l'ellipse de Kepler ne convient plus comme solution. Avec l'inclinaison de l'orbite, le système devient encore plus complexe - maintenant la lune ressentira la planéité de la planète.

Dans un sens, les développeurs de satellites sont déjà confrontés à un problème similaire: la Terre est suffisamment aplatie aux pôles pour la rendre visible. Ce problème a été résolu dans les premiers stades du voyage spatial (Wikipedia, (Tremaine & Yavetz 2013) ou (Nielsen, Goodwin, & Mersman 1958).

En fait, une orbite elliptique est soumise à une précession - elle change progressivement de direction, et dans le cas de la Terre, cela dépend de l'inclinaison de l'orbite. L'excentricité peut aussi nager. Dans tous les cas, pour un tore, ces effets seront plus prononcés. Ils seront si solides que les méthodes de calcul standard ne fonctionneront plus, et nous devrons effectuer des simulations informatiques.

Je suis sûr que les lunes dans des orbites circulaires suffisamment éloignées se comporteront de manière assez stable. Très probablement, ils seront soumis à la précession, donc leur orbite ressemblera plus à une douille qu'à une ellipse, mais ils ne s'envoleront pas des bobines. Bien sûr, si l'orbite de la lune est plus proche, tout sera différent.

Dans la simulation (je n'ai pas utilisé de tore complet, mais un anneau de 30 masses), plusieurs possibilités m'ont été ouvertes. L'orbite elliptique équatoriale semble nette et stable, mais la précession la transforme en douille.



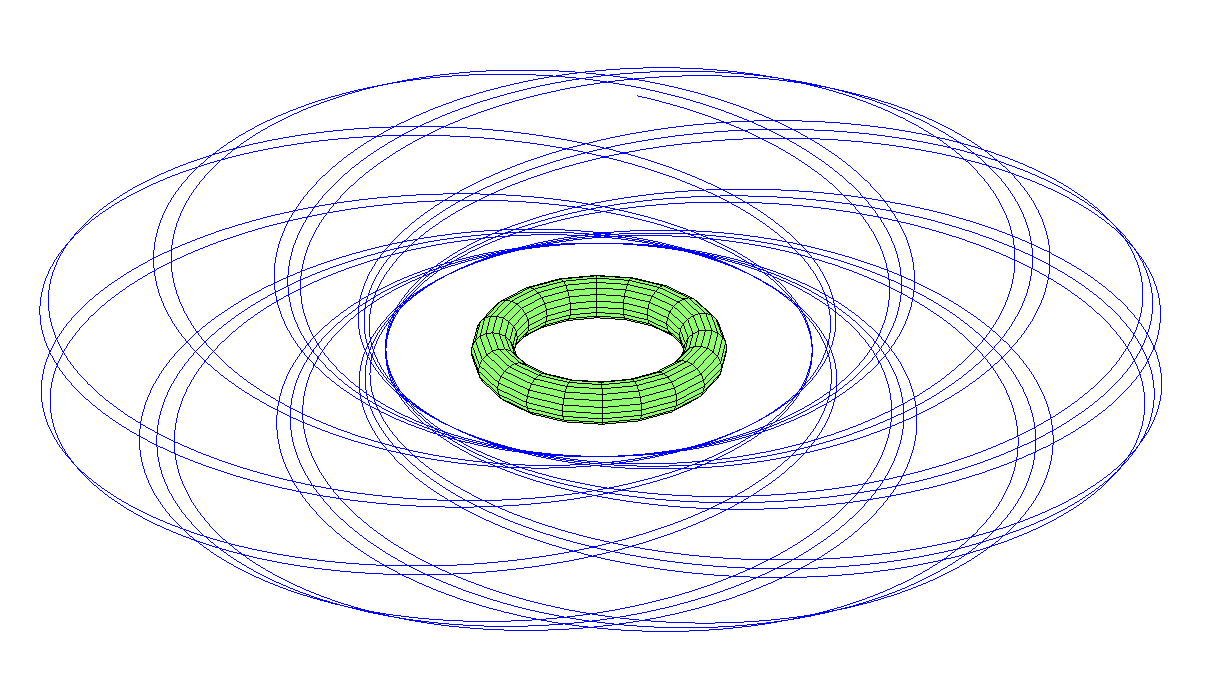
L'orbite circumpolaire précède encore plus, non seulement la sortie apparaît, mais aussi la précession de l'avion. La lune dans le ciel peut apparaître dans n'importe quelle constellation.



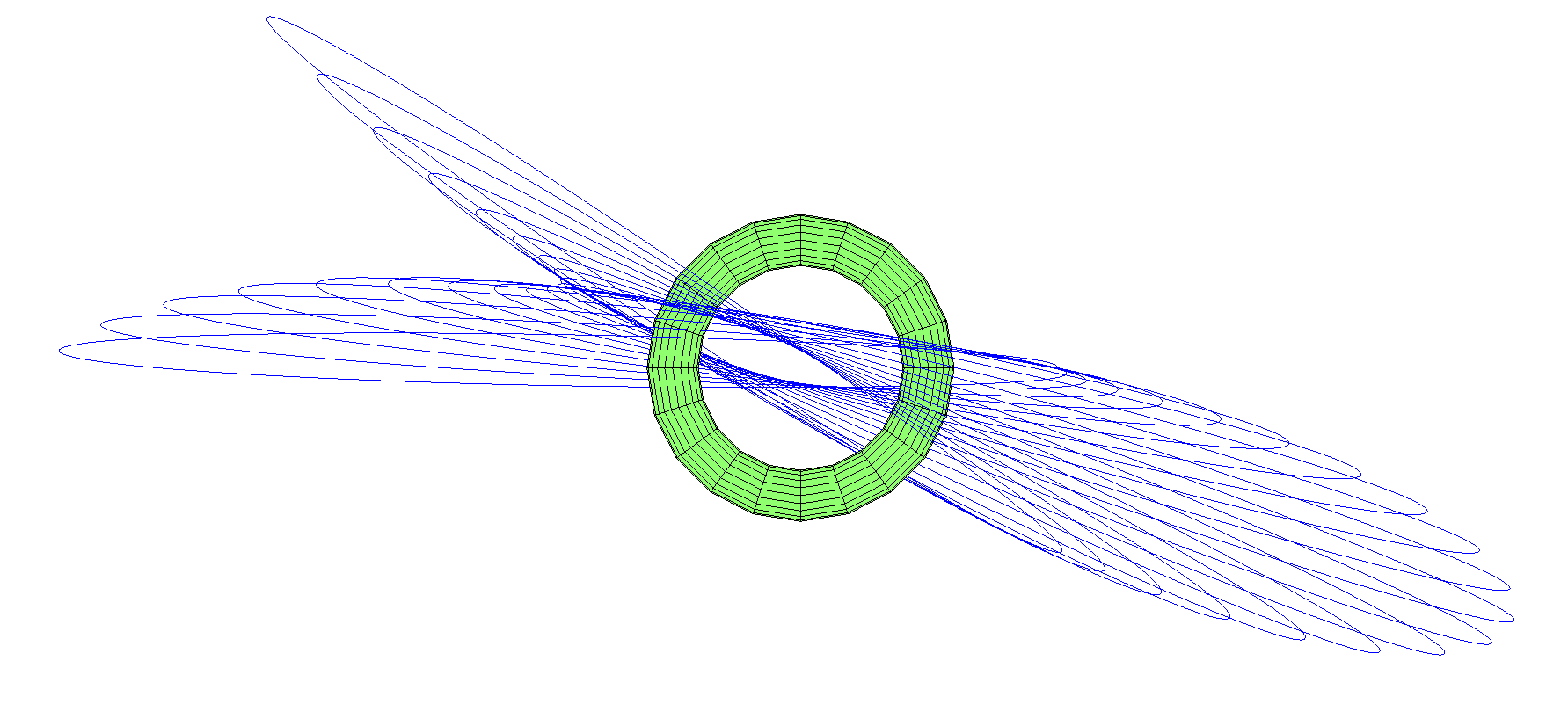
Et les orbites qui traversent le trou? Comme je l'ai noté précédemment, le centre géométrique est un point de Lagrange instable. Si vous placez la lune là-bas, tout coup la fera sortir de là. Mais il y a des orbites qui semblent stables à travers le centre (plus précisément, sous n'importe quel impact, elles se transformeront en une autre orbite de forme similaire). L'option la plus simple est la lune, qui va et vient à travers un trou, comme un pendule:



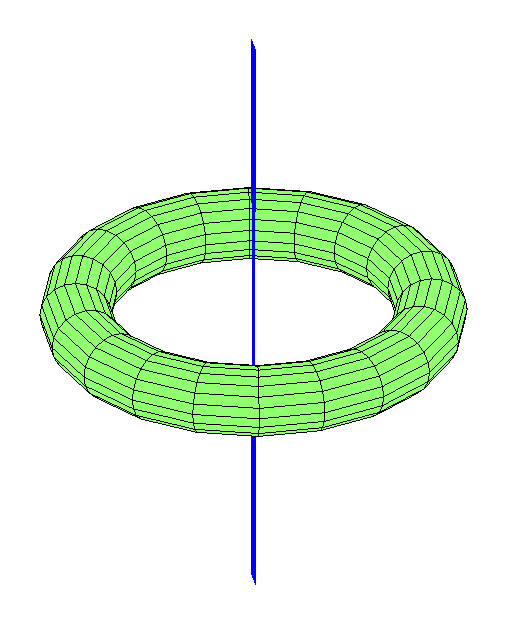
Vous pouvez imaginer la lune voler à une certaine longitude:



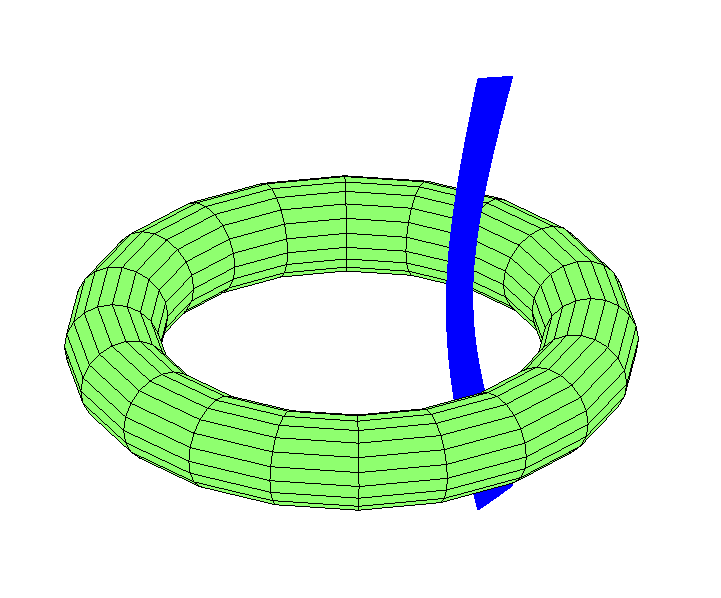
Avec l'acquisition de la vitesse en longitude, il se déplacera dans le trou:



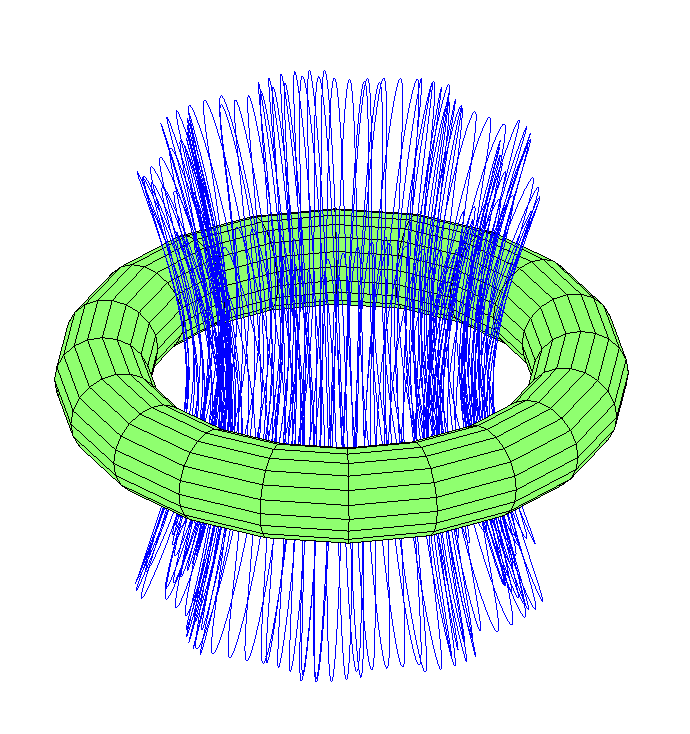
Qu'en est-il des trajectoires passant par un trou dans une direction? Il s'est avéré qu'il y a pas mal de huit orbites qui dessinent une grosse boule toroïdale.





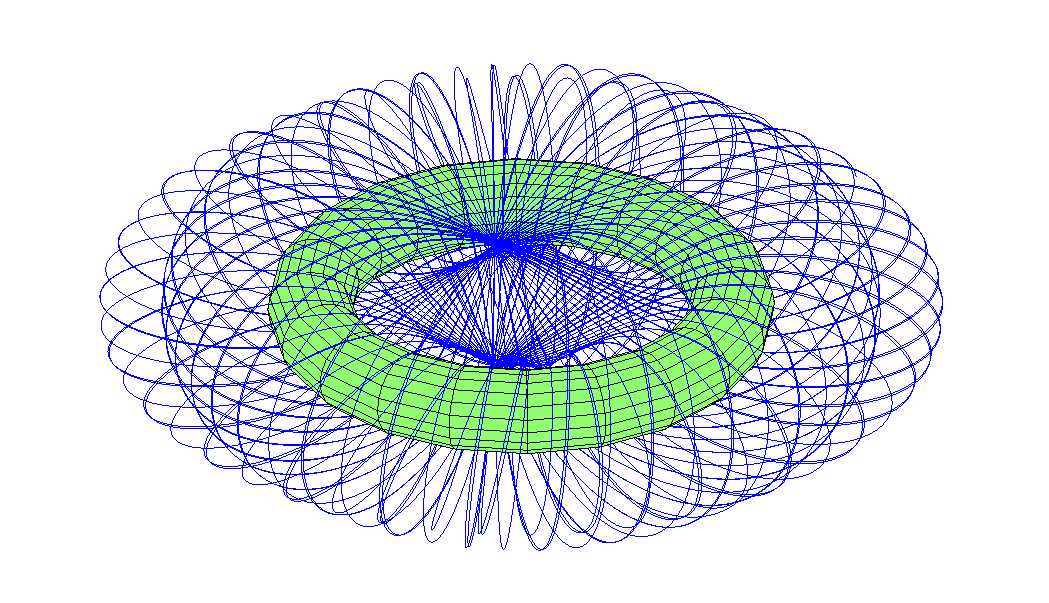
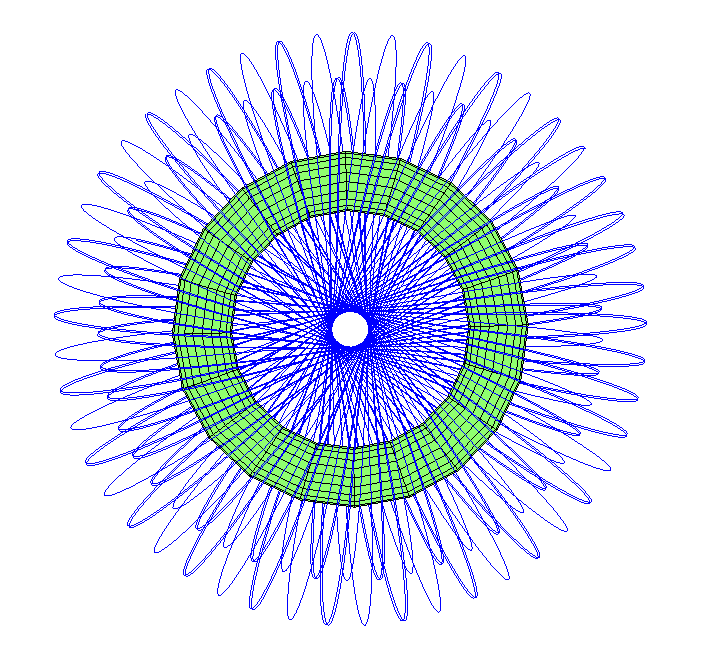
Notez que l'orbite est légèrement allongée. De «l'apogée», au-dessus de l'équateur externe, il passe à travers un trou, apparaît au revers, où il fait l'expérience d'un périgée en un point opposé à celui initial. Ensuite, il passe à nouveau à travers le trou et part à côté de l'endroit où il a commencé à se déplacer - mais la précession le tord le long du tore.

Ces simulations doivent être considérées comme des ébauches principales - les calculs réels nécessitent une plus grande précision. Ma précision numérique n'est pas suffisante pour évaluer la stabilité à long terme. Les champs gravitationnels du Donut et du Hoop semblent encore plus compliqués en raison de leur aplatissement, et le soleil et d'autres planètes y contribueront également.

Forces de marée

Les forces de marée sont un problème. Imaginez une lune se déplaçant autour d'un tore. Un gonflement d'eau et de pierre se forme derrière. Une rotation rapide poussera le gonflement vers l'avant de la lune (si la lune se déplace dans le sens de rotation de la planète et est au-dessus de l'orbite géostationnaire). L'attraction du renflement entraînera elle-même la lune vers l'avant, ce qui lui donnera une accélération - et dans l'espace, cela fait bouger la lune sur une orbite plus élevée. C'est ainsi que la Lune a adopté beaucoup d'élan angulaire de la Terre, a ralenti sa rotation et s'est éloignée d'elle. Dans le cas d'une rotation rapide, comme dans nos tores, l'effet sera plus sensible: les lunes s'éloigneront de la planète et risquent de se perdre.

Qu'arrivera-t-il aux lunes qui sont proches, sous l'orbite géostationnaire? Ils se déplaceront plus vite que les ballonnements, ce qui les ralentira. L'orbite va chuter. Bientôt, ils descendront en spirale et se transformeront en météores géants. La même chose se produira avec les lunes se déplaçant dans la direction opposée. Bien sûr, si la lune est assez grande, les forces de marée peuvent la briser et la transformer en anneau.

Des orbites plus larges passant par le trou risquent de perdre en stabilité. Les orbites du pendule acquerront un élan angulaire en raison d'un gonflement, et la lune se déplacera de plus en plus vite jusqu'à ce qu'elle s'éloigne de la planète ou tombe. Huit orbites peuvent entrer en résonance et gagner et perdre de l'énergie à parts égales, mais un problème similaire les attendra. Donc, très probablement, les tores n'auront pas de lunes vraiment exotiques. Cependant, personne n'interdit de lancer des satellites artificiels avec un support en orbite. Les orbites du pendule peuvent être utiles aux satellites de communication sur la surface intérieure d'un tore.

Résumé

Il est peu probable que les mondes toroïdaux apparaissent naturellement. Mais s'ils le font, ils seront des endroits incroyables pour rechercher l'aventure. Grande surface. Régions aux climats, saisons, gravité et écosystèmes très différents. Magnifique ciel à l'intérieur. Temps effréné. Lune en orbites étranges.

Ce serait bien d'apprendre à les créer non seulement dans des simulations.

Anders Sandberg est chercheur, universitaire, futurologue, transhumaniste et écrivain. Il a obtenu son doctorat en neurobiologie computationnelle de l'Université de Stockholm et est actuellement membre de la James Martin Research Society de l'Université de Future Humanity de l'Université d'Oxford.