Pourquoi le NIF ne s'enflamme-t-il pas?

C'est hohlraum

Le complexe unique de National Ignition Facility - «National Incendiary Equipment» au Lawrence Livermore Laboratory (USA) propose des expériences de fusion thermonucléaire inertielle. Il s'agit du système laser le plus puissant au monde et d'un complexe de laboratoire unique. Tout ce qui concerne les équipements et les solutions techniques mérite les meilleures notes et coûte très cher.

L'endroit où la microexplosion thermonucléaire devrait avoir lieu est appelé le mot allemand hohlraum. Une chambre dorée, qui devrait fournir un chauffage uniforme d'une tablette thermonucléaire avec l'énergie électromagnétique émise par les murs. Quelque chose de similaire avec le même nom et pour le même a une bombe "à hydrogène". Seulement plus gros, et la source de photons est les rayons X de l'explosion nucléaire primaire, pénétrant le hohlraum à travers un canal de rayonnement (interétage).

Grâce à deux entrées, l'intérieur de la chambre en or est éclairé par 192 faisceaux laser ultraviolets d'une puissance totale allant jusqu'à 500 térawatts. En 3 à 5 nanosecondes, 2 à 4 MJ d'énergie y sont reçus, qui doivent être reradiés par les parois dans la gamme des rayons X. Un comprimé thermonucléaire contient 15 microgrammes de deutérium et de tritium à une température de 18 K, ainsi que du gaz injecté dans la cavité interne. La capsule a une coquille sphérique d'un diamètre de 2 mm. Son revêtement ablatif peut être en béryllium ou a une structure composite à base de polyéthylène. Il absorbe jusqu'à 100 KJ d'énergie, entraînant une implosion radioactive de la capsule. La densité de la substance atteint 1 000 g / cm3 et la température du remplissage de deutérium-tritium atteint des centaines de millions de degrés. Après cela, il ne lui reste qu'une chose. Explosez comme une bombe thermonucléaire ou illuminez comme une étoile - comme vous le souhaitez.

Le rendement de microexplosion calculé peut atteindre 20 MJ, ce qui équivaut à 5 kg de TNT. Officiellement, il y aura une fusion thermonucléaire efficace, contrôlée et inertielle. En fait, compte tenu de l'efficacité du système laser ne dépassant pas 1%, une telle technologie ne conduira pas à une source d'énergie pratique. Seuls 420 MJ sont nécessaires pour charger des condensateurs alimentant des amplificateurs laser. Mais le but du NIF n'est pas la production d'électricité, mais la science fondamentale.


Cependant, une réaction éconergétique, c'est-à-dire une «combustion thermonucléaire», échoue obstinément. Bien que la réaction soit de mise. Le New York Times a publié le 6 octobre 2012 une note critique indiquant que le programme du FNI n'a pas atteint ses objectifs déclarés et n'est pas un fait qu'il n'atteindra jamais . Aujourd'hui, nous pouvons déjà conclure que les objectifs du FNI ne sont pas atteints. La fusion thermonucléaire ne brûle pas obstinément, peu importe les astuces des Livermoreites!

On peut supposer pourquoi cela devait se produire. La compression sphérique symétrique de la capsule n'est possible que dans un état d'équilibre thermodynamique. Dans ce cas, la température de surface de la capsule en chaque point est la même, ce qui permet une ablation symétrique. Supposons que les événements de hohlraume se produisent comme les théoriciens du projet NIF l'ont imaginé.

Puis, peu de temps après le début de l'irradiation aux rayons X (nous parlons de fractions de nanosecondes), la surface de la capsule sphérique chauffe jusqu'à des dizaines de millions de K et une couche de plasma ultramince se forme, qui est en (quasi) équilibre avec le rayonnement. Cela signifie que la couche de plasma proche de la surface émet environ la même quantité d'énergie électromagnétique qu'elle reçoit, mais la rayonne également à l'intérieur. Ce dernier conduit au chauffage de la capsule en profondeur et, par conséquent, à un épaississement de la couche de plasma. Lorsque vous vous éloignez de la surface extérieure, sa température diminue jusqu'à ce que le rayonnement vers l'intérieur devienne négligeable. Dans ce cas, le rayonnement vers l'extérieur est d'intensité égale au rayonnement incident sur la capsule, c'est-à-dire l'équilibre viendra. Dans le même temps, la couche de plasma se dilate en raison de la pression, qui est la partie la plus importante du processus d'ablation pour l'implosion.

Il est fondamentalement important que pendant le processus d'ablation, la surface de la capsule soit en (quasi) équilibre thermodynamique avec le rayonnement. Cela nous permet d'estimer la quantité d'énergie entrant dans la capsule en utilisant la loi de Stefan-Boltzmann pour le rayonnement d'un corps complètement noir:

$$

$$I = \ sigma T ^ 4$$

où $$$I$- intensité de rayonnement (W / m2) de la surface ou incident sur la surface chauffée à une température $$$T$Kelvinov $$$\ sigma = 5.67 \ cdot 10 ^ {- 8}$- Constante Stefan-Boltzmann (en SI).

Il en résulte que le rayonnement incident sur la capsule a un spectre de Planck correspondant à la température $$$T$surface de la capsule. Voici à quoi ressemble le spectre quand $$$T = 8 \ cdot 10 ^ 7$K où $$$N (E)$- fraction de photons avec énergie $$$E$dans le nombre total de photons émis par seconde (nous parlons de la distribution de densité du nombre de photons par énergie).


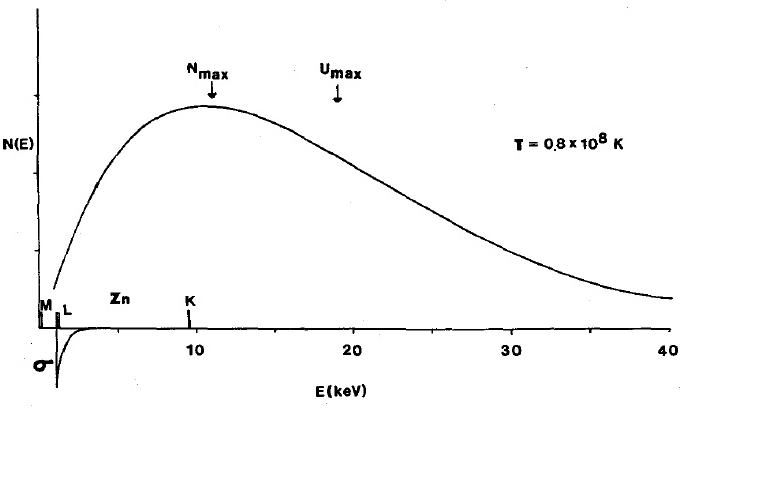
Dans ce spectre, la densité de flux photonique la plus élevée est due à une énergie légèrement supérieure à 10 KeV, ce qui correspond à un rayonnement X avec une longueur d'onde d'environ 1 angström. Il s'agit d'un spectre de rayonnement typique dans la zone de diffusion du rayonnement lors de l'explosion d'une bombe nucléaire (environ 0,5 microsecondes après le début d'une réaction en chaîne, à environ un mètre du point zéro, il n'y a toujours pas d'éclair aveuglant).

Mais d'où viennent les photons d'un spectre de Planck aussi chaud, arrosant la capsule de l'extérieur? Dans les faisceaux laser, il n'y a presque pas de tels photons. Ils sont émis par des parois en hohlraum chauffées par des méga-faisceaux laser. C'est du moins ce que pensaient les théoriciens du projet NIF.

Cependant, ici, ils sont entrés en conflit avec le concept même de hohlraum, car ce terme désigne une chambre dont les parois internes sont en équilibre avec le rayonnement. Mais le rayonnement laser ultraviolet inférieur (essentiellement optique) incident sur les parois de la chambre ne peut pas être en équilibre thermodynamique avec un rayonnement thermique qui obéit à la loi de Stefan-Boltzmann.

Dans le même temps, une couche de plasma avec une température $$$T$près de 100 millions de K. Le plasma émet et absorbe le rayonnement, comme un corps complètement noir. Par conséquent, le rayonnement absorbé par la couche de plasma près des parois de la chambre a le spectre de Planck à température $$$T$. Mais ce n'est pas le cas, ne serait-ce que parce que le rayonnement incident est laser. De plus (et c'est plus important!) - parmi les photons dans les faisceaux laser, il n'y a pas d'énergie de ~ 10 keV. L'énergie des photons arrivant au hohlraum de l'extérieur est de 3 à 4 000 fois inférieure. Par conséquent, les parois du hohlraum ne peuvent pas être en équilibre avec le rayonnement. Mais l'équilibre (quasi) thermodynamique viendra inévitablement lorsque la couche de plasma sera formée et chauffée, de la même manière que celle décrite ci-dessus pour la capsule. Il y a une contradiction!

Une question raisonnable peut se poser ici: ne suis-je pas en train de me contredire quand, d'une part, je considère la couche de plasma proche de la surface comme thermodynamiquement équilibrée, et d'autre part, j'affirme que sa température baisse en profondeur. Non, je ne contredit pas, car nous parlons de quasi-équilibre. En d'autres termes, une couche de plasma externe suffisamment mince peut être considérée comme un équilibre avec le rayonnement et donc émettant, ainsi que l'absorption d'énergie dans le spectre de Planck. C'est pourquoi j'écris souvent sur le (quasi) équilibre thermodynamique d'une surface avec rayonnement. Quelqu'un peut se demander: pourquoi cette couche mince rayonne dans les deux directions pour autant d'énergie qu'elle reçoit d'un c à un? Y a-t-il une contradiction avec la loi de conservation de l'énergie? Il n'y a pas de contradiction, car cette couche mince reçoit également de l'énergie d'une couche adjacente de plasma plus profonde.


Voici à quoi ressemble le bâtiment du NIF. Presque tout est rempli d'un laser

Ainsi, l'image des événements de la chambre d'or, dessinée par l'imagination des théoriciens de Livermore, ne correspond pas à la réalité. Où ont-ils pu obtenir de cette manière, il est possible d'organiser dans le hohlraum quelque chose de similaire à ce qui se passe dans une bombe thermonucléaire, où en aucun cas des photons optiques, mais des rayons X provenant de l'explosion du premier étage arrosent le second ?

Ils l'ont tiré d'expériences réussies sur la génération de rayons X au laser dans une feuille mince éclairée par un laser optique robuste, et d'autres de ce type, qui ont été menées à bien dans les années 90. Mais, apparemment, il n'y avait pas de rayonnement de corps noir correspondant à une température d'environ 100 millions de K, et le plasma dans son ensemble ne s'est pas réchauffé à une telle température. En d'autres termes, ces processus étaient thermodynamiquement hors d'équilibre. Il est à noter que l'énergie laser, qui a été observée dans ce cas, était négligeable par rapport à l'énergie de chauffage.

C'est pourquoi, malgré la concentration d'énergie colossale et apparemment suffisante, la fusion thermonucléaire "ne brûle pas", bien qu'une réaction se produise (la fusion est en principe possible même à température ambiante, car la queue de la distribution de Maxwell approche du zéro absolu, c'est juste détecter cette réaction a peu de chances de réussir). Apparemment, en utilisant le NIF, en principe, il est impossible d'obtenir un chauffage uniforme de la capsule à une température suffisamment élevée, comme c'est le cas dans une bombe thermonucléaire.

Mais que se passe-t-il dans ce cas? Où va l'énergie des faisceaux laser, qui aurait théoriquement dû chauffer la substance de la capsule à 100 millions de K? On peut supposer que la capsule se dilate prématurément et la mélange avec du plasma d'or. Ou en mélangeant du deutérium et du tritium avec la substance de la capsule. En conséquence, même si la température dans le hohlraum atteint les valeurs souhaitées, la pression nécessaire à la synthèse dans la zone de réaction est absente. Mais peut-être quelque chose d'autre est plus important: l'équilibre thermodynamique des parois de la chambre et de la surface de la capsule avec le rayonnement n'est pas atteint, ce qui conduit à un chauffage inégal. L'implosion sphérique ne fonctionne pas!

Comme le montre le raisonnement précédent, pour que la fusion thermonucléaire inertielle fonctionne, il est nécessaire d'irradier la capsule avec des photons à rayons X. Autrement dit, vous devez reproduire en miniature. mécanisme d'implosion par rayonnement utilisé dans une bombe thermonucléaire. Une source de rayons X d'intensité suffisante est un hypothétique laser à rayons X pompé par explosion nucléaire. Comme des photons d'une énergie de ~ 10 keV sont nécessaires, la puissance de l'explosion de la pompe doit être de centaines de kilotonnes ou, éventuellement, de mégatonnes. Bien sûr, l'idée est de mettre le feu à la synthèse dans un volume de ~ 1 cc. mm en utilisant une explosion dans une mégatonne est absurde.

Aujourd'hui, des expériences sont menées avec des lasers à rayons X à électrons libres. Pour générer à une longueur d'onde de 1 angström, ils doivent être couplés à de grands accélérateurs d'électrons. Ce n'est pas moins une structure cyclopéenne que NIF. Mais peut-être que de cette façon, il se révélera allumer une bombe thermonucléaire ou une étoile miniature - comme vous le souhaitez. Bien que les rayons X soient très mal réfléchis, il sera très difficile de les focaliser.

Remarques finales.

1. Le quasi-équilibre est l'état instantané d'un processus sans équilibre, qui peut être considéré comme un équilibre avec une erreur négligeable.
2. La proposition d'utiliser un laser à rayons X pour chauffer un comprimé thermonucléaire ne contredit pas l'affirmation selon laquelle le rayonnement incident sur les parois de la capsule devrait avoir le spectre de Planck. Il aura approximativement un tel spectre en raison de la diffusion inélastique de photons de rayons X sur les parois du hohlraum.
3. Certes, dans mon raisonnement, vous pouvez trouver de nombreuses inexactitudes formelles. Ce n'est pas encore un article scientifique, mais un article scientifique populaire. Mais encore, il me semble que l'essence du principal problème NIF dans cet article se reflète correctement.
4. En particulier, si le NIF est censé irradier la capsule non pas avec des rayons X mais avec des photons doux (ou ultraviolets durs) à une température de plusieurs millions de K (c'est-à-dire loin de 100), alors dans ce cas, les arguments ci-dessus contre le NIF restent valables. A savoir: le spectre d'émission de Planck des parois de hohlraum avec un pic de ~ 1 KeV ou même ~ 0,1 KeV ne peut pas avoir lieu dans le spectre d'absorption laser avec des photons de ~ 1 eV, si un équilibre (quasi) thermodynamique se produit. Si cela ne se produit pas, alors l'implosion à symétrie sphérique est impossible.