L'univers n'a pas commencé avec le Big Bang, mais avec le Big Thaw

Constante cosmologique et création de l'Univers

En ce qui concerne l'Univers, il y a deux énigmes non résolues particulièrement douloureuses, dont l'une est liée à son destin final et la seconde - au début, intrigue les cosmologistes depuis des décennies. La communauté scientifique a toujours cru que ces deux tâches étaient indépendantes l'une de l'autre - mais que faire si ce n'est pas le cas?

La première tâche est liée à l'existence de quelque chose appelé «énergie noire», qui accélère aujourd'hui l'expansion de l'Univers et détermine finalement son sort ultime. Les théoriciens disent que l’action de l’énergie noire peut s’expliquer en introduisant un nouveau terme dans les équations d’Einstein appelé «constante cosmologique». Mais pour que cette explication fonctionne, la constante cosmologique doit avoir une certaine valeur, très petite. En unités naturelles, il est déterminé par une unité divisée par un nombre composé de 123 chiffres! Une explication de la valeur de cette constante est l'un des problèmes les plus difficiles de la physique théorique.


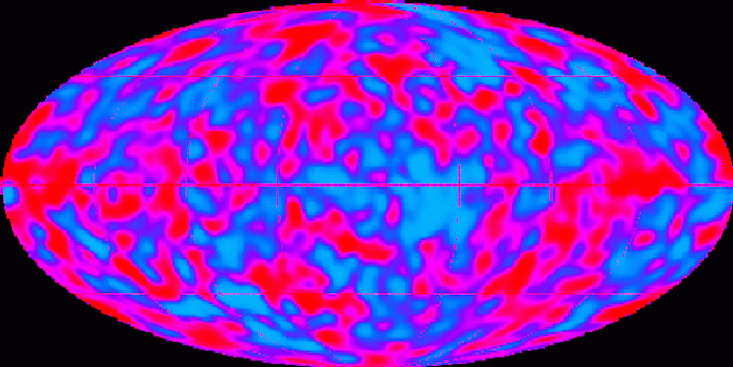Les variations du CMB indiquent des fluctuations de densité dans l'Univers ancien

Le deuxième problème est associé à un autre nombre important qui définit notre Univers et à la formation de structures telles que des galaxies et des groupes de galaxies. Nous savons que l'Univers primitif, bien qu'il soit très homogène, contenait de petites fluctuations de densité, qui sont devenues les causes profondes des structures cosmiques que nous voyons aujourd'hui. Pour coïncider avec nos observations, ces fluctuations devaient avoir une certaine taille et une certaine forme. Comment ces fluctuations sont apparues dans les premières périodes de l'évolution de l'Univers, et leur forme et leur taille, est un mystère tout aussi étonnant de la cosmologie.

Compte tenu de l'approche généralement acceptée de la cosmologie, ces deux nombres - l'ampleur de la constante cosmologique et l'ampleur des perturbations initiales - ne sont pas considérés comme liés. Après tout, l'un d'eux traite de la première phase de l'univers, et le second de la dernière, et ils sont séparés par un temps cosmique de 14 milliards d'années. De plus, la cosmologie standard n'explique pas ces valeurs sur la base de principes fondamentaux. Les modèles universellement acceptés de l'Univers ne disent rien sur la valeur numérique de la constante cosmologique, ou prédisent des valeurs complètement différentes. En ce qui concerne l'ampleur des perturbations initiales, l'approche la plus populaire consiste à obtenir cette valeur à partir de la classe de modèles décrivant l'inflation - une période de croissance rapide au début de l'existence de l'Univers. Le problème avec les modèles inflationnistes est qu'ils peuvent être ajustés pour produire presque n'importe quel résultat, c'est pourquoi ils n'ont pas de capacité prédictive.

Dans mes travaux récents, menés avec ma fille, Hamsa Padmanabhan et Tomalla Fellou à l'École technique supérieure de Zurich, ces deux nombres sont associés à la cosmogenèse - la création de l'Univers - et leur signification exacte est expliquée. Nos travaux, récemment publiés dans Physics Letters B, montrent que l'existence même d'une constante cosmologique, ainsi que sa minuscule valeur, peuvent être représentées comme une conséquence directe du contenu informationnel de l'espace-temps [Padmanabhan, T. & Padmanabhan, H. Cosmic information, the cosmological constante et l'amplitude des perturbations primordiales. Physics Letters B 773, 81-85 (2017)]. De plus, l'analyse fournit la valeur correcte pour la taille et la forme des petites fluctuations de l'Univers primitif.

L'interconnexion remarquable de ces constantes fondamentales est essentielle à notre compréhension de l'univers. En particulier, cela change notre compréhension du Big Bang et élimine le besoin d'une période d'inflation aux premiers stades de l'univers.

Le Big Bang est probablement la caractéristique la plus célèbre de la cosmologie standard. Mais il n'est pas non plus vraiment nécessaire pour elle. Le modèle classique de l'Univers, décrit par les équations d'Einstein, cesse de fonctionner dans les conditions du Big Bang, à une densité et une température infinies - c'est la situation que les physiciens appellent une singularité.

Mais que faire s'il n'y avait pas de singularité? Depuis les années 1960, les physiciens ont travaillé pour décrire l'Univers sans le Big Bang, essayant de combiner la théorie de la gravité et la théorie quantique en quelque chose appelé «gravité quantique». Les physiciens John Wheeler et Bryce DeWitt ont été les premiers à appliquer ces idées à la phase dogométrique hypothétique de l'Univers, dans laquelle les concepts d'espace et de temps n'ont pas encore émergé d'une structure inconnue. Cela a conduit à l'émergence de la cosmologie quantique, dans laquelle les physiciens tentent de décrire la dynamique de modèles jouets simples de l'univers en langage quantique. Inutile de dire qu'au fil des décennies, plusieurs idées différentes, quoique liées, pour décrire la phase pré-géométrique sont soudainement apparues. Ce qui les unit, c'est que l'Univers classique sans aucune singularité apparaît à travers une série de transformations de la phase pré-géométrique à celle dans laquelle l'espace-temps est décrit par les équations d'Einstein. La principale difficulté à construire une telle description est que nous n'avons pas de théorie complète de la gravité quantique qui nous permettrait de modéliser la phase pré-géométrique en détail.


Einstein a appelé sa dépendance à la constante cosmologique plusieurs fois une erreur grossière dans ses équations. Aujourd'hui, les physiciens pensent que cela a une signification positive.

L'ingrédient clé que nous avons introduit pour contourner cette complexité technique est le concept d'information spatiale. Récemment, l'idée que l'information devrait jouer un rôle clé dans la description de la physique gagne de plus en plus de soutien. Il apparaît dans plusieurs cas lorsque les scientifiques tentent de combiner les principes de la théorie quantique et de la gravité - par exemple, dans l'étude des trous noirs quantiques. De plus, dans certains de ces modèles, il existe une idée intrigante de l'holographie, selon laquelle le contenu informationnel d'une grande région peut être lié au contenu informationnel de ses frontières. Mais, malheureusement, la description mathématique des informations dans les différents cas est différente et le principe unificateur, applicable dans tous les cas, n'a pas encore été trouvé. Par conséquent, pour appliquer l'idée de l'information à l'Univers entier, nous avons d'abord dû trouver une définition physiquement appropriée.

La définition des informations spatiales que nous utilisons peut être décrite par analogie. Lorsqu'un morceau de glace fond et se transforme en eau, il y a une transition de phase du solide au liquide. Les processus de transition de phase réels peuvent être extrêmement complexes, mais le nombre total d'atomes de glace sera le même que le nombre d'atomes d'eau. Ce nombre détermine le nombre de degrés de liberté du système qui ne change pas pendant la transition de phase. De la même manière, la transition de phase qui a conduit à l'apparition de l'Univers peut être décrite par un nombre reliant le nombre de degrés de liberté dans la phase pré-géométrique à la quantité inhérente à l'espace-temps classique. En utilisant ce nombre, que nous avons appelé CosmIn, nous pouvons combiner les deux phases de l'univers et contourner les complexités du modèle complet de gravité quantique.

Cosmin, en tant que nombre physiquement observable, doit être fini. En l'absence de singularités, nous pensons que toutes les grandeurs physiques doivent être finies. De plus, nous avons pu montrer que la cosmin ne sera finie que si l'Univers connaît une phase d'expansion accélérée à la fin de la période d'existence - comme nous l'observons aujourd'hui. Cette connexion indique non seulement l'existence d'une raison fondamentale à l'existence d'une constante cosmologique, mais aussi les méthodes de calcul de sa valeur numérique - si nous connaissons la valeur du cosmin.

La valeur de la cosmin dans la phase pré-géométrique ou gravitationnelle quantique de l'Univers peut être déterminée en utilisant les résultats qui apparaissent périodiquement dans différents modèles de gravité quantique. Il s'avère que la quantité totale d'informations transférées de la phase gravitationnelle quantique à la phase classique doit être égale à un nombre simple: 4π, l'aire d'une sphère de rayon unitaire. En utilisant ce fait, nous pouvons relier la valeur numérique de la constante cosmologique à l'échelle d'énergie, sur laquelle l'Univers est passé de la phase de gravitation quantique à la phase classique.

Cette échelle d'énergie de la transition peut être associée à la deuxième propriété mystérieuse de notre Univers: l'ampleur des minuscules fluctuations quantiques dans l'Univers primitif qui ont grandi et formé les galaxies et les amas galactiques que nous voyons aujourd'hui. Un système populaire pour calculer la taille de ces fluctuations utilise des modèles inflationnistes de l'Univers qui décrivent l'Univers traversant une expansion de taille incroyablement grande et rapide. Mais il existe de nombreux modèles inflationnistes et ils sont très différents, et ils peuvent donner la valeur souhaitée. Il convient également de noter que la forme des fluctuations initiales a été obtenue par Edward Robert Harrison en 1970 (et indépendamment par Jacob Zeldovich) et s'appelle le spectre Harrison-Zeldovich. Mais les gens oublient de souligner que Harrison a obtenu son résultat plus de dix ans plus tôt avant l'invention des modèles inflationnistes!

Notre modèle nous permet de relier les deux quantités - la valeur de la constante cosmologique et la taille des fluctuations initiales - avec l'échelle d'énergie à laquelle l'Univers pré-géométrique a connu une transition de phase et est devenu l'Univers classique dans lequel nous vivons. Et, attention, lorsque nous sélectionnons l'échelle d'énergie correcte, nous obtenons la valeur observée correcte pour ces deux valeurs. Cela nous conduit à une relation algébrique entre la constante cosmologique, l'ampleur des fluctuations initiales et le cosmique. Nous pouvons inverser cette relation en utilisant les paramètres cosmologiques observés et vérifier si la valeur de cosmin est vraiment 4π. La théorie réussit parfaitement le test; nous constatons que la cosmin déterminée à partir des observations est 4π avec une précision de 1/1000.

Étonnamment, une combinaison complexe de paramètres cosmologiques, considérés comme indépendants les uns des autres, a une signification si simple. Une approche courante consisterait à considérer une telle relation comme une coïncidence aléatoire. Nous croyons qu'elle nous dit quelque chose de profond et de beau dans notre univers.

Nous pensons que nous avons fait la première tentative pour relier la valeur numérique de la constante cosmologique à la taille des fluctuations dans l'Univers ancien, et pour obtenir ces deux valeurs à partir d'un modèle qui n'a pas de paramètres ajustables et les associe à l'échelle d'énergie sur laquelle l'Univers a commencé à exister.

Toutes ces idées existent sur une plate-forme plus générale de gravité quantique, une théorie que les physiciens, malgré près de cinq décennies de développement, n'ont toujours pas. L'un des avantages de notre modèle est qu'il ne nécessite pas les détails de la gravité quantique. Mais elle fait deux indices importants sur la nature de la gravité quantique et la structure de l'espace-temps. Premièrement, elle dit que l'espace-temps doit être représenté comme composé de degrés de liberté microscopiques, ainsi que de matière constituée d'atomes. Deuxièmement, elle soutient que la théorie correcte de l'origine de l'univers devrait inclure une transition de phase de la phase pré-géométrique à la phase classique.

Ces conseils peuvent répondre à une question clé: pourquoi, après plusieurs décennies de travail, les théoriciens n'ont pas combiné la gravité et la théorie quantique? Nous pensons que cela s'explique mieux par une autre analogie. Nous savons que la dynamique des fluides est une théorie physique cohérente exprimée à travers un ensemble d'équations. Si nous les prenons comme fondamentaux et leur appliquons les principes de la théorie quantique, nous pouvons découvrir un nouveau phénomène intéressant - par exemple, les phonons (quanta de vibration) et leurs interactions. Cependant, en utilisant cette approche, nous ne pourrons pas arriver à la structure quantique de la matière.

Il existe des preuves que les équations décrivant la gravité dans ce sens sont similaires à la dynamique des fluides. En d'autres termes, reformuler les équations décrivant la gravité en utilisant les principes de la théorie quantique est similaire à l'application des principes quantiques aux équations de la dynamique des fluides. Nous ne découvrirons pas la structure quantique de l'espace-temps de cette manière - et nous pensons qu'en raison de cette décennie, les tentatives de quantification de la théorie d'Einstein se sont soldées par un échec bruyant.

Au lieu de cela, nous devons repenser la nature de la gravité et comprendre ce qu'elle nous apprend sur la structure microscopique de l'espace-temps. Le physicien Ludwig Boltzmann a utilisé cette approche pour comprendre que les phénomènes de température nécessitent la notion de matière comme consistant en degrés de liberté discrets (en d'autres termes, des atomes). Boltzmann, en fait, a déclaré que si quelque chose peut être chaud, il devrait contenir des degrés de liberté microscopiques.

L'espace-temps peut aussi avoir une température et sembler chaud à certains observateurs. Cette idée est née grâce au travail de Jacob Beckenstein et Stephen Hawking dans le contexte des trous noirs. Peu de temps après, au milieu des années 70, les travaux de Bill Unrich et Paul Davis ont montré que c'est la principale propriété de l'espace-temps. En combinant le paradigme de Boltzmann avec le fait que l'espace-temps - comme la matière ordinaire - peut être chaud, vous arrivez à la conclusion que l'espace-temps doit avoir des degrés de liberté internes, comme les atomes dans la matière. Des preuves théoriques à l'appui de cette conclusion ont commencé à émerger ces dernières années [Padmanabhan, T. Les atomes de l'espace-temps et la constante cosmologique. Journal of Physics: Conference Series 880, 012008 (2017)]. Cette observation contient la clé pour comprendre la microstructure de l'espace-temps, qui conduit rapidement à des résultats remarquables.

Tout d'abord, l'évolution d'un site spatio-temporel peut être décrite en termes de degrés de liberté (ou, de manière équivalente, de contenu informationnel) situés à l'intérieur des limites de ce site. Deuxièmement, la gravité devient insensible aux changements à un niveau d'énergie nul. Dans la théorie d'Einstein, la gravité est responsable de la quantité absolue d'énergie, c'est pourquoi il est presque impossible de calculer la constante cosmologique. Mais pour un paradigme basé sur le contenu de l'information, ce n'est pas le cas. Troisièmement, l'approche informationnelle suggère qu'il ne faut pas imaginer l'évolution cosmique selon une certaine solution des équations d'Einstein. Ces équations proviennent d'un ensemble plus précis d'équations décrivant les degrés quantiques de liberté de l'espace-temps [Padmanabhan, T. Comprenons-nous vraiment le Cosmos? Comptes Rendus Physique 18, 275-291 (2017)].

L'approche informationnelle, confirmée par notre modèle cosmique, nous donne une nouvelle image vivante de l'Univers, semblable à un gros morceau de glace contenant une source de chaleur. Une source de chaleur fait fondre la glace autour d'elle, créant une section d'eau qui se dilate, atteignant l'équilibre thermodynamique local. À grande échelle, plus près de la limite de phase, les molécules n'ont pas encore atteint l'équilibre, car un morceau de glace est chauffé de l'intérieur. Fait intéressant, cela est très similaire au comportement de notre univers. Une parcelle d'eau est similaire à l'Univers observable (décrit par la théorie d'Einstein). Il est entouré d'une phase pré-géométrique (semblable à la glace), décrite par des lois inconnues jusqu'à présent de la gravité quantique. L'idée du Big Bang disparaît, et au lieu de cela une transition apparaît d'une phase à l'autre le long de leur frontière. La nécessité d'une période d'inflation disparaît également.

L'ensemble de la plateforme est simple et élégant, car il est décrit par un seul paramètre: l'échelle d'énergie de la transition de phase de l'Univers primitif de la pré-géométrie à la géométrie d'Einstein. Cela diffère des modèles inflationnistes classiques qui contiennent de nombreux paramètres et n'ont pas de capacités prédictives. Notre modèle n'utilise pas de physique non vérifiée. Le seul postulat que nous avons fait est que le contenu de l'Univers doit être égal à 4π, la surface d'une seule sphère.

Le travail ouvre trois nouveaux domaines de recherche. Elle nous invite tout d'abord à étudier la physique de la phase pré-géométrique dans différents modèles de gravité quantique. Deuxièmement, il donne l'occasion d'étudier l'idée de l'information spatiale utilisée dans ce travail et d'essayer de la relier à d'autres idées similaires utilisées dans d'autres contextes. Troisièmement, il renforce l'idée que l'espace-temps se compose de degrés de liberté plus élémentaires - tout comme la matière est constituée d'atomes - et nous encourage à étudier les différentes phases de l'espace-temps de la même manière que nous étudions les différentes phases de la matière en physique de la matière condensée .

Tanu Padmanabhan est professeur au Centre interuniversitaire d'astronomie et d'astrophysique de l'Inde.