Demandez à Ethan: Quelle est la différence entre les fermions et les bosons?

Particules du modèle standard, avec les masses indiquées dans le coin supérieur gauche. Trois colonnes de gauche sont occupées par des fermions, deux colonnes de droite sont des bosons

Dans tout l'univers, il n'y a que deux types de particules fondamentales: les fermions et les bosons. Chaque particule, en plus des propriétés habituelles que vous connaissez, telles que la masse et la charge électrique, a sa quantité inhérente de moment angulaire, connue sous le nom de spin. Les particules à spins demi-entiers (± 1/2, ± 3/2, ± 5/2, ..) sont appelées fermions. Les particules à spins entiers (0, ± 1, ± 2, ..) sont des bosons. Il n'y a pas d'autres particules, fondamentales ou composites, dans l'Univers. Mais pourquoi est-ce important? Notre lecteur demande:

Pourriez-vous expliquer la différence entre fermions et bosons? Qu'est-ce qui change lorsque l'on passe d'un spin entier à un demi-entier?

À première vue, la division des particules en catégories par de telles propriétés semble aléatoire.


Particules connues dans le modèle standard. Ce sont toutes des particules fondamentales, découvertes directement. À un graviton, alors qu'il n'est pas encore découvert, le spin sera égal à 2.

Après tout, une particule est une particule, n'est-ce pas? Bien sûr, il y a plus de différence entre les quarks (soumis à une forte interaction) et les leptons (non soumis à celle-ci) qu'entre les fermions et les bosons? Bien sûr, la différence entre la matière et l'antimatière signifie plus que le spin? La présence ou l'absence de masse est-elle bien plus que quelque chose d'aussi insignifiant que le moment angulaire?

Il s'avère qu'il existe plusieurs petites différences significatives liées au spin, mais il y a deux différences sérieuses qui sont beaucoup plus importantes que la plupart des gens ne le pensent, et même la plupart des physiciens.


Photons, particules et antiparticules dans l'Univers primitif. Il était rempli de bosons et de fermions, ainsi que de tous les antifermions imaginables

Premièrement, seuls les fermions ont des copies parmi les antiparticules. Antiparticule pour quark - antiquark. L'antiparticule d'un électron est un positron, tandis qu'un neutrino a un antineutrino. Les bosons, d'autre part, sont des antiparticules d'autres bosons, et de nombreux bosons sont des antiparticules d'eux-mêmes. Il n'y a pas d'antiboson. Collider un photon avec un autre photon? Z ⁰ avec un autre Z ⁰ ? C'est la même chose, en termes d'interaction de la matière et de l'antimatière, que l'annihilation d'un électron et d'un positron.


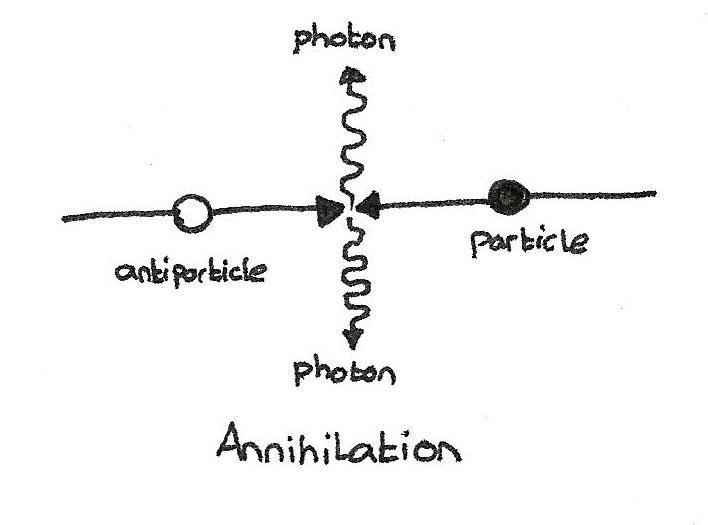Un boson - comme, par exemple, un photon - peut être une antiparticule pour lui-même, mais les fermions et les antifermions sont différents (comme un électron et un positron)

Des particules composites peuvent être créées à partir de fermions: deux quarks supérieurs et un inférieur donnent un proton (fermion), un supérieur et deux inférieurs donnent un neutron (fermion). En raison de la nature du spin, si vous prenez un nombre impair de fermions et les liez ensemble, la nouvelle particule composite se comportera comme un fermion. C'est pourquoi les protons et les antiprotons existent, et donc le neutron est différent de l'antineutron. Et les particules composées d'un nombre pair de fermions, comme une combinaison quark-antiquark (connue sous le nom de méson), se comportent comme un boson. Le pion neutre π ⁰ est lui-même une antiparticule.

La raison est simple: chacun de ces fermions est une particule avec un spin de ± 1/2. Si vous ajoutez deux particules ensemble, vous obtenez un objet avec une rotation de -1, 0 ou +1, c'est-à-dire un entier (et donc, c'est un boson). Si vous en ajoutez trois, vous obtenez une rotation de -3/2, -1/2, +1/2 ou +3/2, c'est-à-dire un fermion. La différence de particules et d'antiparticules est donc assez grande. Mais il y a une deuxième différence, peut-être encore plus importante.


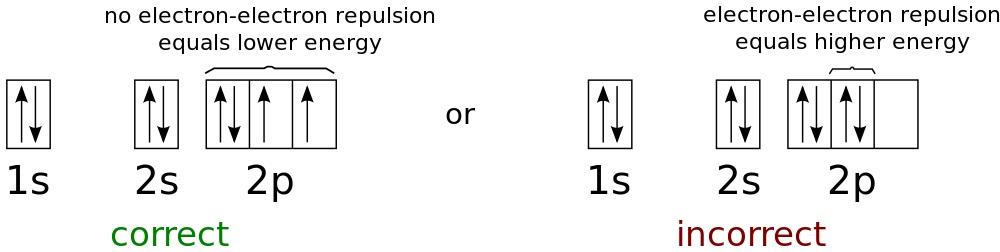Niveaux d'énergie pour les énergies les plus faibles possibles dans un atome d'oxygène neutre. Puisque les électrons sont des fermions, pas des bosons, ils ne peuvent pas tous exister au premier niveau, même à des températures arbitrairement basses

Le principe d'interdiction de Pauli ne s'applique qu'aux fermions et non aux bosons. Il postule que dans tout système quantique, deux fermions ne peuvent pas occuper le même état quantique. Les bosons n'ont pas de telles restrictions. Si vous prenez le noyau d'un atome et commencez à y ajouter des électrons, le premier électron entrera dans l'état fondamental - l'état avec l'énergie la plus basse. Comme il s'agit d'une particule avec un spin de 1/2, l'état de son spin peut être +1/2 ou -1/2. Si vous ajoutez un second électron à l'atome, son spin sera dans l'état opposé, et il entrera également dans l'état avec l'énergie la plus basse. Mais si vous ajoutez plus d'électrons, ils ne pourront pas entrer dans l'état fondamental, et ils devront s'installer au prochain niveau d'énergie.


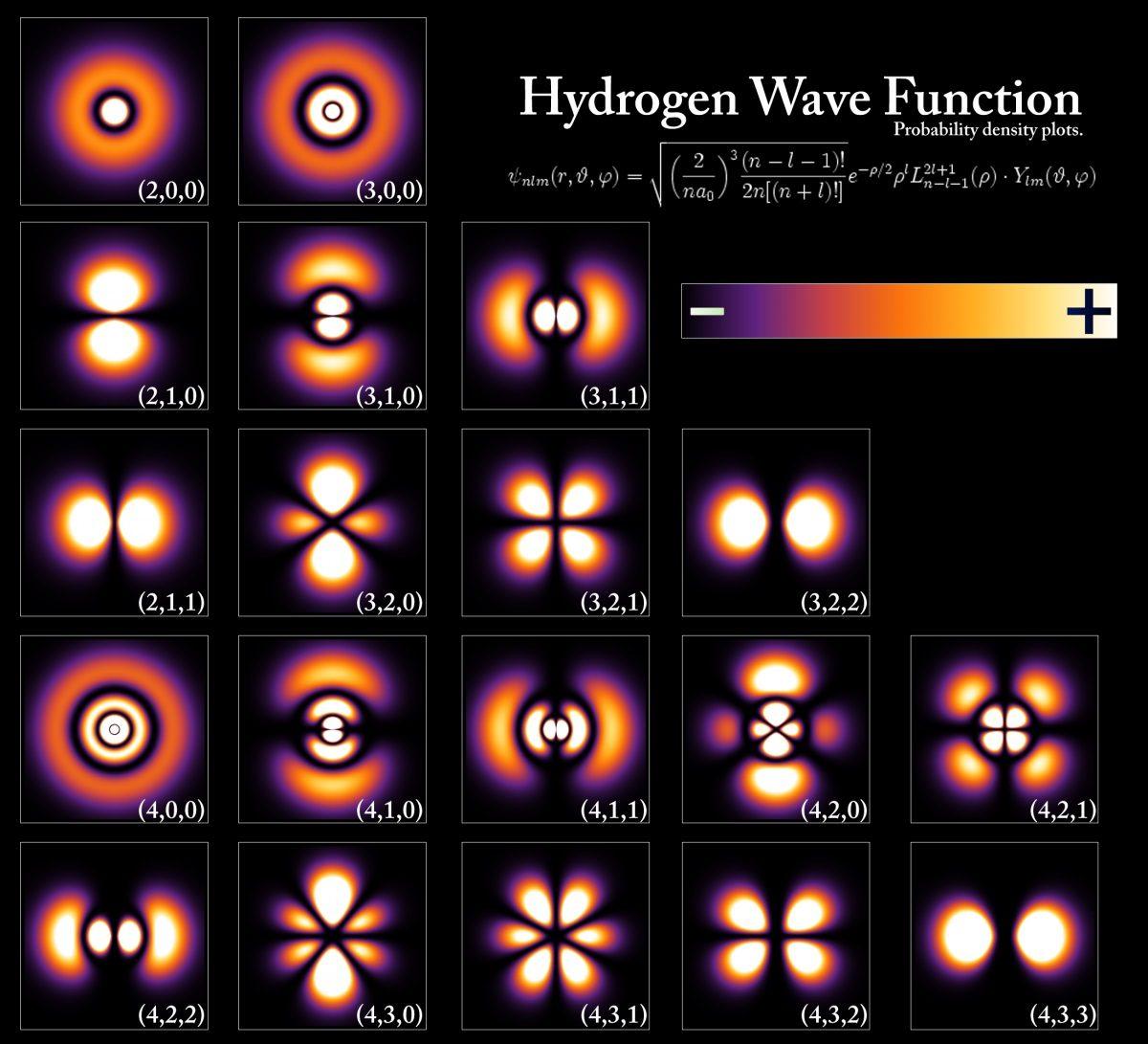Les niveaux d'énergie et les fonctions d'onde des électrons correspondant aux différents états de l'atome d'hydrogène.

C’est pourquoi le système périodique des éléments de Mendeleïev est ainsi organisé. Par conséquent, les atomes ont des propriétés différentes, ils se lient ensemble dans de telles combinaisons complexes, et donc chaque élément du tableau est unique: la configuration des électrons dans chaque atome est différente de toutes les autres. Le fait que deux fermions ne puissent pas être dans le même état quantique conduit à l'apparition de certaines propriétés physiques et chimiques des éléments, à un grand nombre de combinaisons moléculaires et à des liaisons fondamentales en raison desquelles des réactions chimiques complexes et la vie sont possibles.


La façon dont les atomes se lient et forment des molécules, y compris des molécules organiques, n'est possible que grâce au principe d'interdiction de Pauli

D'un autre côté, autant de bosons que vous le souhaitez peuvent être amenés dans le même état quantique! Cela vous permet de créer des états bosoniques spéciaux, appelés condensats de Bose-Einstein. En refroidissant tellement les bosons qu'ils se retrouvent dans un état avec le moins d'énergie, vous pouvez en placer n'importe quel nombre au même endroit. L'hélium (composé d'un nombre pair de fermions, se comportant donc comme un boson) à basse température se transforme en un superfluide - le résultat de la condensation de Bose-Einstein. À ce jour, les gaz, les molécules, les quasi-particules et même les photons ont réussi à amener un tel état. Une recherche active est toujours en cours dans ce domaine.


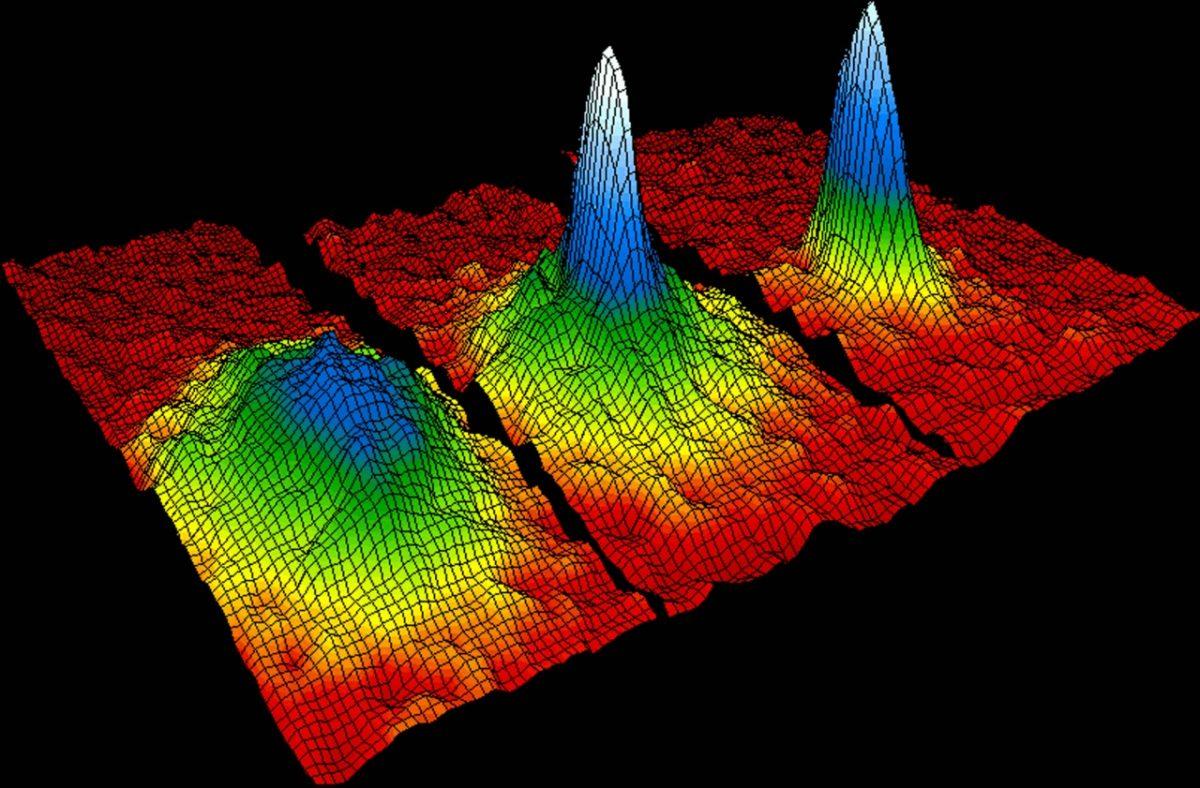Atomes de rubidium avant (à gauche), pendant (au milieu) et après (à droite) la transition vers l'état de condensat de Bose-Einstein. Le graphique montre comment les atomes se condensent de régions rouges, jaunes et vertes moins denses à des zones bleues et blanches plus denses

Le fait que les électrons soient des fermions conduit au fait que les étoiles naines ne s'effondrent pas sous leur propre poids; le fait que les neutrons soient des fermions conduit au fait que l'effondrement des étoiles à neutrons s'arrête à un moment donné. Le principe d'interdiction de Pauli, responsable de la structure atomique, empêche les objets physiques les plus denses de devenir des trous noirs.


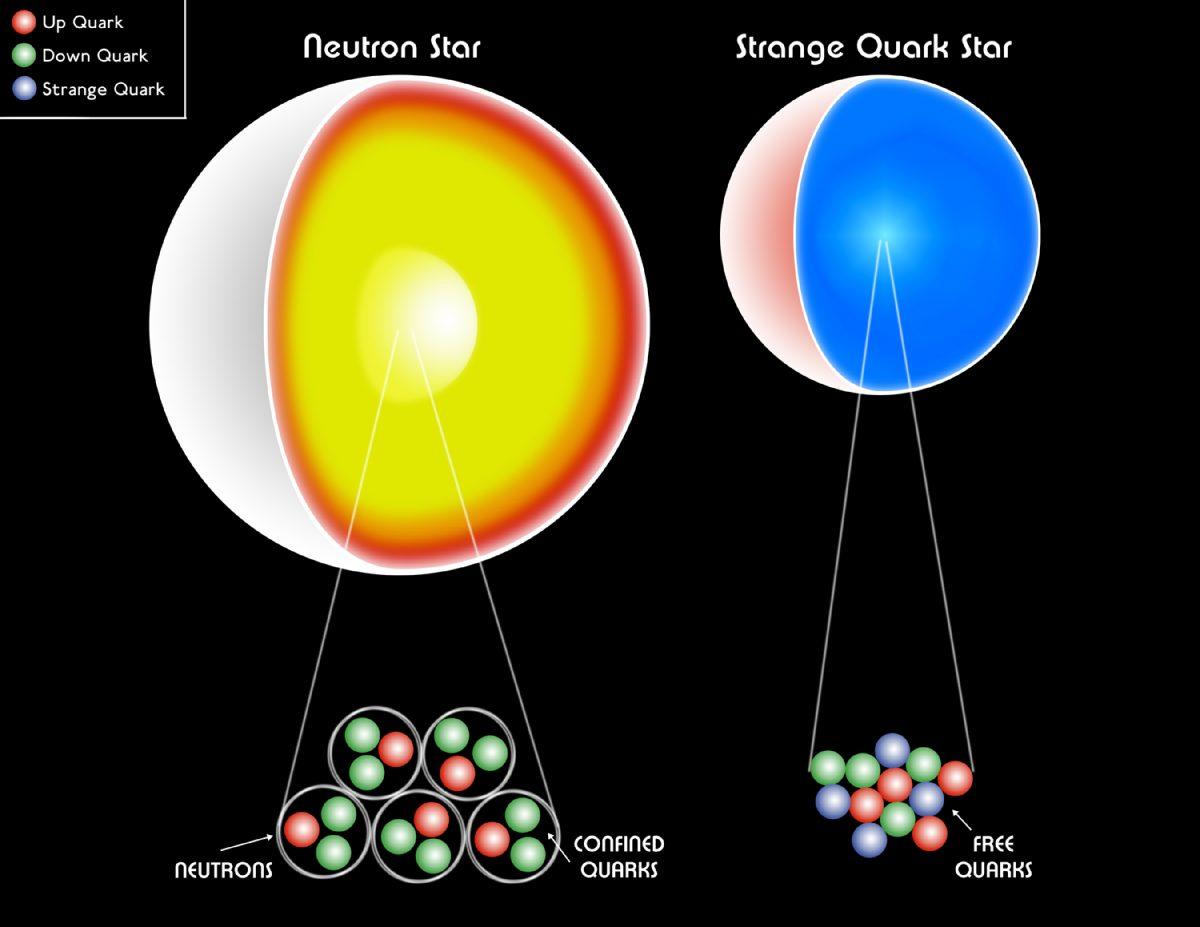La naine blanche, l'étoile à neutrons et même l' étoile de quark sont toutes constituées de fermions.

Lorsque la matière ou l'antimatière s'annihile ou se désintègre, elles chauffent le système à des températures selon que les particules obéissent aux statistiques de Fermi-Dirac (pour les fermions) ou de Bose-Einstein (pour les bosons). Par conséquent, aujourd'hui, la température du rayonnement CMB est de 2,73 K, et le rayonnement de fond des neutrinos est de 0,8 K plus bas: cela était dû à l'annihilation et à ces statistiques, qui ont fonctionné dans l'Univers primitif.


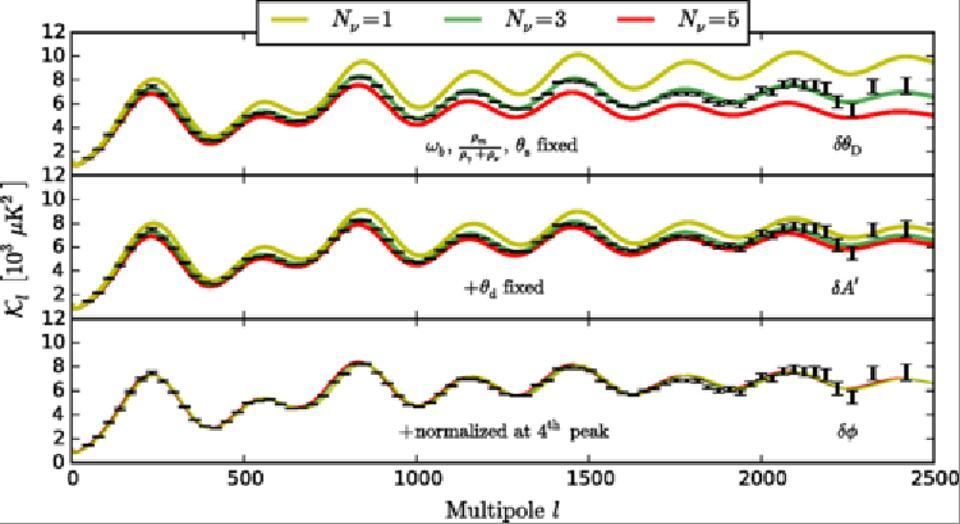Ajuster le nombre de neutrinos pour correspondre aux données sur les fluctuations du CMB. Les données coïncident avec le rayonnement des neutrinos, dont la température équivalente en énergie est de 1,95 K - beaucoup moins que celle des photons CMB

Le fait que le spin soit à moitié intégral dans les fermions et le spin entier dans les bosons est intéressant en soi, mais il est beaucoup plus intéressant que ces deux classes de particules obéissent à des règles quantiques différentes. À un niveau fondamental, ces différences rendent notre existence possible. C'est un bon résultat pour des bagatelles telles que la différence de ± 1/2 dans le moment angulaire interne. Mais les vastes conséquences d'une règle apparemment purement quantique illustrent l'importance du spin et la différence entre les bosons et les fermions.

Ethan Siegel - astrophysicien, vulgarisateur scientifique, auteur de Starts With A Bang! Il a écrit les livres «Beyond the Galaxy» [ Beyond The Galaxy ] et «Tracknology: the science of Star Trek» [ Treknology ].