Lorsque je parle avec une personne éloignée de la physique de possibles dimensions supplémentaires de l'espace qui nous sont inconnues, alors l'une des questions les plus fréquemment posées est: «Comment imaginez-vous des dimensions supplémentaires? Je ne peux en imaginer que trois, et je ne comprends pas comment aller plus loin; cela n'a aucun sens pour moi. "
Ce que nous, les physiciens, ne faisons pas (du moins aucune de mes connaissances n'a prétendu le faire), nous n'imaginons donc pas de dimensions supplémentaires. Mon cerveau est limité comme le vôtre, et bien que ce cerveau crée facilement une image tridimensionnelle du monde dans lequel je peux me déplacer, je ne peux pas le forcer à représenter une image d'un monde à quatre ou cinq dimensions, tout comme vous. Ma survie ne dépendait pas de la capacité d'imaginer quelque chose comme ça, il n'est donc peut-être pas surprenant que mon cerveau ne soit pas à l'écoute.
Au lieu de cela, je (et à en juger par notre échange d'idées, la plupart de mes collègues aussi) développe une intuition basée sur une combinaison d'analogies, d'astuces de visualisation et de calculs. Nous omettons les calculs ici, mais de nombreuses analogies et astuces ne sont pas si difficiles à expliquer.
Les réflexions sur les dimensions supplémentaires peuvent être apprises en deux étapes.
- Une étape simple consiste à apprendre à imaginer ou à décrire le monde avec des dimensions supplémentaires. Vous connaissez déjà plusieurs façons de procéder, même si vous n'en êtes pas conscient - et vous pouvez en apprendre un peu plus.
- L'étape la plus difficile est d'apprendre comment tout fonctionne dans le monde avec des dimensions supplémentaires. Comment travailler avec une aiguille en quatre dimensions, et non en trois; si les planètes se déplaceront sur des orbites autour du soleil dans six dimensions spatiales; des protons et des atomes se formeront-ils? Ici, vous devrez apprendre des astuces inconnues, représentant les différences entre un monde avec seulement une ou deux dimensions et un monde en trois dimensions que nous connaissons, et travaillant par analogie.
Commençons donc par vous aider à imaginer le monde avec des dimensions supplémentaires. Pour ce faire, vous devez réfléchir à la manière dont nous représentons en général n'importe quelle dimension. Commençons par le début.
- Un monde à zéro dimension est un point. On ne peut pas dire grand-chose de lui maintenant, mais nous reviendrons sur lui.
- Le monde unidimensionnel est déjà assez intéressant.
- Dans les mondes à deux dimensions, des choses beaucoup plus intéressantes se produisent.
- Il est important d'éviter toute confusion entre les dimensions spatiales et la signification plus générale du mot «dimension» dans le langage ordinaire, ainsi qu'en mathématiques et statistiques.
- Et puis divers exemples de dimensions supplémentaires suivront, en mettant l'accent sur ce que signifie exactement «supplémentaires», et comment il se peut que dans notre monde il y ait des dimensions sur lesquelles nous ne savons rien.
- Nous examinerons également comment exactement ces mesures invisibles peuvent être détectées.
Mondes unidimensionnels
Un monde avec une dimension spatiale est beaucoup plus simple qu'un monde avec trois, mais il contient quelque chose qui peut être raisonné. Par exemple, il existe plusieurs types de mondes unidimensionnels. Ils ont non seulement certaines propriétés communes, mais aussi des différences intéressantes.
Pour le premier exemple, considérons la mesure non pas comme un concept physique, mais comme un concept plus général. Cela vous aidera à bien des égards, par exemple en distrayant votre intuition des idées fausses naturelles sur les dimensions et leur fonctionnement. Parlons des gains annuels - combien d'argent une personne reçoit pour une année donnée. C'est une dimension d'étude aussi appropriée que tout le monde.
Mesure des revenus
Votre revenu pour l'année écoulée est un certain nombre dans votre devise locale. Elle peut être positive ou négative, grande ou petite; il peut être représenté comme un point sur une ligne, comme dans la fig. 1, que nous appellerons le «point de revenu». Chaque point de la ligne représente un retour possible.
Fig. 1: une ligne de revenus de longueur infinie, dont le côté gauche représente les pertes, le côté droit représente les revenus.Ce qui fait du revenu annuel une propriété unidimensionnelle est (très grossièrement) ce qui suit:
• La position dans l'espace est indiquée par une unité d'information: dans notre cas, par le revenu.
Notez également qu'il est continu (ou presque continu) - si deux personnes ont des revenus différents A et B, nous pouvons trouver un tiers dont le revenu se situe entre A et B.
Ces deux faits impliquent que le revenu peut changer continuellement le long de la ligne de revenu, se déplaçant vers la droite ou la gauche - vers un revenu supérieur ou inférieur. Il n'y a pas d'autre option.
Bien sûr, la ligne de revenus n'a rien à voir avec l'espace physique dans lequel vous et moi pouvons marcher, mais c'est toujours une dimension. Et (au moins en principe), il n'a de fin dans aucune des parties: il n'y a (en principe) aucune limite sur le montant qu'une personne peut gagner ou perdre en un an. Ce monde unidimensionnel n'est pas si diversifié, mais nous pouvons toujours poser des questions significatives à ce sujet:
- Comment les revenus annuels sont-ils répartis aux États-Unis?
- Quel est le revenu annuel moyen au Japon?
- Comment les réponses à ces questions changent-elles au fil du temps?
Ces questions ont un sens dans le monde unidimensionnel de la ligne de revenus.
Mesure arc-en-ciel
Et voici un autre monde complètement différent. Une seule dimension est formée par les couleurs de l'arc-en-ciel, du rouge, à l'orange, au jaune, de là au vert, [bleu], bleu et violet [Les anglophones ont six couleurs dans un arc-en-ciel, ils n'émettent pas de bleu / env. trad.]. De ce point de vue, les couleurs forment un monde unidimensionnel de taille finie. En dehors du rouge ou du violet, il existe des formes invisibles de fleurs, mais du point de vue de vos yeux, la mesure se termine sur elles. Maintenant, il n'est pas présenté sous la forme d'une ligne infinie, mais sous la forme d'un segment - la «ligne arc-en-ciel» sur la Fig. 2. Veuillez ne pas le confondre avec la roue chromatique - s'il est fermé, notre mesure commence par le rouge et se termine par le violet. Et encore une fois, la position sur la ligne arc-en-ciel est déterminée par une unité d'information (couleur), et elle est continue.
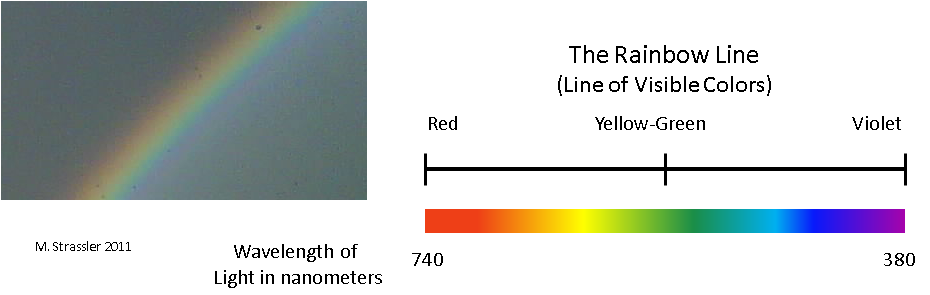Fig. 2Ce n'est évidemment pas non plus une mesure de l'espace physique! Vous pouvez lancer une balle de votre maison à la maison de votre voisin, mais vous ne pouvez pas imaginer comment vous lancez une balle du vert à l'orange - cela n'a aucun sens. Et ce sera toujours aussi une dimension. Ici, vous pouvez poser beaucoup de questions significatives: comment la couleur de la pomme se déplace-t-elle le long de la ligne arc-en-ciel dans le processus de transformation d'une pomme du vert au rouge? Combien au soleil de chacune des fleurs? Si une étoile orange commence à devenir rouge, deviendra-t-elle jaune en premier?
Mesure de la direction du vent
Et voici la troisième option de mesure, et encore une autre. Si vous écoutez les prévisions météorologiques, on vous dira que le vent commencera bientôt à souffler du nord, ou du nord-ouest, ou du sud-ouest. Les directions possibles du vent sont également une mesure. Veuillez noter qu'il ne s'agit pas d'une dimension spatiale! Dans cette dimension, vous ne pouvez pas lancer la balle comme vous la lancez vers le haut, la gauche ou l'avant. Ceci est une mesure des directions dans l'espace!
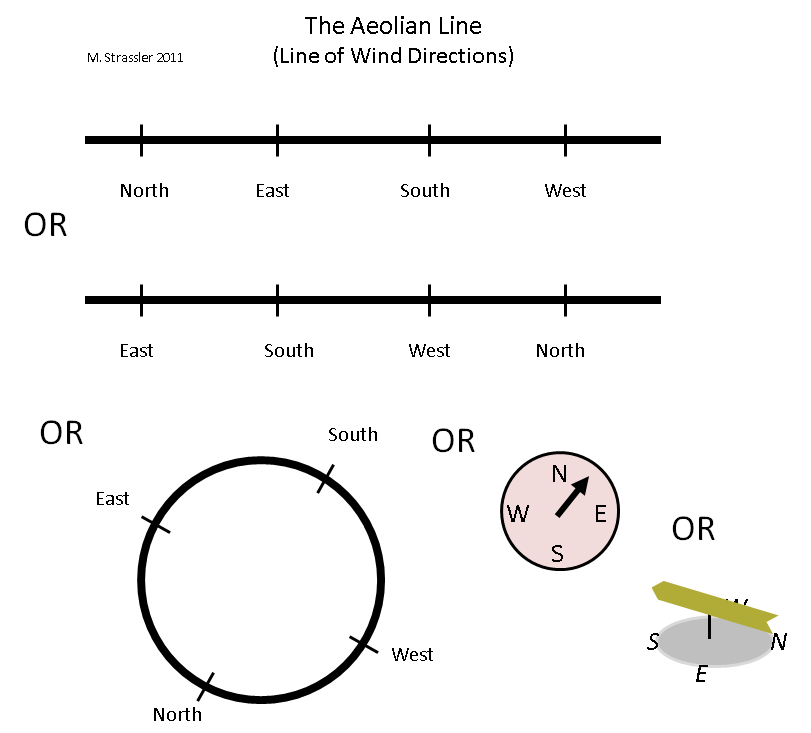Fig. 3Comment représenter cette dimension? Il existe au moins deux méthodes naturelles pour cela, illustrées à la fig. 3. On utilise le segment - la "ligne éolienne" (
Aeolus est un demi-dieu, le souverain des éléments aériens des Grecs anciens) - mais la ligne éolienne diffère de la ligne arc-en-ciel par sa fréquence. La direction du vent peut changer du nord à l'est, puis au sud, puis à l'ouest, puis de nouveau au nord, en continu. Et à notre avis, la ligne peut être coupée n'importe où - comparez les deux lignes en haut de la Fig. 3, qui représentent également la ligne éolienne. L'essentiel, c'est que le vent peut aller de l'extrémité droite de la ligne directement à l'extrémité gauche, et vice versa, donc peu importe où le couper. Ou peut-être que la façon la plus simple de représenter cette ligne périodique est sous la forme d'un cercle. C'est ce que nous faisons avec une boussole ou une girouette!
Trois mondes unidimensionnels différents
Et ici, vous avez des mondes unidimensionnels. Voyez à quel point ils sont riches en détails! Différentes tailles, différentes propriétés. Sur la ligne de revenu, le revenu peut augmenter ou diminuer pour toujours. Sur la ligne arc-en-ciel, vos yeux ne peuvent que passer au violet, ou inversement, uniquement au rouge. Et sur la ligne éolienne, le vent peut faire un cercle complet autant que vous le souhaitez - mais en même temps, il reviendra toujours dans l'une des directions.
Ces variétés de mondes unidimensionnels - infinis, finis et finis-périodiques, représentés par une ligne, un segment et un cercle infinis - sont les ingrédients de base pour comprendre les mondes de dimensions supérieures. Je les contacterai plus d'une fois. Dans la fig. 4 ils sont présentés, ainsi que le quatrième type, s'étendant à l'infini dans une seule direction. Un exemple d'une telle mesure peut être la température: elle peut être arbitrairement grande, mais il y a la température la plus basse possible - zéro absolu - donc la température forme une ligne commençant à zéro absolu et montant à partir de là, mais pas vers le bas.
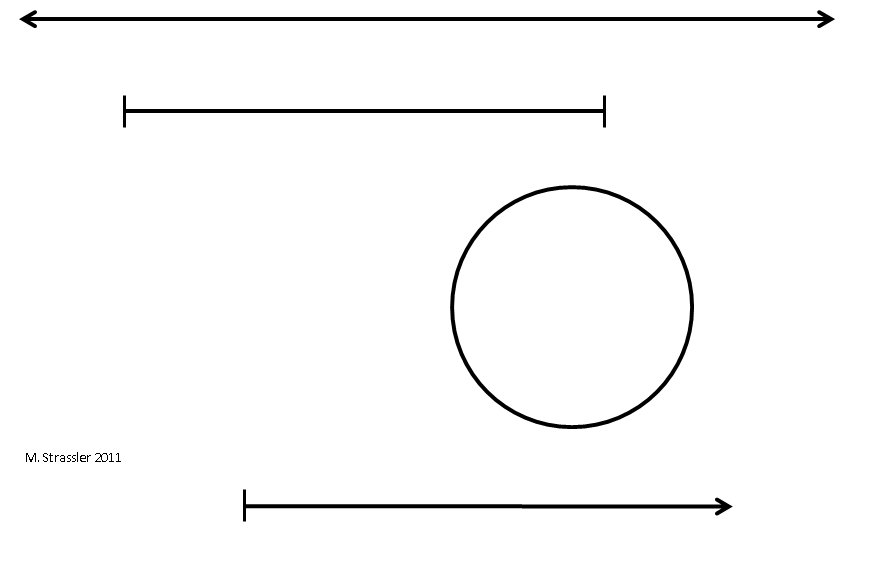Fig. 4Comment représenter les dimensions, l'espace et autres
J'ai mentionné avec désinvolture ou utilisé plusieurs méthodes différentes pour représenter les mesures. Le revenu peut être représenté par un nombre ou une ligne sans fin. L'arc-en-ciel visible peut être représenté comme un segment ou comme une couleur, et peut également utiliser un nombre - la longueur d'onde des photons correspondant à une certaine couleur. La direction du vent peut être représentée par un cercle, ou un segment dont l'extrémité gauche est reliée à la droite - ou des mots comme nord, est, sud, ouest - ou un nombre qui définit la direction en degrés, allant de 0 à 360 et de retour à 0. Ce que nous pouvons présenter une dimension de plusieurs façons différentes nous donne une grande flexibilité pour la formation au travail intuitif avec des dimensions supplémentaires.
Pour illustrer ces types de mesures, j'ai choisi des concepts qui n'ont rien à voir avec l'espace physique - revenu, couleur de l'arc-en-ciel, direction du vent - pour montrer que les mesures spatiales sont des exemples concrets d'un concept de mesure plus général. Comprendre ce fait facilite grandement les tentatives d'imaginer des mondes à plus de trois dimensions. Rappelez-vous, j'ai mentionné deux parties du processus de réflexion sur les dimensions supplémentaires? Tout d'abord, apprenez à les représenter; deuxièmement, comprendre comment tout fonctionne et fonctionne en eux. Les dimensions spatiales ont des caractéristiques associées au fonctionnement de certaines choses, mais pas à leur présentation.
Mondes spatiaux avec une dimension efficace
Compte tenu de tout cela, considérons les mondes spatiaux que nous rencontrons régulièrement avec une dimension efficace. Ou, plus précisément, des situations où un certain aspect de notre monde se comporte comme si l'espace n'avait qu'une seule dimension. Ensuite, nous disons que le monde de certains participants ou objets devient effectivement unidimensionnel.
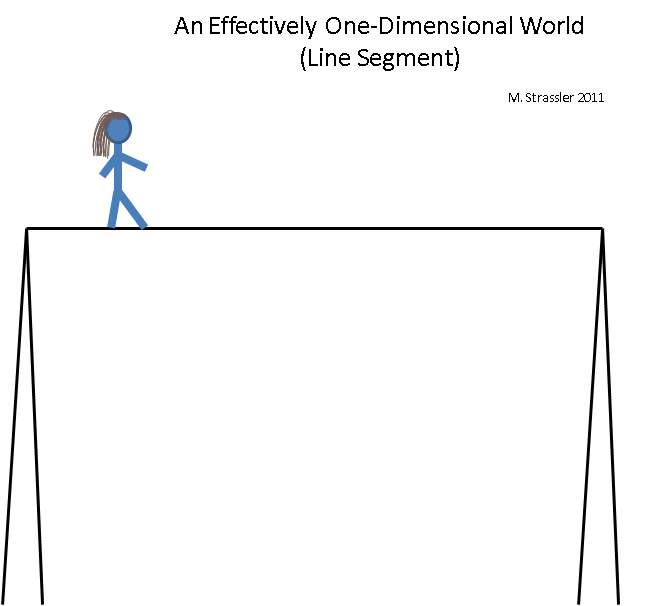Fig. 5Imaginez un funambule en équilibre sur une corde haute. Le monde du funambule est effectivement unidimensionnel (bien que, bien sûr, il reste en fait tridimensionnel), car il ne peut pas se déplacer en toute sécurité dans une autre direction que de droite à gauche ou de gauche à droite. Ce monde est comme un monde arc-en-ciel - il est de longueur finie et lorsque le funambule atteint la fin, il doit se retourner et revenir en arrière (ou descendre de la corde, mettant fin à une situation dans laquelle le monde devient effectivement unidimensionnel). Que puis-je dire d'autre? La position sur la corde peut être déterminée par une unité d'information (par exemple, la distance du pôle gauche au funambule). Deux funambules peuvent se rencontrer sur la même ligne, mais ne pas se croiser.
Nous pouvons transformer le monde d'une corde en une ligne éolienne en la fermant en cercle (Fig. 6). Dans ce document, deux funambules ne pouvaient pas non plus se croiser - c'est la propriété principale des mondes unidimensionnels. Et ce serait toujours la dimension finale. Mais le funambule dans une telle situation pouvait déjà marcher en cercle en continu et sans fin, sans s'arrêter.
Fig. 6Autres mondes unidimensionnels connus (effectivement):
- La route étroite est un monde unidimensionnel pour les voitures;
- Un chemin étroit avec une falaise - pour un touriste escaladant une montagne;
- Les étages d'un immeuble de grande hauteur sont destinés à un ascenseur.
En général, le monde reste tridimensionnel, mais pour décrire une voiture, un touriste ou un ascenseur, une seule dimension doit être représentée.
À l'avenir, souvenez-vous: nous vivons dans un monde tridimensionnel apparent, et tout ce que nous rencontrons nous semble tridimensionnel. Mais parfois, notre monde tridimensionnel (plus précisément, une partie de celui-ci) peut se comporter aussi efficacement unidimensionnel ou bidimensionnel (pouvez-vous trouver des exemples?) Ou même zéro dimensionnel! (Tous ceux qui n'ont pas de chance de se retrouver coincés dans un embouteillage qui ne bouge pas savent ce qu'est ce monde à zéro dimension!) Cette intuition nous sera très utile plus tard.