La connexion secrète des mathématiques pures et de la physique est révélée

Un mathématicien exceptionnel a révélé les détails de la façon dont ses succès dans l'étude des problèmes mathématiques millénaires sont liés à des concepts empruntés à la physique.

Mignon Kim

Les mathématiques regorgent de systèmes numériques étranges dont la plupart des gens n'ont jamais entendu parler. Certains d'entre eux seront même difficiles à imaginer. Mais les nombres rationnels sont connus de tous. Ce sont des nombres pour compter les objets et les fractions - tous les nombres que nous connaissons de l'école primaire. Mais en mathématiques, les choses les plus simples sont parfois les plus difficiles à comprendre. Ils sont simples, comme un mur lisse, sans fissures et protubérances, ou d'autres propriétés évidentes que vous pourriez saisir.

Minion Kim , mathématicien à l'Université d'Oxford, s'intéresse particulièrement à la question de savoir quels nombres rationnels conviennent pour résoudre des équations d'un certain type. Ce problème a stimulé les spécialistes de la théorie des nombres depuis des millénaires. Et ils ont à peine progressé vers sa solution. Lorsqu'une question a été étudiée pendant si longtemps et sans réponse, on peut conclure que la seule façon de progresser est de proposer une idée radicalement nouvelle. C'est exactement ce que Kim a fait.

«Il n'y a pas beaucoup de technologie qui existe, même si nous y travaillons depuis 3000 ans. Donc, quand quelqu'un propose une façon vraiment nouvelle de le faire, c'est d'un grand intérêt - et Mignon a fait exactement cela », a déclaré Jordan Ellenberg, mathématicien à l'Université du Wisconsin à Madison.

Au cours de la dernière décennie, Kim a décrit une toute nouvelle façon de trouver des modèles dans le monde apparemment désordonné des nombres rationnels. Il a décrit cette méthode dans des articles et lors de conférences, et l'a transmise aux étudiants qui poursuivent maintenant ce travail seuls. Mais il a toujours sauvé quelque chose. Sa vision, qui a donné vie à ses idées, ne reposait pas sur un monde pur de nombres, mais sur des concepts empruntés à la physique. Pour Kim, les décisions rationnelles rappellent quelque peu la trajectoire de la lumière.


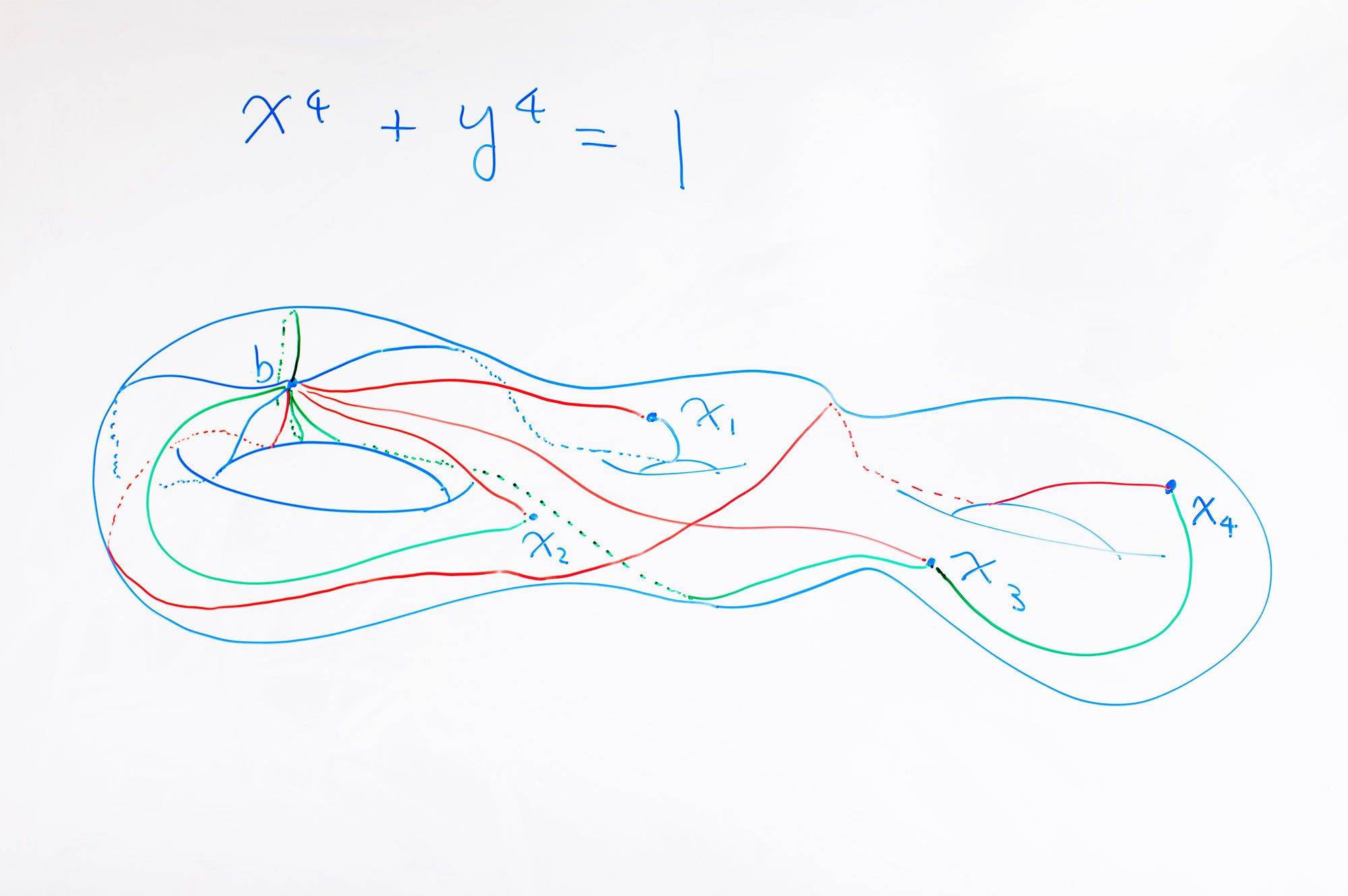Un objet mathématique, un tore à trois trous, orne le tableau de Kim à l'Université d'Oxford.

Si cette connexion semble fantastique, elle l'est, même pour les mathématiciens. Par conséquent, Kim n'a pas divulgué ses détails depuis longtemps. «Je l'ai caché parce que pendant de nombreuses années, j'ai été troublé par le lien avec la physique», dit-il. "Les spécialistes de la théorie des nombres sont des gens très pratiques, et l'influence de la physique les rend parfois sceptiques vis-à-vis des mathématiques."

Mais maintenant, Kim dit qu'il est prêt à partager sa vision. "Je pense que le changement n'est qu'un symptôme du vieillissement!" - a écrit Kim, qui a eu 53 ans, dans l'une des premières lettres que nous avons échangées pour écrire cette histoire.

Il a récemment tenu une conférence qui a réuni des experts en théorie des nombres et en théorie des cordes. Il a également esquissé des ébauches d'articles commençant à décrire son inspiration pour la communauté mathématique, peu habituée à penser aux nombres en utilisant de telles analogies directes avec le monde physique.

Un seul obstacle subsiste - la dernière partie de l'analogie de la physique en mathématiques, que Kim n'a pas encore mise au point. Il espère qu'en invitant d'autres personnes à partager sa vision, en particulier des physiciens, il recevra l'aide nécessaire pour achever les travaux.

Devinette ancienne

Les solutions rationnelles d'équations attirent activement l'esprit humain. Ils apportent une satisfaction, similaire à ce que vous obtenez des pièces du puzzle qui se mettent en place. Ils sont donc les héros des hypothèses mathématiques les plus connues.

Les nombres rationnels comprennent des nombres entiers et tout nombre qui peut être exprimé comme le rapport de deux nombres entiers, par exemple 1, -4 ou 99/100. Les mathématiciens sont particulièrement intéressés par les nombres rationnels qui résolvent les équations diophantiennes - équations polynomiales avec des coefficients entiers, par exemple, x ² + y ² = 1. Ils sont nommés d'après le mathématicien Diophantus , qui les a étudiés à Alexandrie au 3ème siècle après JC.

Les solutions rationnelles sont difficiles à trouver dans le cas général, car elles n'obéissent à aucune régularité géométrique. Prenez l'équation x ² + y ² = 1. Ses solutions en nombres réels forment un cercle. Supprimez tous les points du cercle qui ne peuvent pas être exprimés en fractions, et seules les décisions rationnelles resteront qui ne forment pas un tel objet soigné. Les solutions rationnelles semblent dispersées au hasard sur la circonférence.



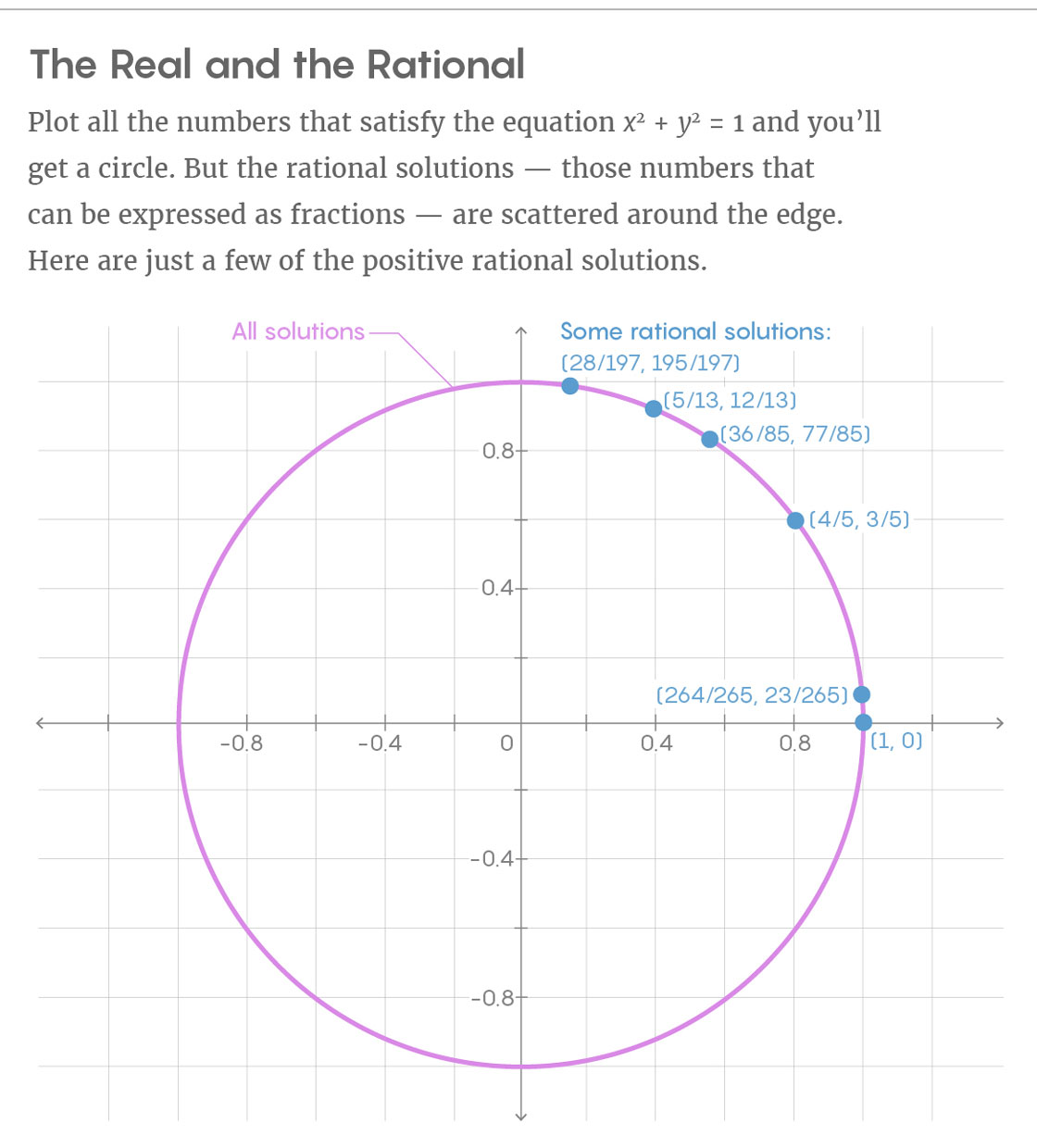
«La condition à laquelle le point doit obéir pour avoir des coordonnées rationnelles n'est pas du tout géométrique. Il est impossible d'écrire une équation que les points rationnels doivent satisfaire », explique Kim.

Il est souvent assez simple de trouver une solution rationnelle, voire plusieurs. Mais les mathématiciens qui n'aiment pas l'euphémisme sont plus intéressés à trouver toutes les solutions rationnelles. Et c'est beaucoup plus compliqué. C'est si difficile que, la preuve d'une déclaration, même mineure, sur le nombre de décisions rationnelles est suffisante pour passer pour un luminaire mathématique. En 1986, Gerd Falting a remporté le Fields Prize , la plus haute récompense mathématique, principalement pour avoir prouvé l'hypothèse de Mordell , selon laquelle certaines classes d'équations diophantiennes n'ont qu'un nombre fini de solutions rationnelles.

La preuve de Falting a marqué un tournant dans la théorie des nombres. Et aussi par ce que les mathématiciens appellent «preuve inefficace», car elle ne donne pas le nombre exact de solutions rationnelles et ne les trouve pas. Depuis lors, les mathématiciens ont cherché des moyens de faire ces prochaines étapes. Les points rationnels semblent aléatoires sur un graphique d'équation régulier. Les mathématiciens espèrent qu'en changeant le contexte dans lequel ils réfléchissent à un problème, ces points peuvent ressembler à une combinaison significative qui peut être décrite d'une manière exacte. Le problème est que les domaines bien connus des mathématiques ne fournissent pas un tel contexte.


Kim dans son bureau à Oxford

"Afin d'obtenir des résultats efficaces à partir de points rationnels, il est clairement nécessaire d'avoir une nouvelle idée", a déclaré Ellenberg.

Il y a maintenant deux hypothèses principales sur la nature d'une telle idée. L'une vient du mathématicien japonais Shinichi Motizuki , qui a publié en 2012 un ouvrage mathématique complexe et innovant de plusieurs centaines de pages sur la page de sa faculté de l'Université de Kyoto. Cinq ans plus tard, ce travail reste largement incompréhensible. Une autre nouvelle idée est venue de Kim, qui a essayé d'imaginer des nombres rationnels dans un contexte numérique étendu dans lequel leurs modèles cachés commencent à apparaître.

Solution symétrique

Les mathématiciens disent souvent que plus un objet est symétrique, plus il est facile de l'étudier. Par conséquent, ils aimeraient placer l'étude des équations diophantiennes dans des conditions contenant plus de symétrie que celles où ce problème se pose naturellement. Si cela réussit, ils pourront utiliser les nouvelles symétries pour suivre les points rationnels dont ils ont besoin.

Pour comprendre comment la symétrie aide un mathématicien à naviguer dans un problème, imaginez un cercle. Votre objectif est peut-être d'identifier tous les points du cercle. La symétrie aide beaucoup, car elle crée une carte qui vous permet de passer des points que vous connaissez à ceux qui restent à découvrir.

Imaginez que vous avez trouvé tous les points rationnels au bas d'un cercle. Comme le cercle a une symétrie miroir, les points peuvent être réfléchis vers le haut (en changeant les signes à toutes les coordonnées y) et obtenir soudainement tous les points du haut. Le cercle en général a une symétrie si riche que pour rechercher tous les points sur celui-ci, vous devez trouver la position d'un seul point, puis le combiner avec des connaissances sur la symétrie du cercle: il vous suffit d'appliquer la symétrie de rotation infinie du cercle au point de départ.

Mais si l'objet géométrique avec lequel vous travaillez est beaucoup moins correct, comme, par exemple, un chemin ondulant de manière aléatoire, vous devrez beaucoup travailler pour déterminer chaque point séparément - vous n'aurez pas de relations symétriques qui vous permettront de marquer des points inconnus lorsque aider célèbre.

Les ensembles numériques peuvent également avoir des symétries, et plus il y a de symétries dans un ensemble, plus il est facile à comprendre - vous pouvez appliquer des relations symétriques pour détecter des valeurs inconnues. Les nombres avec certains types de symétrie forment un «groupe», et les mathématiciens utilisent les propriétés du groupe pour comprendre les nombres qu'il contient.

De nombreuses solutions rationnelles de l'équation n'ont pas à avoir de symétrie et ne forment pas un groupe, c'est pourquoi les mathématiciens sont confrontés à une tâche irréaliste lorsqu'ils essaient de trouver des solutions une par une.

À partir des années 40, les mathématiciens ont commencé à étudier les méthodes pour organiser les équations diophantiennes dans des conditions plus symétriques. Le mathématicien Claude Chabauty a découvert qu'à l'intérieur de l'espace géométrique plus grand qu'il a créé (en utilisant un univers étendu de nombres appelés nombres p-adiques ), les nombres rationnels forment leur propre sous-espace symétrique. Il a pris ce sous-espace et l'a combiné avec un tracé de l'équation diophantienne. Les points de leur intersection se sont avérés être des solutions rationnelles de l'équation.

Dans les années 1980, le mathématicien Robert Coleman a précisé le travail de Chaboti. Au cours des deux décennies suivantes, l'approche de Coleman-Chaboti a été le meilleur outil mathématique dont les mathématiciens disposaient pour trouver des solutions rationnelles aux équations diophantiennes. Mais cela ne fonctionne que si le graphique de l'équation est en corrélation avec la taille d'un plus grand espace dans une certaine proportion. Lorsqu'il est rompu, il devient difficile de trouver avec précision la position des points d'intersection de la courbe d'équation et des nombres rationnels.

"Si votre courbe se trouve dans un environnement où il y a trop de points rationnels, ils commencent à s'accumuler et il vous est difficile de distinguer ceux qui se trouvent sur la courbe", a déclaré Kiran Kedlaya, mathématicien à l'Université de Californie à San Diego.

Et puis Kim entre. Pour élargir le travail de Chaboti, il voulait trouver un espace encore plus grand dans lequel étudier les équations diophantiennes - un espace où les nombres rationnels sont plus fragmentés, ce qui nous permet d'étudier les points d'intersection avec un grand nombre de variétés d'équations diophantiennes.

Espaces d'espaces

Si vous avez besoin d'un espace plus grand et de quelques conseils sur la façon d'utiliser la symétrie pour vous y orienter, la physique vous conviendra.

Dans le cas général, l'espace au sens mathématique est tout ensemble de points ayant une structure géométrique ou topologique. Mille points dispersés par la volonté ou non, ne forment pas d'espace - ils ne sont pas reliés entre eux par une structure. Mais la sphère, qui est une organisation connectée de points, est déjà l'espace. Comme un tore, ou un plan à deux dimensions, ou un espace-temps à quatre dimensions, où nous vivons.

À cela s'ajoutent des espaces encore plus exotiques que l'on peut imaginer comme des «espaces d'espaces». L'exemple le plus simple: disons que vous avez un triangle - et c'est l'espace. Imaginez maintenant l'espace de tous les triangles possibles. Chaque point en lui représente un certain triangle, et les coordonnées de ce point sont déterminées par les angles du triangle représenté par lui.

Une telle idée est souvent utile en physique. Dans le cadre de la théorie générale de la relativité, l'espace et le temps évoluent constamment et les physiciens considèrent chaque configuration de l'espace et du temps comme un point dans l'espace de toutes les configurations espace-temps. Des espaces d'espaces apparaissent également dans la zone que les physiciens appellent l'invariance de jauge, travaillant avec des champs superposés à l'espace physique. Ces champs décrivent comment des forces comme l'électromagnétisme et la gravité changent lorsqu'elles se déplacent dans l'espace. On peut imaginer qu'à chaque point de l'espace la configuration de ces champs est légèrement différente - et que toutes ces configurations différentes forment des points dans «l'espace de tous les champs» de dimension supérieure.

Cet espace de champs de la physique est une analogie proche de la proposition de Kim pour la théorie des nombres. Pour comprendre cela, imaginez un rayon de lumière. Les physiciens représentent la lumière se déplaçant dans l'espace des champs de dimension supérieure. Dans cet espace, la lumière suivra un chemin qui adhère au principe de moindre résistance et minimise le temps nécessaire pour aller d'un point A à un point B. Ce principe explique pourquoi la lumière se plie lors du passage d'un matériau à un autre - un chemin incurvé minimise le temps les coûts.

Les plus grands espaces d'espaces apparaissant en physique ont des symétries supplémentaires qui ne sont présentes dans aucun des espaces qu'ils représentent. Ces symétries attirent l'attention sur certains points, par exemple en se concentrant sur un chemin qui minimise le temps. Les mêmes symétries, construites différemment et dans un contexte différent, peuvent être accentuées à d'autres points - par exemple, à des points correspondant à des solutions rationnelles d'équations.

Connecter la symétrie à la physique

Dans la théorie des nombres, il n'y a pas de particules qui pourraient être suivies, mais elle a quelque chose comme l'espace-temps, et elle offre un moyen de dessiner des chemins et de créer l'espace de tous les chemins possibles. À partir de cette correspondance de base, Kim développe des schémas dans lesquels «le problème de trouver la trajectoire de la lumière et de trouver des solutions rationnelles des équations diophantiennes sont les deux faces du même problème», comme il l'a expliqué lors d'une conférence sur la physique mathématique à Heidelberg la semaine dernière.

Les solutions d'équations diophantiennes forment des espaces - ce sont des courbes définies par des équations. Ces courbes peuvent être unidimensionnelles, comme un cercle, ou multidimensionnelles. Par exemple, si vous construisez une solution complexe de l'équation diophantienne x ⁴ + y ⁴ = 1, vous obtenez un tore à trois trous. Les points rationnels sur un tel tore n'ont pas de structure géométrique - c'est pourquoi il est difficile de les trouver - mais ils peuvent être comparés à des points dans un espace multidimensionnel d'espaces possédant une telle structure.



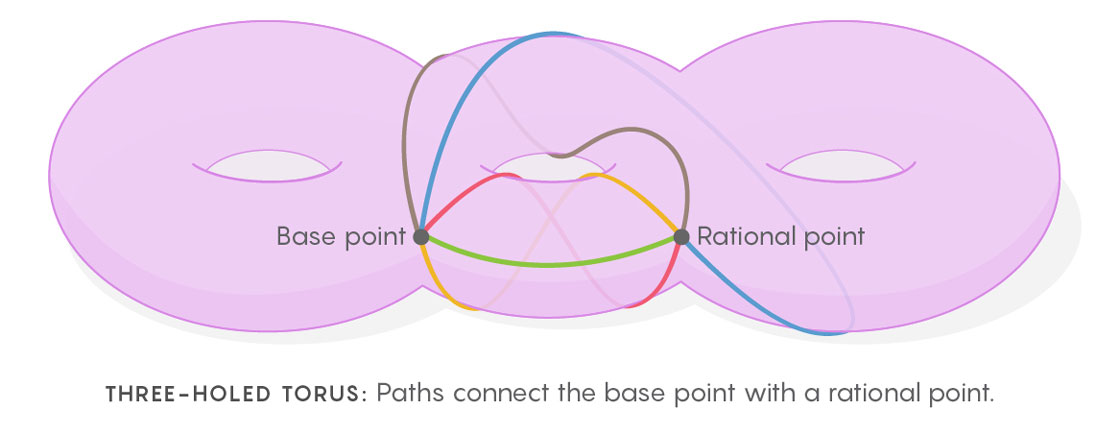
Kim crée cet espace multidimensionnel d'espaces, imaginant les façons dont les courbes fermées peuvent être dessinées sur le tore (ou dans l'espace qui définit l'équation). La procédure pour dessiner des courbes ressemble à ceci. Vous devez d'abord sélectionner le point de départ, puis dessiner une boucle de ce point à n'importe quel autre et revenir au premier. Répétez maintenant ce processus en traçant les chemins reliant le point de base à tous les autres points du tore. Vous obtiendrez le fourré de toutes les boucles possibles commençant et se terminant au point de base. Cet ensemble de boucles est un objet mathématique d'importance centrale appelé le groupe fondamental de l' espace.

Tout point du tore peut être utilisé comme point de départ. Chaque point aura un fourré unique de chemins qui en émane. Chacune de ces collections de chemins peut être représentée comme un point dans un «espace multidimensionnel de tous les ensembles de chemins» (comme l'espace de tous les triangles possibles). Cet espace d'espaces est géométriquement très similaire à ce que les physiciens construisent dans la théorie de l'invariance de jauge: la façon dont les ensembles de chemins changent lorsque vous passez d'un point sur un tore à un autre est très similaire à la façon dont les champs changent lorsque vous passez d'un point à un autre dans l'espace réel. Cet espace d'espaces a des symétries supplémentaires qui ne sont pas sur le tore lui-même. Et bien que les points rationnels sur un tore n'aient pas de symétrie, si nous allons dans l'espace de tous les ensembles de chemins, nous pouvons trouver des symétries entre les points associés aux nombres rationnels. Vous obtenez des symétries qui n'étaient pas visibles auparavant.

"Je dis parfois que" la symétrie arithmétique latente "est codée dans ces chemins, ce qui est très similaire aux symétries internes de la théorie de l'invariance de jauge", a déclaré Kim.

Comme Chaboti, Kim trouve des solutions rationnelles en explorant les points d'intersection dans le plus grand espace qu'ils ont créé. Il utilise les symétries de cet espace pour arriver aux points d'intersection. Il espère développer une équation qui définit précisément ces points.

Dans le contexte physique, on peut imaginer toutes les voies possibles d'un rayon de lumière. Ceci est votre "espace de tous les chemins". Les physiciens s'intéressent aux points de cet espace correspondant à des chemins qui minimisent le temps. Kim pense que les points correspondant aux fourrés de chemins émanant de points rationnels ont quelque chose en commun avec la même propriété - c'est-à-dire que ces points minimisent certaines propriétés qui se produisent lorsque l'on considère les formes géométriques des équations diophantiennes. Il n'a tout simplement pas encore compris ce que pourrait être cette propriété.

«Ce que j'ai commencé à chercher», c'est le principe de moindre résistance dans un contexte mathématique, m'écrit-il dans une lettre. "Je ne l'ai pas encore trouvé, mais je suis sûr qu'il existe."

Un avenir incertain

Au cours des derniers mois, j'ai décrit la vision de Kim, inspirée par la physique, par plusieurs mathématiciens, fans de ses contributions à la théorie des nombres. Mais en apprenant un tel détail de son travail, ils ont été perdus.

"En tant que théoricien des valeurs représentatives, si on me montrait toutes ces réalisations incroyables faites par le Minion et qu'on me demandait si elles étaient inspirées par la physique, je dirais: De quoi diable parles-tu?" - dit Ellenberg.

Jusqu'à présent, Kim n'a mentionné la physique dans aucun de ses travaux. Au lieu de cela, il écrit sur des objets appelés «variations Selmer» et examine la relation entre les variations Selmer dans l'espace de toutes les variations Selmer. Ces choses sont familières aux experts en théorie des nombres. Mais pour Kim, ils n'étaient toujours qu'une autre désignation de certains objets physiques.

"Il devrait y avoir un moyen d'utiliser des idées physiques pour résoudre des problèmes dans la théorie des nombres, mais nous n'avons pas encore suffisamment réfléchi à la façon de créer une telle plate-forme", a déclaré Kim. «Nous sommes dans un état où notre compréhension de la physique est assez bien développée, et de nombreux spécialistes de la théorie des nombres s'y intéressent afin de passer à l'étape suivante.»

Le principal obstacle à la méthode Kim est de trouver une action pour minimiser l'espace de tous les ensembles de boucles. Dans le monde physique, cette approche semble naturelle, mais en arithmétique, elle n'a pas de signification évidente. Même les mathématiciens qui surveillent de près le travail de Kim ne sont pas sûrs de pouvoir le retrouver.

«Je pense que le programme de Kim fera beaucoup de choses merveilleuses pour nous. "Je ne pense pas que nous aurons aussi clair que Mignon veut comprendre si les points rationnels sont des solutions classiques à la théorie de la jauge arithmétique", a déclaré Arnav Tripathy, professeur de physique mathématique à l'Université Harvard.

Aujourd'hui, le langage de la physique ne recoupe presque pas la pratique de la théorie des nombres. Kim pense que cela va certainement changer. Il y a quarante ans, la physique, la géométrie et la topologie avaient peu de choses en commun. Puis, dans les années 80, plusieurs mathématiciens et physiciens, devenus des figures importantes, ont trouvé des moyens exacts d'utiliser la physique pour étudier les propriétés des formes. Après ce développement, cette zone a changé et n'est pas revenue aux méthodes précédentes.

«De nos jours, il est pratiquement impossible de s'intéresser à la géométrie et à la topologie sans rien savoir de la physique. Je suis presque sûr que cela se produira également avec la théorie des nombres »au cours des 15 prochaines années, a déclaré Kim. "Toutes les connexions sont extrêmement naturelles."