Dimensions supplémentaires: mondes bidimensionnels

À partir d'un article sur les mondes unidimensionnels, vous savez que le monde fait unidimensionnel parce que la position qu'il contient est déterminée par une unité d'information.

Il doit également être continu (ou proche de continu d'un point de vue pratique). J'ai décrit plusieurs exemples de dimensions: une ligne de revenus, infinie, et représentée par une ligne infinie; ligne arc-en-ciel, finale, avec murs d'enceinte, représentée par un segment; Ligne de direction du vent éolien, périodique-finie, représentée par un segment dans lequel l'extrémité gauche coïncide avec la droite, ou, ce qui est le même, un cercle. En passant, j'ai mentionné un autre exemple - un monde sans fin dans un sens et fini dans un autre. Dans un autre article, j'ai souligné qu'il existe de nombreux types de mesures, mais les dimensions physiques de l'espace ont des propriétés uniques et spéciales (ainsi que très évidentes) qui les distinguent des mesures d'un autre type.


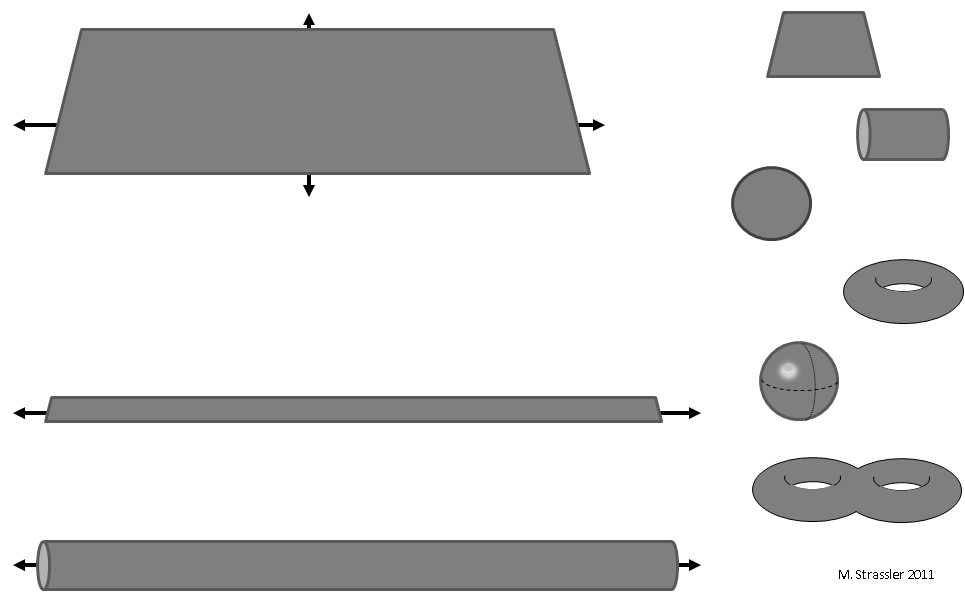Fig. 1: mondes à deux dimensions

Et les mondes à deux dimensions? Il n'est pas surprenant qu'il existe beaucoup plus de types de mondes bidimensionnels que de types de mondes unidimensionnels. Quelques exemples de tels espaces sont illustrés à la Fig. 1. Vous pouvez imaginer un monde sans fin dans les deux sens: un avion (en haut à gauche). On peut imaginer un monde sans fin dans un sens et dans un autre qui forme soit un segment soit un cercle. Ces mondes sont naturellement appelés une bande et un tuyau (en bas à gauche). On peut imaginer le monde final dans les deux sens (la partie droite de la Fig. 1). Et combien d'opportunités sont là! Seulement sur cette figure, vous pouvez voir de haut en bas un carré, un cylindre (la partie ronde de la boîte sans couvercle ni intérieur), un disque, un tore (quelque chose comme un pneu de voiture), une sphère (uniquement la surface), un pneu double. Et ce ne sont pas toutes des options. S'ils sont extrapolés à l'avenir, il devient clair que lorsque nous arriverons aux trois dimensions et continuerons, nous ne serons plus en mesure de compiler de telles listes.

Comme pour les espaces unidimensionnels, la position dans l'espace bidimensionnel est déterminée par deux unités d'information.

Un exemple de sphère (avec une bonne approximation) peut être la surface de la Terre: tout emplacement peut être indiqué par la latitude et la longitude. Une fourmi, marchant le long d'un tuyau d'arrosage, se déplace le long d'un tuyau bidimensionnel et se trouve à tout moment à une certaine distance de la grue et à un certain angle par rapport à la verticale. Une autoroute à plusieurs voies est essentiellement une bande à deux dimensions avec un côté très long et un côté court: les deux unités d'informations nécessaires pour déterminer votre position sont la distance depuis le début de la route et la distance depuis son bord droit.

Rappelez-vous la ligne de revenus. «Votre revenu pour l'année écoulée est un certain nombre dans votre devise locale. Elle peut être positive ou négative, grande ou petite; il peut être représenté comme un point sur une ligne, comme dans la fig. 1, que nous appellerons le «point de revenu». Chaque point de la ligne représente un retour possible. » Si vous êtes marié et que votre conjoint et vous avez un revenu, les deux flux de trésorerie entrant dans votre ménage peuvent être représentés comme un plan à deux revenus. Deux chiffres décrivant un point sur cet avion seront vos revenus et les revenus de votre conjoint.

Et voici un exemple astucieux d'un tore montrant comment on peut imaginer des formes bidimensionnelles intéressantes dont les dimensions ne sont pas des dimensions de l'espace physique. Dans la fig. 3 articles sur les mondes unidimensionnels, nous avons vu que les directions possibles du vent forment un monde unidimensionnel sous la forme d'un cercle (ou d'une ligne où le début et la fin coïncident). Les directions de navigation possibles forment également un cercle similaire. Mais tous ceux qui ont navigué savent qu'il n'est pas nécessaire de se déplacer dans la même direction que le vent souffle; si vous placez la voile à un angle, vous pouvez vous déplacer vers l'ouest, même si le vent souffle du nord. Donc, si je demande deux informations - de quelle direction le vent souffle et dans quelle direction mon voilier se déplace - les deux seront des points sur le cercle. Deux informations, situées sur un cercle, indiquent un point sur le tore.

Avant de continuer, je mentionnerai une confusion naturelle et répandue. Je l'ai déjà fait allusion dans la description des différents mondes donnée ci-dessus. Ne confondez pas les mesures des formes elles-mêmes avec une certaine manière de représenter ces dimensions ou formes! La propriété du cercle est telle que si vous vous déplacez dans n'importe quelle direction, vous reviendrez à l'endroit où vous avez commencé. Le cercle n'a rien à l'intérieur ni à l'extérieur. Le simple fait de représenter un cercle sous la forme d'une courbe fermée sur un plan bidimensionnel semble avoir une partie intérieure et extérieure. Mais c'est simplement une propriété de représenter le cercle sur le plan, et non une propriété du cercle lui-même.