Partenariat Partenaires Kaluza-Klein, partie 2

Dans un article précédent, j'ai expliqué pourquoi il semblerait aux observateurs naïfs qui ne sont pas conscients de la présence d'une dimension supplémentaire qu'une particule capable de se déplacer dans des dimensions supplémentaires a des partenaires de Kaluza-Klein (KK) - des versions plus lourdes de la particule d'origine. J'ai souligné que lorsque la particule initiale de masse m se déplace dans la direction de la dimension supplémentaire, elle semble à l'observateur naïf immobile et plus lourde qu'elle ne devrait l'être, c'est-à-dire comme s'il s'agissait d'une particule d'un type différent. Cette classe de particules soi-disant nouvelles, similaires à l'original, mais plus lourdes, est appelée partenaires QC.

Dans le cas d'une bande , si une particule de masse m se déplace à travers la bande avec un moment p en _travers , l'observateur qui considère la bande comme une ligne supposera que la particule est un partenaire KK avec une impulsion et une masse M nulles, où

$$

$$M ^ 2 = m ^ 2 + (p_ {across} / c) ^ 2> m ^ 2$$

Bien que cela soit généralement vrai, il s'ensuit que pour chaque masse M supérieure à m, il doit y avoir son propre partenaire QC. Mais ce n'est pas le cas - notre monde est quantique (voir la figure 1 de l'article précédent). Maintenant, nous découvrons exactement comment la mécanique quantique change la situation dans son ensemble.

La caractéristique clé de la physique quantique dont nous avons besoin est que pour une «particule» quantique se déplaçant dans une mesure de taille finie, toutes les valeurs possibles de p à _{travers ne sont pas} autorisées. Dans une formulation plus générale: la mécanique quantique suggère qu'une «particule» se déplaçant dans une mesure de taille finie ne peut avoir que certaines valeurs de quantité de mouvement dans cette direction.

C'est l'une des conséquences les plus importantes et les plus étranges de la mécanique quantique! À première vue, cela est complètement contre-intuitif, car qu'est-ce qui peut vous empêcher de demander à la «particule» avec l'élan p une légère accélération de sorte que son élan soit légèrement différent de p?

Qu'est-ce qu'un quantum?

Vous avez peut-être remarqué que j'ai commencé à citer le mot «particule», car dans le contexte actuel, nous devons distinguer le terme «particule», utilisé pour décrire les électrons, les muons, les quarks, les gluons et toutes les autres particules élémentaires connues, d'un concept intuitif particules que nous héritons de notre expérience avec la poussière, le sable, le sel et le gravier. Il serait préférable d'appeler de telles "particules" comme un électron, un photon, un Quark, etc., des quanta, des objets plus rusés. Ces quanta sont des perturbations des champs, ils ressemblent beaucoup plus à des ondes qu'à des particules. La meilleure façon de comprendre le quantum est d'imaginer des vagues. Ceci est un autre point linguistique important: quand je dis «vague», je ne veux pas dire quelque chose comme une vague séparée dans l'océan se brisant sur le rivage - je veux dire une séquence de vagues avec de nombreuses crêtes et creux.

Un exemple de telles ondes sera les ondes électromagnétiques, qui comprennent également des ondes lumineuses, visibles à nos yeux. Imaginez que nous prenions une telle onde - par exemple, la lumière laser - et que nous diminuions de plus en plus la lumière. Comment peut-il être étouffé? Il s'avère que dans notre monde quantique, il y a le plus léger éclair de lumière possible que nous appelons un quantum de lumière, ou un photon. Un photon est une onde de lumière dont la hauteur et l'intensité des ondes sont les plus petites possibles. Nous devons tous ces concepts et noms à Einstein qui, malgré son mécontentement bien connu des conséquences conceptuelles de la mécanique quantique, a été l'un des fondateurs de cette théorie.

Il n'y a rien d'intuitif - de mon point de vue - que les ondes lumineuses soient composées de quanta, car cela ne se manifeste dans aucun des processus que nous observons directement. Mais notre corps, grâce à des processus que nous ne connaissons pas, utilise constamment ce fait. La lumière de la lampe semble continue à notre cerveau, mais nos yeux absorbent réellement les photons un à la fois. De plus, j'ai vu de mes propres yeux la confirmation que la lumière est constituée de quanta - je le sais non seulement dans les livres.

Nous, physiciens, appelons souvent ces quanta de lumière «particules de lumière», car à bien des égards, ils se comportent comme des particules. Tout photon se déplaçant en ligne droite par lui-même, a une certaine énergie et un certain élan; tous les photons ont la même valeur de masse (spécifiquement, zéro); un photon ne peut pas être divisé en parties plus petites; un photon ne peut être émis ou absorbé que dans son intégralité. Ces propriétés correspondent à peu près à ce que notre intuition pourrait attendre de particules telles que des grains de sable, des billes de verre, des particules de poussière, etc.

Mais le mot "quantique" pour de nombreuses raisons est meilleur que le mot "particule", car certaines propriétés des quanta sont similaires aux propriétés des particules, et certaines aux propriétés des ondes. Un exemple bien connu du comportement des vagues est un moyen quantique de passer par deux portes en même temps et d'interagir (dans le même sens que les vagues interagissent entre elles et que les crêtes avec des auges se détruisent mutuellement) avec elles-mêmes. Et puis nous verrons un autre exemple.

Il faut se rappeler que ce qui est fait pour le photon l'est aussi pour toutes les "particules" connues. En effet, chacun d'eux est un type de quantum - les ondes de la hauteur la plus basse possible dans le champ correspondant. Un électron est un quantum d'un champ électronique. Quark est un quantum d'un champ de quark. La particule Z est le quantum du champ Z, etc.

Quantums - QC partners

Il est temps de découvrir ce que je vous avais promis de vous expliquer: pourquoi la nature ondulatoire des quanta implique que les masses de particules des partenaires KK prennent des valeurs définies, et pas toutes les valeurs possibles, de grandes masses m de la "particule" d'origine. Le célèbre physicien Louis de Broglie , suivant les traces des premières idées d'Einstein, a clairement défini pour la première fois que la relation entre les ondes, les particules et les quanta implique que pour un quantum il existe une relation entre:
• Son impulsion (une propriété ressemblant aux propriétés des particules),
• Et sa longueur d'onde (une propriété ressemblant aux propriétés des vagues) [et encore, ici par «onde», nous entendons une séquence d'ondes, et la longueur d'onde se réfère à la distance entre les crêtes des vagues dans la séquence].

Et cette dépendance s'exprime simplement: moment = h / longueur d'onde

h est la célèbre constante de Planck , la même constante fondamentale de la nature que la vitesse de la lumière. Planck a introduit cette constante en 1900, essayant de percer un phénomène physique mystérieux. Ce fut le premier pas vers la nature quantique du monde. Chaque fois que vous essayez de décrire un phénomène dans lequel la mécanique quantique joue un rôle important, la constante h apparaît. Dans de nombreuses formules, vous pouvez voir la valeur ℏ, et ce n'est que h divisé par 2π, car cette valeur est souvent plus pratique pour simplifier les formules.


Fig. 1: considérons un quantum se déplaçant le long d'une bande et le long d'un tuyau

Dans certains cas, il s'avère un peu plus facile d'expliquer ce qui arrive au quantum se déplaçant le long du tuyau qu'à ce qui se déplace le long de la bande que nous avons utilisé dans les exemples précédents. Presque tout ce qui fonctionne pour le tuyau sera vrai pour la bande. Par conséquent, je les utiliserai ensemble.

Le partenaire QC le plus léger

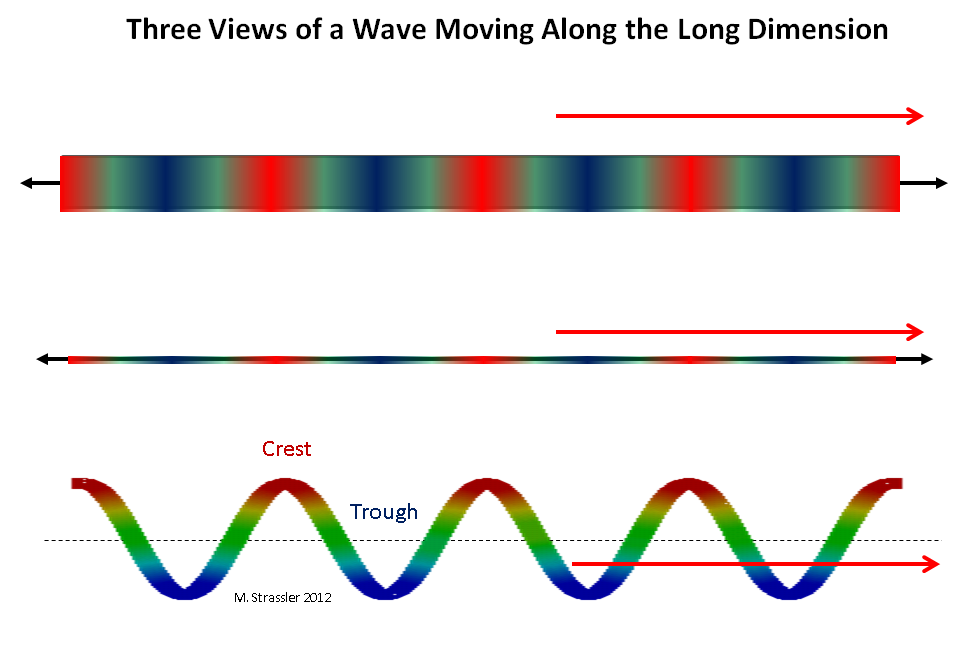Fig. 2: trois vues d'une vague se déplaçant sur une longue dimension

Imaginez un quantum voyageant le long d'une bande de largeur W, ou le long d'un tuyau de cercle S.Imaginez d'abord un quantum se déplaçant le long d'une dimension longue (long signifie infini, ou si long qu'il peut être infini, pour autant que nous puissions en juger). Une onde passant le long d'une bande ou d'un tuyau peut se déplacer le long d'une dimension longue dans n'importe quelle direction et avoir n'importe quelle longueur d'onde (la distance entre deux arêtes adjacentes). Voir fig. 2. Un tel quantum peut avoir n'importe quel élan le long d'une bande ou d'un tuyau, selon de Broglie: l'élan peut être nul, très petit, petit, grand, dans n'importe quelle direction, etc. En principe, une impulsion peut être rendue un peu plus (ou un peu moins) en poussant un quantum dans le sens de son mouvement (ou à l'inverse).


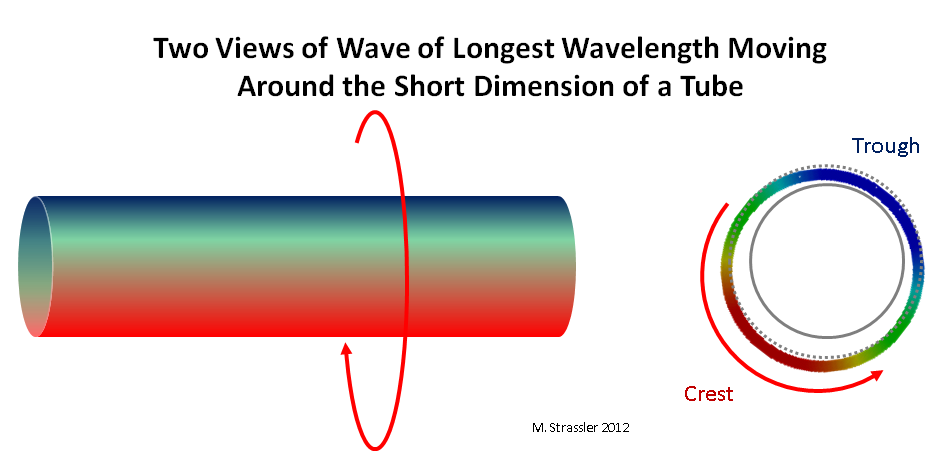Fig. 3: deux vues d'une onde se déplaçant le long d'une petite dimension d'un tuyau

Considérons maintenant un quantum (c'est-à-dire une «particule») se déplaçant à travers une bande ou un tuyau. Premièrement, il ne pourra évidemment pas avoir une longueur d'onde supérieure à la distance transversale de la bande ou à la circonférence du tuyau! Ceci est facile à voir sur le tuyau: au moins une crête (rouge) et une dépression (bleue) qui s'insèrent le long du tuyau, comme indiqué sur la fig. 3. Si la longueur d'onde est supérieure à S, l'onde ne se connectera pas à elle-même, comme le montre la Fig. 4. La longueur d'onde la plus longue sera exactement S; et la seule cavité de la vague doit être située exactement sur le côté du tuyau opposé à la seule crête.


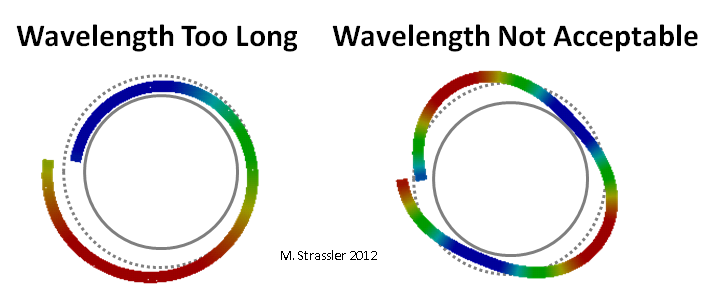Fig. 4: longueurs d'onde incorrectes

La crête et le creux de la vague de la Fig. 3 se déplacer autour du tuyau, ressemblant (Fig. 5) à une particule ordinaire non quantique (ici je veux vraiment dire quelque chose comme un grain de sable, pas un quantique ou une «particule») roulant le long du tuyau, mais avec une différence importante: si une particule intuitive ordinaire n'a pas de problèmes peut se déplacer un peu plus vite ou plus lentement, à cause de quoi son élan augmentera ou diminuera légèrement, le quantum correspondant à l'onde ne peut pas avoir un élan légèrement plus grand ou plus petit, car cela correspondrait à une longueur d'onde inacceptable (Fig.4).


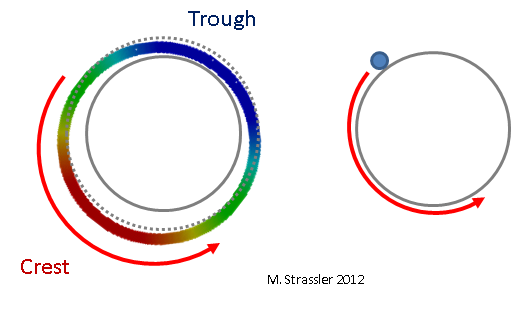Fig. 5: onde de type particules

Sur une bande, c'est un peu plus délicat, mais comme le montre la fig. 6, encore une fois, il ne peut y avoir qu'une crête sur un mur et un sur l'autre, et cette situation change avec le temps: la crête ne bouge pas, mais diminue en taille et se transforme en creux, et le creux se transforme en crête. Notez que, contrairement à la Fig. 3, où la crête et la tranchée conservent leur taille mais se déplacent le long du tuyau, la crête de cette vague ne bouge pas, mais se contracte. Par conséquent, cela s'appelle une «onde stationnaire». Pour un exemple similaire (mais pas identique), imaginez une corde de guitare ou de violon. Intuitivement, cette onde stationnaire correspond à une particule ordinaire non quantique se déplaçant vers l'avant et vers l'arrière à travers une bande. (Moins intuitivement, mais plus précisément, cela correspond à une particule ordinaire se déplaçant dans les deux directions en même temps. Mais ce fait quantique très étrange et cool n'a plus d'importance.) C'est ce que montre la Fig. 7.


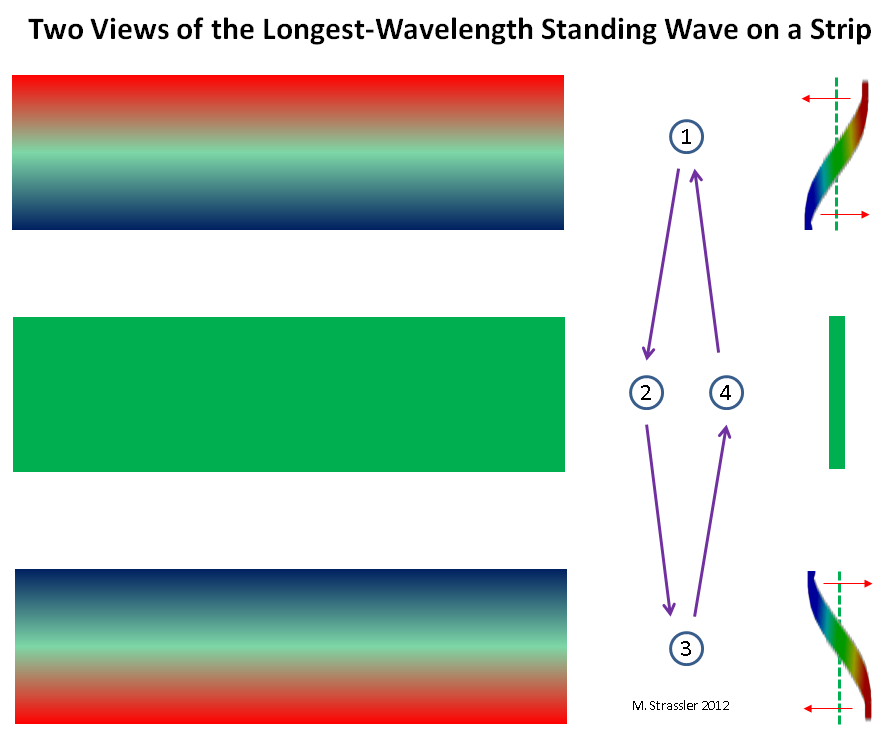Fig. 6: deux vues de l'onde stationnaire avec la plus longue longueur d'onde

Dans les deux cas, il y a la plus grande longueur d'onde possible (S pour tube, 2W pour bande). Et cela signifie qu'il y a la plus petite impulsion possible (h / S et h / 2 W pour le tube et la bande). Et enfin, cela signifie qu'il y a la particule KK la plus simple possible! Avec la masse M, où

$$

$$M ^ 2 = m ^ 2 + (p_ {à travers} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (tuyau) \\ M ^ 2 = m ^ 2 + (p_ { à travers} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (bande)$$

Notez que pour les particules sans masse, m = 0, ces formules sont réduites à:

$$

$$M = h / c S \ quad (tuyau) \\ M = h / 2 c W \ quad (bande)$$

Et ces dernières formules sont approximativement correctes si S et W sont très petits, comme c'est souvent le cas dans un raisonnement plausible.


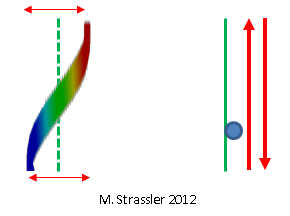Fig. 7: le quantum d'une onde stationnaire est un peu comme une particule se déplaçant d'avant en arrière

Et nous avons donc appris qu'en raison du fait que les «particules» sont en fait des quanta, avec des propriétés ressemblant aux propriétés des ondes:

• Chez le partenaire KK le plus léger, la masse M est bien supérieure à m,
• Étant donné que les formules pour M incluent 1 / W et 1 / S, plus la dimension supplémentaire est petite, plus le partenaire KK le plus léger est dur.
• En fait, lorsque S et W deviennent si petits que M dépasse largement m (ou si m est initialement nul), alors M est approximativement proportionnel à 1 / S ou 1 / W.

Super. C'est le point principal, alors assurez-vous de le comprendre avant de continuer. Une dernière chose reste à expliquer:

• Pourquoi y a-t-il de nombreux partenaires KK avec des masses différentes M, M ', M ”, etc. (où, par définition, M <M '<M ", etc.)
• Pourquoi ces masses sont-elles séparées les unes des autres?
• Pourquoi les masses grandissent-elles avec une dimension supplémentaire décroissante?
• Pourquoi les partenaires KK de différents types de particules capables de se déplacer dans la même dimension supplémentaire ont des masses similaires, en particulier pour les partenaires KK plus lourds.
• Pourquoi les masses de partenaires QC nous donneront des informations directes sur la forme, la taille et le nombre de mesures supplémentaires.

Des réponses ci-dessus peuvent être assez facilement déduites.

Au-delà du partenaire QC le plus léger

Fig. 8: onde la plus proche de la longueur d'onde la plus longue, se déplaçant le long de la courte dimension du tuyau

Pourquoi y a-t-il de nombreux partenaires KK? Tout simplement parce que les ondes quantiques sur une bande ou un tube peuvent avoir de nombreuses longueurs d'onde différentes. Dans la fig. 8, 9 et 10, on peut voir des ondes d'une longueur de 1/2 ou 1/3 du maximum, correspondant (selon Einstein et de Broglie) à un quantum d'impulsions doubles et triples par rapport au minimum.


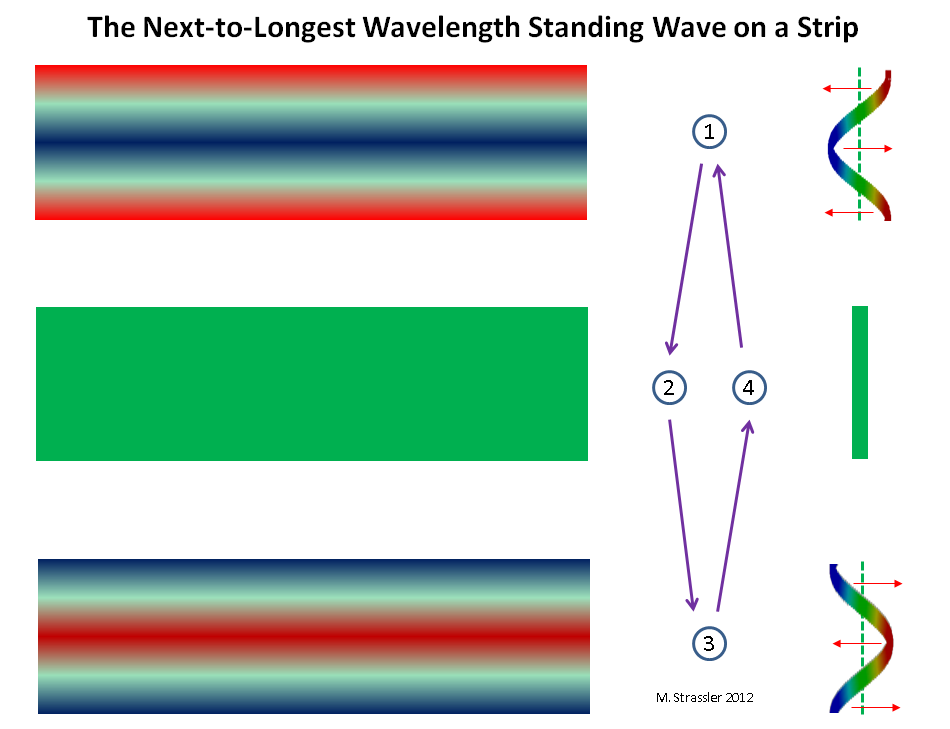Fig. 9 ondes stationnaires les plus proches de la plus longue longueur d'onde sur la bande

En résumé, nous pouvons dire que toute longueur d'onde est admissible, qui a n crêtes et n creux, où n est un entier positif (1, 2, 3, 4, ..), de sorte que la longueur d'onde est égale à S divisée par n (ou 2W divisé par n) et l'onde s'insère clairement à l'intérieur d'un cercle de cercle S ou à l'intérieur d'une ligne de longueur W. Toute autre longueur d'onde ne convient pas (voir Fig. 4). Par conséquent, compte tenu de la relation de Broglie, moment = h / longueur d'onde, toute impulsion de la forme nh / S (ou nh / 2 W) est autorisée, et pour chaque valeur de n, nous aurons un partenaire de masse KK:

$$

$$M ^ 2 = m ^ 2 + (p_ {à travers} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { à travers} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (bande)$$

Cela répond à presque toutes les questions posées, au moins pour les cas avec un tuyau et une bande:

• Il existe de nombreux partenaires QC (un pour chaque n> 0),
• Leurs masses sont bien séparées les unes des autres (puisque lorsque n change de 1, M change beaucoup),
• Leurs masses croissent avec une diminution des dimensions supplémentaires (puisque les derniers termes des formules deviennent plus grands lorsque W et S deviennent plus petits),
• Les partenaires KK lourds de particules différentes avec des masses différentes m ont des masses M similaires, car pour n suffisamment grand, les seconds termes dans les formules sont grands par rapport à m ² , ce qui donne la masse du partenaire KK approximativement égale à M = nh / c S pour le tuyau et nh / 2 c W pour la bande, et elle est presque indépendante de m.

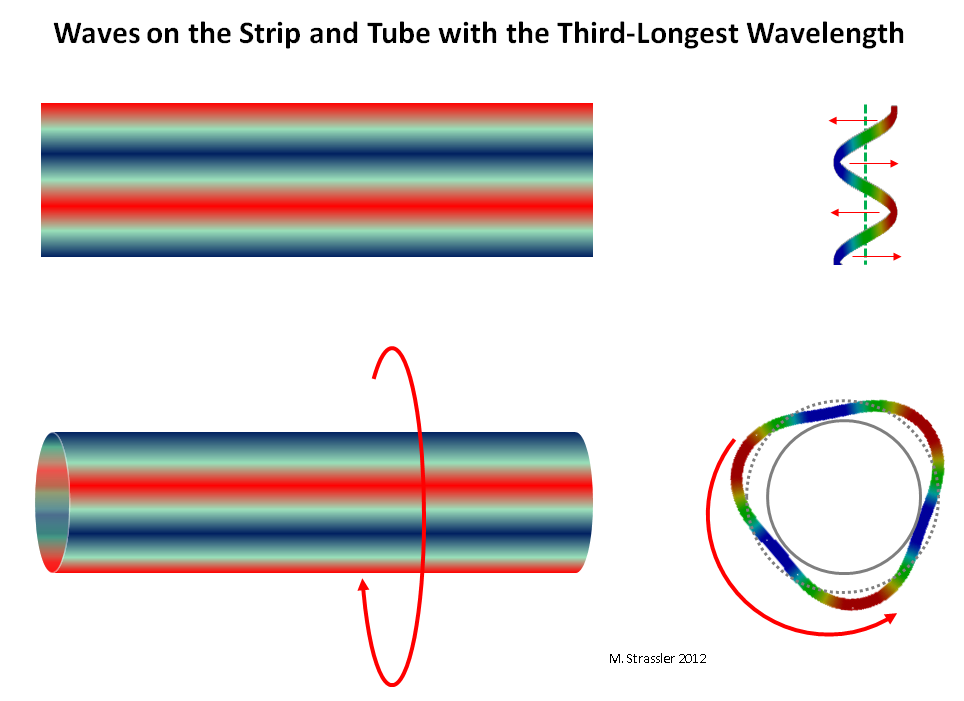Fig. 10: vagues sur une bande et un tuyau d'une longueur d'onde de 1/3 maximum

La dernière question demeure: pourquoi la quantité, la taille et la forme des dimensions supplémentaires déterminent les masses des partenaires KK - et donc, pourquoi la mesure de masse de nombreux partenaires KK vous permet de déterminer les propriétés des mesures supplémentaires, tout comme l'écoute du son d'un instrument de musique vous permet de déterminer fondamentalement sa forme , taille et matériaux dont il est fait?

Prenons un exemple extrêmement simplifié. Nous considérerons deux dimensions supplémentaires, en utilisant à nouveau notre canal de navire classique, y compris (comme nous l'avons fait à la fin d'un article récent avec des exemples de mesures supplémentaires) et le fait que le canal a de la profondeur, afin que nous puissions imaginer les vagues à l'intérieur (des vagues de ce type, vous pouvez entendre dans une grande pièce, ou sous l'eau dans n'importe quel canal). La section transversale du canal (si nous le coupons à n'importe quel point de la ligne le long de la dimension longue) ne sera qu'un rectangle de largeur W et de profondeur D.Comme toute particule non quantique, même si elle est stationnaire du point de vue de la dimension longue, elle peut se déplacer le long d'un ou de deux autres mesures (et, par conséquent, ont une impulsion en largeur ou en profondeur), et l'onde aura une longueur d'onde dans les deux dimensions supplémentaires. Une telle division simple de l'onde en ce qu'elle fait en mesurant la largeur et ce qu'elle fait en mesurant la profondeur est particulièrement liée à la rectangularité du canal, et ne fonctionnera généralement pas dans d'autres exemples. Par exemple, comme le montre la fig. 11, en haut, une des vagues autorisées aura trois creux pour mesurer la largeur et un pour mesurer la profondeur.


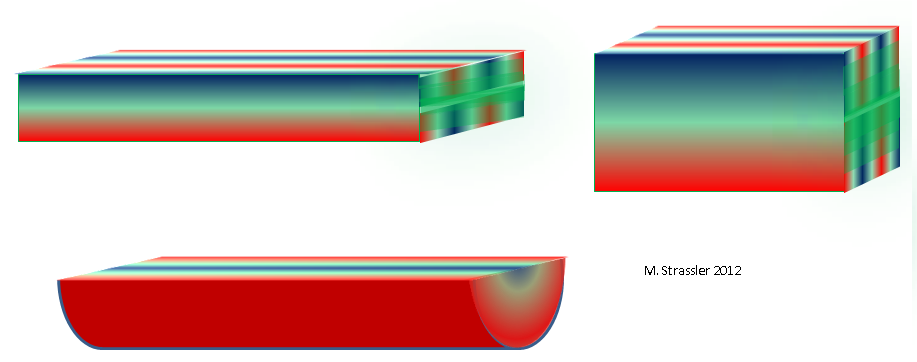Fig. 11

Nous pouvons désigner le nombre de dépressions et de crêtes en mesurant la largeur avec l'entier n ₁ , et en mesurant la profondeur - n ₂ , et pour chaque n ₁ et n ₂ (une de ces valeurs ou les deux peuvent être supérieures à zéro), nous obtenons le partenaire KK. Pour les quanta sans masse (m = 0) ou presque sans masse, les partenaires KK auront une masse

$$

$$M ^ 2 = m ^ 2 + (p_ {largeur} / c) ^ 2 + (p_ {profondeur} / c) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 c D) ^ 2$$

On peut voir que la distribution de masse est différente du cas avec une dimension supplémentaire, et qu'elle peut nous dire à la fois W et D.

Si la section transversale du canal a une forme différente, par exemple, un triangle ou un demi-disque, comme indiqué sur la Fig. 11, ci-dessous, nous obtenons une autre distribution de masse qui reflète la forme exacte d'un triangle ou d'un demi-disque. Et nous pouvons déjà éliminer les canaux pratiques des navires et représenter l'espace tridimensionnel, dont la section transversale correspond à toute autre forme bidimensionnelle finie, dont l'une est illustrée à la Fig. 1 dans un article sur les mondes à deux dimensions spatiales: un disque plein, voire une sphère ou un tore. Chacun de ces formulaires nous donnera son propre type de distribution de masse des partenaires QC. Et s'il y aura trois, ou quatre, ou cinq dimensions supplémentaires ... Peut-être bien plus de types de distributions.

Des exemples de certaines distributions de particules sans masse avec des tailles de mesures supplémentaires choisies de sorte que les masses des premiers partenaires KK soient les mêmes pour chaque cas sont donnés dans la Fig. 12. Il est évident que pour établir la forme et la taille des mesures supplémentaires, il est nécessaire de mesurer les masses d'un nombre suffisamment important de partenaires KK (et même au moins confirmer que l'une des particules lourdes nouvellement découvertes sont généralement des partenaires KK), par conséquent, afin de comprendre la nature de tout complément supplémentaire. mesures, le temps passera.


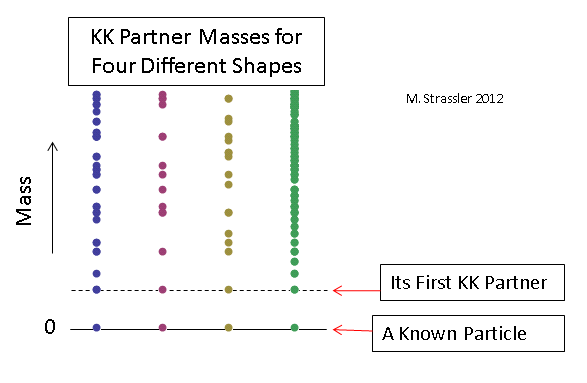Fig. 12

Mais les particules lourdes de matière connues peuvent-elles être des partenaires KK des plus légères?

Ensuite, la question supplémentaire évidente se pose.On sait que parmi les particules élémentaires connues il y a un électron, ainsi que ses versions plus lourdes: muon et tau. Il y a un quark supérieur, et ses versions plus lourdes sont enchantées et vraies. Il y a un quark inférieur, et ses versions plus lourdes, étranges et charmantes. Les versions à particules lourdes sont-elles les partenaires CQ des poumons?

À première vue, cette hypothèse est tentante, mais la réponse sera un non catégorique. Désolé.Ce n'est pas une question stupide. Il a juste une réponse négative intelligente.

Muon et tau, enchantés et vrais, étranges et charmants - ils obtiennent tous leur masse grâce au champ de Higgs, et non grâce à l'impulsion de dimensions supplémentaires. Cela découle clairement d'expériences détaillées. Des conseils peuvent être trouvés dans l'article sur ce qui se passerait si le champ Higgs était nul . Veuillez noter que si le champ de Higgs était nul en moyenne, alors l'électron, le muon et le tau n'auraient pas de masse (et chacun serait divisé en deux types de particules). Cela ne correspond pas à la théorie selon laquelle le muon et le tau sont des partenaires KK de l'électron.

Il y a bien d'autres raisons. Le plus grave d'entre eux sera peut-être qu'en raison de la présence d'une charge sur l'électron et du fait qu'il est entouré d'un champ électrique, le photon doit se déplacer dans n'importe quelle dimension dans laquelle l'électron se déplace (bien que l'inverse ne soit pas vrai). Donc, si l'électron a des partenaires KK, le photon devrait également les avoir. Mais il résulte de nos formules (et similaires plus généralisées) que puisque le photon n'a pas de masse, et que la masse électronique (0,0005 GeV / c ² ) est petite par rapport à la masse du muon (environ 0,1 GeV / c ²), si le muon est un partenaire KK, alors le photon doit avoir un partenaire KK de masse similaire. Mais une telle particule, si elle avait existé, aurait été découverte il y a de nombreuses années. En fait, les partenaires KK des photons n'ont pas été observés dans des expériences dans lesquelles des masses ont été étudiées beaucoup plus grandes que la masse de particules Z - ce sont plusieurs centaines de GeV / s ² . La particule Z elle-même ne peut pas non plus être un partenaire CQ d'un photon; elle ne lui ressemble pas assez. Et cela signifie que tout partenaire KK de l'électron devrait être au moins aussi lourd.

Où aller ensuite? Aux expériences

Nous sommes passés de la théorie (possibilité de mesures supplémentaires, mathématiques et géométrie associées) aux prédictions (partenaires QC). Prochaine étape: que savons-nous des mesures supplémentaires des expériences? Nous n'avons pas encore vu de partenaires KK dans les expériences, mais nous pouvons nous demander, que pouvons-nous apprendre de leur absence? Beaucoup, comme je l'expliquerai plus tard, avec une description de la façon dont les tentatives pour trouver des signes de mesures supplémentaires se poursuivent au Grand collisionneur de hadrons et ailleurs.