Notre univers est-il infini?
Attention! Dans cet article, seule une théorie sera exprimée, sans preuves scientifiques.
Bonjour Giktayms! J'ai été poussé à écrire cet article par une vidéo YouTube sur les paradoxes numériques inhabituels. A savoir, les paradoxes de
Zeno et pourquoi il est impossible de diviser par zéro, ce qui sera discuté aujourd'hui.
Le paradoxe de Zeno s'explique très facilement à partir d'
Achille et de la tortue. Ceux qui ne connaissent pas ce paradoxe, voici une vidéo visuelle d'un autre auteur:
Je vous recommande de lire avant de poursuivre la lecture.
(Paradoxe d'Achille et tortues)Si vous ne voulez pas regarder la vidéo, je vais vous dire brièvement: imaginez qu'Achille court après une tortue qui le rattrape. La distance entre eux diminue constamment, car Achille court plus vite qu'une tortue. Par conséquent, quand Achille approche une distance de 1 mètre, au bout d'un certain temps elle sera égale à
0,1 mètre, puis
0,01, et ainsi de suite à l'infini. Cela signifie qu'Achille ne rattrapera jamais la tortue, mais en réalité tout est complètement faux.
En réalité, il n'y a pas de problème, on prend Achille et la tortue, on la pose sur un tapis roulant et s'il vous plait, Achille dépasse calmement la tortue. C'est précisément en cela que réside la preuve possible que l'univers n'est pas infini.
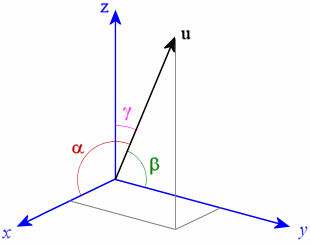(Vecteur dans l'espace 3D)Essayons d'expliquer cela sur le principe des jeux informatiques. En règle générale, la position d'un objet est écrite comme un vecteur composé des axes x, y et z. Et chaque valeur est stockée dans le type de données
float (valeur à virgule flottante) . Par exemple,
Unity3D utilise un flottant 32 bits pour indiquer sa position dans l'espace. La valeur minimale dont:
1,175494351 E - 38. , qui donne un mouvement fluide à presque n'importe quelle échelle. Ici, le mot important est
«presque» , c'est-à-dire que si nous réduisons et approchons considérablement le modèle, nous verrons comment il se déplace par sauts. Saut de
0, ... 1 à
0, ... 2 à
0, ... 3 , etc. Cela signifie que dans la simulation, dans n'importe quel scénario, Achille dépassera la tortue. Mais comme on dit, il n'y a pas de mal sans bien. Si nous avons une valeur flottante minimale, il y a pour ainsi dire une limite maximale de
l' espace
3D . Au-delà de cela, nous ne serons pas autorisés
(appelons-le) les lois de la physique du monde virtuel. En réalité, nous ne pouvons tout simplement pas donner plus que la valeur maximale d'une variable.
Si nous revenons au paradoxe de Zénon, Achille non seulement ne rattrapera jamais la tortue, mais n'atteindra jamais la frontière de son monde fantastique, pour lui ce sera infini. De -∞ à + ∞, curieusement, on obtient la même fonction
f (x) = 1 / x . Et le plus drôle est que la valeur
x / 0 ne tombe pas dans cette fonction, car la fonction n'atteindra jamais zéro, comme Achille la tortue.
(En fait, cela ne peut pas être divisé par zéro)Assez de théorie, passons à la pratique. Prenons le monde réel, nous sommes tous constitués d'atomes, les atomes sont constitués de protons neutroniques et d'électrons, eux-mêmes constitués de quarks
(particules élémentaires) . Dans la simulation et dans le monde réel, Achille n'a pas besoin de dépasser une tortue. Tout cela conduit au fait que, tant en simulation qu'en réalité, les particules élémentaires doivent également sauter par les nombres
0, ... 1 0, ... 2 0, ... 3 comme cela se produit dans le jeu, car Achille peut dépasser tortue ici et là. Cela nous indique que le paradoxe de Zénon ne fonctionne que sur papier, ou dans son système de coordonnées, dont la valeur est de -∞ à + ∞. En réalité, sautant aux plus petites valeurs, les particules élémentaires d'Achille dépassent à un moment donné la tortue, leurs coordonnées deviennent égales, après quoi Achille avance.
Nous avons donc appris quel système de coordonnées notre espace utilise, revenons au sujet principal. Si nous avons une valeur minimale, alors il y aura un maximum - le
bord de notre univers . Il y a ceux qui diront pourquoi alors, d'une part, il peut être infini, et d'autre part, fini. Mais le problème est que les coordonnées ou la position ne sont qu'un élément d'un grand système appelé espace, et elles peuvent être complètement infinies ou complètement finies. Aussi, tout cela pose la question, et par hasard nous ne sommes pas dans une simulation informatique, hein? Mais c'est un sujet pour un autre article.
Résumé
Donc, aujourd'hui, nous sommes arrivés à la conclusion que l'univers n'est
PAS infini, dans ce post, seule la théorie a exprimé comment personne ne connaît vraiment l'univers là-bas et ne peut pas le prouver. Mais peut-être qu'avec cet article, j'ai poussé quelqu'un à faire de nouvelles découvertes.
Source