Les équations de Navier-Stokes décrivent des phénomènes quotidiens simples, comme l'eau s'écoulant d'un tuyau d'arrosage, mais elles sont basées sur un problème dont la solution a été estimée à un million de dollars.

En physique, il existe des équations qui décrivent tout, de l'étirement de l'espace-temps au vol d'un photon. Cependant, un seul ensemble d'équations est considéré comme si mathématiquement complexe qu'il a été choisi comme l'un des sept "
problèmes du millénaire ", pour lesquels le
Clay Institute of Mathematics offre un prix d'un million de dollars: ce sont
les équations de Navier-Stokes décrivant l'écoulement des fluides.
Récemment, j'ai
écrit comment un nouveau résultat important a été obtenu pour ces équations. Et ce travail indique que les progrès vers le Prix du Millénaire seront plus difficiles que prévu. Pourquoi ces équations décrivant des phénomènes familiers comme l'eau s'écoulant à travers un tuyau sont-elles mathématiquement plus difficiles à comprendre que, par exemple, les équations du champ d'Einstein, qui incluent des objets aussi étonnants que des trous noirs?
Si je comprends bien, la réponse réside dans la turbulence. Nous avons tous vécu ce phénomène, en vol dans de l'air non homogène à une altitude de 10 000 m, ou en observant un entonnoir de l'eau sortant du drain dans le bain. Cependant, la connaissance ne découle pas de la conscience: la turbulence est l'un des domaines les moins bien compris du monde physique.
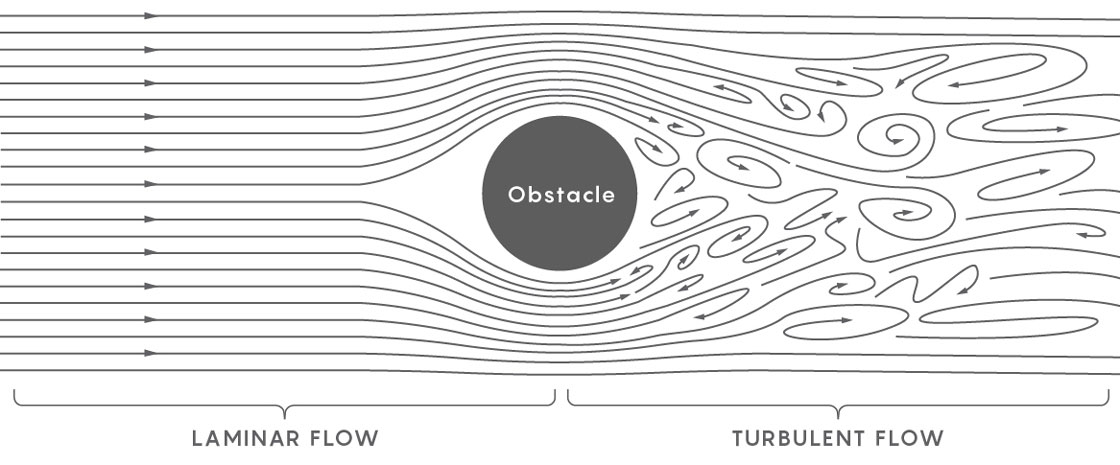
Un exemple d'écoulement sans turbulence est une rivière calme. Chaque partie se déplace dans la même direction à la même vitesse. Un fluide turbulent apparaît lorsque le ruisseau d'une rivière se brise, de sorte que différentes parties du ruisseau commencent à se déplacer dans différentes directions à différentes vitesses. Les physiciens décrivent la formation de turbulences d'abord comme l'apparition d'un entonnoir dans un écoulement régulier, puis comme la formation de petits entonnoirs dans le premier entonnoir, et même de plus petits entonnoirs dans ces entonnoirs - une mer d'entonnoirs qui entrent dans le liquide, de sorte que le liquide se brise en parties discrètes, chacune desquelles interagit les uns avec les autres et se déplace dans sa propre direction.
Les chercheurs veulent comprendre exactement comment un écoulement fluide se transforme en turbulence turbulente et modéliser la forme future du fluide une fois que la turbulence aura fait des ravages. Mais le Millennium Challenge est formulé de façon plus modeste: il suffit de prouver que les solutions existent toujours. Autrement dit, la question est de savoir si les équations peuvent décrire n'importe quel fluide, avec des conditions initiales et dans un avenir infiniment éloigné?
«La première étape consiste simplement à essayer de prouver que les équations ont des solutions», explique Charlie Fefferman, mathématicien à l'Université de Princeton. "Cela ne donne pas une réelle compréhension du comportement des liquides, mais si vous n'en avez pas non plus, alors vous ne savez rien du tout."
Alors, comment prouver l'existence de solutions? Vous devez commencer par comprendre pourquoi ils pourraient ne pas l'être. Les équations de Navier-Stokes impliquent le calcul de changements dans des quantités telles que la vitesse et la pression. Les mathématiciens s'inquiètent du scénario suivant: vous fuyez ces équations, et après un certain temps fini, elles vous disent qu'une particule fluide se déplace à une vitesse infinie. Et c'est le problème - calculer la variation de la valeur infinie n'est pas plus facile que de diviser par zéro. Les mathématiciens appellent de telles situations une «explosion», et en cas d'explosion, les équations cessent de fonctionner et aucune solution n'est trouvée.
 Les équations de Navier-Stokes décrivent l'écoulement d'un fluide incompressible.
Les équations de Navier-Stokes décrivent l'écoulement d'un fluide incompressible.
En général, le produit de la masse (partie bleue) et de l'accélération (violet) est égal aux forces agissant sur le liquide (orange):- ρ est la densité du fluide;
- dV / dt - changement de vitesse dans le temps;
- V ∇V - vitesse et direction du mouvement;
- ∇P - changement de pression interne;
- ρ g - l'influence des forces externes (par exemple, la gravité);
- μ ∇ 2 V - l'influence des forces internes (viscosité).
La preuve de l'absence d'explosions (et de l'existence de solutions) équivaut à la preuve que la vitesse maximale de toute particule liquide reste limitée par une valeur finie. L'une des quantités les plus importantes est l'énergie cinétique du liquide.
Lorsque vous commencez à simuler l'écoulement à l'aide des équations de Navier-Stokes, votre fluide a une certaine quantité initiale d'énergie. Dans les écoulements turbulents, l'énergie peut commencer à se concentrer. Au lieu de se répandre uniformément dans la rivière, l'énergie cinétique peut être collectée dans des tourbillons d'une taille arbitrairement petite, et les particules dans ces tourbillons (théoriquement) peuvent accélérer à une vitesse infinie.
«Avec la transition vers des échelles de plus en plus petites, l'énergie cinétique devient de moins en moins utile pour le contrôle des décisions. La décision peut tout faire et je ne saurai pas la contrôler », explique Vlad Vikol, mathématicien à l'Université de Princeton qui a écrit un nouveau travail avec Tristan Buckmaster.
Les mathématiciens classent les équations partiellement différentielles en fonction de la mesure dans laquelle elles peuvent commencer à se comporter mal à des échelles infiniment petites. Les équations de Navier-Stokes sont à l'extrémité extrême de cette échelle. La complexité des mathématiques des équations reflète en quelque sorte la complexité des écoulements turbulents qu'ils doivent être capables de décrire.
«Lorsque vous effectuez un zoom avant sur un endroit, puis d'un point de vue mathématique, vous perdez des informations sur la solution», explique Vikol. "Mais la turbulence devrait décrire exactement cela - le transfert d'énergie cinétique de grandes à des échelles toujours plus petites, donc cela vous demande vraiment de passer à l'échelle."

En parlant des propriétés mathématiques des équations physiques, il est naturel de se poser une question: ces arguments vont-ils changer la façon dont nous considérons le monde physique? Dans le cas des équations de Navier-Stokes et du problème du millénaire, la réponse sera à la fois «oui» et «non». Après près de 200 ans d'expérimentation, il est clair que les équations fonctionnent: le flux prédit par Navier-Stokes coïncide consécutivement avec le flux observé dans les expériences. Si vous êtes un physicien travaillant dans un laboratoire, cela peut vous suffire. Mais les mathématiciens doivent en savoir plus - ils veulent vérifier s'il est possible de suivre ces équations tout le long du chemin pour surveiller comment exactement le débit change d'un moment à l'autre (pour toute configuration initiale de fluide), et même pour attraper la source de turbulence.
«Le comportement des liquides est semé d'embûches», explique Fefferman. "Ces surprises sont en principe expliquées par les équations fondamentales qui contrôlent le flux de fluides, mais comment passer des équations qui contrôlent le mouvement d'un fluide à une description de la façon dont le fluide se déplace est un mystère."