Deux mathématiciens ont prouvé que dans certaines conditions extrêmes, les équations de Navier-Stokes donnent un non-sens
Les équations de Navier-Stokes à l'aide de plusieurs termes laconiques décrivent l'un des phénomènes les plus courants du monde physique: l'écoulement des fluides. Aujourd'hui, ces équations, remontant aux années 1820, sont utilisées pour tout décrire, des courants océaniques aux turbulences suivant un avion en passant par le flux sanguin vers le cœur.
Bien que les physiciens considèrent ces équations comme fiables, comme un marteau, les mathématiciens se méfient d'eux. Pour un mathématicien, le fait que ces équations semblent fonctionner ne signifie pas grand-chose. Ils ont besoin de la preuve que les équations sont exemptes d'erreur: que pour tout fluide et pour la prévision à long terme, distribuée dans le futur, les mathématiques des équations n'échoueront pas. Il n'a pas été facile de trouver une telle garantie. La première personne ou équipe qui peut prouver que les équations de Navier-Stokes fonctionneront toujours - ou fournir un exemple prouvant qu'elles ne fonctionnent pas - pourra recevoir une récompense pour la résolution de l'un des
problèmes du Millénaire , annoncée par
Clay's Mathematical Institute , et un million de dollars en addition [en 2017, une seule des sept tâches du millénaire (hypothèse de Poincaré) a été résolue par Gregory Perelman / env. trad.].
Les mathématiciens ont développé de nombreuses façons de résoudre ce problème. Le nouveau travail, publié en septembre, soulève de sérieuses questions quant à savoir si l'une des approches les plus populaires du problème, développée au fil des ans, peut réussir. Le travail, écrit par Tristan Buckmaster et Vlad Vikol de l'Université de Princeton, est le premier résultat montrant comment, dans certaines conditions, les équations de Navier-Stokes donnent une description contradictoire du monde physique.
"Nous essayons de comprendre certains problèmes inhérents à ces équations, et pourquoi les gens devront probablement les repenser", explique Buckmaster.
Le travail de Buckmaster et Wikol montre que si vous faites des hypothèses très approximatives lors de la résolution des équations de Navier-Stokes, elles commencent à ne pas avoir de sens: elles disent que le même fluide avec les mêmes conditions initiales peut venir dans deux ou plusieurs états différents. Il peut s'écouler d'une manière ou d'une manière complètement différente. Si c'est le cas, alors ces équations ne peuvent pas décrire de manière fiable le monde physique pour lequel elles ont été développées.
Équation des équations
Pour comprendre comment les équations peuvent se briser, imaginez un courant océanique. Dans son cadre, des flux locaux peuvent exister, grâce auxquels certaines de ses parties peuvent se déplacer dans une direction et à une vitesse, et d'autres dans une autre direction à une autre vitesse. Les flux locaux interagissent les uns avec les autres dans l'action mutuelle constante du frottement et de la pression de l'eau, qui déterminent son débit.
Les mathématiciens modélisent cette interaction à l'aide d'une carte vous informant des directions et des débits en tout point du fluide. Cette carte, appelée champ vectoriel, est un instantané de la dynamique interne d'un fluide. Les équations de Navier-Stokes prennent cette photo et la reproduisent sous forme de vidéo, expliquant à quoi ressemblera exactement le champ vectoriel à chaque instant ultérieur.
La carte des vents (windy.com) fonctionne d'une manière similaire à un champ vectoriel. À chaque point, le vent a une certaine direction et force.Ces équations fonctionnent. Ils décrivent l'écoulement des fluides de manière aussi fiable que les équations de Newton prédisent les positions futures des planètes; les physiciens les utilisent constamment et ils coïncident constamment avec les résultats des expériences. Cependant, les mathématiciens ont besoin de plus que d'une confirmation épisodique - ils ont besoin de la preuve que les équations ne sont pas brisées, que peu importe le champ vectoriel à partir duquel vous commencez et à quelle distance vous le reproduisez à l'avenir, les équations vous donneront toujours nouveau champ vectoriel unique.
C'est le thème du problème du millénaire, qui demande si les équations de Navier-Stokes ont des solutions (la solution, en fait, est un champ vectoriel) pour tous les points de départ à tous les moments. Ces solutions doivent garantir la direction et la force exactes du débit à chaque point du fluide. Les solutions qui fournissent des informations avec une résolution infiniment petite sont dites «fluides». Pour une solution fluide, chaque point du champ est associé à un vecteur, ce qui vous permet de vous déplacer "en douceur" autour du champ sans vous coincer aux points où le vecteur est absent - à un point à partir duquel vous ne comprendrez pas le mouvement ultérieur.
Les solutions lisses sont une représentation complète du monde physique, mais d'un point de vue mathématique, elles peuvent ne pas toujours exister. Les mathématiciens travaillant sur des équations comme celles-ci s'inquiètent de cette situation: vous exécutez les équations de Navier-Stokes et observez les changements dans le champ vectoriel. Après un certain temps fini, les équations vous indiquent qu'une certaine particule de fluide se déplace à une vitesse infinie. Vous aurez alors des problèmes. Les équations incluent la mesure des changements de propriétés telles que la pression, le frottement et la vitesse du fluide - dans le langage du jargon, ils prennent des dérivées de ces quantités - mais il n'est pas plus facile de prendre la dérivée d'une quantité infinie que de diviser par zéro. Donc si les équations donnent une valeur infinie, on peut dire qu'elles vous ont refusé, ou "explosé". Ils ne peuvent plus décrire les états ultérieurs de votre fluide.
Une telle «explosion» est la preuve que les équations manquent d'une description de certaines propriétés du monde physique qu'elles doivent décrire. "Peut-être que les équations ne couvrent pas tous les effets d'un vrai fluide, car dans un vrai fluide, nous ne nous attendons pas à une vitesse infinie des particules", explique Buckmaster.
La solution au problème du millénaire est soit de montrer que les équations de Navier-Stokes n'explosent jamais, soit de trouver les conditions dans lesquelles cela se produit. L'une des stratégies utilisées par les mathématiciens consiste à assouplir les exigences quant à la précision avec laquelle ces équations doivent décrire les solutions requises.
Perturbation du débit
Les équations de Navier-Stokes doivent décrire l'écoulement de tout fluide, avec toutes les conditions initiales, et étendre la description infiniment loin dans le futur. En essayant de prouver cette capacité, les mathématiciens «affaiblissent» parfois, c'est-à-dire qu'ils utilisent des descriptions approximatives des champs vectoriels décrivant un fluide. Mais cela pose des problèmes.
Idéalement, les mathématiciens veulent prouver que l'application des équations de Navier-Stokes à tout fluide continu et "lisse" produira un résultat unique.
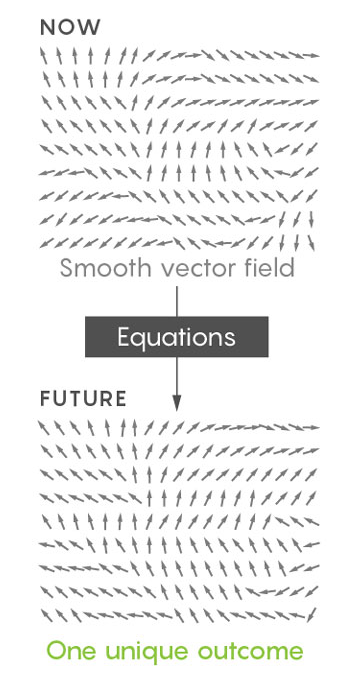
Cependant, il est plus facile de travailler avec des champs vectoriels «faibles», pas si détaillés. Et les mathématiciens ont découvert que certaines descriptions faibles produisent des résultats non uniques - elles permettent au même fluide de s'écouler dans les mêmes conditions initiales de deux manières.
De faible à lisse
Lorsque les mathématiciens étudient de telles équations, ils commencent parfois à élargir la définition de ce qui constitue une solution. Les solutions lisses nécessitent un maximum d'informations - dans le cas de Navier-Stokes, elles nécessitent qu'à chaque point du champ vectoriel associé au liquide un vecteur existe. Mais que se passe-t-il si nous assouplissons les exigences et disons que vous devez calculer des vecteurs uniquement pour certains points du champ, ou que vous devez obtenir uniquement des valeurs approximatives des vecteurs? De telles décisions sont qualifiées de «faibles». Ils permettent aux mathématiciens de ressentir le comportement de l'équation sans le travail fastidieux de trouver absolument toutes les solutions (ce qui en pratique peut ne pas être possible).
Tristan Buckmaster, mathématicien de l'Université de Princeton"D'un certain point de vue, les décisions faibles sont encore plus faciles à décrire que les vraies, car vous devez en savoir beaucoup moins", a déclaré Camillo De Lellis, co-écrit avec Lazlo Schekelikhidi, qui a écrit plusieurs ouvrages importants qui ont jeté les bases du travail de Buckmaster et Vikola.
Les solutions faibles existent en différents grades. Si vous imaginez une solution fluide sous la forme d'une image mathématique d'un liquide avec une résolution infinie, alors les solutions faibles seront quelque chose comme des versions 32 bits, 16 bits ou 8 bits de cette image.
En 1934, le mathématicien français
Jean Leray a défini une classe importante de solutions faibles. Au lieu de travailler avec des vecteurs exacts, les «solutions de Leray» prennent la valeur moyenne des vecteurs dans un petit voisinage du champ vectoriel. Leray a prouvé que vous pouvez toujours résoudre les équations de Navier-Stokes, permettant à vos décisions de prendre la forme de ce genre. En d'autres termes, les décisions de Lera n'explosent pas.
La réussite de Lera a déterminé une nouvelle approche du problème de Navier-Stokes: commencez par les solutions de Lera, dont l'existence est déjà connue, et voyez si vous pouvez les transformer en solutions fluides dont vous voulez prouver l'existence. Ce processus ressemble à celui où vous commencez avec une image approximative et voyez si vous pouvez progressivement tordre la résolution pour obtenir l'image parfaite de la réalité.
"L'une des stratégies possibles est de montrer que ces faibles décisions de Lera sont lisses, et si vous pouvez montrer qu'elles sont lisses, vous résoudrez le Millenium Challenge", a déclaré Bakmaster.
Vlad Vkol représente la moitié de l'équipe qui a révélé des problèmes dans l'approche de vérification des équations de Navier-Stokes.Il y a un autre hic. Les solutions des équations de Navier-Stokes correspondent à des événements physiques réels, et les événements physiques se produisent d'une manière possible. Compte tenu de cela, j'aimerais que vos équations n'aient qu'un seul ensemble de solutions uniques. Si les équations vous donnent plusieurs solutions possibles, elles ne peuvent pas faire leur travail.
Par conséquent, les mathématiciens ne pourront utiliser les solutions de Leray pour résoudre les problèmes du Millénaire que si les solutions de Leray sont uniques. Les solutions de Leray non uniques signifieront que, selon les règles de Navier-Stokes, le même fluide avec les mêmes conditions initiales peut arriver à deux états physiques différents, ce qui n'a pas de signification physique, et implique que les équations ne décrivent pas réellement ce qui devrait.
Le nouveau résultat de Bakmaster et Wikol est le premier indice que pour certaines définitions de décisions faibles, cela peut arriver.
De nombreux mondes
Dans leur nouveau travail, Buckmaster et Wikol envisagent des solutions encore plus faibles que les solutions de Leray - des solutions qui utilisent le même principe de moyenne que Leray, mais affaiblissent une exigence supplémentaire (connue sous le nom d'inégalité énergétique). Ils utilisent la méthode de «l'intégration convexe», issue des travaux sur la géométrie du mathématicien John Nash, et est ensuite impliquée dans l'étude des liquides par De Lellis et Schekelikhidi.
En utilisant cette approche, Buckmaster et Wikol prouvent que ces solutions très faibles des équations de Navier-Stokes ne sont pas uniques. Ils montrent par exemple que si vous commencez avec un liquide complètement calme, par exemple avec un verre d'eau à côté du lit, deux types d'événements sont possibles. La première est évidente: l'eau commence par un état calme et reste toujours calme. La seconde est fantastique, mais mathématiquement possible: l'eau part d'un état calme, explose au milieu de la nuit, puis revient à un état calme.
«Cela prouve le manque d'unicité, car au moins deux objets peuvent être construits à partir des données initiales», explique Vikol.
Buckmaster et Wikol ont prouvé l'existence de nombreuses solutions faibles non uniques (pas seulement les deux décrites ci-dessus) des équations de Navier-Stokes. L'importance de ces preuves reste à comprendre. À un certain point, les solutions faibles peuvent devenir si faibles qu'elles cessent d'être liées à des solutions plus lisses qui devraient imiter. Si tel est le cas, le résultat obtenu par Bakmaster et Wikol conduira à peu de choses.
«Ce résultat est clairement un avertissement, mais on peut affirmer que cet avertissement concerne l'idée la plus faible de décisions faibles. Il existe de nombreuses couches de solutions plus solides que vous pouvez espérer pour un comportement bien meilleur "dans le cas des équations de Navier-Stokes", explique De Lellis.
Le Backmaster et Wikol pensent également en termes de couches, et il a jeté son dévolu sur les décisions de Lehr - sur la preuve qu'ils admettent également plusieurs physiques dans lesquelles le même fluide du même état peut prendre différentes formes à l'avenir.
«Tristan et moi pensons que les décisions de Leray ne sont pas uniques. Nous n'avons pas encore prouvé cela, mais notre travail pose la tête de pont pour une attaque sur cette tâche », a déclaré Vikol.