Dans cet article, je parlerai du problème de sécurité de la technologie blockchain à la lumière de l'augmentation des performances des ordinateurs quantiques, je discuterai de certaines des méthodes de protection contre les attaques utilisant un ordinateur quantique, et d'un projet récent: Quantum-Resistant Ledger. Selon les développeurs, ce sera la première plate-forme au monde construite sur les principes du cryptage post-quantique et conçue pour fournir une protection contre le "choc quantique" en cas de développement rapide de ces technologies. Les plates-formes construites en utilisant les principes de chiffrement classiques peuvent être soumises à un tel coup. Sans changements fondamentaux, Bitcoin, Ethereum, Ardor et la plupart de ces plates-formes pourraient être dans un avenir proche.
Partie 1. Problème de sécurité
Vulnérabilité
L'algorithme de protection de Bitcoin et des systèmes similaires est basé sur le principe du chiffrement asymétrique avec des clés publiques et privées. Une transaction est signée avec une clé privée et sa validité est vérifiée à l'aide de la clé publique.
En utilisant des algorithmes d'attaque classiques, il est presque impossible de trouver une clé privée, connaissant la clé publique. Les systèmes de chiffrement asymétriques, tels que RSA et similaires (DSA, DH, etc.), sont basés sur l'affirmation que la complexité de la factorisation d'un nombre croît de façon exponentielle à partir de la taille de la clé. Cependant, en utilisant
l'algorithme Shore sur un ordinateur quantique, il devient possible en temps polynomial de décomposer le nombre en facteurs premiers et, ainsi, de trouver la clé privée, en connaissant la clé publique.
En 2001, IBM l'a
démontré en divisant le nombre 15 en deux facteurs premiers, 3 et 5. Un ordinateur quantique composé de 7 qubits a été utilisé à ces fins. Depuis lors, le développement des technologies de l'informatique quantique progresse plus rapidement.
En 2016, un groupe de chercheurs du Massachusetts Institute of Technology, conjointement avec l'Institut d'Innsbruck, effectue la même tâche de décomposition du nombre 15, en
utilisant seulement 5 qubits .
En juillet 2017, un
ordinateur programmable à 51 qubits a été créé par des physiciens russo-américains.
Fin octobre 2017, un groupe de recherche international des universités de Singapour et d'Australie est arrivé à la conclusion que la plupart des protocoles cryptographiques utilisés dans la blockchain sont vulnérables aux attaques d'un puissant ordinateur quantique. Le
rapport du groupe fournit 2 prévisions de la croissance de la puissance de l’ordinateur quantique: optimiste et moins optimiste. Selon le premier, le nombre de qubits d'un ordinateur quantique doublera tous les 10 mois. Une prévision moins optimiste indique un doublement du nombre de qubits tous les 20 mois. La figure ci-dessous montre des graphiques des deux prévisions.
Le plus vulnérable aux attaques informatiques quantiques est l'algorithme de création d'une signature numérique basée sur des courbes elliptiques (
ECDSA ). Ainsi, selon
le rapport du groupe , le Bitcoin sous sa forme classique pourrait être piraté d'ici 2027.
Peut-être que tout n'est pas si mauvais? La clé publique n'est pas stockée en texte clair
Fin avril 2017, un
article a été publié sur bitcoin.com pour répondre à la question de savoir si les détenteurs de Bitcoin devraient se garder de le casser avec un ordinateur quantique. Il indique que malgré le fait qu'un cryptage asymétrique est utilisé dans la blockchain Bitcoin, les utilisateurs ne devraient pas se soucier de la sécurité de leurs pièces. La clé publique n'est pas stockée en texte clair. Ainsi, les adresses de transfert de pièces ne sont pas des clés publiques, mais uniquement le résultat de l'application de la fonction de hachage SHA-256. La fonction de hachage effectue une conversion unidirectionnelle et est donc résistante aux attaques d'un ordinateur quantique.
La clé publique devient connue lors de la transaction
L'affirmation selon laquelle la clé publique n'est pas disponible en clair n'est pas entièrement vraie. Sans entrer dans les petits détails, nous analyserons à l'aide de l'exemple de Bitcoin (BTC) comment la crypto-monnaie est transférée d'une personne à une autre.
Laissez Alice dans son portefeuille sur l'une des adresses Bitcoin avoir 100 mBTC (1000 mBTC = 1 BTC). Elle veut transférer Bob 1 mBTC. Pour ce faire, elle indique l'adresse Bitcoin de Bob, les frais de transfert et l'adresse Bitcoin dans son portefeuille pour recevoir la monnaie. Supposons qu'Alice ait indiqué 1 mBTC comme commission. Ainsi, sur 100 mBTC qu'Alice possède, 1 mBTC est envoyé à Bob, 1 mBTC part en commission sur le réseau Bitcoin et 98 mBTC est retourné au portefeuille d'Alice.
Voyons maintenant ce qui se passe au niveau du réseau Bitcoin. Alice et Bob ont des portefeuilles contenant des adresses pour stocker des pièces. Un portefeuille peut contenir plusieurs adresses Bitcoin. Les adresses sont générées lors de la création de portefeuilles. Chaque adresse correspond à une paire de clés créée par l'algorithme ECDSA: publique et privée. Lors du transfert de pièces, une transaction est créée dans laquelle des informations sur le nombre de pièces transmises par Alice, l'adresse Bitcoin de Bob, une signature faite par la clé privée d'Alice,
la clé publique d'Alice et d'autres données sont transmises. Ensuite, la transaction
sous une forme ouverte (non cryptée) est envoyée au réseau . Les hôtes, avant d'accepter une transaction pour traitement, vérifient sa signature à l'aide de la clé publique. Si la signature est valide, ils ajoutent des informations de transaction au bloc. Cette opération de commutation est appelée confirmation.
Le temps moyen de génération de blocs dans le réseau Bitcoin est de 10 minutes. Le réseau cherche à maintenir ce temps constant. Avant d'utiliser les fonds reçus,
il est recommandé d' attendre 6 confirmations. Ainsi, Bob, en respectant les règles de sécurité, pourra utiliser les fonds reçus environ une heure après leur transfert.
L'une des caractéristiques du transfert de pièces sur le réseau Bitcoin est qu'il n'est pas possible de transférer uniquement une partie des pièces à partir d'une seule adresse. Les pièces sont toujours transférées en totalité, situées sur l'adresse Bitcoin du portefeuille, et la modification est retournée à l'expéditeur. Il peut être obtenu à l'adresse à laquelle les pièces ont été envoyées et à toute autre. Par conséquent, Alice doit indiquer l'adresse de livraison. Dans un certain nombre de logiciels exploitant le portefeuille, l'adresse de livraison est l'adresse d'envoi.
Des frais de transaction, à proprement parler, ne sont pas obligatoires, mais son absence peut retarder la transaction pendant longtemps. L'inverse est également vrai: vous pouvez accélérer quelque peu la transaction en augmentant le montant de la commission. Au moment d'écrire ces lignes (janvier 2018), la plupart des logiciels de portefeuille offrent des frais de 1 mBTC. Il existe un certain nombre de ressources, par exemple
celle-ci , qui vous permettent d'estimer le moment où une transaction est incluse dans un bloc en fonction de la taille de la commission.
Utilisation de la clé publique 1 fois
Du point de vue de la sécurité, il est préférable de recevoir la modification d'une nouvelle adresse, dont la clé publique ne sera pas connue du réseau. Dans ce cas, la paire de clés n'est utilisée qu'une seule fois. Cependant, selon les
statistiques de décembre 2017, environ 41,34% des adresses sont réutilisées.
10 minutes pour attaquer
Cependant, tôt ou tard, vous devrez utiliser les fonds à la nouvelle adresse. La clé publique est transmise au réseau en clair. Jusqu'à ce que la confirmation soit arrivée, les fonds sont toujours à l'expéditeur. Si un attaquant reçoit une clé publique lors d'une transaction, il disposera d'environ 10 minutes pour obtenir la clé privée à l'aide d'un ordinateur quantique et tenter de mener sa transaction à partir de la même adresse, en fixant une commission plus élevée.
Les adresses statiques sont plus vulnérables
Dans des systèmes tels que Ethereum, NXT, Ardor, etc., la clé publique devient également connue après la première transaction. La situation est aggravée par le fait que les jetons ou les contrats intelligents sont liés à des adresses statiques, qui peuvent être attaquées pendant longtemps. Si l'attaque réussit, l'attaquant pourrait détruire tout le système économique basé sur ces adresses.
Partie 2. Solutions
Comment offrir une résistance aux attaques d'un ordinateur quantique?
Actuellement, il existe plusieurs méthodes de base qui offrent une protection contre les attaques informatiques quantiques:
- cryptographie basée sur le hachage;
- cryptographie basée sur le code;
- cryptographie matricielle;
- cryptographie basée sur des systèmes quadratiques multidimensionnels;
- cryptographie à clé privée.
Avec des clés suffisamment longues et le respect des exigences de sécurité, ces méthodes de protection sont capables de résister à la fois aux attaques classiques et aux attaques utilisant un ordinateur quantique.
La plus étudiée est l'utilisation de signatures numériques basées sur des fonctions de hachage.
Comme mentionné précédemment, la fonction de hachage effectue une conversion de message unidirectionnelle. Le message est converti en une valeur de hachage d'une longueur fixe. L'utilisation d'une fonction de hachage d'une part devrait rendre inutile la recherche dans les messages pour obtenir une valeur de hachage similaire. En revanche, l'algorithme doit être résistant aux collisions: lorsque 2 messages différents correspondent à la même valeur de la fonction de hachage.
L'algorithme quantique de Grover peut être utilisé pour essayer de trouver une collision ou effectuer une attaque préliminaire pour trouver le message d'origine. Cela nécessitera
O ( 2 f r a c n 2 ) opérations. Ainsi, pour maintenir une sécurité de 128 bits, la longueur du hachage résultant est d'au moins 256 bits. En tant que telle fonction, SHA-256 peut être sélectionné.
Signature du lampadaire
Une option pour utiliser une fonction de hachage dans une signature numérique est la signature de Lamport. Il peut être construit sur la base de n'importe quelle fonction de hachage unidirectionnelle. La stabilité cryptographique de l'algorithme est basée sur la stabilité cryptographique des fonctions de hachage utilisées.
Schéma de signaturePour le message
M longue
m les clés sont générées. Tout d'abord, les clés privées sont générées par paires
S k longue
n , puis, à l'aide d'une fonction de hachage, les paires de clés publiques sont formées à partir de clés privées
P k . Le nombre de paires de clés privées et publiques est égal au nombre de bits dans le message d'origine.
Lors de la signature, un message est lu bit par bit, et, selon la valeur du bit courant, une des clés privées de la paire correspondante est sélectionnée. Les clés privées sélectionnées sont combinées en une signature. Ensuite, la signature résultante et
m des paires de clés publiques sont envoyées au destinataire.
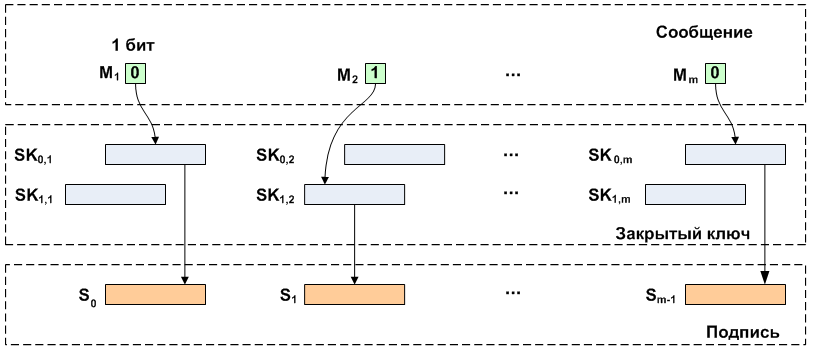
La vérification d'une signature est similaire au processus de création. La signature est divisée en fragments de longueur
n qui sont ensuite convertis en utilisant la même fonction de hachage. Le message est lu bit par bit et la valeur du bit sélectionne la clé publique, qui est comparée à la valeur de hachage reçue.
En règle générale, avant d'appliquer une signature, le message d'origine est haché pour réduire sa taille. Laissez SHA-256 être sélectionné comme fonction de hachage, puis
m=n=256 . Dans ce cas, la longueur totale de la clé publique (ainsi que privée)
LPK Il s'avère égal:
LPK=n∗2∗m=256∗2∗256=128Ko=16Ko.
Longueur de la signature
LS c'est:
LS=n∗m=64Ko=8Ko.
La signature de Lamport est unique (ne reste sûre qu'une fois utilisée), car lorsqu'elle est exécutée et transmise, la moitié de la clé privée devient connue. Laissez la longueur du message être 256 octets et la longueur du hachage 256. Avant qu'Alice ne publie la signature du message, personne ne connaît 2 * 256 nombres aléatoires dans une clé secrète. Ainsi, personne ne peut créer l'ensemble correct de 256 numéros pour la signature.
Une fois qu'Alice a publié la signature, personne ne connaîtra toujours les 256 numéros restants et ne pourra donc pas créer de signature pour les messages ayant un hachage différent.
Le fait que la signature de Lamport soit unique, combinée à une quantité totale impressionnante de signature et de clé publique (24 Ko avec une longueur de message de 256 octets et une longueur de hachage de 256 octets), rend son utilisation dans un bloc de transaction publique inappropriée.
Signature Winternitz
Il existe d'autres algorithmes de signature numérique uniques. Dans la signature de Vinternytsia, contrairement à la signature de Lamport, le message original est signé non pas au niveau du bit, mais en bloc. La signature unique de Winternitz, comme Lamport, peut être construite sur la base de toute fonction cryptographique forte.
Schéma de signatureMessage
M longue
m brisé en fragments
Mi longue
w . Une clé privée est générée pour chaque fragment
SK longueurs
n . Pour chaque clé privée, une opération de hachage est appliquée séquentiellement

fois (tours
R ) À la suite des opérations, les clés publiques correspondantes sont obtenues
PK même longueur
n .
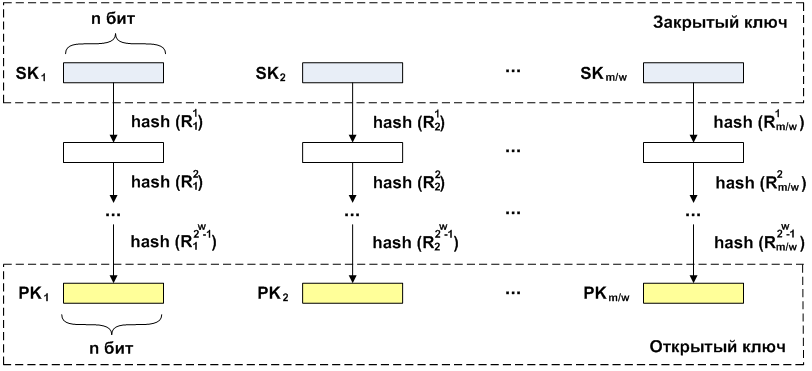
Lors de la signature, comme lors de la génération de clés publiques, un calcul itératif du hachage sur les clés privées est effectué. Le nombre de répétitions dans chaque cas dépend du message signé. Comme mentionné précédemment, le message est divisé en blocs de longueur
w . La valeur numérique de ce bloc
Mi et est le nombre d'itérations qui doivent être effectuées sur des clés privées pour obtenir une signature. La connexion des blocs reçus sera la signature de ce message.
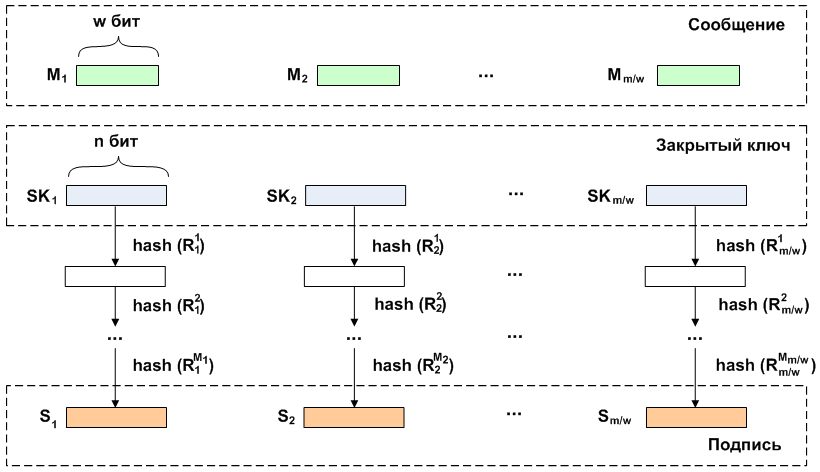
Lors de la vérification d'une signature sur des fragments de sa longueur
n calcule de manière itérative le hachage. Nombre de tours
Ri l'application de la fonction de hachage est définie comme la différence entre le nombre d'itérations pour obtenir la clé publique et la valeur numérique du bloc de message, c'est-à-dire
Ri=2w−1−Mi fois. Ensuite, les valeurs obtenues sont comparées avec la clé publique correspondante.
ExempleJe vais illustrer ce qui précède avec un petit exemple. Que le message soit donné
M (en représentation binaire) longueur
m , paramètre Vinternitsa
w et une fonction de hachage de la longueur
n :
M=1100011101100111,m=16,w=8,n=256.
Générer
m/w=2 clé privée basée sur un générateur de nombres pseudo aléatoires. Pour chaque clé privée que nous appliquons

fois une fonction de hachage, obtenant ainsi
2 clés publiques combinées en une seule clé de longueur commune

peu. Suivant pour chaque bloc de message
M longueurs
w déterminer le nombre d'opérations de hachage appliquées à la clé privée
Ri . Dans ce cas, ce seront les valeurs
110001112=19910 et

en conséquence. Après avoir effectué l'opération de hachage sur les clés privées, nous obtenons une signature de longueur

peu.
Pour vérifier la signature, divisez-la en parties de longueur
n . Nous produisons sur chaque pièce
Ri=2w−1−Mi opérations de hachage. C'est-à-dire

et

fois respectivement. Si le résultat des opérations aboutit à une valeur qui correspond à la clé publique, le message est fiable.
Lorsque vous utilisez SHA-256 comme fonction de hachage pour signer Winternitz,
m=n=256 .
Soit
w=8 peu. Ensuite, la taille complète de la clé publique
LPK et signatures
LS égal à:
LPK=LS=m/w∗n=256/8∗256=8Ko=1Ko.
Le nombre d'opérations de calcul de hachage dans ce cas est égal à:
P=(2w−1)∗m/w=(28−1)∗256/8=8160.
Pour le cas de
w=16 , cette valeur augmente jusqu'à
P=1048560 .
Les tailles de la clé publique et de la signature, avec les mêmes paramètres que dans l'exemple de la signature Lamport, sont de 1 Ko. Au total, c'est moins que dans la signature de Lamport (24 Ko). Cependant, le nombre de calculs de hachage dans ce cas est 8160. Ce qui, bien sûr, est beaucoup. De plus, lors de la vérification de la signature, une moyenne de la moitié de ce nombre d'itérations est effectuée. Cela rend cette option de signature inappropriée pour une utilisation sur la blockchain.
Il existe plusieurs options pour signer Winternitz, y compris avec l'extension de la signature afin d'augmenter la fiabilité et de réduire le nombre d'utilisations de la fonction de hachage. Leur description dépasse le cadre de cet article. Ceux qui sont intéressés peuvent en voir plus
ici . L'application de la signature Vinternitsa basée sur la fonction de hachage domestique de GOST 34.11-12 peut être vue
ici .
Merkle Tree (MSS)
Les signatures uniques peuvent fournir une sécurité cryptographique satisfaisante, cependant, c'est leur utilisation unique qui peut devenir un problème sérieux. Qu'il soit nécessaire de transférer les économies d'une adresse à une autre. Il s'avère que lors de l'utilisation de signatures uniques, il sera nécessaire de transférer le montant total des fonds à chaque fois, et pour chaque transaction, une nouvelle adresse sera nécessaire. Avec chaque transaction, vous devrez publier une nouvelle clé publique. De plus, le stockage de nouvelles transactions dans la blockchain nécessitera progressivement de plus en plus de temps pour les rechercher.
Pour résoudre le problème, ils développent le schéma de signature en effectuant plusieurs signatures basées sur plusieurs paires de clés pour chaque adresse. L'utilisation de plusieurs signatures est effectuée sur la base d'un arbre de hachage binaire - l'arbre Merkle.
Plus de détailsLe calcul d'un arbre se fait des feuilles à la racine. Chaque feuille de nœud de l'arbre est calculée comme un hachage à partir de la clé publique générée. Les nœuds restants sont calculés en obtenant un hachage à partir de la concaténation (collage) des nœuds enfants. Ainsi, l'arbre entier est calculé à la racine. Supposons qu'il existe 4 paires de clés, l'arbre Merkle est calculé en calculant 7 hachages (voir la figure ci-dessus).
Une caractéristique de l'arbre Merkle est que l'existence de n'importe quel nœud ou feuille peut être prouvée cryptographiquement en calculant la racine.
La signature du message est créée à l'aide de la clé privée de la paire de clés sélectionnée.
La vérification de signature implique de calculer la racine en fonction des paramètres transmis et de la comparer avec une clé publique réutilisable. Ces paramètres sont:
- signature
- racine
- clé unique, partie fermée dont le message a été signé;
- des hachages d'arbres le long du chemin de la feuille sélectionnée à la racine.
Lors de l'utilisation de signatures Merkle ou Winternitz uniques, il n'est pas nécessaire de transférer une clé publique unique sélectionnée séparément, car elle peut être obtenue à partir de la signature du message. Il suffit de passer son numéro, reflétant sa position dans l'arbre. , : , , — 0 (
PK1 )
H2 H6 .
PK1 , ,
H1 .
H1 H2 H5 .
H5 H6 R , .
L'arbre Merkle, compilé et calculé à partir des clés publiques, permet au lieu de publier l'ensemble de celles-ci de ne publier que la racine de l'arbre. Cela augmente la taille de la signature en incluant une partie de l'arborescence dans la signature, mais permet d'utiliser un seul hachage pour vérifier plusieurs signatures. Donc, avec la profondeur de l'arbreN peut être signé2 postes N. L'arbre Merkle pour les clés basé sur l'algorithme de courbe elliptique est utilisé dans Bitcoin et Ethereum, il y a un excellentarticlesur ce dernier avec un examen de l'arbre Merkle.Hypertrees
Le principal inconvénient du schéma de base de Merkle est que le nombre de signatures disponibles est limité et que toutes les paires de clés de signatures à usage unique doivent être générées avant le calcul de l'arborescence Merkle. La génération de clés et le temps de signature augmentent de façon exponentielle par rapport à la hauteur des arbres. Il est possible de retarder la génération de nouvelles clés, ainsi que d'augmenter le nombre de paires disponibles, lors de l'utilisation d'un hyper arborescence.Plus de détails, . 2 : . , . . , (. ).
, , . , , . , .
. . , , .
Structure d'arbre Merkle étendue (XMSS)
Une description complète du circuit va bien au-delà de la portée de cet article; plus de détails peuvent être trouvés ici . Je ne parlerai que des concepts et caractéristiques de base. Le schéma XMSS, comme l'arborescence Merkle, vous permet d'étendre les signatures uniques. L'utilisation d'un masque binaire utilisant des OU exclusifs (XOR) des nœuds enfants avant que les hachages ne soient concaténés au nœud parent augmente la résistance aux collisions des fonctions de hachage utilisées. Ainsi, lorsque vous utilisez SHA-256 comme fonction de hachage en combinaison avec un schéma étendu, Winternitz avec un paramètre de sécurité (W-OTS +) vous permet d'augmenter la sécurité de 128 à 196 bits. Selon lenstraLa défense de 196 bits est suffisante pour être considérée comme sûre contre les attaques par une simple attaque par force brute jusqu'en 2169. Avec tous les avantages du schéma XMSS, son principal inconvénient est le long temps de génération de clé.Actuellement, il existe d'autres schémas d'extension d'arbre Merkle ( GMSS , CMSS ) qui, en combinaison avec des algorithmes de signature à usage unique, peuvent également être utilisés dans une blockchain qui résiste aux attaques utilisant un ordinateur quantique.Partie 3. Réalisation des idées
Projet de blockchain durable quantique - QRL
Au second semestre 2016, le Dr P. Waterland a créé un groupe pour développer une blockchain stable à la fois pour les attaques classiques et pour les attaques utilisant un ordinateur quantique. Selon les résultats de l'élaboration de la partie théorique à la fin de la même année, le document principal de la blockchain développée, le «livre blanc» (livre blanc), a été rendu public. Le document est actuellement disponible en plusieurs langues, dont le russe.Caractéristiques clés de QRL
1. Schéma de signature et sécuritéUn schéma de signature est appliqué sur la base de l'algorithme de signature étendu de Winternitz (W-OTS +, w = 16, SHA-256) basé sur des structures connectées XMSS. Cette approche vous permet de générer des adresses avec la possibilité de signer, en évitant le long délai de calcul observé lors de la création de constructions XMSS géantes. Fournit une protection de 196 bits avec une sécurité prévisible contre les attaques par simple énumération jusqu'en 2169.
2. Algorithme de consensus - preuve de travailLors de la première itération du réseau principal, un algorithme de consensus de preuve de travail a été annoncé.
3. Commission flottanteDes transactions plus importantes que les autres blocs de la chaîne de transactions nécessitent un paiement pour chaque transaction. Selon Waterland, les marchés avec une commission artificielle (par exemple, Bitcoin) ne sont pas nécessaires et contredisent l'idéal d'une blockchain ouverte. Chaque transaction, si elle est accompagnée d'un paiement minimum, doit être aussi valable que toute autre. Le montant minimum de paiement acceptable pour les mineurs devrait être flottant et fixé par le marché. C'est-à-dire les nœuds (mineurs) doivent établir de manière compétitive une frontière inférieure pour le paiement entre eux. La valeur minimale absolue sera respectée au niveau du protocole. Ainsi, les mineurs commanderont des transactions de la mempool pour les inclure dans le bloc à leur discrétion.
4. Calcul de récompense de bloc dynamiqueChaque bloc nouvellement créé inclura la première transaction de coinbase contenant l'adresse de minage, pour laquelle la récompense sera définie comme le montant de la récompense pour le taux de la pièce avec le montant total des commissions pour les transactions dans le bloc.
5. Le temps passé par les blocs est de 1 minuteLe temps entre les blocs du réseau Bitcoin est d'environ 10 minutes. Avec les 6 confirmations requises, cela augmente en outre le temps d'attente pour l'achèvement de la transaction. Les nouveaux schémas de blocs de chaîne de transactions, tels que Ethereum, sont améliorés sous cet aspect et bénéficient d'un temps de bloc plus court sans perte de sécurité ni centralisation des mineurs en raison du taux élevé d'apparition de blocs orphelins / obsolètes.
Pour QRL, ce temps de blocage est de 1 minute.
6. Taille du bloc adaptatifPour éviter d'éventuels litiges, une solution adaptative prête à l'emploi a été modélisée sur la base de la proposition Bitpay, qui utilise un multiplicateur pour augmenter la taille du bloc
x taille moyenne
y le dernier
z blocs. L'utilisation d'une valeur moyenne ne permet pas aux mineurs de manipuler, y compris des blocs vides ou débordés pour modifier la taille moyenne des blocs.
x et
z alors il y aura des règles de consensus strictes pour le réseau qui devront obéir. Ainsi, la taille maximale du bloc
b peut simplement être calculé comme:
b = x y .
7. Monnaie - quantiqueL'unité monétaire de base est un quantum. Chaque quantum est divisé en les plus petits éléments. Voici les noms de tous les éléments dans l'ordre croissant:
| Objet | Valeur |
|---|
| Rive | 1 |
| Nakamoto |  |
| Buterin |  |
| Merkle |  |
| Lampport |  |
| Quantum |  |
Ainsi, chaque transaction impliquant une partie du quantum est en fait un très grand nombre d'unités Shore. Les frais de transaction sont calculés et affichés en unités Shore.
8. Comptes et adressesLes soldes des utilisateurs sont stockés sur des comptes. Chaque compte est une adresse de bloc de chaîne de transaction unique et réutilisable, indiquée par une ligne commençant par «Q».
L'adresse est créée en exécutant SHA-256 à la racine Merkle de l'arbre de certification XMSS le plus élevé. À cela s'ajoute une somme de contrôle de quatre octets, formée des quatre premiers octets du double hachage SHA-256 de la racine Merkle et de la lettre «Q».
Par exemple, dans le pseudo-code Python, cela sera décrit comme suit:
Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]
Adresse de compte typique:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479
Chaque compte a un solde, libellé en quanta, divisible jusqu'à une seule unité Shore. Les adresses de chaque transaction utilisent une nouvelle paire de clés de signature à usage unique. Un compteur de transactions appelé nonce s'incrémente à chaque transaction envoyée depuis votre compte. Cela permet aux portefeuilles qui ne stockent pas toute la chaîne de blocs de suivre leur emplacement dans le schéma de signature hypertree avec conservation de l'état.
État actuel du projet et plans pour l'avenir
Après la publication du "livre blanc", le groupe a été reconstitué avec plusieurs nouveaux développeurs et les travaux ont commencé sur la mise en œuvre du plan. Des rapports d'avancement réguliers sont apparus sur le site Web du projet. Et en avril 2017, le réseau de test de la blockchain QRL avait déjà été lancé. Le code source du projet est publié sur Github. Le projet est activement discuté chez Bitcointalk et Reddit.
En mai 2017, une ICO a été réalisée dans l'écosystème Ethereum. Emission du jeton ERC20 QRL. Au total, 65 millions de jetons ont été émis. Parmi ceux-ci, 52 millions de jetons sont en circulation. En 200 ans, 40 millions de pièces supplémentaires seront émises progressivement. Ainsi, le volume total d'émission sera de 105 millions de pièces. Lorsque le réseau principal est lancé, ces jetons peuvent être échangés contre des pièces QRL dans un rapport 1: 1. Actuellement, les jetons sont disponibles à l'achat sur des bourses telles que Bittrex, Upbit et Liqui. Les cotations QRL, selon le site
coinmarketcap.com , sont présentées dans les figures ci-dessous.
Le lancement du réseau principal est prévu pour février-mars 2018.
À l'avenir, il est prévu de changer l'algorithme de consensus de la confirmation du travail à la confirmation de la mise (preuve de la mise). Le temps de séjour sûr prévu des blocs sera de 15 à 30 secondes.
Conclusion
Le progrès des technologies quantiques a été lancé et ne peut pas être arrêté. Au fur et à mesure que des machines quantiques de plus en plus productives apparaissent, la gamme de tâches qu'elles résolvent ne cesse de croître. Le piratage d'une défense cryptographique existante, non adaptée aux attaques d'un ordinateur quantique, a longtemps été l'un des sujets centraux de nombreux
forums de sécurité .
QRL est la première technologie blockchain conçue pour résoudre ce problème. À l'avenir, bien sûr, d'autres apparaîtront. Lequel d'entre eux sera le plus réussi - le temps nous le dira.
Remerciements
L'auteur est reconnaissant à
kamnik d' avoir préparé une partie importante du matériel, et en particulier à la partie technique, ainsi qu'à
SannX pour ses critiques et corrections constructives.
Les références
- Algorithme de rivage .
- Factorisation première sur un ordinateur quantique (IBM) .
- Factorisation du nombre 15 en facteurs simples sur un ordinateur quantique (MIT) .
- Rapport d'expériences sur un ordinateur 51 qubit .
- Rapport de l'International Research Group sur la stabilité du Bitcoin devant un ordinateur quantique .
- Utilisation de l'algorithme de génération de clés ECDSA dans la blockchain Bitcoin .
- À propos de la résilience de Bitcoin aux attaques informatiques quantiques .
- Confirmation de transaction sur le réseau Bitcoin .
- Informations sur les commissions sur le réseau Bitcoin .
- Statistiques de réutilisation des adresses Bitcoin .
- Algorithme Quantum Grover .
- Signature étendue Winternitz .
- Application d'une signature unique Vinternitsa basée sur la fonction de hachage de GOST 34.11-12 .
- Geektimes sur Ethereum .
- Schéma XMSS .
- Lenstra. Le choix des tailles de clés cryptographiques .
- GMSS
- CMSS .
- Cours sur les systèmes de crypto-monnaie .
- Forum annuel sur la sécurité post-quantique .
Matériel supplémentaire
- Un ordinateur quantique est-il dangereux pour Bitcoin ?
Projet QRL
- Site du projet .
- Livre blanc .
- Présentation
- Le blog .
- Code source de GitHub .
- Fil de discussion sur Bitcointalk .