Les physiciens ont l'intention de classer toutes les phases de la matière

Une classification complète peut conduire à un grand nombre de nouveaux matériaux et technologies. Cependant, les phases les plus exotiques continuent de résister à la compréhension des scientifiques

Au cours des trois dernières décennies, les experts en physique de la matière condensée ont découvert tout un merveilleux pays de nouvelles phases exotiques de la matière: des états collectifs de particules en interaction apparaissant soudainement complètement différents des états solides, liquides ou gazeux de la matière connus de tous.

Ces phases, comme certains l'ont compris dans les laboratoires, et certaines basées sur des calculs théoriques, apparaissent lorsque la matière refroidit presque à une température de zéro absolu, qui est plus de deux cents degrés en dessous du point de congélation de l'eau dans des conditions ordinaires. Dans ces conditions froides, les particules peuvent interagir de manière à leur faire rejeter toute trace de leur ancienne identité. Les expériences des années 1980 ont découvert que dans certaines situations, les électrons sont séparés en fractions de particules qui peuvent laisser des traces dans l'espace-temps sous forme de tresses ; dans d'autres, des versions sans masse d'eux-mêmes apparaissent parmi eux. Un réseau d'atomes en rotation devient liquide à partir de boucles en rotation ou de chaînes de ramification; les cristaux qui ne conduisaient pas l'électricité au départ commencent à passer du courant sur la surface. L'une des phases qui a choqué les experts, lorsqu'elle a été prouvée mathématiquement pour la première fois en 2011 , comprend des entités très étranges, des « fractons » qui s'engrènent les uns aux autres dans des motifs fractals [selon Wiki, les fractons sont un analogue fractal des phonons , quanta du mouvement vibratoire des atomes cristal / env. trad.].

Désormais, des équipes de recherche de Microsoft et d'autres sociétés sont en concurrence pour écrire des informations quantiques dans des pigtails et des boucles de certaines de ces phases afin de développer un ordinateur quantique. Pendant ce temps, les théoriciens de la physique de la matière condensée (CS) ont récemment mené plusieurs études qui sont les plus importantes pour comprendre les schémas de comportement collectifs afin de numéroter et de classer toutes les phases possibles de la matière. S'ils réussissent à établir une classification complète, cela permettra non seulement de décrire toutes les phases de la matière vues dans la nature dans la nature, mais aussi d'indiquer potentiellement la manière d'obtenir de nouveaux matériaux et technologies.

Les chercheurs, dirigés par des dizaines de meilleurs théoriciens et avec l'aide de mathématiciens, ont déjà classé toute une voiture de phases capables d'apparaître dans une ou deux dimensions spatiales , en les reliant à la topologie: aux mathématiques qui décrivent les propriétés immuables de formes telles qu'une sphère ou un tore. Ils ont également plongé dans la jungle des phases nées dans la région du zéro absolu dans la matière tridimensionnelle.


Xi Chen, théoricien de la matière condensée au California Institute of Technology

Les scientifiques recherchent «pas une loi spécifique de la physique», a déclaré Michael Zaletel , théoricien de la FCC à l'Université de Princeton. «Ils recherchent un espace de toutes les possibilités, et c'est en quelque sorte une idée plus profonde et plus belle.» Cela peut être inattendu, mais, comme le dit Zaletel, l'espace de toutes les phases cohérentes est lui-même un objet mathématique «avec une structure incroyablement riche qui, selon nous, dans un monde unidimensionnel et bidimensionnel, une en une coïncide avec ces belles structures topologiques» .

Il y a une «économie des options» à travers le paysage de toutes les phases », a déclaré Ashvin Vishwanath de l'Université de Harvard. «Et tout cela semble connaissable» - une telle chance le laisse perplexe. La numérotation des phases de la matière pourrait se révéler être quelque chose "comme la collecte de timbres", a déclaré Viswanath, "chacun est légèrement différent des autres, et il n'y a aucun lien entre eux." Au lieu de cela, la classification des phases ressemble plus à un «tableau périodique». Il contient de nombreux éléments, mais ils sont divisés en catégories et nous pouvons comprendre ces catégories. »

La classification du comportement manifeste des particules peut ne pas sembler si fondamentale, mais certains experts, par exemple, Xiao-Gang Wen du Massachusetts Institute of Technology, disent que les nouvelles règles des phases manifestes montrent comment les particules élémentaires elles-mêmes peuvent se produire dans le contexte de ils sont basés sur un réseau d'informations quantiques enchevêtrées, que Ven appelle «l'océan des qubits». Par exemple, dans la phase " fluide de réseau de cordes ", qui peut se manifester dans un système tridimensionnel de qubits, les perturbations ressemblent exactement aux particules élémentaires connues. «Un véritable électron et un vrai proton ne peuvent être que des fluctuations dans le réseau de cordes», explique Ven.

Nouvel ordre topologique

Avant que ces phases n'apparaissent soudainement à température nulle, les physiciens pensaient que toutes les phases leur étaient déjà connues. Dans les années 1950, ils pouvaient déjà expliquer ce qui se passe, par exemple, lorsque l'eau se transforme en glace, la décrivant comme une violation de la symétrie: si l'eau liquide a une symétrie de rotation au niveau atomique (c'est la même chose dans toutes les directions), alors les molécules de glace H ₂ O sont enfermés dans des colonnes et des lignes.

Tout a changé en 1982 après la découverte de l' effet Hall quantique fractionnaire , qui se manifeste dans un gaz d'électrons ultra-froid bidimensionnel. Une substance dans cet état possédait des particules manifestes avec des charges dans une fraction des charges d'un électron, faisant des fractions d'étapes dans un contournement unilatéral du périmètre du système. "En utilisant la symétrie, il était déjà impossible de distinguer entre ces phases", a déclaré Ven.

Un nouveau paradigme était nécessaire. En 1989, Ven a présenté que des phases telles que l'état de l'effet Hall quantique fractionnaire n'apparaissent pas sur le plan, mais sur d'autres ensembles topologiques - des surfaces connectées comme la surface d'une sphère ou d'un tore. La topologie fait référence aux propriétés globales et immuables de ces espaces qui ne peuvent pas être modifiées par une déformation locale. Comme vous le savez, au moins pour les topologues, vous pouvez transformer un beignet en une tasse en déformant sa surface, car les deux figures ont un trou, et, par conséquent, elles sont topologiquement équivalentes. Mais étirez et serrez autant que vous le souhaitez, et même le beignet le plus flexible ne peut pas être transformé en bretzel.

Ven a découvert que dans de nouvelles conditions topologiques de nouvelles propriétés apparaissent à des phases de température nulle, et a inventé le terme « ordre topologique », qui décrit l'essence de ces phases. D'autres théoriciens ont également découvert un lien entre les phases et la topologie. Avec la découverte de nombreuses phases exotiques différentes - il y en a tellement que les chercheurs disent qu'elles peuvent à peine les suivre - il est devenu clair que la topologie et la symétrie offrent un bon système pour les organiser.

Les phases topologiques n'apparaissent que dans la région du zéro absolu, car ce n'est qu'à ces basses températures que les systèmes de particules peuvent entrer dans l' état quantique fondamental avec l'énergie la plus faible. À l'état fondamental, des interactions délicates qui établissent l'identité des particules - disparaissant à des températures élevées - lient les particules aux systèmes globaux en utilisant l'intrication quantique. Au lieu de décrire les particules individuellement, elles deviennent mathématiquement des composants d'une fonction plus complexe qui les décrit toutes à la fois, souvent avec l'avènement de nouvelles particules sous la forme d'excitations de phase globale. Les schémas émergents d'enchevêtrement à longue distance s'avèrent être topologiques, c'est-à-dire insensibles aux perturbations locales - comme le nombre de trous dans un ensemble.


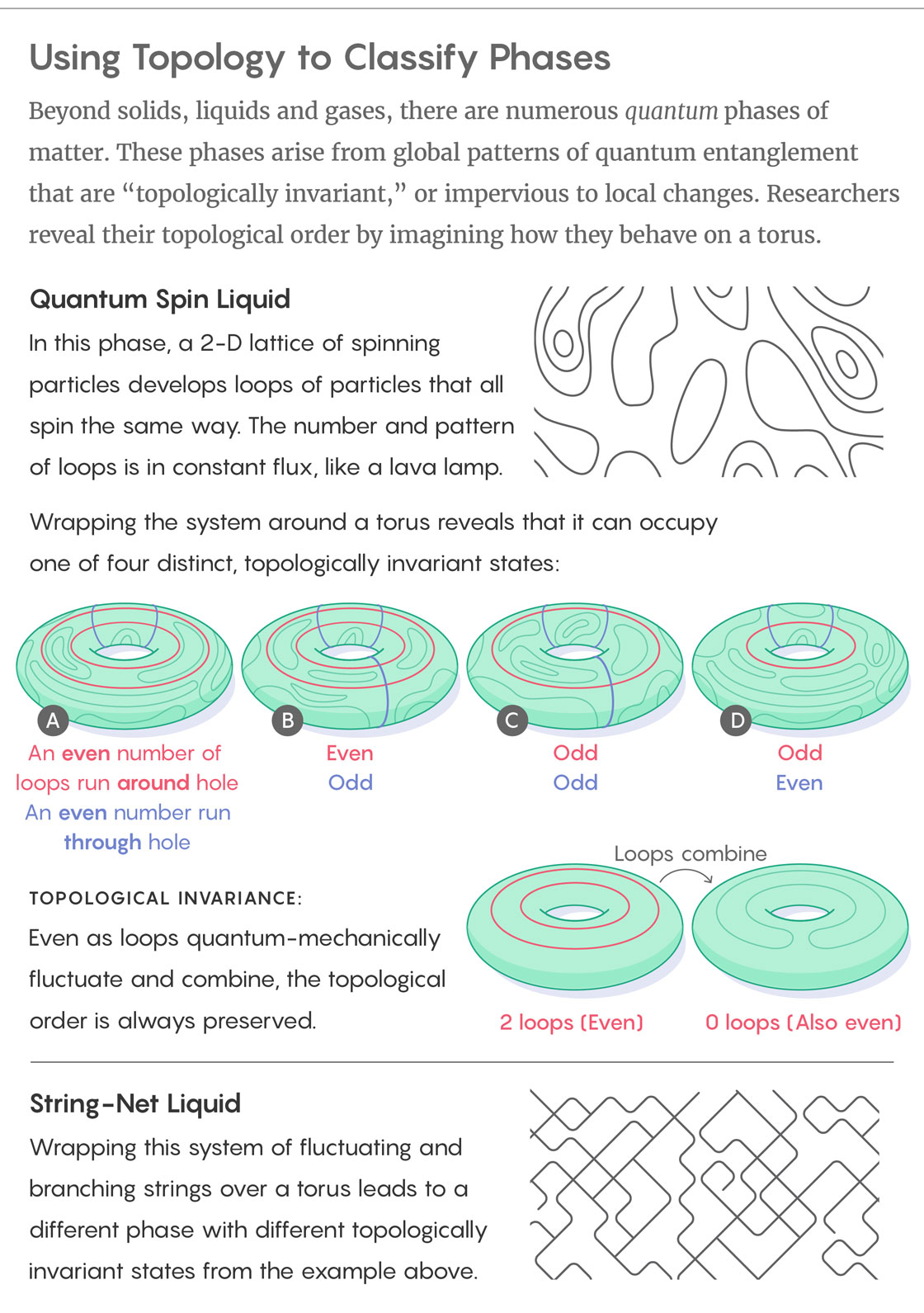Ci-dessus: phase de spin liquide quantique. Dans cette phase, un réseau bidimensionnel de particules en rotation conduit à l'apparition de boucles de particules tournant également. Le nombre et la disposition des boucles changent tout le temps, et tout cela ressemble à une lampe à lave .

Si vous enroulez ce système sur un tore, il s'avère qu'il peut occuper quatre états différents, topologiquement invariants:
A) Autour du trou: nombre pair de boucles / Trou traversant: nombre pair de boucles.
B) Pair / Impair.
C) Impair / Impair.
D) Impair / Pair.

Malgré le fait que les boucles subissent constamment des fluctuations quantiques-mécaniques, l'ordre topologique est toujours préservé (2 boucles peuvent aller à 0 boucles, ce qui est également un nombre pair).

En bas: fluide de réseau de chaînes. Si nous enveloppons un tore avec un système de chaînes changeantes et ramifiées, nous obtiendrons également divers états topologiquement invariants.

Considérons la phase topologique la plus simple d'un système appelé «liquide de spin quantique», consistant en un réseau bidimensionnel de spins, ou des particules pointant vers le haut, vers le bas ou, avec une certaine probabilité, simultanément dans les deux directions. À température nulle, le spin-liquide génère des chaînes de spins pointant dans une direction vers le bas, et ces chaînes forment des boucles fermées. La direction des spins est sujette aux fluctuations de la mécanique quantique, et le motif des boucles sur le matériau change également: les boucles des spins inférieurs sont combinées en plus grandes boucles ou divisées en plus petites. Dans une telle phase d'un fluide de spin quantique, l'état fondamental du système est une superposition quantique de tous les motifs de boucle possibles.

Pour comprendre pourquoi ce schéma d'enchevêtrement est un ordre topologique, imaginez comment Ven l'a fait, que le liquide des spins quantiques déborde sur la surface d'un tore, et que certaines boucles se tordent autour de son ouverture. Pour cette raison, au lieu d'obtenir un état fondamental associé à une superposition de tous les motifs de boucle, un fluide de spin existera dans l'un des quatre états fondamentaux différents associés à quatre superpositions de motifs de boucle. Un état se compose de tous les modèles de boucles possibles avec un nombre pair de boucles entourant le trou du tore et avec un nombre pair de boucles qui le traversent. L'autre a le premier nombre pair et le deuxième impair; les troisième et quatrième ont ces nombres, respectivement, impair / pair et impair / impair.

Et une fois dans l'un de ces états, le système y reste, malgré le fait que le modèle de boucle change localement tout le temps. Si, par exemple, le fluide de spin a un nombre pair de boucles entourant le trou du tore, alors ces deux boucles peuvent se toucher et se rejoindre et se transformer soudainement en une boucle qui n'entoure pas du tout le trou. Le nombre de boucles est réduit de deux, mais reste encore uniforme. L'état fondamental du système est une propriété topologiquement invariante qui résiste aux changements locaux.

Les ordinateurs quantiques du futur peuvent profiter de cette invariance. Si vous avez quatre états fondamentaux topologiques qui sont indépendants des perturbations ou des erreurs locales, "vous aurez un moyen de stocker des informations quantiques, car votre bit peut indiquer dans quel état vous êtes", explique Zaletel, qui a étudié les propriétés topologiques des liquides de spin et d'autres phases quantiques. Les systèmes tels que le fluide de rotation n'ont pas besoin de s'enrouler autour d'un tore pour avoir des états fondamentaux protégés topologiquement. Le bac à sable préféré des chercheurs est le « code toroïdal », une phase théoriquement construite par le théoricien de la FCC Alexei Kitaev du California Institute of Technology en 1997 et démontrée par des expériences au cours des dix dernières années. Un code toroïdal peut exister sur un plan et supporter encore plusieurs états de base inhérents à la surface d'un tore. En fait, les boucles de rotation peuvent se déplacer d'un bord du système et apparaître sur l'autre bord, et les boucles torsadées autour du système sont équivalentes aux boucles autour du trou de tore. "Nous savons comment établir des connexions entre les propriétés des états fondamentaux du système sur le tore et le comportement correspondant des particules", a déclaré Zaletel.

Les fluides de spin peuvent être dans d'autres phases, dans lesquelles les spins ne forment pas des boucles fermées, mais se ramifient et forment un réseau de chaînes. Il s'agit d'une phase liquide en réseau à cordes qui, selon Vienne, «peut donner l'ensemble du modèle standard» de la physique des particules, à commencer par un océan tridimensionnel de qubits.

Univers de phases

Des études menées par plusieurs groupes en 2009 et 2010 ont complété la classification des phases «isolées» de la matière qui se forment dans une seule dimension - les chaînes de particules. La phase isolée est à l'état fondamental: cet état basse énergie est suffisamment éloigné des états haute énergie pour que le système s'installe de manière stable dans cet état. Ce n'est que dans les phases quantiques isolées que des excitations bien définies sous forme de particules apparaissent. Les phases non séparées bouillonnent les soupes quantiques, leurs propriétés restent pour la plupart inexplorées.

Pour une chaîne unidimensionnelle de bosons - des particules comme des photons, avec un spin quantique entier (ce qui signifie qu'ils retournent à leur état d'origine après avoir changé de place), il n'y a qu'une seule phase topologique isolée. Dans cette phase, étudiée pour la première fois par le théoricien de Princeton Duncan Haldein , qui a reçu le prix Nobel pour des décennies de travail sur les phases topologiques en 2016 avec David Thowless et John Michael Kosterlitz, une chaîne de spin produit des particules avec un spin demi-entier aux deux extrémités. La chaîne de fermions a deux phases topologiques distinctes (ce sont des particules comme des électrons et des quarks, avec des spins demi-entiers - ce qui signifie que lorsque les positions sont modifiées, leur état devient négatif). L'ordre topologique dans ces chaînes unidimensionnelles ne se développe pas à partir de l'intrication à longue distance, mais de la symétrie locale reliant les particules voisines. Ces phases sont appelées «phases topologiques protégées symétriquement» et correspondent à des «cocycles de groupes cohomologiques », objets mathématiques associés à des invariants tels que le nombre de trous dans l'ensemble.


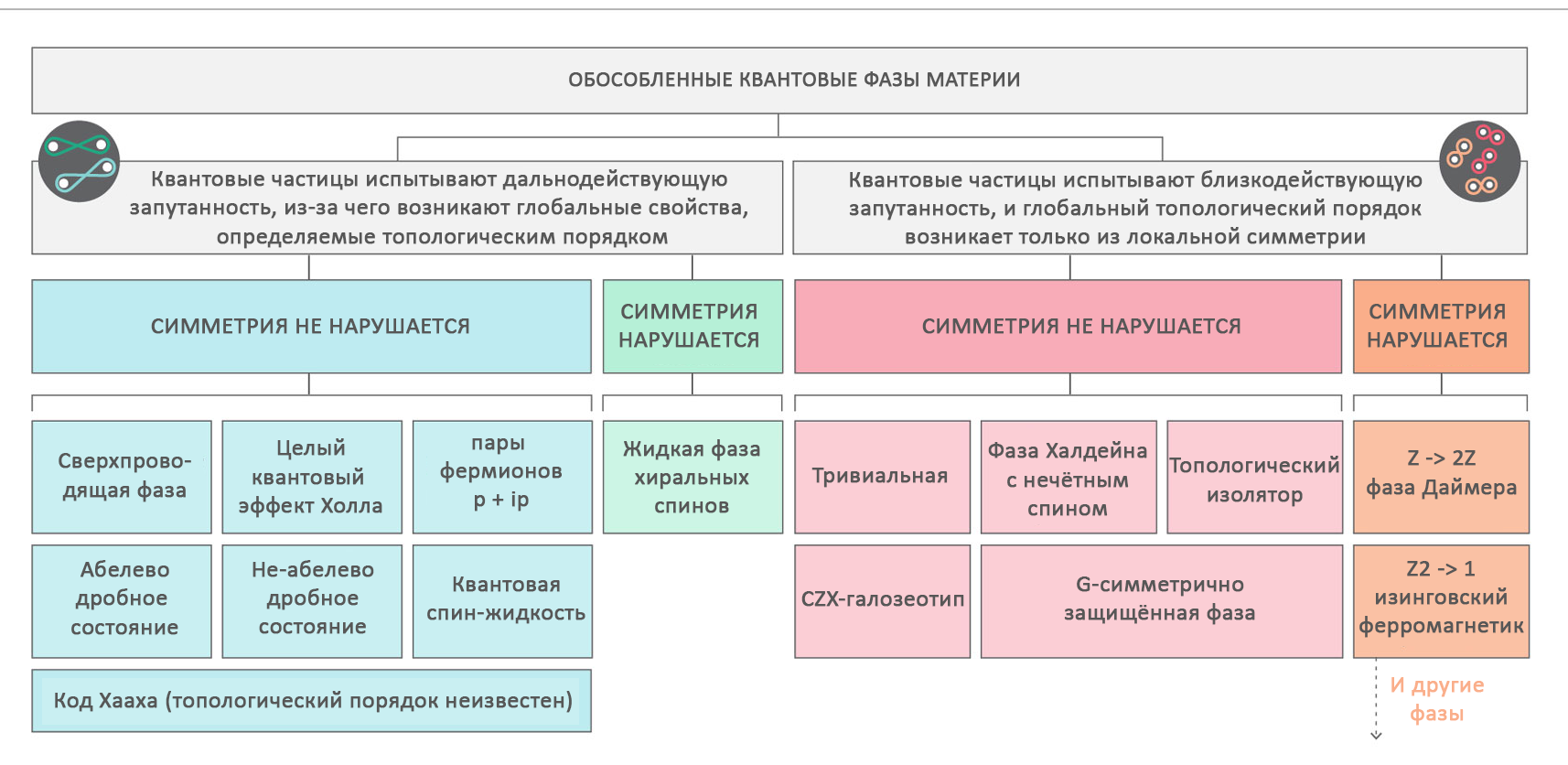Tableau périodique des phases: le tableau montre des exemples typiques de phases isolées, avec un état fondamental stable. La classification est considérée comme complète pour les espaces unidimensionnels et bidimensionnels. Pour les espaces tridimensionnels, on sait peu de choses.

Les phases bidimensionnelles sont beaucoup plus grandes et elles sont beaucoup plus intéressantes. Ils peuvent manifester ce que certains experts considèrent comme le «vrai» ordre topologique: l'ordre associé à l'intrication quantique à longue distance, comme les fluctuations de boucle dans un fluide de spin. Au cours des dernières années, les chercheurs ont montré que ces modèles d'enchevêtrement correspondent à des structures topologiques appelées catégories de tenseurs , numérotant de diverses manières les objets pouvant fusionner et s'enrouler les uns autour des autres. «Les catégories de tenseurs permettent de décrire les particules qui fusionnent et se tressent de manière cohérente», a déclaré David Perez-Garcia de l'Université Complutense de Madrid.

Des chercheurs, tels que Perez Garcia, travaillent sur la preuve mathématique que les classes bien connues de phases topologiques isolées bidimensionnelles sont complètes. Il a aidé à terminer les classes unidimensionnelles en 2010 , en utilisant la croyance généralement acceptée que ces phases sont toujours bien approximées par les théories quantiques des champs - des descriptions mathématiques dans lesquelles l'environnement où les particules quantiques existent est considéré comme lisse. "Ces catégories de tenseurs couvrent hypothétiquement toutes les phases bidimensionnelles, mais jusqu'à présent, il n'y a aucune preuve mathématique exacte", a déclaré Perez-Garcia. - Bien sûr, il serait beaucoup plus intéressant de prouver que ce ne sont pas toutes les phases. Les choses exotiques sont toujours plus intéressantes, car elles ont une nouvelle physique et elles peuvent être utiles. "

Les phases quantiques non isolées représentent un autre domaine de potentiel d'étude, mais sont enveloppées de brouillard qui est imperméable à la plupart des méthodes théoriques. «Nous ne pouvons pas parler le langage des particules et nous commençons à faire face à de très graves difficultés», explique Senthil Todadri , théoricien de la CS au MIT. Les phases non isolées, par exemple, constituent un obstacle majeur à la compréhension de la supraconductivité à haute température. Ils compliquent la vie des chercheurs sur la gravité quantique, qui ont rejoint le mouvement «tous les qubits», qui croient que non seulement les particules élémentaires, mais aussi l'espace-temps et la gravité apparaissent en raison des schémas d'enchevêtrement qui existent dans l'océan qubit sous-jacent. «Nous passons beaucoup de temps à travailler avec des États non isolés dans« tous les qubits »car c'est à partir de là que la gravité apparaît - du moins c'est ce que nous pensons en ce moment», a déclaré Brian Swingle , physicien théoricien à l'Université du Maryland. Certains chercheurs tentent d'utiliser le principe mathématique de la dualité pour transformer l'image d'une soupe quantique en une description équivalente de particules fabriquées dans une dimension supérieure. «Cela devrait être considéré comme une exploration de nouveaux territoires», explique Todadri.

L'enthousiasme encore plus grand des chercheurs est visible dans l'espace tridimensionnel. Jusqu'à présent, il est clair que lorsque les spins et les particules sont libérés des entraves de la bidimensionnalité et remplissent l'espace tridimensionnel de la réalité, des systèmes incroyablement étranges d'intrication quantique commencent à apparaître. «Jusqu'à présent, il y a des choses en trois dimensions qui échappent aux catégories de tenseurs», explique Perez-Garcia. "L'excitation [des champs] est complètement sauvage."

Code Haah

Et la plus folle des phases tridimensionnelles est apparue il y a sept ans.Un talentueux diplômé de Caltech, Jeongwan Haah, l'a découvert avec une simulation informatique lorsqu'il cherchait un «code de rêve»: un état quantique fondamental suffisamment fiable pour stocker en toute sécurité la mémoire quantique même à température ambiante.

Pour cela, Haah a dû se tourner vers trois dimensions. Dans les phases topologiques bidimensionnelles, comme un code toroïdal, une proportion importante d'erreurs est introduite par les «opérateurs de type chaîne»: des perturbations dans le système qui conduisent à la formation aléatoire de chaînes de spin. Ces chaînes peuvent parfois enrouler de nouvelles boucles autour du trou de tore, changeant le nombre de boucles de pair à impair et vice versa, convertissant le code toroïdal en l'un des trois autres états quantiques. Puisque les cordes se développent de manière incontrôlable et s'enroulent autour de tout le reste, les experts disent que dans un monde à deux dimensions, une bonne mémoire quantique ne peut pas être construite.


Jionwan Haah

Haach a écrit un algorithme de recherche de phase en trois phases qui évite les opérateurs de type chaîne. L'ordinateur a émis 17 solutions précises, qu'il a ensuite vérifiées manuellement. Il a été confirmé que les quatre phases sont exemptes d'opérateurs de type chaîne; l'une des phases présentant la plus grande symétrie est devenue le code Haach.

Le code de Haah est potentiellement utile pour stocker de la mémoire quantique, mais en même temps terriblement étrange. Xiao Chen, un théoricien de la FCC de Caltech, se souvient avoir entendu parler de cela en tant qu'étudiant diplômé en 2011, un mois ou deux après la découverte déroutante de Haah. «Tout le monde a été choqué», dit-elle. "Nous ne savions pas si nous pouvions faire quoi que ce soit." Et aujourd'hui, cette situation perdure depuis de nombreuses années. "

Le code Haach sur papier est assez simple: il s'agit d'une solution de l'équation énergétique à deux termes, décrivant des spins interagissant avec huit de ses plus proches voisins dans un réseau cubique. Mais la phase qui en résulte «met notre imagination à rude épreuve», a déclaré Todadri.

La caractéristique du code est des entités de type particules, des fractons, qui, contrairement aux modèles de boucles dans les liquides de spin quantiques, ne sont pas liquides et restent en place; les fractons ne peuvent sauter entre leurs positions dans le réseau que si ces positions sont traitées comme un motif fractal. C'est-à-dire, par exemple, pour forcer les fractons se tenant aux sommets du tétraèdre à échanger des places, il est nécessaire de verser de l'énergie dans chaque sommet du système; mais si vous augmentez l'échelle, il s'avère que ce que nous avons considéré comme le pic se révèle être en fait les quatre sommets du plus petit tétraèdre plus fin, et nous devons également verser de l'énergie dans tous ces sommets. Toujours en zoomant, on retrouve encore un tétraèdre encore plus petit, et ainsi de suite. Ce comportement fractal signifie que le code Haah n'oublie jamais la grille sous-jacente,et il ne peut pas être approximé par une description fluide du réseau, comme cela se fait dans la théorie quantique des champs. De plus, le nombre d'états fondamentaux du code Haach croît avec la taille du réseau situé à la base - et cette propriété n'est certainement pas topologique (si vous étirez un tore, il reste toujours un tore).

L'état quantique du code Haach est extrêmement stable, car il est peu probable qu'un opérateur fractal idéal pour lui apparaisse au hasard. Les experts disent que la version implémentée de ce code peut être d'un grand intérêt d'un point de vue technologique.

La phase Haah a déclenché une vague de raisonnement théorique. Haah a aidé à cela lorsque, en 2015, avec deux collègues du MIT, il a découvert de nombreux exemples dans la classe de phase, maintenant connue sous le nom de «modèles de fracton», des parents simplifiés du code Haach. Le premier modèle de cette famille a été présenté par Claudio Chamon de l'Université de Boston en 2005. Chen et d'autres scientifiques ont étudié la topologie des systèmes de fractons, dont certains permettent aux particules de se déplacer le long de lignes ou d'avions dans un espace tridimensionnel, ce qui leur permet de mieux comprendre ce qui se passe ou peuvent être plus adaptés à une mise en œuvre expérimentale. «Cela ouvre la voie à de nombreuses autres choses exotiques», dit Chen à propos du code Haah. - Ceci est une démonstration du peu que nous savons sur le monde tridimensionnel et les dimensions supérieures.Et comme nous n'avons pas encore une image systématique de ce qui se passe, nous attendons beaucoup de découvertes de toutes sortes. "

Jusqu'à présent, personne ne sait à quelle partie du paysage des phases possibles appartient le code Haach et ses proches, ni la taille de l'espace des possibilités. Selon Todadri, la communauté a progressé dans la classification des phases tridimensionnelles isolées les plus simples, mais davantage de recherches sont nécessaires avant le début du programme de classification complet. Selon lui, il est clair que "lorsque nous classerons les phases isolées de la matière dans un espace tridimensionnel, nous devrons faire face à de telles possibilités étranges, dont l'une a été découverte pour la première fois par Haah".

De nombreux chercheurs pensent que de nouveaux concepts de classification peuvent être nécessaires pour décrire la nature fractale du code Haah et pour découvrir le spectre complet des possibilités de la matière quantique tridimensionnelle. Ven a déclaré: "Nous avons besoin d'un nouveau type de théorie, d'une nouvelle façon de penser." Peut-être, a-t-il dit, nous avons besoin d'une nouvelle image des schémas non fluides d'implication à long terme. «Nous avons quelques idées générales, mais il n'y a pas de mathématiques systématiques pour leur mise en œuvre», a-t-il déclaré. - Nous avons une certaine impression de son apparence. Une systématisation détaillée ne suffit pas. Mais c'est excitant. "