Passage de Vénus sur le disque du Soleil et détermination de la distance entre eux

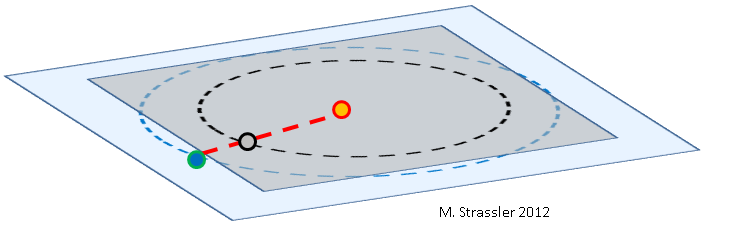
Fig. 1: la Terre (bleu), Vénus (gris) et le Soleil (orange), pas à l'échelle.

Concernant le passage de Vénus à travers le disque du Soleil en 2012, de nombreux articles ont déjà été écrits. À propos de la rareté de cet événement, et pourquoi exactement: en théorie, Vénus, se déplaçant autour du Soleil plus souvent que la Terre, devrait passer entre la Terre et le Soleil à chacun de ses tours (Fig.1), mais parce que les orbites de deux planètes ne sont pas alignées (elles ne sont pas dans le même plan, voir Fig.2), Vénus passe souvent au-dessus ou en dessous du Soleil du point de vue de la Terre.

Mais au lieu de répéter les mots des autres, je veux ajouter quelques détails qui ne sont pas si faciles à trouver sur Internet.

Vous avez peut-être lu qu'en utilisant une technique basée sur le raisonnement de l'astronome Edmund Halley (la célèbre comète Halley) faite par lui de 1678 à 1716, ainsi que de James Gregory pour lui, le passage de Vénus en 1716 a été utilisé pour déterminer la distance de la Terre à Le Soleil (et avant Vénus, et toutes les autres planètes) avec une erreur de 2% est le plus élevé de ceux atteints à cette époque. On espérait que la précision serait 10 fois plus élevée, mais un effet optique inattendu appelé « effet de goutte noire » est intervenu dans le processus - il y a encore des débats sur les raisons exactes de son apparition. Mais vous n'avez peut-être pas lu que cette mesure - et de nombreuses autres mesures des distances en astronomie, jusqu'à des étoiles assez proches - est basée sur le principe de la parallaxe , sur le même fait géométrique que nos yeux et notre cerveau utilisent pour percevoir la profondeur, ou notre capacité à ressentir à quelle distance les objets sont loin de nous simplement en les regardant.


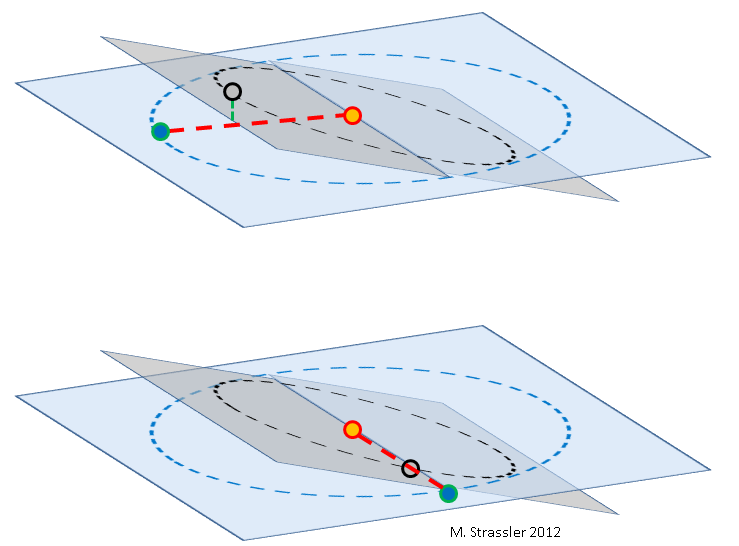Fig. 2: Terre (bleu), Vénus (gris) et Soleil (orange), pas à l'échelle. L'orbite de Vénus (un cercle noir dans un rectangle gris) est inclinée par rapport à l'orbite de la Terre (un cercle bleu dans un rectangle bleu). Le degré d'inclinaison est fortement exagéré. Puisque la Terre et Vénus tournent autour du Soleil à des vitesses différentes, elles peuvent se croiser à tout moment sur les orbites.

En haut: lors de ce passage, Vénus se situe au dessus ou en dessous (ligne verte) de la ligne reliant la Terre et le Soleil (ligne rouge), donc Vénus ne passe pas à travers le disque solaire.

Ci-dessous: Dans de rares cas, la ligne reliant la Terre et le Soleil coïncide avec la ligne d'intersection des plans des orbites, et Vénus est proche de la même ligne, ce qui conduit au passage.

Sans parallaxe, il est également facile de déterminer la distance relative de Vénus au Soleil, c'est-à-dire le rapport du rayon de l'orbite de Vénus L _V au rayon de l'orbite terrestre L _E. Par conséquent, en astronomie de la Renaissance, les distances relatives des planètes à la Terre et au Soleil ont été calculées assez tôt. Mais pour déterminer séparément L _V et L _E , il est nécessaire de mesurer la parallaxe, et le passage de Vénus peut la fournir. Le passage de Vénus dans les années 1760 a donné une mesure assez précise de L _E - L _V , la distance «absolue» de la Terre à Vénus; cela a permis de découvrir L _E , L _V et les distances à toutes les autres planètes avec une erreur de quelques pour cent. Avant cela, à la fin du XVIIe siècle, une mesure de la distance de la Terre à Mars avait une erreur d'environ 10%; il était également basé sur la parallaxe, mais c'est une histoire complètement différente.

Remarque préliminaire: la Terre et Vénus, et même le Soleil sont très petits par rapport aux distances entre eux, il est donc presque impossible de dessiner des images précises. Dans les illustrations, vous devez toujours dessiner des planètes plus grandes qu'elles ne le sont réellement, par rapport aux distances entre elles, juste pour que vous puissiez comprendre le concept. Gardez cela à l'esprit! Toutes mes illustrations ne sont pas dessinées à l'échelle.

Les tailles relatives des orbites de Vénus et de la Terre

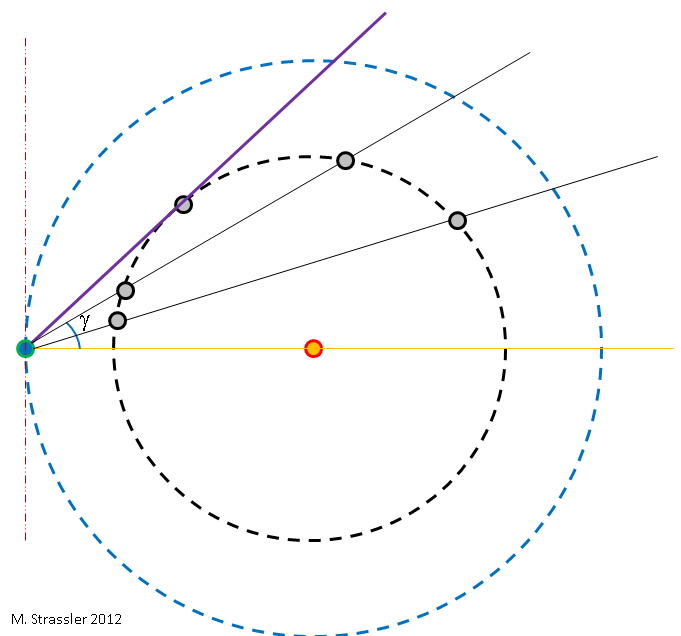Fig. 3

Pour comprendre la raison principale de la simplicité de la détermination de L _V / L _E , supposons que les orbites de la Terre et de Vénus soient circulaires et alignées - elles se trouvent dans le même plan (comme le montre la figure 1, isométrique, et la figure 3 est une «vue de dessus»). En fait, les orbites de la Terre et de Vénus sont légèrement allongées et non alignées (Fig.2). Mais l'ellipticité et l'inadéquation des avions ne sont pas très importantes pour notre raisonnement, nous pouvons donc d'abord les ignorer, puis nous souvenir à nouveau pour obtenir des réponses plus précises.

Ici, nous appliquerons la technologie classique pour la physique: nous ferons une approximation suffisante pour la tâche actuelle et nous n'irons pas plus loin que nécessaire. C'est une façon très puissante de penser la science et les connaissances en général - il suffit de répondre à toute question avec un certain niveau de précision, afin que vous puissiez utiliser la technique la plus simple parmi celles qui vous donneront le niveau de précision souhaité. Cette méthode est parfaitement utilisée depuis des siècles et ne s'applique pas seulement à la physique.

Par conséquent, nous prendrons l'approximation dans laquelle les orbites sont circulaires et alignées, et nous recevrons approximativement les bonnes réponses, avec une erreur de quelques pour cent. Ce sera suffisant pour démontrer les concepts de base que je recherche. Croyez-moi, vous pouvez faire des calculs beaucoup plus précis - ou vous pouvez devenir vous-même un expert en la matière. Mais notre approximation donnera non seulement une très bonne réponse, mais elle pourra également montrer pourquoi il est si facile de calculer le rapport de L _V à L _E , mais pas les valeurs de L _V et L _E elles-mêmes.

Au cours de l'année où la Terre et Vénus tournent autour du Soleil à différentes vitesses, la position relative de la Terre et de Vénus par rapport au Soleil change. Si un certain jour (jour, mois, année) je décide de dessiner une image avec le Soleil au centre et avec la Terre à gauche, comme dans la Fig. 2, alors Vénus peut être n'importe où sur son orbite. Cela signifie que du point de vue de la Terre, l'angle entre Vénus et le Soleil dans le ciel changera en fonction de la date. Ceci est illustré sur la fig. 3, où l'angle est appelé γ. L'angle est facile à mesurer; trouver Vénus dans le ciel après le coucher du soleil ou avant le lever du soleil et mesurer l'angle entre Vénus et le Soleil; voir la photo 4.


Fig. 4

De la fig. La figure 3 montre que γ a une taille maximale - l'angle entre les lignes orange et violette. Se déplaçant en orbite, Vénus apparaîtra ailleurs à chaque coucher de soleil; pendant un certain temps, il s'élèvera plus haut au-dessus de l'horizon pendant plusieurs nuits d'affilée, puis commencera progressivement à apparaître en dessous. En observant Vénus pendant plusieurs nuits d'affilée et en mesurant γ, nous pouvons déterminer la valeur maximale de γ, que j'appellerai γ _max .

De la fig. 3, il est évident que (comme le montre la figure 4) γ _{max est} inférieur à 90 °, car la ligne violette doit se situer entre l'orange et le rouge, perpendiculaire. Géométriquement, c'est une conséquence du fait que Vénus est toujours plus proche du Soleil que de la Terre. Ces angles expliquent pourquoi Vénus est toujours visible immédiatement après le coucher du soleil ou avant l'aube (sauf pour les jours où elle est située derrière le Soleil). Vénus ne peut pas être à son zénith après la tombée de la nuit, car pour cela, elle devrait être à gauche de la ligne rouge.


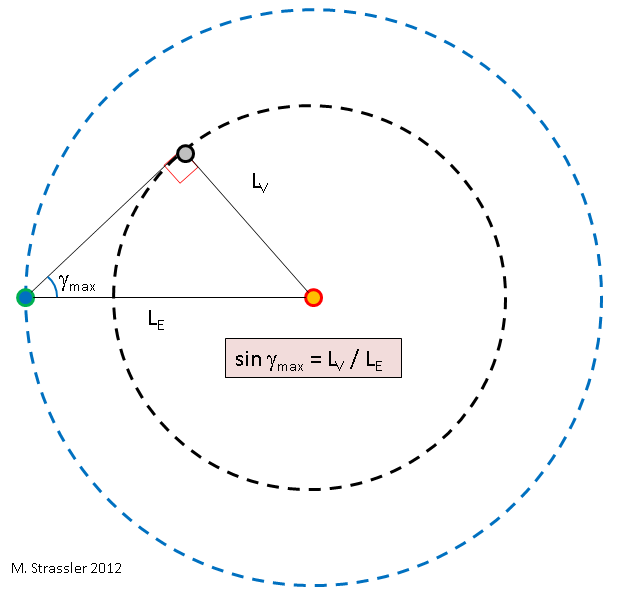Fig. 5

Nous pouvons maintenant déterminer le rapport des rayons de deux orbites - L _V à L _E - en utilisant γ _max . Il s'agit de la géométrie la plus simple, voir fig. 5. L'essentiel est que lorsque Vénus est à l'angle maximum du Soleil, la ligne entre le Soleil et Vénus est perpendiculaire à la ligne entre la Terre et Vénus, de sorte que les lignes reliant ces trois objets forment un triangle rectangle. À partir de là, nous utilisons la trigonométrie standard:

$$

$$L_V / L_E = \ gamma_ {max}$$

Et à partir d'ici, à l'aide d'autres formules géométriques simples, nous obtenons la relation entre les distances aux autres planètes.

Ce n'est pas tout à fait exact, pour les raisons indiquées au début; les orbites des planètes sont des ellipses et ne se trouvent pas sur le plan d'eau. En d'autres termes, L _V et L _E ne _sont pas stockés au cours de l'année, et γ _max est appliqué un peu plus compliqué, en trois dimensions, comme sur la Fig. 2, mais pas en deux, comme sur la Fig. 1, 3 et 5. Mais à l'aide de mesures précises de la position de Vénus et du Soleil dans le ciel, il est possible de déterminer les orbites exactes de Vénus et de la Terre autour du Soleil et d'améliorer les calculs. Le sens est le même; toutes les mesures de la position de Vénus et du Soleil dans le ciel nous permettent seulement de mesurer les tailles relatives des orbites de Vénus et de la Terre. Mais les valeurs exactes de L _V et L _E ne peuvent pas être déterminées de cette façon. Ici, nous avons besoin d'une approche différente.

Passage de Vénus, parallaxe et distance au Soleil

La raison pour laquelle le passage de Vénus vous permet de mesurer les valeurs absolues des orbites de la Terre et de Vénus est que ce processus peut être observé avec une grande précision à différents endroits du globe, à la suite de quoi vous aurez deux perspectives de l'emplacement visible de Vénus par rapport au Soleil, mesurées à partir de différents endroits avec des distance entre eux. Mesurer la parallaxe vous permet de déterminer la valeur absolue de la distance de la Terre à Vénus à partir de l'angle de parallaxe et la distance entre deux points de mesure sur Terre - tout comme un type d'objet différent pour les yeux gauche et droit permet à notre cerveau de nous donner une impression de profondeur - une impression de distance par rapport aux objets.


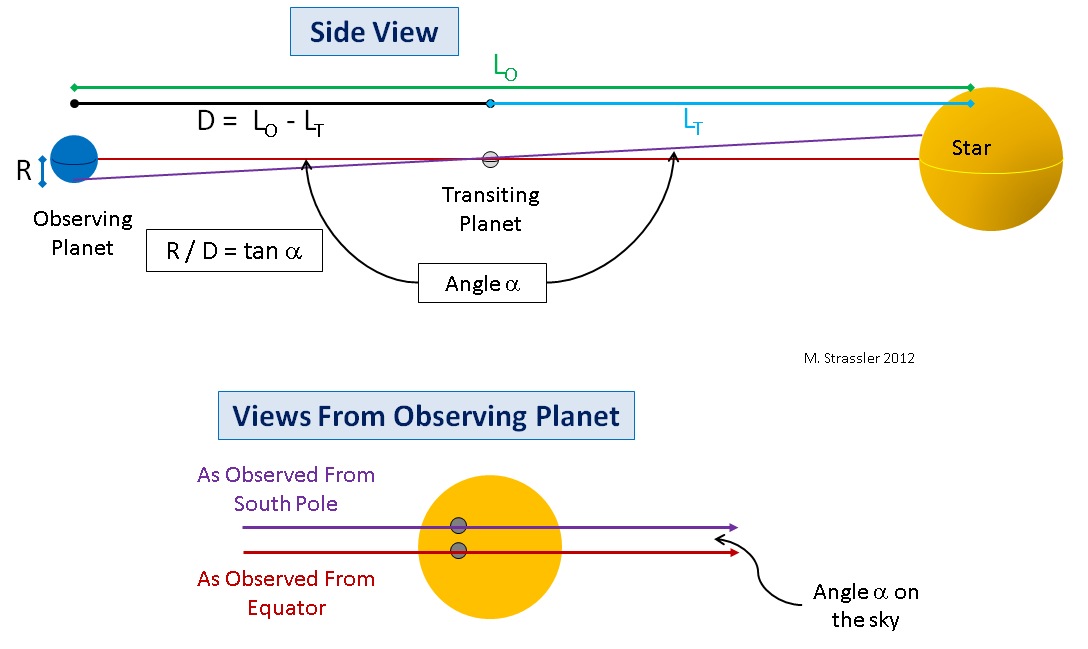Fig. 6

Pour une démonstration, permettez-moi de dessiner à quoi cela ressemblera sur une grande planète. Dans la fig. La figure 6 montre la planète avec laquelle nous observerons le passage (ce sera la Terre) et la planète passant devant l'étoile (ce sera Vénus). Je présenterai une situation simplifiée (juste pour rendre la géométrie plus simple et le concept principal plus facile à voir), dans laquelle les planètes et l'étoile sont alignées, donc du point de vue de l'observateur à l'équateur, une planète passant passera le long de l'équateur de l'étoile. Ci-dessus sur la fig. 6 montre une vue latérale; notez la ligne rouge de l'équateur de la planète observatrice à l'étoile en passant par l'équateur de la planète passant par le disque de l'étoile.

Dans le cas d'un alignement parfait, l'observateur à l'équateur de la planète extérieure verra comment la planète intérieure passe le long de l'équateur de l'étoile. Ceci est représenté par une ligne rouge au bas de la fig. 6. Mais l'observateur du pôle sud de la planète extérieure verra comment la planète intérieure passe l'étoile le long du chemin (ligne violette) au nord de l'équateur de l'étoile (dans le cas du pôle nord, tout sera vice versa). Si nous mesurons l'angle α dans le ciel entre les chemins le long desquels une planète passant se déplace et connaissons le rayon R de la planète observatrice, nous pouvons dessiner un triangle rectangle reliant la planète passant, le centre de la planète observatrice et le pôle de la planète observatrice, avec un petit angle? La trigonométrie simple nous donnera la distance D entre les planètes pendant le passage, où

$$

$$D = R / tan \; \ alpha$$

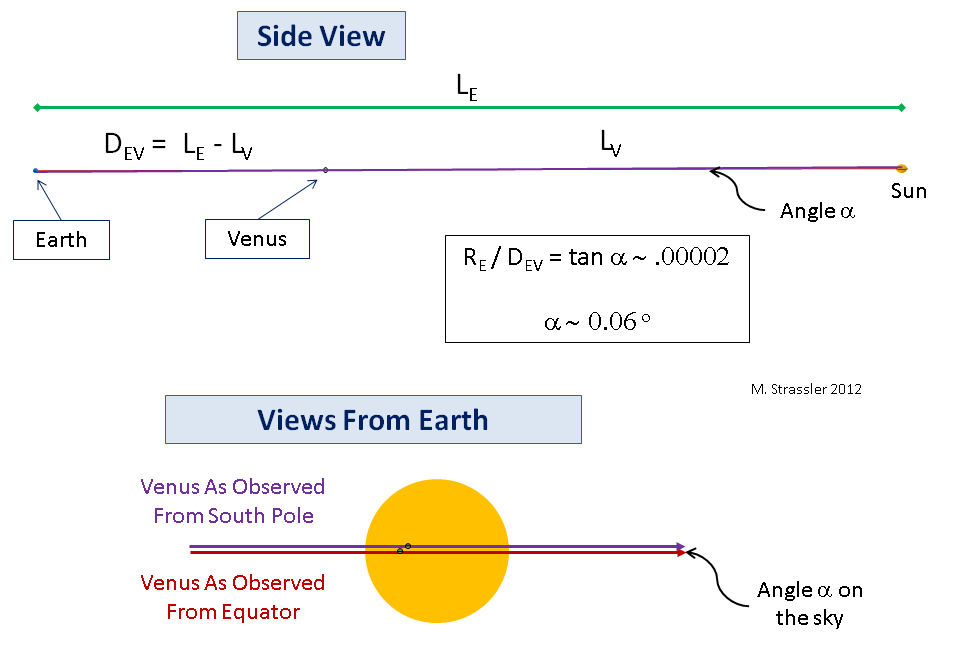Fig. 7

Il en va de même pour la Terre, Vénus et le Soleil, sauf que la Terre et Vénus sont si petites par rapport à la distance entre elles et le Soleil que l'angle α sera égal à environ 1/20 °! (Il s'agit d'une quantité assez petite, mais tout à fait mesurable, bien qu'une mesure exacte de la distance au Soleil, que les astronomes du 18e siècle voulaient obtenir, nécessiterait une mesure techniquement précise et assez compliquée de la magnitude d'un petit angle). Je ne dessinerai pas un si petit angle, vous devez donc me croire sur parole que ce qui se passe est une version de ce que j'ai représenté sur la fig. 6, avec des planètes et une étoile (le Soleil) beaucoup plus petites que celles qui y sont peintes, par rapport aux distances. Même l'image de la fig. 7 rend les planètes beaucoup plus grandes qu'elles ne le sont. Mais l'idée reste inchangée: la distance D _EV entre la Terre et Vénus lors du passage peut être déterminée en mesurant l'angle de parallaxe α (bas de la Fig.7; notez que le diamètre angulaire du Soleil est d'environ 1/2 °).

Cependant, de nombreuses questions subsistent:

• J'ai dit comment mesurer D _EV , la distance de la Terre à Vénus pendant le passage. Mais notre objectif n'était-il pas de mesurer L _E et L _V , la distance de la Terre au Soleil et de Vénus au Soleil?
• Personne ne s'est rendu au pôle sud de la Terre pour observer le passage de Vénus en 1761 ou 1769.
• J'ai supposé des orbites parfaitement alignées de la Terre, de Vénus et de la position du Soleil, de sorte qu'à partir d'un point sur l'équateur de la Terre, on pouvait voir Vénus se déplacer le long de l'équateur du Soleil. Mais ce n'est en fait pas le cas, et cela ne ressemble même pas à une procédure pas à pas typique (et en 2012, ce n'était pas le cas non plus).
• L'angle α est suffisamment petit pour être mesuré avec précision - en particulier dans les jours précédant la photographie et la messagerie instantanée, en l'absence d'indications claires de l'emplacement du pôle nord du Soleil, ce qui rend difficile de comparer avec précision les mesures du chemin de Vénus faites à partir de deux points différents sur la Terre. Cependant, l'objectif principal était de mesurer l'angle pas moins de 1 partie sur 500 (0,2%) (bien qu'en raison de l'effet de goutte noire, le résultat était plus proche de 1 partie sur 50 (2%)).

Comment faire face à ces problèmes?

Tout d'abord, comment passez-vous de la mesure de D _EV à la mesure des valeurs souhaitées, L _E et L _V ? C'est simple - nous connaissons déjà toutes les relations, en particulier, nous connaissons déjà L _E / L _V (approximativement, à partir de la figure 4, ou, si nous abordons la question plus attentivement, nous pouvons calculer et plus précisément) à partir de l'angle maximum γ _max entre Vénus et Le soleil du point de vue de la Terre. Nous connaissons également D _EV = L _E - L _V = L _E (1 - L _V / L _E ) de la Fig. 7. Par conséquent, nous pouvons obtenir une valeur approximative de L _{E en} utilisant:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - sin \; \ gamma_ {max})$$

où α est l'angle de parallaxe mesuré pendant le transit et γ _max est l'angle maximum entre Vénus et le Soleil (Fig. 5). Des mesures plus précises nécessitent une géométrie plus complexe, mais avec la même idée de base.

Deuxièmement, même si les orbites des planètes étaient parfaitement alignées, il n'est pas nécessaire de mesurer deux dimensions de la trajectoire de Vénus à partir de l'équateur et du pôle de la Terre. Ils peuvent être mesurés sous deux latitudes quelconques. La géométrie devient un peu plus compliquée, mais pas beaucoup, mais le principe demeure (voir Fig. 8).


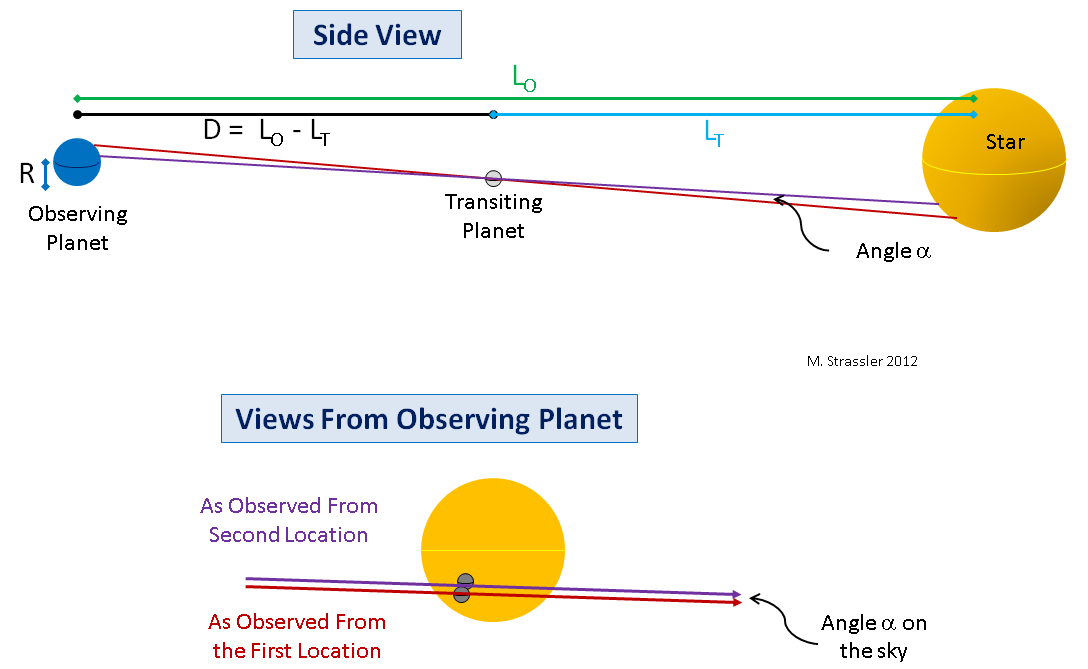Fig. 8

Troisièmement, même sans alignement parfait, un petit angle de parallaxe apparaît lors de la mesure de valeurs à partir de deux points différents de la Terre, et si cet angle est bien mesuré, cette mesure peut être transformée (via des équations légèrement plus complexes) en une mesure D.Ceci est illustré sur la Fig. 8, vers le bas.

La quatrième question est le problème historiquement complexe de mesurer le décalage angulaire du chemin de Vénus en passant par l'angle α nous amène à une autre tentative de mesurer le temps - soit le temps de voyage, soit simplement le début et la fin du passage, et non les angles. La première option a été proposée par Halley sur la base des idées de Gregory, et la seconde, en tant qu'amélioration supplémentaire, a été proposée par Joseph Nicola Delille . La méthode Halley ne nécessitait pas de synchronisation d'horloge à différents endroits de la Terre; La méthode de Delil requise était donc basée sur une technologie horlogère plus avancée.

Même au XVII ou XVIII siècle, il est beaucoup plus facile de mesurer avec précision l'intervalle, ou les moments du début et de la fin d'une éclipse, que de mesurer avec précision l'emplacement de Vénus par rapport au disque du Soleil, surtout en l'absence de photographie. Dans la fig. La figure 9 montre que les trajectoires violette et rouge de Vénus traversant le Soleil ont des longueurs légèrement différentes car elles ne le traversent pas en un seul endroit, ce qui signifie que la durée du passage différera selon le temps associé à l'angle de parallaxe. Malheureusement, tout se révèle plus compliqué qu'il n'y paraît à première vue - la Terre tourne et se déplace autour du Soleil, de sorte que l'observateur parcourt une distance assez considérable lors du passage de Vénus à travers le disque du Soleil. Par conséquent, beaucoup d'efforts sont nécessaires (les calculs sont assez compliqués, bien qu'avec les ordinateurs modernes, ils soient beaucoup plus simples) pour déterminer la différence d'intervalles de temps du début et de la fin du passage observée par deux observateurs différents sur Terre, en fonction de la distance au Soleil.

Halley au début du XVIIIe siècle a compris tous les principes géométriques nécessaires (si vous soustrayez la phraséologie et le style anglais obsolètes de ses textes, vous serez surpris de la façon dont ses déclarations complexes sonnent moderne, et vous verrez que les scientifiques d'il y a trois cents ans étaient très similaires aux scientifiques d'aujourd'hui, possédait la même intelligence et ne manquait que de la technologie scientifique d'aujourd'hui).


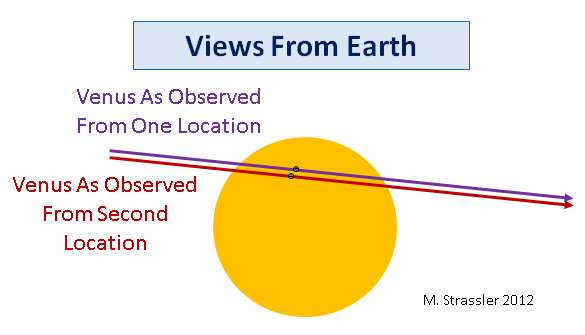Fig. 9

Tout cela suggère que la parallaxe - la différence de position visible attribuée à Vénus par rapport au Soleil du point de vue des observateurs le mesurant en même temps mais à partir de différents endroits sur Terre - a historiquement été une méthode très importante par laquelle déterminé la taille du système solaire. Aujourd'hui, des méthodes plus puissantes sont à notre disposition, mais vous pouvez être intéressé par le fait que ce que vous voyez aujourd'hui dans le ciel est d'une grande importance historique, ou vous pouvez simplement profiter de la vue de Vénus, se déplaçant majestueusement autour de notre étoile.