
Vous êtes donc programmeur. Pourquoi avez-vous même besoin de polynômes? Par exemple, alors, que c'est une bonne argile géométrique, à partir de laquelle vous pouvez modeler différentes choses.
À partir de notre
article expliquant l'essence de l'analyse mathématique en utilisant le python, le sang et la dynamite comme exemple, on peut voir que vous pouvez analyser et synthétiser des fonctions arbitraires en tant que polynômes. Cependant, il n'est pas nécessaire de travailler spécifiquement avec des fonctions. Parfois, vous devrez peut-être modéliser une spline à partir de plusieurs points ou propriétés, tels que les tangentes des courbes. Par exemple, vous devez créer une sorte d'animation, ou un bel effet vidéo, ou dessiner une courbe passant par certains points, ou créer une surface qui est plate à un endroit et incurvée à un autre.
Les polynômes, y compris les splines, ne sont pas toujours le meilleur outil pour cette tâche, mais ils possèdent certaines fonctionnalités que les programmeurs apprécient vraiment. Ils sont simples et polyvalents et, surtout, très efficaces en termes de performances. Prenons par exemple le polynôme suivant:
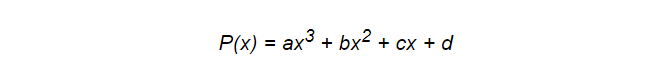
Pour le calculer, seules 6 actions de multiplication et 3 ajouts sont nécessaires. Ceci est important car votre modèle sera constamment soumis au calcul. Mais ici, nous pouvons effectuer une optimisation. Le plan de Horner nous aidera à cela. Avec son aide, le même polynôme peut s'écrire

Et ce n'est que 3 multiplications et 3 additions. Vous voyez, nous venons de commencer et vous avez déjà appris à vous débarrasser d'un tiers des calculs.
Interpolation polynomiale
L'adaptation d'un polynôme de degré
n à
n + 1 points dans l'espace est appelée interpolation polynomiale. Il existe plusieurs façons de le mettre en œuvre. Vous pouvez utiliser les formules d'interpolation de
Newton ou
Lagrange , mais le moyen le plus simple d'obtenir le polynôme d'interpolation est de résoudre un système d'équations linéaires.
Si un polynôme passe par un point, alors on peut évidemment dire que
P (xi) = yi . Supposons que nous voulions adapter un polynôme à un ensemble de trois points. Cela signifie que:

Dans le cas général, nous ne pouvons pas tracer une ligne passant par trois points arbitraires. Et donc nous devons le plier, formant une parabole. Ou, en d'autres termes, introduire un polynôme du deuxième degré, également connu sous le nom de fonction quadratique.

Puisque xs et ys sont connus, il suffit de résoudre le système et de trouver les coefficients a, b, c, et comme ce système se compose de trois équations et de trois variables, nous pouvons généralement obtenir une seule solution.
Pour vous en assurer, essayez de déplacer la position des trois points dans le graphique inférieur et voyez ce qui se passe.

Ce graphique est également très utile pour l'analyse mentale des systèmes linéaires. Dans le cas général, il est impossible d'ajuster une droite en trois points, tout comme il est impossible de trouver une solution pour un système de n équations avec n-1 variables inconnues. Mais parfois c'est possible. Par exemple, dans le cas où certains des points coïncident ou tous sont intentionnellement situés sur une seule ligne droite.
La situation inverse est encore plus intéressante. Nous pouvons dessiner un nombre infini de paraboles à travers deux points donnés. Tous conviennent également comme solution au problème. Et en même temps, nous ne pouvons pas obtenir une meilleure solution unique pour les systèmes de n équations et n + 1 variables.
Et si c'était encore possible? Et si nous pouvions introduire un critère supplémentaire pour choisir l'option la plus appropriée?
La synthèse
Des questions similaires nous conduisent au territoire de la synthèse polynomiale. Dans notre cas, il s'agit d'un croisement entre séries polynomiales et interpolation polynomiale. À l'aide de séries, nous pouvons modéliser une fonction basée sur ses dérivées à un moment donné, et à l'aide de la synthèse, nous pouvons utiliser à la fois des points et des dérivés (et pas seulement eux, mais plus encore une autre fois).
La dérivée d'une fonction est étroitement liée aux propriétés géométriques de son graphique. La première dérivée détermine la tangente de la pente de la tangente et la seconde détermine la courbure.
Supposons que nous ayons besoin de définir une fonction passant par deux points, connaissant sa tangente aux deux points. Dans ce cas, nous pouvons facilement le synthétiser comme un polynôme.
Comme précédemment, nous devons noter un système d'équations. Maintenant, nous avons besoin de quatre conditions, nous devons donc choisir un polynôme de degré 3, c'est-à-dire une fonction cubique.
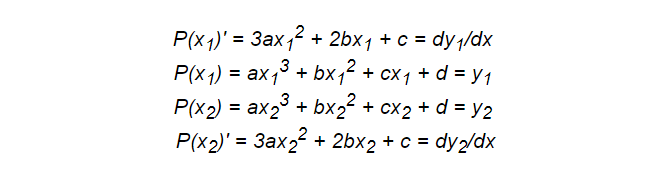
Certaines équations sont basées sur des points, tandis que d'autres sont des dérivés. Des intégrales peuvent également être ajoutées ici pour introduire les propriétés entières nécessaires, ce qui rend cette technique assez efficace.
Mais nous continuerons à considérer une fonction reliant deux points d'une droite continue avec des contraintes tangentielles en ces points.


Phénomène de runge
L'interpolation polynomiale a une propriété désagréable, qui se manifeste par une augmentation de la croissance des oscillations aux deux extrémités de l'intervalle avec une augmentation du nombre de points. Ce phénomène est appelé le phénomène Runge. Il limite la possibilité d'utiliser des interpolations polynomiales simples.
Un autre inconvénient de cette approche est sa nature globale, c'est-à-dire un changement dans la fonction entière avec le moindre changement dans la position d'au moins un point. En combinaison avec des oscillations, le résultat même est le chaos.

Noeuds de Chebyshev
L'une des façons de lutter contre le chaos est de sélectionner un maillage spécial pour l'interpolation -
les nœuds Chebyshev . Ce sont des valeurs x spéciales qui sont obtenues en divisant un demi-cercle avec un rayon de 1 en fragments égaux et en les projetant sur l'axe x.
En général, une certaine magie mathématique est cachée dans cette technique, mais d'un point de vue pragmatique, elle vise à minimiser le phénomène de Runge. Et même si cela ne permet pas de rendre l'interpolation complètement prévisible, tout fonctionne de manière stable sur l'intervalle (-1: 1).

Bien sûr, vous pouvez étendre l'intervalle le long de l'axe X autant que vous le souhaitez en utilisant la transformation affine unidimensionnelle. Il n'est pas nécessaire d'adhérer au segment
(-1; 1) .
Mais l'interpolation conserve en même temps son omniprésence. La modification du premier point affecte toujours le fonctionnement de la fonction près du dernier, mais pas de manière significative.
Splines
Il existe plusieurs variétés de splines, mais toutes sont unies par un scénario d'application. Dès que l'interpolation globale pour une raison quelconque cesse de convenir à nos tâches, nous pouvons diviser notre intervalle en fragments plus petits et définir des fonctions individuelles pour l'interpolation sur chacun d'eux.
La seule chose que nous devons considérer est la nécessité de les connecter aux extrémités pour maintenir la continuité. Si nous garantissons la continuité non seulement de la fonction finale, définie par morceaux, mais aussi de sa dérivée première, alors dans ce cas, les tangentes de chacun de ses segments coïncideront et son calendrier sera lisse.
Il existe une certaine
classification des splines. Par exemple, prenez une spline polynomiale composée de deux fragments. Si chaque fragment de celui-ci est déterminé par un polynôme du troisième degré, alors il est appelé cubique. Elle peut posséder, par exemple, une propriété telle que la continuité de la première dérivée, car les tangentes à la jonction des fragments coïncident. Ses fragments ne sont pas de largeur égale. Il n'est pas d'origine naturelle, car nous pouvons contrôler les dérivés à ses extrémités. Et bien sûr, il s'agit d'une spline d'interpolation, car elle passe exactement à travers les points de grille que nous avons indiqués.

Conclusion
La probabilité que vous ayez à mettre en pratique votre propre interpolation est extrêmement faible. Il existe de nombreuses solutions toutes faites et dans la plupart des cas, vous n'aurez qu'à choisir le bon outil pour le travail. Ce domaine de connaissance n'est pas si compliqué, mais le nombre de mots et de noms inconnus peut repousser.
Le but de ce guide était de vous fournir une compréhension de base des idées utilisées pour travailler avec des polynômes et des splines. En aucun cas il ne prétend être complet, car en fait, des livres entiers sont écrits sur chacun des petits chapitres de ce matériel. Mais nous espérons, au moins, que l'approche interactive de la présentation dans ce document sera utile non seulement pour une brève introduction, mais si un tel besoin se présente, il vous aidera à maîtriser des sujets plus avancés.
