Cosmologie - Stanford. Abstrait. Conférence 1

Cet article ouvre une série de notes de cours sur la cosmologie de l'Université de Stanford. Les conférences elles-mêmes en anglais sont disponibles à: Cosmology (2013) - Leonard Susskind - Stanford University . J'ai regardé la conférence vidéo et décrit avec plaisir. Le conférencier Leonard Susskind explique très accessible et amusant. Il est évident qu'il est une personne talentueuse et un excellent professeur.

L'université de Stanford est également célèbre pour le fait que notre remarquable compatriote Andrei Linde y travaille, qui recevra probablement bientôt le prix Nobel de physique pour sa contribution à la cosmologie moderne. Peu importe, je vous conseille de regarder sa conférence publique Les nombreux visages de l'univers .

Ce synopsis est ma tentative d'auto-éducation. Je l'écrirais toujours pour moi-même dans un cahier. Mais j'ai décidé de combiner affaires et plaisir. J'espère que ce sera intéressant pour quelqu'un aussi.

Faites immédiatement une réservation que j'ai essayé de prendre des notes proches du texte original. Cependant, dans certains endroits, je me suis permis de compléter ou de généraliser les déclarations du professeur en fonction de ma propre expérience en tant que physicien spécialisé. Cela a été fait uniquement dans le but de faciliter la compréhension, la compréhension et l'assimilation du matériel.

Dans cet article, un synopsis de la leçon 1 est proposé à votre attention. Peut-être une suite apparaîtra plus tard.

Revue historique

La cosmologie est un sujet très ancien. L'histoire de la cosmologie remonte à des milliers d'années. En particulier, les anciens Grecs connaissaient la cosmologie depuis très longtemps.

Ces conférences couvrent la période ne dépassant pas la seconde moitié du XXe siècle, quand Edwin Hubble a découvert la loi de l'expansion de l'univers.

Si nous parlons de la cosmologie en tant que science, il s'agit d'un domaine de connaissances assez nouveau. La cosmologie moderne remonte à la découverte du rayonnement relique micro - ondes et à la formulation de la théorie du big bang . Et cela ne s'est produit que dans les années 1960.

Jusqu'à présent, la cosmologie n'était pas une branche de la physique, mais appartenait plutôt aux sciences naturelles. C'est-à-dire qu'en cosmologie l'approche phénoménologique a prévalu: observation, mesure, classification, catalogage, etc.

À cette époque, la précision des mesures était faible. Et donc il était impossible de formuler des déclarations exactes. Il y avait des équations, mais elles étaient incorrectes et inexactes. Les physiciens ont toujours été impliqués dans le processus d'étude, car les étoiles, les galaxies et autres corps célestes possèdent des caractéristiques physiques telles que le moment angulaire, par exemple. Les chimistes physiques étaient également impliqués, car les corps célestes ont une composition chimique.

Cependant, l'attitude envers l'Univers lui-même en tant qu'objet physique, l'Univers en tant que système qui devrait être étudié mathématiquement en utilisant un ensemble de principes physiques et les équations exactes correspondantes correspondantes - il s'agit d'une approche relativement jeune.

Propriétés de l'univers

Dans ces conférences, l'Univers est considéré comme un système physique. Et nous l'étudierons à l'aide d'équations. Nous pouvons commencer notre exploration de l'univers par quelques observations générales.

Isotropie

Ainsi, la première observation, qui, d'une manière générale, peut ne pas être absolument exacte, tout comme la physique n'est pas absolument exacte, est que l'Univers est isotrope .

L'isotropie signifie que l'univers a la même apparence dans toutes les directions. Bien sûr, cela n'est vrai que pour des distances suffisamment grandes. Si vous regardez de trop près, l'isotropie peut ne pas être observée en raison d'inhomogénéités locales, par exemple, en raison de la forme de notre galaxie.

Uniformité

Si l'Univers est isotrope, alors on peut affirmer avec une grande certitude que l'Univers doit également être homogène . L'homogénéité ne signifie pas l' uniformité dans toutes les directions, mais dans tous les lieux. Autrement dit, à grande échelle, l'Univers a la même apparence, peu importe où se trouve l'observateur - dans notre galaxie ou dans une autre, qui est loin, très loin de nous.

Galaxies

Les galaxies à l'échelle de l'Univers sont effectivement des points de concentration de masse . On peut les traiter comme des points matériels. Le nombre approximatif de galaxies dans la partie visible de l'univers est de cent milliards $$ . À son tour, chaque galaxie contient également environ $$ cent milliards d'étoiles. Nous devons nous rappeler que c'est le nombre de galaxies uniquement à l'intérieur de la sphère que nous pouvons voir. Ce que les astronomes peuvent voir avec des télescopes. C'est-à-dire que le plus éloigné que nous pouvons voir est à une distance de l'endroit où la lumière a réussi à nous atteindre pendant toute l'existence de l'Univers: environ 13 milliards d'années.

Un fait intéressant. Le nombre total d'étoiles dans la partie visible de l'univers $$ , et si chaque étoile a en moyenne 10 planètes, il s'avère $$ - le nombre de planètes Avogadro dans l'univers. Taupe planétaire de substance! (le conférencier rit)

Un argument contre l'homogénéité de l'univers. Réfutation

Considérez un morceau de l'univers où nous sommes. Nous le savons avec certitude, car nous voyons que l'Univers est isotrope . Nous supposons que l'univers est également homogène . Mais que se passerait-il si l'univers n'était pas homogène?

Si l'Univers est isotrope, alors le seul moyen pour qu'il ne soit pas homogène est d'avoir une structure sous la forme d'une sorte de coquilles.


L'hypothèse d'un univers hétérogène. À gauche, un univers isotrope homogène; à droite, un univers isotrope non homogène. La croix au centre nous désigne.

S'il en était ainsi, à tout autre moment, l'Univers n'aurait pas l' air isotrope. Autrement dit, si nous ne voulons pas croire que nous étions en quelque sorte exactement au centre de l'Univers et que l'Univers entier ait une symétrie sphérique autour de nous, alors nous devrons admettre que l'Univers n'est pas seulement isotrope, mais aussi homogène.

Principe cosmologique

Donc, si nous ne croyons pas que nous sommes situés exactement au centre de l'Univers, alors l'Univers doit être homogène. Un Univers homogène signifie que l'Univers est uniformément rempli de particules (galaxies) dans tout le volume. C'est ce qu'on appelle le principe cosmologique . Le principe cosmologique est vrai, car nos observations l'indiquent, bien sûr, à un certain degré d'approximation.

Certains astronomes affirment avoir observé des hétérogénéités à grande échelle dans l'univers. Le conférencier doute de la fiabilité de ces sources et déclarations.

Bien sûr, l'idée de l'homogénéité de l'univers n'est pas absolument exacte. Même le fait qu'il existe déjà des galaxies suggère qu'il existe des hétérogénéités. Soit dit en passant, il n'y a pas seulement des galaxies mais aussi des amas de galaxies. Cependant, à une assez grande échelle, environ de l'ordre du milliard d'années-lumière, l'Univers semble homogène.

Au début, le principe cosmologique n'était qu'un postulat. Mais avec l'accumulation de données d'observation, cela a été confirmé de plus en plus de manière fiable, et à la fin, le rayonnement micro-ondes relique a été découvert, ce qui indique que la distribution initiale de la matière dans l'Univers était très homogène.

Énoncé du problème physique

Il y a un gaz uniforme de particules galactiques. Et chaque galaxie interagit avec d'autres galaxies. Les galaxies dans leur ensemble sont électriquement neutres. Mais ils ne sont pas neutres gravitationnellement. Ils interagissent par la gravité newtonienne. Et c'est la seule force importante à grande échelle. La gravité agit sur les galaxies et essaie de les rassembler.

Donc, si vous regardez n'importe quel point de l'Univers et que vous vous demandez où il doit se déplacer, vous pouvez deviner que de tous les côtés, il est entouré de la même quantité de masse. En suivant cette logique, on peut supposer qu'aucune galaxie ne devrait se déplacer du tout et que l'Univers devrait être statique, car le résultat des forces agissant sur n'importe quel point de l'Univers est nul. C'est absolument faux!

Et maintenant, nous obtenons des équations de mouvement newtoniennes pour l'univers. On pouvait entendre que l'Univers en expansion est en bon accord avec la théorie générale de la relativité d'Einstein, et qu'avant la théorie générale de la relativité, la loi de l'Univers en expansion était incompréhensible. Ce n'est tout simplement pas vrai. C'était peut-être le cas historiquement. Mais ce n'est qu'un fait historique sur les dates, pas sur la logique. Newton pourrait obtenir les équations d'un univers en expansion. Et maintenant, nous allons le faire comme Newton aurait dû le faire.

Système de coordonnées

Dans tout problème physique, la première chose à faire est d'introduire un système de coordonnées. Au lieu de choisir le pas de grille comme distance: 1 mètre, un million de kilomètres, mille années-lumière, nous choisirons une grille pour que ses nœuds soient solidement attachés aux galaxies. Puisque l'univers est homogène, nous pouvons le faire. Ensuite, les galaxies resteront toujours approximativement aux mêmes coordonnées, indépendamment de ce qui arrive à l'univers. Autrement dit, les galaxies semblent être «gelées» dans la grille de coordonnées.

Il n'est pas du tout évident que cela puisse être fait. Si les galaxies se sont déplacées complètement par accident et dans des directions complètement différentes, nous ne pourrions pas le faire. Mais nous voyons que les galaxies se déplacent par hasard. Nous voyons que les galaxies se déplacent de concert, exactement comme si elles étaient intégrées dans une certaine grille de coordonnées. Et ce que nous voyons nous permet de le faire, car les vitesses des galaxies les unes par rapport aux autres sont cohérentes et non accidentelles.

Nous introduisons une grille $$$(x, y, z)$ . Ces coordonnées ne sont pas mesurées en unités de longueur. Si l'on considère deux galaxies séparées par un intervalle $$$\ Delta x$ puis la distance $$$D$ entre eux (en mètres) est exprimé en

$$

$$D = a \, \ Delta x$$

où $$$a$ Est un paramètre d'échelle, qui peut être une constante, mais d'une manière générale, peut ne pas l'être. Le paramètre d'échelle peut dépendre du temps. $$$a = a (t)$ .

Ainsi, par le théorème de Pythagore, la distance entre deux galaxies s'écrit généralement comme

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

Et bien sûr, le paramètre $$$a$ n'est pas une constante. Si c'était une constante, alors les galaxies seraient statiques, elles ne se déplaceraient nulle part. Et ce n'est pas ce que nous observons. On voit qu'ils s'envolent.

Loi Hubble

Nous écrivons la vitesse relative entre deux galaxies. Nous différencions la formule précédente dans le temps. Nous prenons en compte que $$$\ Delta x$ - Il s'agit d'un intervalle fixe, qui ne peut pas être modifié selon les conditions de construction d'un système de coordonnées. Alors

$$

$$\ mathcal {V} = \ dot {a} \, \ Delta x$$

où nous utilisons la notation $$$\ dot {a} = da / dt$ .

Nous écrivons maintenant le rapport de la vitesse relative de deux galaxies à la distance entre elles

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

Notez que $$$\ Delta x$ est réduit, et ce rapport ne dépend pas du tout des coordonnées. Autrement dit, cette formule est valable pour deux galaxies, quelle que soit leur distance ou leur proximité.

Cette relation est appelée paramètre constant de Hubble.

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

et cela ne dépend pas des coordonnées. Ensuite, vous pouvez écrire la même chose sous forme standard

$$

$$\ mathcal {V} = H \, D$$

La vitesse relative de deux galaxies est proportionnelle à la distance qui les sépare.

Vous devez comprendre que nous ne l'aurions jamais écrit si Hubble n'avait pas découvert sa loi. La loi de Hubble, en revanche, n'est pas si surprenante. Il y a un dicton: "Il n'est pas surprenant que le cheval le plus rapide devance tout le monde." Plus vous vous déplacez vite, plus vous êtes loin. Et c'est un fait que Hubble a découvert.

Masse de matière dans l'univers

Considérez un peu de volume $$$\ Delta x \, \ Delta y \, \ Delta z$ . Nous posons une question: quelle masse est concentrée dans ce volume? Soit $$$\ nu$ Est la masse d'une substance dans un volume élémentaire $$$dx \, dy \, dz$ (en kilogrammes). Puis la masse en volume $$$\ Delta x \, \ Delta y \, \ Delta z$ est égal à

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

Quel est le volume métrique de cette zone? Depuis $$$D = a \, \ Delta x$ nous pouvons écrire

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

Quelle est la densité de la substance dans cette zone? Par définition, la densité est $$$\ rho = M / V$ c'est-à-dire en tenant compte des deux formules précédentes, on obtient

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

Il s'agit de la densité physique standard d'une substance.

Bien que la quantité totale de masse en volume $$$\ Delta x \, \ Delta y \, \ Delta z$ ne change pas, puisque les galaxies sont «gelées» dans la grille de coordonnées, la densité absolue de matière dans le même volume peut changer, puisque le paramètre $$$a (t)$ dépend du temps.

Théorème de Newton

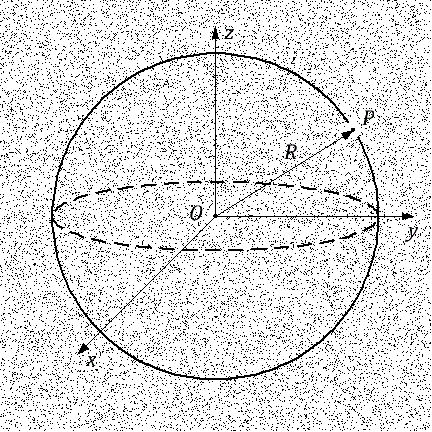Illustration du théorème de Newton

Prenons deux galactites. On peut toujours en mettre un à l'origine. Laissez la galaxie $$$O$ est à l'origine, et la galaxie $$$P$ est à une certaine distance d'elle.

Le théorème de Newton déclare que la force de gravité agissant sur une galaxie $$$P$ dépend uniquement de la quantité de masse à l'intérieur de la sphère centrée à l'origine $$$O$ et traversant la galaxie $$$P$ . La deuxième déclaration du théorème de Newton est que toute la masse à l'intérieur de cette sphère peut être considérée comme concentrée au centre à l'origine au point $$$O$ , à condition que la masse à l'intérieur de la sphère soit répartie, sinon uniformément, au moins de façon isotrope .

En d'autres termes, l'effet de toute la masse à l'intérieur de la sphère sur la galaxie $$$P$ équivalent à comme si cette masse était concentrée en un seul point $$$O$ , qui est le centre de la sphère.

Équations de mouvement newtoniennes

Trouver la distance entre les galaxies $$$P$ et $$$O$ . Galaxie $$$P$ a des coordonnées $$$(x, y, z)$ c'est-à-dire la distance du centre à la galaxie $$$P$ est égal

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

Nous pouvons introduire la notation

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ non mesuré en mètres, mais dans les mêmes unités que $$$x$ , $$$y$ et $$$z$ et ne dépend pas du temps. Alors

$$

$$D = a (t) \, R$$

Nous enregistrons maintenant la vitesse et l'accélération de la galaxie $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Maintenant, nous devons assimiler l'accélération $$$\ mathcal {A}$ à l'accélération associée à toute la masse gravitationnelle à l'intérieur d'une sphère de rayon $$$R$ . Indique la masse de la galaxie $$$P$ pour $$$m$ , et la masse de toute la matière à l'intérieur de la sphère au-delà $$$M$ . Puis la force de gravité agissant sur la galaxie $$$P$ est égal à

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

où $$$G = 6,67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - constante gravitationnelle. Le signe moins dans la formule signifie qu'il s'agit d'une force attractive.

Vous pouvez maintenant enregistrer l'accélération de la galaxie $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Nous assimilons deux expressions pour $$$\ mathcal {A}$ et obtenez

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Nous prenons en compte que $$$D = a \, R$ alors

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Divisez les deux côtés par $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Trouver le volume de la sphère

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

On multiplie le numérateur et le dénominateur du côté droit par $$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

Cette équation est indépendante de $$$R$ , et c'est vrai pour n'importe quelle galaxie de l'univers. Cette équation est l' équation fondamentale centrale de la cosmologie .

L'une des conséquences de cette équation est qu'il est impossible pour l'Univers d'être statique s'il n'est pas vide. De cette équation, il s'ensuit que l'Univers ne peut être statique que s'il est vide.

Nous pouvons réécrire cette équation, étant donné que $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

Cette équation a d'abord été obtenue dans le contexte de la théorie générale de la relativité par Alexander Friedman. Cette équation ne nous dit pas si l'univers est en expansion ou en contraction. Il indique seulement que la dérivée seconde du facteur d'échelle est négative. Autrement dit, si l'Univers se développe, alors il ralentit, et si l'Univers se rétrécit, alors il accélère.

En fait, l'univers est en expansion et ne ralentit pas. Nous avons juste fait ce que Newton pouvait faire et que tous les cosmologistes considéraient comme corrects jusqu'en 1998 environ. Ce modèle a été généralement accepté et a été appelé le modèle standard de l'Univers jusqu'à ce que l'expansion accélérée de l'Univers soit découverte ouvertement. Jusqu'à présent, le côté droit de l'équation n'a qu'un seul terme. En fait, il devrait y avoir plusieurs termes liés à la théorie générale de la relativité.

Vitesse de départ

Maintenant, écris toute l'énergie de la galaxie $$$P$ comme la somme de la cinétique et du potentiel

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D}$$

L'énergie peut être positive ou négative selon le rapport entre ces deux termes. Il est également important de se rappeler que l'énergie totale de la particule $$$P$ enregistré. Si l'énergie totale est positive, la particule ne peut pas revenir en arrière. Une particule ne revient que lorsque l'énergie totale est négative. Le cas limite est l'énergie totale est nulle. Résoudre l'équation $$$E = 0$ pour $$$\ mathcal {V}$ pour trouver la vitesse de départ.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Comme une galaxie $$$P$ l'Univers entier peut avoir une vitesse supérieure à la vitesse de départ, inférieure à la vitesse de départ ou égale à la vitesse de départ. Si la vitesse de l'Univers est supérieure à la vitesse de départ, alors elle se dilate et ne commence jamais à rétrécir; si l'Univers a une vitesse inférieure à la vitesse de départ, alors tôt ou tard, elle commencera à rétrécir.

Réécrire l'équation de l'énergie totale

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Équation de Friedman

Prenons le cas où la vitesse de l'univers coïncide avec la vitesse de départ.

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Simplifiez l'expression: divisez par $$$m$ , multipliez par 2, divisez par $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

Au deuxième terme, on multiplie le numérateur et le dénominateur par $$ . Puis au dénominateur on obtient le volume métrique de la sphère $$$V$ . Étant donné que $$$M / V = ​​\ rho$ nous obtenons

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G \ rho$$

C'est ce qu'on appelle l'équation de Friedman . Elle est équivalente à l'équation newtonienne obtenue ci-dessus. Puisque nous avons supposé que l'énergie totale est nulle, un tel univers se dilate, ralentissant asymptotiquement à zéro, mais ne franchit jamais zéro et ne commence pas à rétrécir.

Rappelons maintenant que $$$\ rho = \ nu / a ^ 3$ . Réécrivez l'équation de Friedman

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

Paramètre $$$\ nu$ très flexible.Cela dépend complètement de notre choix de la grille. Et d'une manière générale, nous pourrions même le choisir pour que$$$\frac{8\pi}{3}\nu G = 1$ . Alors

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

Le côté droit de cette équation est toujours positif, et donc, le taux d'expansion
$$˙ a ne devient jamais égal à zéro. Rappelons maintenant que$\dot{a}$$$˙ a /a=Hestle paramètreconstant deHubble. Il résulte également de l'équation que le paramètre Hubble ne change jamais de signe. Cependant, il continue de ralentir. Le paramètre Hubble devient de moins en moins avec le temps. Cette équation est extrêmement importante pour toute la cosmologie. Un moyen simple de le résoudre est de chercher une solution d'un certain type, à savoir, nous chercherons une solution sous la forme$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

où $$$c$ et $$p sont des constantes.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

Nous avons obtenu une solution à l'équation de Friedman.


Graphique de la solution de l'équation de Friedman

L'univers réel ne suit cette décision que jusqu'à un certain point dans le temps, puis commence à accélérer. Newton pourrait le faire. Il est venu très près. J'ai posé toutes les bonnes questions. Le conférencier est convaincu que Newton, très probablement, l'a fait et a reçu cette décision. Cependant, de telles informations sur l'univers étaient contraires à ses opinions religieuses, et donc il n'a pas publié ses découvertes.