Puis-je gagner au jeu? Simulation Python

Salut les Geektimes.

Dans le processus de l'oisiveté au ralenti, l'idée est venue d'étudier divers jeux d'argent, en même temps pour mieux comprendre comment cela fonctionne. Les résultats, bien que généralement évidents, étaient suffisamment intéressants pour être partagés avec le public.



À qui les détails sont intéressants, je demande sous cat.

Dice: Craps Game

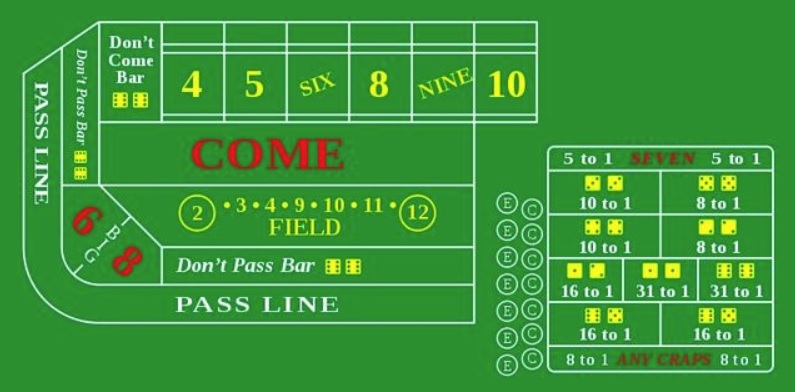
Très probablement, une option intuitivement simple et claire - il y a un cube avec des notes de 1 à 6, et la probabilité qu'un nombre particulier tombe est 1/6. Mais jouer de cette façon serait ennuyeux, donc les jeux avec des règles plus complexes sont populaires. Un jeu de hasard populaire est le craps , l'image ci-dessus montre une image de la table de jeu. Comme vous pouvez le voir, il y a beaucoup de tout, mais nous n'entrerons pas dans des subtilités profondes.

Chaque tour de jeu consiste à lancer deux dés, les points accumulés sont additionnés. Comme le dit l' article , «les règles du jeu sont simples: le joueur lance deux dés, et si la somme des points sur eux est de 7 ou 11, il gagne, si 2, 3 ou 12 perd. Quand un montant différent tombe sur les dés, le tireur les jette dans une combinaison gagnante ou perdante. »

Voyons combien vous pouvez gagner de cette façon. Il n'est pas nécessaire d'aller dans un casino pour cela; nous utiliserons Python pour simuler le jeu. Nous écrivons une fonction pour un jet:

import random def shoot(): return random.randint(1,6) + random.randint(1,6) 

Nous écrirons la fonction de simulation d'un coup selon les règles ci-dessus.

 def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False 

Fixons à notre joueur virtuel un montant initial de 100 $ et commençons le processus de jeu. Laissez notre joueur faire 100 paris, chaque fois 1u.e.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Nous commençons la simulation de 100 parties et nous sommes surpris du résultat, le joueur a gagné , et avec une marge notable de victoires des défaites: Victoire 63, Perte 37, Argent 126. Nous augmentons le nombre de parties à 1000 et recommençons, le joueur a gagné à nouveau: Victoire 680, Perte 320, Argent 460 .

Il est clair que quelque chose ne va pas ici - un jeu dans lequel le joueur serait toujours dans le noir, ne serait guère populaire dans le casino, il ferait simplement faillite. Essayons de le comprendre.

Il semble intuitivement qu'en lançant un dé, la probabilité de chute d'une facette est également probable. Et cela est vrai, mais dans le cas d' un cube. S'il y a deux cubes, alors tout devient plus compliqué. Par exemple, le nombre 7 peut tomber comme 3 + 4, 2 + 5, 1 + 6, mais le nombre 12 ne peut tomber que comme une combinaison de 6 + 6.

Dans le cahier Jupyter, nous construisons un calendrier pour la perte de montants de 1 à 12 pour 100 lancers:

 from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y) 

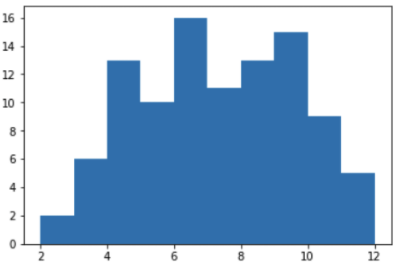
L'hypothèse a été confirmée et le montant du centre tombe vraiment plus souvent. Ainsi, les nombres 7 et 11 tombent vraiment plus souvent que 2,3 ou 12. Et la probabilité d'obtenir une combinaison gagnante "7 ou 11" est vraiment plus élevée.

Comment est-ce possible? Hélas, la réponse est simple - l'auteur de l'article cité ci-dessus n'a tout simplement pas bien compris les règles du jeu. Le texte "les règles du jeu sont simples: le joueur lance deux dés, et si la somme des points sur eux est 7 ou 11, il gagne, si 2, 3 ou 12 - il perd " est très loin de la vérité, et les règles dans le craps ne sont pas aussi simples qu'elles semblent .

Les vraies règles pour parier sur la ligne de passe se sont avérées un peu plus compliquées (il existe d'autres types de paris, ceux qui le souhaitent peuvent le découvrir par eux-mêmes).

Déplacer 1 : Un jet est fait. Si 7 ou 11 tombent, le joueur gagne; si 2, 3 ou 12, le joueur perd. Si un autre numéro tombe, il est mémorisé sous le point de nom.

Déplacer 2 : Un jet est fait. Si 7 tombe, le joueur perd. Si le point tombe, alors le joueur a gagné. Si d'autres numéros tombent, le mouvement est répété (à ce moment, les joueurs peuvent également parier sur d'autres numéros).

En effet, tout est un peu plus compliqué que décrit dans la version originale. Nous ajoutons une fonction de simulation prenant en compte des règles plus précises.

 def move(): point = 0 while True: val = shoot() if point == 0: # First move if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False point = val else: # 2..N move if val == 7: return False if val == point: return True 

Le résultat est désormais plus proche de la vérité: pour 100 matchs, le joueur a gagné 43 fois, perdu 57 fois, le solde en fin de partie était de 86.u. par rapport au 100 d'origine. Il est également intéressant de noter que le nombre de victoires s'est avéré assez important et n'est que légèrement inférieur à 50%. C'est une stratégie compétente du point de vue du casino - elle vous permet de maintenir l'intérêt du participant dans le jeu (il serait inintéressant de perdre tout le temps), mais en même temps, le solde des bénéfices du casino reste positif et le solde d'argent du joueur est par conséquent négatif.

Voyons plus en détail ce qui est obtenu pour la simulation de 100 jeux.
- La chance de gagner à la première étape est tombée dans une vingtaine de cas.
- La chance de perdre immédiatement au premier échelon est tombée dans 15 cas.
- Dans les 65 cas restants, le jeu continue, et tout est délicat: le choix vient de deux nombres, 7 et un point, mais comme vous pouvez le voir sur le graphique ci-dessus, la probabilité de chute d'un numéro 7 est maximale, ce qui en général devait être prouvé.

Il est intéressant de noter que les chances de gagner à 45% sont plutôt élevées. Est-il donc possible de gagner? À court terme, par exemple, dans une autre simulation, le joueur a été «chanceux», et en 100 matchs, il a augmenté son capital virtuel de 100 à 112ye.



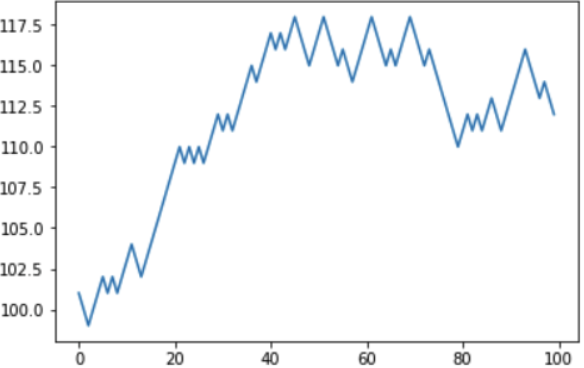
Mais déjà la prochaine simulation a montré un bilan négatif: le joueur a réduit son état de 100 à 88ye, ayant d'ailleurs perdu le même 12ye "gagné" la fois précédente.

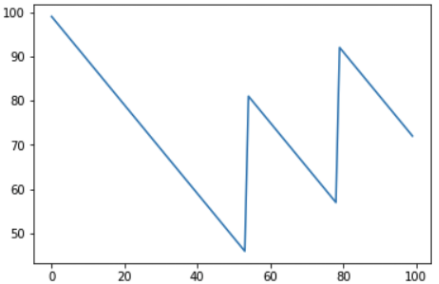
Si vous augmentez le nombre d'itérations à 1000, vous pouvez voir à quoi le solde monétaire du joueur peut ressembler à long terme:



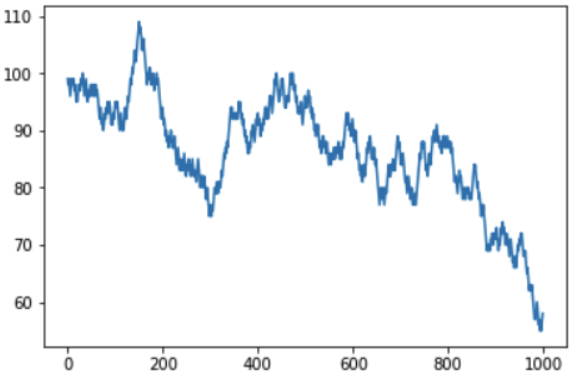
Il est clair qu'avec une chance de gagner chaque partie à moins de 50%, le montant d’argent résultant sur le compte du joueur diminuera progressivement et le montant des bénéfices du casino augmentera progressivement. Soit dit en passant, sur le graphique, des éclats et des chutes sont visibles, et une question raisonnable peut se poser - peut-on les prévoir? Hélas, non, car Les lancers de dés sont des événements indépendants les uns des autres, et les résultats précédents n'affectent en rien les éléments suivants. Vous pouvez répéter l'idée principale une fois de plus - vous pouvez gagner une ou même plusieurs fois, mais à long terme, il est impossible de rester dans le plus au casino, les règles du jeu sont établies de sorte que le solde ne soit pas en faveur du joueur.

Il existe d'autres types de paris dans le jeu de craps, et ceux qui le souhaitent peuvent les analyser par eux-mêmes.

Roulette américaine

Le prochain type de jeu populaire est la roulette, considérez sa version américaine.



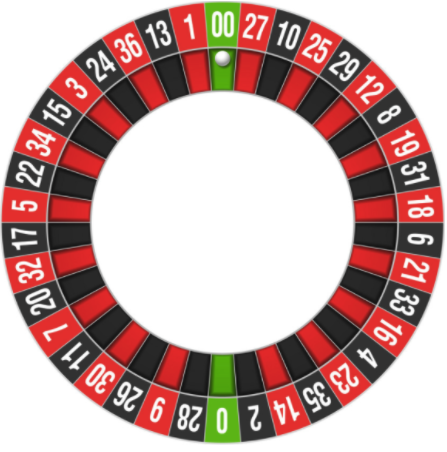
Le terrain de jeu de la roulette est divisé en 38 cellules: 36 zones avec des nombres + 2 zones «zéro» et «double zéro». Une balle lancée sur une roulette s'arrêtera évidemment dans l'une des zones. Le joueur peut faire une variété de paris, dont il existe plus de 10 types, envisagez certains d'entre eux.

Noir-rouge (ou pair-impair)

Un joueur gagne si la mise qu'il nomme coïncide. Évidemment, la probabilité de noir ou de rouge serait de 50/50, s'il n'y avait pas deux champs de zéro - s'ils les touchent, le pari est perdu. Comme dans le cas du craps, cela rend la probabilité de gagner légèrement inférieure à 50% - mais ce «légèrement» suffit pour être dans le rouge.

Nous écrirons la fonction de simulation du déplacement en utilisant des nombres aléatoires de 1 à 38, les 2 derniers chiffres seront considérés comme «zéro».

 def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0 

Exécutez la simulation pour 100 jeux, le code est le même que dans la simulation de craps, nous ne changeons que l'appel de fonction.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Résultat: en 100 tentatives, le joueur a gagné 46 fois et perdu 54 fois. Le graphique montre que le joueur a connu des «hausses» et des «chutes», mais le solde final est toujours négatif.



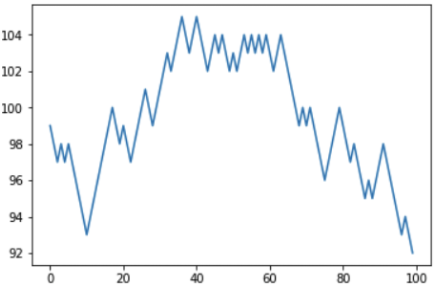
Plus nous jouons, plus nous allons profondément dans le moins, et le casino, respectivement, dans le plus:



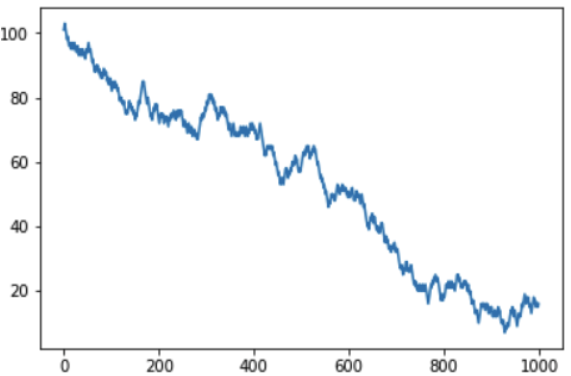
Le lecteur a demandé pourquoi je ne considérais pas la roulette européenne avec un champ «zéro» - comme vous pouvez le deviner, les chances de gagner là-bas sont vraiment plus élevées, mais le principe général ne change pas. En fait, la différence réside uniquement dans la «vitesse de perte». Voici le calendrier commun des versions américaine et européenne du jeu:


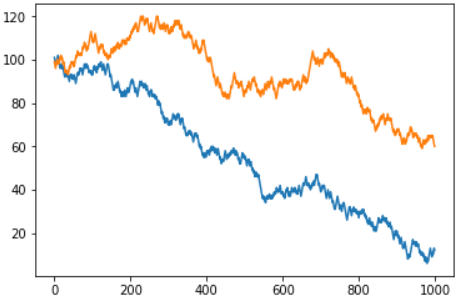
Ceux qui veulent tester la version européenne de la roulette avec 37 emplacements peuvent utiliser la deuxième option de la fonction:

 def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0 

Pariez sur un numéro précis

Le joueur peut également parier sur un certain nombre, le pari sur la victoire est de 35: 1. Cela semble génial, mais il est facile de deviner que la probabilité de chute d'un certain numéro de roulette est de 1:38, c'est-à-dire encore une fois, un peu moins.

Ajoutons la fonction de pari à un numéro spécifique:

 def move_roulette2(num): val = random.randint(1,38) return val == num 

Simulation, nous supposons que le joueur met le numéro 10:

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

En conséquence, le joueur a gagné 2 fois et perdu 98 fois, le solde final est de -28.u.



Misez sur deux numéros

Vous pouvez parier sur deux numéros - les chances de gagner sont plus élevées, mais le pari est moindre et est de 17: 1.

Écrivons une fonction:

 def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2 

Pour 100 tentatives de notre simulation, le joueur a gagné 3 fois et perdu 97 fois, le solde était de -46u.e.

Il existe d'autres types de paris, par exemple, pour 4 numéros avec un coefficient de 1: 8, ceux qui le souhaitent peuvent expérimenter par eux-mêmes. Comme vous pouvez le deviner, toutes les chances sont conçues pour que le joueur soit dans le rouge. Il semble tentant de mettre 1ye sur le nombre pour gagner autant que 35ue. Mais le montant des gains augmente de 35 fois, et les chances de gagner diminuent de 38 fois - le solde final sera toujours en faveur du casino.

Loto 6 sur 45

La prochaine chose intéressante à vérifier est le loto. Le principe du jeu est assez simple - il y a 45 balles dans le tambour, 6 d'entre elles tombent au hasard. Le prix du billet selon le site Web de Gosloto est de 100 roubles, et le prix dépend du nombre de boules devinées. L'ordre approximatif des gains est le suivant: 2 boules devinées donnent une victoire de 100r, 3 boules devinées donnent 300r, 4 boules - 3000r, 5 boules - 300.000r et 6 boules - un super prix d'environ 10.000.000r.

Tout d'abord, écrivez un programme pour lancer des balles et comparer le résultat:

 def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res) 

Une balle aléatoire «obtient» 6 fois du tableau des boules, puis le nombre d'éléments d'intersection de deux ensembles est déterminé. Nous allons maintenant construire un graphique du gain total sur le nombre de billets achetés. Pour simplifier, nous supposons que le joueur mise sur les mêmes numéros.

 money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money) 

Pour comprendre l'ordre de grandeur: si vous achetez 100 billets (le montant total dépensé sera de 10 000 r), cela donne 14 boules "doubles" devinées et une "triple" devinée. Le gain total est d'environ 2000r avec 10 000r dépensés.

Le calendrier de paiement pour le montant dépensé est presque linéaire:



Il s'avère que si vous achetez des billets par million, le gain sera de 250 000. Le «super prix» de la simulation n'est jamais tombé, bien que théoriquement, cela soit certainement possible. Soit dit en passant, comme il est écrit dans les règles, la cagnotte est de 50% des billets vendus, mais le «super prix» ne tombe pas toujours, de même qu'avec le casino, les organisateurs, bien sûr, gagnent toujours.

Machines à sous

Ils fonctionnent également sur un principe (pseudo) aléatoire, «pseudo» car Le code en eux a longtemps été programmatique et n'a pas de mécanique propre. Les principes généraux décrits ci-dessus pour les machines à sous fonctionnent également, et les graphiques ne seront probablement pas différents, ceux qui le souhaitent peuvent ajouter eux-mêmes la fonction de simulation.

Un bon article sur la conception des machines à sous a déjà été publié sur Geektimes.

Conclusion

Cet article n'a peut-être pas ouvert l'Amérique à beaucoup, mais sur les graphiques, il est, en principe, plus visuel. Il s'est avéré plus intéressant de comparer une approche psychologique fondamentalement différente du jeu. Les gains à la loterie sont potentiellement importants, mais très rares. Dans les casinos, l'approche est l'inverse - les paris sont configurés pour qu'une personne gagne le plus souvent possible. Conditionnellement, après avoir fait 10 jeux dans un casino, une personne gagnera 4 fois et perdra 6 fois. Cela permet au joueur de ne pas se désintéresser du jeu, mais dans tous les cas, l'équilibre global reste négatif - une personne gagnera plusieurs fois, mais perdra également un peu plus .

C'est peut-être déjà si évident, mais l'article ne concerne que les jeux basés sur le hasard, pas sur le poker, les cartes, les échecs, etc. Peut-il y avoir une «stratégie gagnante» dans de tels jeux aléatoires? Evidemment non, car ni os, ni balle, ni billets de loterie n'ont de mémoire, et leur comportement ne dépend pas des itérations précédentes. Soit dit en passant, il est important de se souvenir de ce moment - intuitivement, après avoir perdu plusieurs fois, une personne peut décider qu'il va maintenant «définitivement» gagner. Hélas, il n'y a pas de roulette ni de dé, et ils ne connaissent pas le nombre de tentatives précédentes, chaque partie commence essentiellement par une table rase.

Répondre à la question dans le titre de l'article - est-il possible de gagner au jeu? Comme le montre la simulation, en principe c'est possible, admet la théorie des probabilités. Mais pas pour longtemps - cela vaut la peine de commencer à jouer la 2e, 3e, ... Nième fois, car l'équilibre diminue. À long terme, gagner dans un casino est impossible.

PS: Pour ceux qui veulent expérimenter, le code source dans un fichier est disposé sous le spoiler. Il peut être exécuté dans l'IDE Python en ligne, par exemple ici . Pour tester la version européenne de la roulette au lieu de la version américaine, il suffit de changer 38 à 37 dans le code. Cette simulation est assez basique et ne prend pas en compte divers facteurs supplémentaires, tels que le montant d'argent d'un joueur ou la limite des paris dans un casino, ceux qui le souhaitent peuvent ajouter tout cela indépendamment. Sous le spoiler, vous pouvez également regarder une version vidéo de cet article.