Blague à part, le sujet est grave, le risque d'incendie. Allons-y. Il s'agit du troisième article de la série, il aborde les modèles d'estimation du courant maximum de la piste imprimée, qui dans certaines situations est un paramètre déterminant lors du choix de l'épaisseur des couches conductrices de la carte de circuit imprimé.
Dans un article
précédent, il a été dit que le choix de l'épaisseur des couches de cuivre de la carte de circuit imprimé est déterminé, tout d'abord, par le jeu minimum requis et la largeur minimale du conducteur, ainsi que par le courant maximal traversant le conducteur. Ces paramètres peuvent se contredire: plus la couche conductrice est mince, plus le motif topologique est petit, mais plus le courant maximal que le chemin d'impression peut supporter est petit (ceteris paribus, la largeur du conducteur, la fréquence du courant, le dissipateur de chaleur, etc.). L'énergie thermique Q libérée sur la résistance ohmique R de la piste imprimée (chaleur Joule Q = I
2 Rt, où I est la force du courant, t est le temps) entraîne une augmentation de sa température par rapport à l'environnement, entraînant une surchauffe du conducteur lui-même et des composants associés, ou, en dernier recours, à son extinction à un courant limite (courant de fusion anglais). La corrélation entre le courant à travers la piste d'impression et l'augmentation de température dépend de nombreux paramètres et est en général difficile à imaginer, cependant, il existe des formules qui nous permettent de faire des estimations préliminaires.
Price, Onderdonk et Brooks
L'une des premières tentatives a été faite par W.H. Pris (WHPreece). Il a reçu sa dépendance empirique dans une expérience de laboratoire dans laquelle il a progressivement augmenté le courant à travers le conducteur jusqu'à ce qu'il devienne rouge. La formule Pris relie le courant de préchauffage au diamètre du conducteur d pour différents matériaux:
où K est une constante tabulaire approximativement égale à 80 pour le cuivre. En utilisant le rapport de l'aire du cercle, nous pouvons réécrire cette formule pour le cas d'un conducteur en cuivre avec une aire de section S:
Dans l'expérience Pris, le conducteur était suspendu dans l'air, contrairement à un conducteur sur une carte de circuit imprimé, pour lequel les conditions du dissipateur de chaleur sont complètement différentes. Les conditions du dissipateur de chaleur sont plus proches pour les cas d'un seul conducteur de connexion, ainsi que pour certains cas de soudage par microfils (lorsque la composition n'est pas utilisée pour le protéger), où cette formule peut donner une bonne estimation du courant de limitation.
L'augmentation acceptable de la température de la piste d'impression est généralement considérée comme étant de 10 à 30 ° C. Cette valeur peut être supérieure en fonction des paramètres du projet, cependant, sur toute la plage de températures de fonctionnement du produit, la température de la piste doit être inférieure à la température de transition vitreuse du matériau de la carte de circuit imprimé (température de transition vitreuse anglaise, T
g ) et, surtout, la température du cuivre. Par conséquent, la dépendance de l'augmentation de température ∆T du courant I de la piste imprimée de largeur w et d'épaisseur de feuille h, utile par Brooks dans [1], est utile:
où C, α, β, γ sont des constantes, dont les valeurs pour les couches externes et internes sont données dans le tableau 1. Il convient de garder à l'esprit que sur les couches externes, l'épaisseur de la feuille est généralement de 20 à 40 microns supérieure à la valeur de base en raison de la pulvérisation supplémentaire lors de la création de la transition trous. De plus, l'effet de la finition sur les planches sans masque peut être significatif. Ceci est utilisé dans les appareils électriques, lorsqu'une soudure supplémentaire est soudée à la piste imprimée ouverte depuis le masque.
Une autre formule bien connue pour calculer la capacité de charge de courant ultime d'un conducteur est la formule d'Onderdonk (anglais IMOnderdonk), qui contient un paramètre aussi important que le temps. Elle rapporte le temps t du passage du courant I à travers un conducteur en cuivre de section S et l'augmentation de température ∆T par rapport à la température initiale T
0 :
Étant donné que dans la dérivation de la formule [2], toute évacuation de chaleur est exclue, pour le cas d'une piste d'impression, cette formule est applicable pour une impulsion de courant courte pouvant durer jusqu'à 1-2 secondes. Avec l'augmentation du temps et l'influence de l'évacuation de la chaleur, la précision de l'estimation diminue, ce qui réduit considérablement le courant limite. Les graphiques de dépendance pour les trois formules ci-dessus pour divers paramètres de la piste d'impression sont représentés sur les figures 1 et 2.
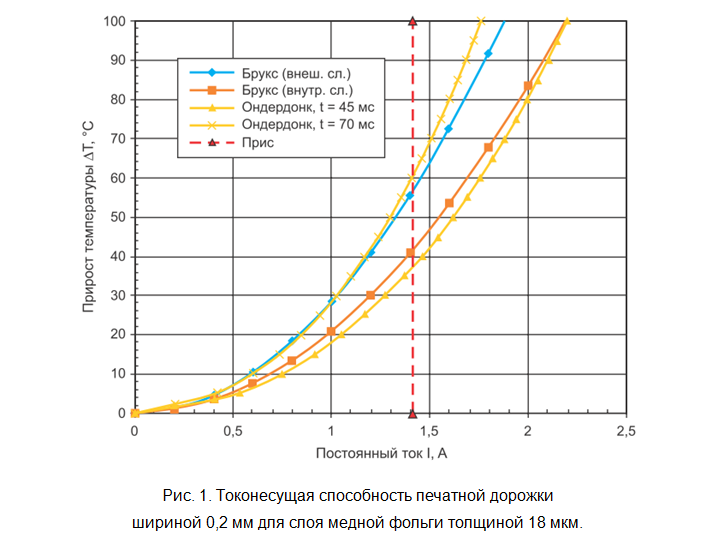

Il est toujours important de considérer les conditions expérimentales ou les hypothèses analytiques dans la dérivation afin de comprendre les limites d'applicabilité d'une formule particulière. Aucune des formules ci-dessus ne donnera une relation exacte et optimale entre le courant limite et la section transversale requise du conducteur pour des applications réelles. La même chose s'applique aux calculatrices simples qui peuvent être trouvées sur Internet (
par exemple ), car elles sont basées sur ces formules ou sur des formules similaires. L'influence des conducteurs et composants voisins en tant que sources et récepteurs de chaleur, de rayonnement, de refroidissement actif ou passif ne peut être prise en compte que lors de la modélisation thermoélectrique dans des systèmes de CAO spécialisés (tels que Cadence, ANSYS et autres). Cependant, même dans ce cas, les résultats de la modélisation et de l'expérience peuvent varier considérablement. Le fait est que la piste d'impression n'a pas de section rectangulaire, mais est proche de trapézoïdale (Fig.3), et sa largeur et sa valeur de conductivité de feuille de cuivre peuvent non seulement différer de celles calculées par le modèle, mais aussi avoir une certaine dispersion d'un échantillon à l'autre, lot au lot, fabricant à fabricant, etc. L'influence des écarts de largeur augmente avec sa diminution. Néanmoins, les résultats calculés par des formules et des recommandations des normes représenteront le plus souvent le pire des cas, offrant ainsi une marge de sécurité au système. Si le développeur a besoin d'optimiser le rapport entre le courant limite et la section requise de la piste imprimée, alors il est nécessaire d'aller vers cet objectif par voie itérative de modélisation et d'expérimentation.

Effet cutané
Une augmentation de la section transversale de la piste imprimée réduit proportionnellement sa résistance ohmique par unité de longueur, ce qui réduit les pertes de chaleur pendant le flux de courant continu. La situation avec le courant alternatif n'est pas si simple en raison de l'existence d'un effet de peau (effet de peau anglais), ce qui conduit au fait que la densité du courant alternatif est inégalement répartie sur la section du conducteur, décroissant exponentiellement à zéro de la surface du conducteur au centre. Pour la commodité des calculs, le concept de la section efficace du conducteur avec une profondeur déterminée par le rapport est utilisé:
où f est la fréquence actuelle, σ est la conductivité du métal, μ est la perméabilité magnétique. A une profondeur égale à δ, la densité de courant devient e fois inférieure à la densité de courant sur la surface J
S. Mathématiquement, l'égalité approximative suivante peut être montrée pour la densité de courant J (x, y) dans le conducteur:
Autrement dit, pour des calculs approximatifs, nous pouvons supposer que le courant ne circule que dans la couche limite du conducteur de périmètre l de profondeur δ, et avec une distribution uniforme (figure 4).

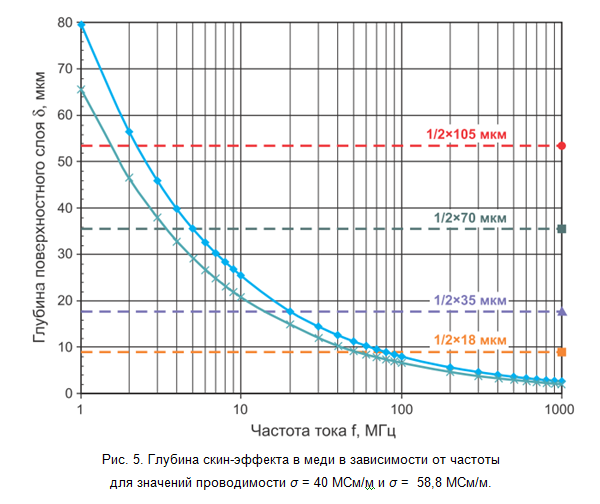
Dans le cadre de ce modèle simplifié, si la profondeur de la couche de surface est inférieure à la moitié de l'épaisseur de la piste d'impression, l'impédance de la piste d'impression à une fréquence donnée sera déterminée par cette section efficace, entraînant une augmentation de la résistance ohmique et une légère diminution de l'inductance. Dans la fig. La figure 5 montre la dépendance de la profondeur de la couche superficielle de la fréquence du courant en tenant compte de la propagation de la conductivité du cuivre déposé. On peut en déduire que pour les couches de cuivre de 18 μm d'épaisseur, la fréquence de coupure (au-dessus de laquelle l'effet peau joue un rôle) est de l'ordre de 50-70 MHz, et pour les couches de 35 μm d'épaisseur elle est de l'ordre de 15-20 MHz. Notez qu'à des fréquences supérieures à 100 MHz, la profondeur de l'effet de peau varie légèrement, ce qui nous permet de négliger sa dépendance à la fréquence dans les calculs des signaux haute fréquence.
Lors de la conception de circuits imprimés avec des courants constants de plusieurs ampères, il est nécessaire d'effectuer des calculs thermiques pour les composants électriques et les conducteurs. Les modèles présentés et les relations analytiques nous permettent d'estimer le courant maximal des pistes imprimées et, sur sa base, de sélectionner l'épaisseur nécessaire des couches de cuivre et la topologie des conducteurs. Pour obtenir la solution exacte, il est nécessaire d'utiliser des systèmes de CAO spécialisés, tandis qu'il est souhaitable de spécifier la géométrie en tenant compte des erreurs de fabrication et des données de conductivité du cuivre reçues du fabricant des cartes de circuits imprimés. Je recommande fortement de lire les
articles de D. Brooks consacrés à une analyse détaillée des méthodes d'estimation de la température des conducteurs imprimés, qui fournissent des résultats visuels de la modélisation des champs de température.
Littérature
[1] Brooks DG, Adam J. «Trace Currents and Temperatures Revisited», UltraCAD, 2015.
[2] Adam J., Brooks DG, «À la recherche de Preece et Onderdonk», UltraCAD, 2015.
L'article a été publié pour la première fois dans la revue Components and Technologies 2018, n ° 1. La publication sur Geektimes a été approuvée par les rédacteurs du magazine.