Quelles tâches sont bien adaptées à la recherche scientifique?

Quel numéro faut-il insérer dans le dernier triangle?

Les scientifiques résolvent les problèmes; tel est leur travail. Mais quelles tâches seront des sujets de recherche prometteurs? Pour répondre à cette question, j'ai écrit le livre Lost in Mathematics , où j'ai examiné les problèmes liés aux bases de la physique.

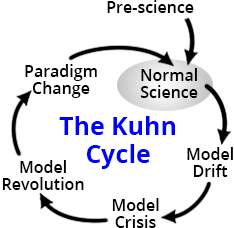
La première classification approximative des problèmes de recherche peut être organisée en utilisant le cycle de développement des théories scientifiques de Thomas Kuhn. Le cycle de Kuhn se compose d'une phase de «science ordinaire», suivie d'une «crise» conduisant à un changement de paradigme, après quoi une nouvelle phase de «science ordinaire» commence. Ceci est une incroyable simplification de la réalité, mais convient pour un raisonnement ultérieur.

Tâches courantes

Au cours de la phase scientifique ordinaire, les questions de recherche peuvent généralement être formulées comme "Comment pourrions-nous mesurer cela?" (pour les expérimentateurs) et "Comment pourrions-nous calculer cela?" (pour les théoriciens).



Les bases de la physique sont pleines de ces «problèmes ordinaires». Les expérimentateurs ont de nombreux problèmes, car tous les problèmes faciles à résoudre ont déjà été résolus et la complexité de la mesure de quelque chose de nouveau ne cesse de croître. Les problèmes des théoriciens proviennent du fait que les prédictions en physique ne sortent pas des hypothèses par elles-mêmes. Il est souvent nécessaire de passer par de nombreuses étapes d'argumentation et de faire de nombreux calculs longs pour arriver aux conséquences numériques des hypothèses théoriques.

Un bon exemple d'un problème courant dans les bases de la physique serait la matière noire froide. L'hypothèse est assez simple: dans l'espace il y a quelque chose de froid et d'obscur qui se comporte comme un liquide et interagit faiblement avec lui-même et avec d'autres matières. Mais cela en soi n'est pas une prédiction particulièrement utile. Une bonne tâche de recherche serait: "Comment la matière noire froide affecte-t-elle les fluctuations de température du CMB?" Et puis vient la question expérimentale: "Comment mesurer cela?"

D'autres tâches de ce type dans les principes fondamentaux de la physique sont: "Quelle est la contribution de la gravité au moment magnétique d'un muon?" et "Quel est l'arrière-plan de la diffusion des photons dans le Grand collisionneur de hadrons?"

Les réponses à ces tâches courantes élargissent notre compréhension des théories existantes. Ces calculs peuvent être effectués dans nos plates-formes existantes, mais ils peuvent être assez compliqués.

Les tâches données dans les paragraphes précédents à titre d'exemples sont résolues, ou du moins nous savons les résoudre, bien qu'il soit toujours possible d'exiger une précision améliorée. Mais dans cette catégorie, il y a aussi des problèmes non résolus.

Par exemple, la théorie quantique de l'interaction nucléaire forte devrait prédire les masses de particules constituées de plusieurs quarks - neutrons, protons et autres particules composites similaires (mais instables). Mais de tels calculs sont sacrément compliqués. Aujourd'hui, ils sont effectués à l'aide de programmes informatiques complexes - calculs sur réseau - et leurs prévisions ne sont toujours pas aussi bonnes. Une question connexe est de savoir comment la matière nucléaire se comporte dans les noyaux des étoiles à neutrons.

Ce ne sont que des exemples choisis au hasard de nombreuses questions ouvertes de physique, qui sont des «problèmes normaux», qui, comme on le croit, peuvent être trouvés dans le cadre de théories que nous connaissons déjà - mais, je pense, ils illustrent bien ce sujet.

Si nous allons au-delà des bases, nous avons alors des tâches normales comme prédire les cycles solaires et le temps ensoleillé - elles sont compliquées en raison de l'extrême non-linéarité et des turbulences partielles du système, mais nous ne nous attendons pas à ce qu'elles entrent en conflit avec les théories existantes. Il existe toujours une supraconductivité à haute température, un phénomène bien étudié, mais théoriquement insuffisamment compris, car ces matériaux manquent de quasiparticules. Et ainsi de suite.

Ce sont les tâches que nous étudions lorsque tout se déroule comme prévu. Mais il existe encore des tâches qui, en principe, peuvent changer de paradigme, tâches qui signalent l’existence d’une «crise» dans la terminologie de Kuhn.

Tâches de crise

Les tâches de crise évidentes sont des observations qui ne peuvent être expliquées sur la base de théories bien connues.

Je ne considère pas la majorité des observations liées à la matière noire et à l'énergie noire comme des crises. La plupart de ces données peuvent être assez bien expliquées en ajoutant simplement deux nouvelles composantes au budget énergétique de l'univers. Bien sûr, vous vous plaindrez que cela ne nous donnera pas une description microscopique, mais nous ne disposons pas de données sur les structures microscopiques, par conséquent, nous ne pouvons toujours pas formuler le problème.

Mais certaines observations de matière noire appartiennent à la "crise". Corrélations inexplicables, modèles dans les galaxies, qui sont difficiles à expliquer à l'aide de la matière noire froide, par exemple, la dépendance de Tully-Fisher , ou l'étrange capacité de la matière noire à suivre la distribution de la matière. Pour ces observations, il n'y a pas d'explication satisfaisante basée sur des théories bien connues. La modification de la gravité explique avec succès certains d'entre eux, mais pose d'autres problèmes. Voilà pour la crise! Et c'est une bonne crise, j'ose le dire, car nous avons des données qui s'améliorent de jour en jour.

Ce n'est pas le seul bon problème d'observation de crise qui existe dans les fondamentaux de la physique. L'un des plus anciens, mais toujours bien vivant, est le moment magnétique du muon . Nous avons un écart de longue date entre les prévisions théoriques et les mesures, qui n'est toujours pas résolu. De nombreux théoriciens considèrent cela comme un signe qu'il ne peut pas être expliqué dans le cadre du modèle standard, et donc une nouvelle théorie améliorée est nécessaire.

Il y a quelques problèmes similaires et plutôt persistants. Par exemple, l'expérience DAMA . Dans cette expérience, les scientifiques recherchent de la matière noire. Ils reçoivent un signal d'une source inconnue avec une modulation annuelle, et le suivent depuis plus de dix ans. Il y a certainement un signal, mais s'il s'avère que c'est de la matière noire, le résultat entrera en conflit avec d'autres résultats expérimentaux. En conséquence, DAMA voit quelque chose, mais personne ne sait exactement quoi.

Il y a toujours des observations déroutantes de l'expérience LSND sur les oscillations des neutrinos qui ne sont pas cohérentes avec toute autre combinaison de paramètres. Il existe également une étrange différence dans les résultats des mesures du rayon du proton à l'aide de deux méthodes différentes, ainsi qu'une autre histoire similaire avec la durée de vie des neutrons . Il y a également eu récemment des incohérences dans la mesure du paramètre Hubble à l'aide de différentes méthodes, et cela peut ne pas en valoir la peine, mais cela peut valoir la peine de s'inquiéter.

Bien entendu, chacune de ces anomalies dans les données peut avoir une explication «normale». Il peut s'agir d'une erreur de mesure systématique ou d'une erreur de calcul ou d'un ingrédient manquant. Mais peut-être, c'est peut-être quelque chose de plus.

Il s'agit d'un type de «problème de crise» - le conflit entre la théorie et l'observation. Mais à côté de cela, il y a des problèmes de crise d'un tout autre genre, situés du côté de l'évolution des théories. Ce sont des problèmes de cohérence interne.

Le problème de la cohérence interne se pose lorsque votre théorie prédit des observations contradictoires, ambiguës ou dénuées de sens. Un exemple typique de ceci est les probabilités qui deviennent supérieures à l'unité, ce qui ne coïncide pas avec l'interprétation de la probabilité. C'est à cause de ce problème que les physiciens étaient convaincus que le LHC nous ferait la démonstration d'une nouvelle physique. Ils ne savaient pas si ce serait Higgs, et cela pourrait être autre chose - par exemple, un changement inattendu dans une faible interaction nucléaire - mais il s'est avéré que c'était Higgs. La restauration de la cohérence interne a conduit à une prédiction réussie.

Historiquement, l'étude des problèmes de cohérence a conduit à de nombreuses percées marquantes.

Un exemple d'un tel problème est la " catastrophe ultraviolette " dans laquelle une source de chaleur devrait émettre une quantité infinie de lumière à de courtes longueurs d'onde. Cela ne correspond clairement pas à une théorie physique significative dans laquelle les quantités observées doivent être finies. (Notez que ce conflit survient avec l'hypothèse. Mathématiquement, il n'y a rien de mal à l'infini). Planck a résolu ce problème et la solution a finalement conduit au développement de la mécanique quantique.

Un autre problème célèbre de cohérence est que la mécanique newtonienne s'est avérée incompatible avec la symétrie de l'électrodynamique espace-temps. Einstein a résolu ce désaccord et a reçu une théorie spéciale de la relativité. Dirac a ensuite résolu la contradiction entre la mécanique quantique et STR, qui a conduit à la création de la théorie des champs quantiques. Einstein a éliminé les contradictions supplémentaires entre SRT et la gravité newtonienne, et a reçu GR.

Tous ces problèmes étaient bien définis et spécifiés.

Mais la plupart des problèmes théoriques actuels dans les principes fondamentaux de la physique ne sont pas de ce type. Oui, ce serait bien si les trois interactions du modèle standard pouvaient être combinées en une seule. Ce serait bien, mais ce n'est pas nécessaire pour la cohérence. Oui, ce serait bien si l'Univers était supersymétrique. Ce serait bien, mais ce n'est pas nécessaire pour la cohérence. Oui, ce serait bien si nous pouvions expliquer pourquoi la masse de Higgs est techniquement contre nature. Mais il n'y a pas de contradiction dans le fait que la masse de Higgs est ce qu'elle est.

Le fait qu'Einstein, et plus encore Dirac, aient été inspirés par la beauté de ses théories est bien décrit. Dirac aimait particulièrement louer l'utilisation de l'élégance mathématique dans le développement des théories. Mais leur motivation personnelle nous intéresse dans la mesure où. Rétrospectivement, nous comprenons qu'ils ont réussi parce qu'ils ont initialement pris de bonnes tâches.

Il y a peu de vrais problèmes théoriques dans les fondements de la physique aujourd'hui, mais ils existent. L'un d'eux est le manque de quantification de la gravité. Il est mathématiquement impossible de simplement ratisser ensemble le modèle standard et la relativité générale, et nous ne savons pas comment le faire correctement.

Un autre problème sérieux avec le modèle standard est le pôle de Landau dans l'une des constantes de couplage . Cela signifie que la force de l'une des interactions devient infinie. Ce n'est pas un résultat physique, tout comme une catastrophe ultraviolette, donc quelque chose doit se produire ici. Peu d'attention a été consacrée à ce problème, car la plupart des théoriciens pensent que le modèle standard est uni bien avant d'atteindre le pôle Landau, ce qui rend l'extrapolation redondante.

Il existe encore des cas où le type de tâche à accomplir n'est pas clair. L'un d'eux est la non-convergence de l'expansion perturbative. Peut-être que la seule question est d'améliorer l'appareil mathématique, ou, peut-être, nous comprenons complètement la théorie quantique des champs. Le même cas avec le théorème de Haag . Il m'est également difficile de classer le problème de mesure en mécanique quantique. Un appel aux processus macroscopiques dans les axiomes de la théorie est incompatible avec les idéaux des réductionnistes, mais, encore une fois, ce n'est pas un problème fondamental, mais une préoccupation conceptuelle. Donc, sur cette question, je suis en difficulté.

Cependant, la leçon que nous apprend l'histoire des problèmes de crise est claire: les problèmes sont des sujets de recherche prometteurs s'ils sont réellement des problèmes. Autrement dit, vous devez être capable de formuler une contradiction mathématique. Si le problème est simplement que vous n'aimez pas un certain aspect de la théorie, vous perdrez probablement votre temps.