L'échec de la version élégante originale de la structure de l'univers

Les huit planètes de notre système solaire et de notre soleil, observant l'échelle de leurs tailles, mais pas l'échelle de leurs orbites. À l'œil nu, la chose la plus difficile à voir est Mercure. Toutes les planètes se déplacent sur des orbites elliptiques.

Les meilleures théories scientifiques sont simples, simples, prédisent efficacement les résultats des observations et contiennent une élégance intérieure. Les équations les plus simples de Newton F = ma et Einstein E = mc ² contiennent des informations exceptionnelles et nous permettent d'en déduire tant; les modèles de quarks et de relativité générale sont faciles à décrire, mais ce sont des théories incroyablement profondes qui contrôlent les interactions des particules; des idées telles que la supersymétrie, la théorie de la grande unification et la théorie des cordes étendent les symétries connues de la physique à de nouveaux niveaux. En appliquant de nouvelles techniques mathématiques à l'Univers, nous recherchons une vérité plus profonde dans la réalité que notre niveau actuel de compréhension.

Le modèle original de «l’univers élégant», Mysterium Cosmographicum [le secret de l’univers de Kepler], était symétrique, beau et basé sur des mathématiques qui n’avaient pas été appliquées auparavant. Mais notre récit édifiant sur la façon dont cela s'est avéré être un énorme échec scientifique également.


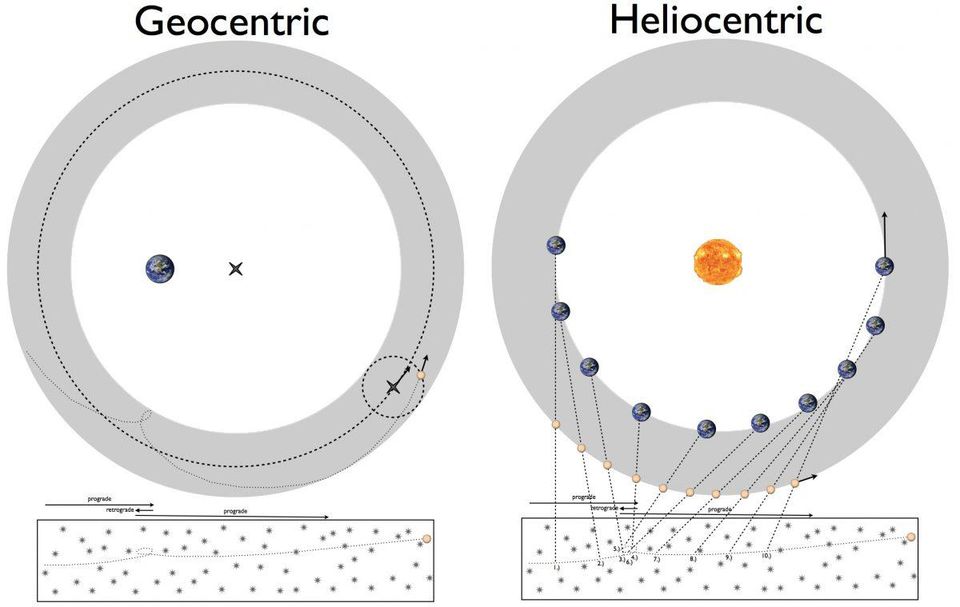L'un des plus grands mystères du XVIe siècle était la façon dont les planètes se déplacent. Cela pourrait être expliqué en utilisant le modèle géocentrique de Ptolémée (à gauche) ou le modèle héliocentrique de Copernic (à droite). Cependant, aucun d'entre eux n'a pu calculer tous les détails avec une précision arbitraire.

Avant Kepler, il y avait trois systèmes principaux décrivant l'Univers [le système solaire en termes de cette époque]:

1. Le modèle de Ptolémée, dans lequel la Terre était immobile, et tout tournait autour d'elle en cercle, utilisait des équivalents , des déférents et des épicycles .
2. Le modèle copernicien, dans lequel le Soleil était immobile et la Terre était l'une des six planètes en orbite autour de lui, utilisait également des épicycles.
3. Le modèle Tycho Brahe, ou géo-héliocentrique , dans lequel le Soleil tournait autour de la Terre, et toutes les autres planètes autour du Soleil en cercles, utilisant également des épicycles.

Kepler, créant des travaux scientifiques des décennies avant Galileo, pensait que les systèmes héliocentriques étaient prometteurs, mais ils avaient besoin de plus que de simples cercles. Leur soutien nécessitait une élégante structure mathématique. Dans un accès de génie, à seulement 24 ans, Kepler a publié une idée qu'il considérait comme la plus belle de ses idées.


Kepler a décidé qu'il devrait y avoir exactement six planètes dans le système solaire avec des orbites précisément définies situées sur des sphères inscrites dans des polyèdres réguliers

Puisque six planètes tournaient autour du Soleil (tout ce qui au-delà de Saturne ne sera découvert que 200 ans plus tard), Kepler a décidé qu'il devrait y avoir six orbites uniques: une pour chacune des planètes. Mais pourquoi six? Pourquoi pas plus, pourquoi pas moins? Pourquoi existe-t-il de telles distances entre eux? La connexion entre les orbites et les mathématiques est devenue son idée d'un univers élégant:

J'ai l'intention de démontrer que Dieu, créant l'univers et plaçant les sphères, avait en tête cinq polyèdres géométriques réguliers et limitait les tailles, les proportions et le mouvement des sphères à leurs tailles.

Vous voyez, en trois dimensions, vous pouvez créer exactement cinq polyèdres à partir de polygones réguliers, ni plus ni moins. Ils ont été découverts par les anciens Grecs il y a 2000 ans, et parfois ils sont appelés polyèdres platoniciens (bien qu'ils aient été découverts bien avant Platon). Kepler a imaginé un système de sphères imbriquées décrit et inscrit autour de chacun des polyèdres, résultant en six orbites sphériques le long desquelles les planètes se déplacent.


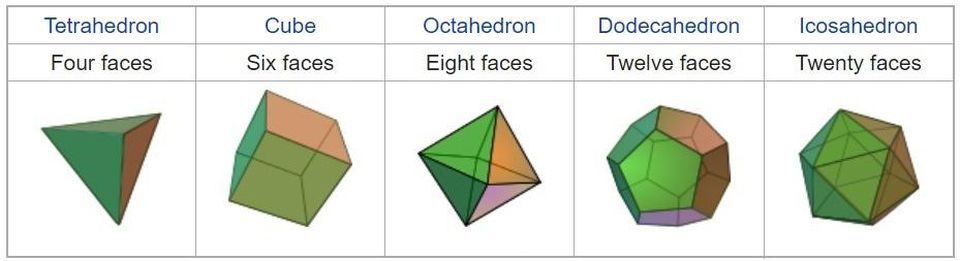Tétraèdre, hexaèdre (cube), octaèdre, dodécaèdre, icosaèdre. Cinq polyèdres réguliers, polygones composés et réguliers

La sphère de Mercure doit être la plus intérieure et est située à l'intérieur de l'octaèdre, un polyèdre régulier, composé de huit triangles équilatéraux. Autour d'elle, la sphère de Vénus est décrite - elle est également inscrite dans l'icosaèdre, une figure à 20 côtés constituée de triangles équilatéraux. Autour d'elle est décrite la sphère de la Terre inscrite dans le dodécaèdre, dont 12 faces sont des pentagones. Autour d'elle est décrite la sphère de Mars inscrite dans un tétraèdre: un polyèdre tétraédrique avec des côtés en forme de triangles équilatéraux. Autour du tétraèdre est décrite la sphère de Jupiter, inscrite dans un cube, le polygone résultant. Et autour d'elle est décrite la dernière sphère, avec l'orbite de Saturne.


Selon la théorie de Kepler, les rayons relatifs des orbites des planètes peuvent être facilement calculés. Cependant, la théorie n'est pas née de l'observation (évidemment la différence entre les sphères de Jupiter et de Mars avec le tétraèdre), et Kepler a dû la rejeter

L'idée de Kepler était en effet brillante; sur cette base, il a été possible de calculer avec précision le rapport des rayons de toutes les orbites. Le problème a été révélé lors de la comparaison des calculs avec les observations. Les rapports des rayons calculés des orbites de Mercure et Vénus, Vénus et la Terre, la Terre et Mars étaient en bon accord avec la réalité, mais les deux derniers mondes ne pouvaient pas rencontrer les rayons prédits par Kepler. En particulier, le modèle a été réfuté par l'orbite de Mars, qui ne correspondait à aucun cercle. Et bien que Kepler ait continué à y travailler, et ait même publié la deuxième édition 20 ans plus tard, sa contribution la plus remarquable était ce que la plupart des scientifiques sont incapables de faire: abandonner son hypothèse bien-aimée.


Les orbites des planètes du système solaire interne ne sont pas entièrement circulaires, mais proches de cela, et la plupart s'écartent du cercle de Mercure et de Mars. De plus, les comètes et les astéroïdes se déplacent le long des ellipses, obéissant au reste des lois de Kepler, si seulement ils sont gravitationnellement liés au Soleil.

Mais ce ne sont pas les sphères imbriquées, mais les ellipses qui ont réussi à prédire correctement le mouvement des planètes. Les trois lois de Kepler , sur le mouvement des planètes le long des ellipses autour du Soleil, sur des zones égales décrites par des rayons à intervalles de temps égaux, et sur l'égalité des rapports des carrés des périodes de révolution des planètes et des cubes des axes semi-majeurs de leurs orbites, ont été réfutées et remplacées par Mysterium Cosmographicum. Le succès des orbites elliptiques a ouvert la voie à la loi de Newton de la gravitation universelle et a engendré l'astrophysique. Malgré l'amour indéfectible de Kepler pour l'idée la plus brillante, l'univers était mieux décrit par un modèle moins élégant. Ayant mis de côté ses espoirs et laissé les données expérimentales se comporter davantage, il a pu réaliser des percées que l'esprit moins doué ne remarquerait pas.


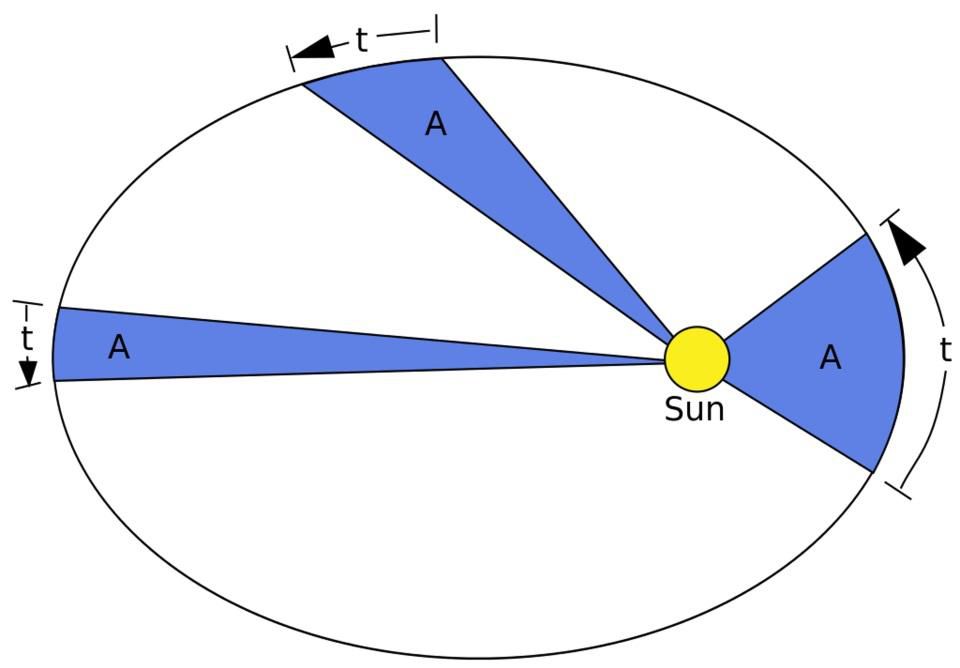Les trois lois de Kepler s'appliquent à tout système gravitationnel ainsi qu'au système solaire.

En physique, on est tenté de succomber au réductionnisme: décrire autant de phénomènes que possible avec le moins de moyens possible. L'idée de l'existence d'une théorie de tout, la seule théorie capable de prédire et de décrire tout ce qui peut être décrit ou prédit dans l'Univers avec la plus grande précision possible, est le rêve et le but ultime de nombreux scientifiques. Cependant, rien ne garantit qu'un tel rêve puisse même se réaliser en principe. Comme l'a écrit le célèbre physicien Lincoln Wulfenstein:

La leçon de Kepler n'est pas que nous devons nous abstenir de soulever des questions apparemment fondamentales; la leçon est que nous ne sommes pas donnés pour savoir s'il existe des réponses simples à ces questions et où elles peuvent être trouvées.

L'élégance, la beauté et le réductionnisme peuvent ouvrir des opportunités incroyables pour des prédictions réussies de nouveaux phénomènes physiques, mais il n'y a aucune garantie que ces prédictions se réaliseront. Faisant une nouvelle percée dans la science fondamentale, de nombreux rêves partagent nos rêves et nos espoirs d'approcher la théorie unificatrice de tout à l'aide de la beauté mathématique et d'une symétrie supplémentaire, mais personne ne les garantit. Puissions-nous tous être aussi ouverts au fait qu'on nous dit les données, comme Kepler l'était, et nous pouvons les suivre, peu importe où ils nous mènent.