Dans notre blog sur Habré, nous avons publié des traductions adaptées de documents du blog The Financial Hacker, consacrés aux questions de création de stratégies de trading en bourse. Plus tôt, nous avons discuté de la
recherche des inefficiences du marché , de la création de
modèles de stratégies de trading et des
principes de leur programmation . Aujourd'hui, nous
nous concentrerons sur l'utilisation d'approches d'apprentissage automatique pour améliorer l'efficacité des systèmes de négociation.
Deep Blue est le premier ordinateur à avoir remporté le Championnat du monde d'échecs. C'était en 1996, et vingt autres années se sont écoulées avant qu'un autre programme, Alpha Go, ne parvienne à vaincre le meilleur joueur de Go. Deep Blue était un système orienté modèle avec des règles d'échecs intégrées. AplhaGo est un système d'exploration de données, un réseau neuronal profond, formé à l'aide de milliers de jeux dans Go. Autrement dit, pour faire un pas des victoires sur les gens qui sont champions d'échecs, pour dominer les meilleurs joueurs de Go, il fallait non pas un morceau de fer amélioré, mais une percée dans le domaine du logiciel.
Dans le présent article, nous envisagerons d'appliquer l'approche d'exploration de données pour créer des stratégies de trading. Cette méthode ne prend pas en compte les mécanismes du marché; elle analyse simplement les courbes de prix et d'autres sources de données pour rechercher des modèles prédictifs. L'apprentissage automatique ou «intelligence artificielle» n'est pas toujours nécessaire pour cela. Au contraire, très souvent, les méthodes d'exploration de données les plus populaires et les plus rentables fonctionnent sans fioritures sous la forme de réseaux de neurones ou de support de méthodes vectorielles.
Principes d'apprentissage automatique
L'algorithme entraîné est alimenté d'échantillons de données, généralement extraites d'une manière ou d'une autre des prix de change historiques. Chaque échantillon se compose de n variables x1 ... xn, qui sont généralement appelées prédicteurs, fonctions, signaux ou, plus simplement, données d'entrée. Ces prédicteurs peuvent être les prix des n dernières barres du graphique des prix ou un ensemble de valeurs d'indicateurs classiques, ou toute autre fonction de la courbe des prix (il y a même des cas où des pixels individuels du graphique des prix sont utilisés comme prédicteurs pour un réseau neuronal!). Chaque échantillon contient également généralement une certaine variable cible y, par exemple, le résultat de la transaction suivante après analyse de l'échantillon ou du prochain mouvement de prix.
Dans la littérature, y est souvent appelé étiquette ou objectif. Dans le processus d'apprentissage, l'algorithme apprend à prédire la cible y sur la base des prédicteurs x1 ... xn. Ce que le système «se souvient» du processus est stocké dans une structure de données appelée modèle spécifique à un algorithme particulier (il est important de ne pas confondre ce concept avec un modèle financier ou une stratégie orientée modèle). Un modèle d'apprentissage automatique peut être des fonctions avec des règles de prédiction écrites à l'aide du code C généré par le processus d'apprentissage. Ou cela pourrait être un ensemble de poids liés au réseau neuronal:
Entraînement: x1 ... xn, y => modèle
Prédiction: x1 ... xn, modèle => y
Les prédicteurs, les fonctions ou tout autre nom que vous souhaitez utiliser doivent contenir des informations suffisantes pour générer des prédictions sur la valeur de la cible y avec une certaine précision. Ils doivent également répondre à deux critères formels. Tout d'abord, toutes les valeurs de prédicteur doivent être dans la même plage, par exemple, -1 ... +1 (pour la plupart des algorithmes sur R) ou -100 ... +100 (pour les algorithmes dans les langages de script Zorro ou TSSB). Donc, avant d'envoyer des données au système, vous devez les normaliser. Deuxièmement, les échantillons doivent être équilibrés, c'est-à-dire répartis uniformément sur les valeurs de la variable cible. Autrement dit, vous devriez avoir le même nombre d'échantillons conduisant à un résultat positif et perdant des ensembles. Si ces deux exigences ne sont pas respectées, de bons résultats ne réussiront pas.
Les algorithmes de régression génèrent des prédictions sur les valeurs numériques, telles que la magnitude ou le signe du prochain mouvement de prix. Les algorithmes de classification prédisent des classes quantitatives d'échantillons, par exemple, si elles précèdent le profit ou la perte de fonds. Certains algorithmes, tels que les réseaux de neurones, les arbres de décision ou les méthodes vectorielles de support, peuvent être exécutés dans les deux modes.
Il existe également des algorithmes qui peuvent apprendre à extraire des échantillons de classe sans avoir besoin d'un y cible. C'est ce qu'on appelle l'apprentissage non supervisé, par opposition à l'apprentissage supervisé. Quelque part entre ces deux méthodes se trouve «l'apprentissage par renforcement», dans lequel le système s'entraîne en exécutant des simulations avec des fonctions spécifiées et utilise le résultat comme objectif. Un adepte d'AlphaGo, un système appelé AlphaZero, a utilisé un apprentissage renforcé, jouant à un million de jeux de Go avec lui-même. En finance, ces systèmes ou produits qui utilisent un apprentissage non supervisé sont extrêmement rares. 99% des systèmes utilisent l'apprentissage supervisé.
Quels que soient les signaux que nous utilisons pour les prédicteurs en finance, dans la plupart des cas, ils contiendront beaucoup de bruit et peu d'informations, et en plus ils seront instables. La prévision financière est donc l'une des tâches les plus difficiles de l'apprentissage automatique. Des algorithmes plus complexes obtiennent ici de meilleurs résultats. La sélection des prédicteurs est essentielle au succès. Pas nécessairement, il devrait y en avoir beaucoup, car cela conduit à un recyclage et à des dysfonctionnements. Par conséquent, les stratégies d'exploration de données utilisent souvent un algorithme présélectionné qui extrait un petit nombre de prédicteurs d'un pool plus large. Une telle sélection préliminaire peut être basée sur la corrélation entre les prédicteurs, leur importance, la richesse de l'information ou simplement le succès / l'échec de l'utilisation de la suite de tests. Des expériences pratiques avec la sélection de cibles peuvent être trouvées, par exemple, sur le blog
Robot Wealth .
Vous trouverez ci-dessous une liste des méthodes d'exploration de données les plus utilisées dans le domaine financier.
1. Soupe d'indicateurs
La plupart des systèmes de négociation ne sont pas basés sur des modèles financiers. Souvent, les traders n'ont besoin que de signaux de trading générés par certains indicateurs techniques, qui sont filtrés par d'autres indicateurs en combinaison avec des indicateurs techniques supplémentaires. Quand il demande à un commerçant comment un tel méli-mélo d'indicateurs peut conduire à une sorte de profit, il répond généralement à quelque chose comme: "Croyez-moi, je troque mes mains et tout fonctionne."
Et c'est vrai. Au moins parfois. Bien que la plupart de ces systèmes ne passeront pas le
test WFA (et certains testent simplement sur des données historiques), un nombre étonnamment élevé de ces systèmes fonctionnent et génèrent des bénéfices. L'auteur du blog Financial Hacker est engagé dans le développement de systèmes de trading personnalisés et raconte l'histoire de l'un des clients qui a systématiquement expérimenté des indicateurs techniques jusqu'à ce qu'il trouve une combinaison qui fonctionne pour certains types d'actifs. Cette méthode d'essai et d'erreur est une approche classique de l'exploration de données, pour réussir, vous n'en avez besoin que de chance et de beaucoup d'argent pour les tests. Par conséquent, vous pouvez parfois compter sur l'obtention d'un système rentable.
2. Modèles de chandelier
À ne pas confondre avec les motifs de bougeoirs qui existent depuis des centaines d'années. L'équivalent moderne de cette approche est le commerce basé sur les mouvements de prix. Vous analysez également les indicateurs d'ouverture, de haut, de bas et de fermeture pour chaque bougie du graphique. Mais maintenant, vous utilisez l'exploration de données pour analyser les bougies de la courbe des prix pour mettre en évidence des modèles qui peuvent être utilisés pour générer des prédictions sur la direction du mouvement des prix à l'avenir.
Il existe des packages logiciels complets à cet effet. Ils recherchent des modèles rentables en termes de critères définis par l'utilisateur et les utilisent pour créer une fonction de détection de modèle. Tout cela peut ressembler à ceci:
int detect(double* sig) { if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6]) return 1; if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6]) return 1; if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; .... return 0; }
Cette fonction C renvoie 1 lorsque le signal correspond à l'un des modèles, sinon elle renvoie 0. Le code long semble indiquer que ce n'est pas le moyen le plus rapide pour rechercher des modèles. Il est préférable d'utiliser une approche dans laquelle la fonction de détection n'a pas besoin d'être exportée, mais peut trier les signaux par leur importance et les trier. Un exemple d'un tel système peut être trouvé
sur le lien .
Le commerce à un prix peut-il fonctionner? Comme dans le cas précédent, cette méthode n'est basée sur aucun modèle financier rationnel. Dans le même temps, tout le monde comprend que certains événements sur le marché peuvent affecter ses participants, ce qui entraîne des schémas prédictifs à court terme. Mais le nombre de ces modèles ne peut pas être important si vous étudiez uniquement la séquence de plusieurs bougies consécutives sur le graphique. Ensuite, vous devrez comparer le résultat avec les données des bougies, qui ne sont pas à proximité, mais, au contraire, sont sélectionnées au hasard sur une période plus longue. Dans ce cas, vous obtiendrez un nombre presque illimité de modèles - et réussirez à vous détacher des concepts de réalité et de rationalité. Il est difficile d'imaginer comment le prix futur peut être prédit sur la base de certaines de ses valeurs la semaine dernière. Malgré cela, de nombreux commerçants travaillent dans ce sens.
3. Régression linéaire
Une base simple pour de nombreux algorithmes complexes d'apprentissage automatique: pour prédire la variable cible y à l'aide d'une combinaison linéaire de prédicteurs x1 ... xn.

Cotes - c'est le modèle. Ils sont calculés pour minimiser la somme des écarts quadratiques entre les valeurs réelles y, les valeurs d'apprentissage et les prévisions y selon la formule:

Pour les échantillons normalement distribués, la minimisation est possible à l'aide d'opérations matricielles, donc les itérations ne sont pas nécessaires. Dans le cas où n = 1 - avec un seul prédicteur x, la formule de régression est réduite à:
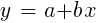
- c'est-à-dire, avant une régression linéaire simple, et lorsque n> 1, la régression linéaire sera multivariante. Une régression linéaire simple est disponible sur la plupart des plateformes de trading, par exemple, l'indicateur
LinReg dans TA-Lib. Lorsque y = prix et x = temps, il peut être utilisé comme alternative aux moyennes mobiles. Dans la plate-forme R, une telle régression est implémentée par la fonction de livraison standard lm (..). Il peut également être représenté par régression polynomiale. Comme dans le cas le plus simple, nous utilisons ici une variable prédictive x, mais aussi son carré et les degrés suivants, donc xn == xn:
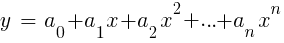
Si n = 2 ou n = 3, la régression polynomiale est souvent utilisée pour prédire le prochain prix moyen à partir des prix lissés des dernières barres. Pour la régression polynomiale, la fonction polyfit du MatLab, R, Zorro et de nombreuses autres plates-formes peut être utilisée.
4. Perceptron
On l'appelle souvent un réseau de neurones avec un seul neurone. En fait, le perceptron est une fonction de régression, comme décrit ci-dessus, mais avec un résultat binaire, à la suite de quoi il est appelé
régression logistique . Bien que, en général, ce ne soit pas une régression, mais un algorithme de classification. Par exemple, la fonction de conseil (PERCEPTRON, ...) du framework Zorro génère du code C qui retourne 100 ou -100 selon que le résultat prévu est seuil ou non:
int predict(double* sig) { if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50) return 100; else return -100; }
Comme vous pouvez le voir, le tableau sig est équivalent aux fonctions xn dans la formule de régression, et les coefficients an sont les facteurs numériques.
5. Réseaux de neurones
La régression linéaire ou logistique ne peut résoudre que des problèmes linéaires. Dans le même temps, les tâches de trading ne rentrent souvent pas dans cette catégorie. Un exemple célèbre est la prédiction de la sortie d'une fonction XOR simple. Cela inclut également la prévision du profit des transactions. Un réseau de neurones artificiels (ANN) peut résoudre des problèmes non linéaires. Il s'agit d'un ensemble de perceptrons qui sont connectés dans un tableau de différents niveaux. Chaque perceptron est un neurone de réseau. Sa sortie devient entrée vers d'autres neurones du niveau suivant:
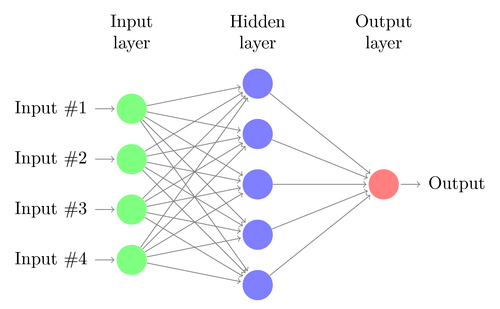
Comme le perceptron, le réseau neuronal est entraîné en déterminant des coefficients qui minimisent l'erreur entre la prédiction et la cible dans l'échantillon. Cela nécessite un processus d'approximation, généralement avec la propagation inverse de l'erreur de la sortie à l'entrée avec l'optimisation des poids en cours de route. Ce processus a deux limites. Premièrement, la sortie des neurones devrait être une fonction différenciable en continu au lieu d'un simple seuil pour le perceptron. Deuxièmement, le réseau ne doit pas être très profond - la présence d'un grand nombre de niveaux cachés de neurones entre les données d'entrée et de sortie ne fait que nuire. Cette deuxième limitation limite la complexité des problèmes qu'un réseau neuronal standard peut résoudre.
Lorsque vous utilisez des réseaux de neurones pour prédire les transactions, vous aurez beaucoup de paramètres qui peuvent être manipulés, ce qui, s'il est mal effectué, peut entraîner un biais de sélection (biais de sélection):
- nombre de niveaux cachés;
- le nombre de neurones dans chaque niveau caché;
- nombre de cycles de rétropropagation - époques;
- degré de formation, largeur de pas de l'époque;
- momentum, facteur d'inertie pour l'adaptation des poids;
- fonction d'activation.
La fonction d'activation émule le seuil du perceptron. Pour la rétropropagation, vous avez besoin d'une fonction constamment différentiable qui génère un pas progressif pour une certaine valeur de x. En règle générale, les fonctions sigmoïde, tanh ou softmax sont utilisées à cet effet. Parfois, une fonction linéaire est utilisée qui renvoie la somme pondérée de toutes les données d'entrée. Dans ce cas, le réseau peut être utilisé pour la régression, la prédiction de valeurs numériques au lieu de la sortie binaire.
Les réseaux de neurones sont inclus dans la livraison standard du package de R (par exemple, nnet est un réseau avec un niveau masqué), ainsi que dans de nombreux autres packages (tels que RSNNS et FCNN4R).
6. Apprentissage profond
Les méthodes d'apprentissage en profondeur utilisent des réseaux de neurones avec de nombreux niveaux cachés et des milliers de neurones qui ne peuvent pas être efficacement formés à l'aide d'une simple rétropropagation. Ces dernières années, plusieurs méthodes sont devenues populaires pour la formation de tels grands réseaux. Ils impliquent généralement une pré-formation de niveaux cachés de neurones pour augmenter l'efficacité de l'apprentissage de base.
La machine Boltzmann restreinte (RBM) est un algorithme de classification non contrôlé avec une structure de réseau spéciale dans laquelle il n'y a pas de connexions entre les neurones cachés. Sparse Auto Encoder (SAE) utilise la structure de réseau habituelle, mais pré-entraîne les couches cachées d'une manière spécifique, reproduisant les signaux d'entrée aux niveaux de sortie avec le moins de connexions actives possible. Ces méthodes vous permettent de mettre en œuvre des réseaux très complexes pour résoudre des problèmes d'apprentissage très complexes. Par exemple, la tâche de vaincre la meilleure personne qui joue au Go.
Les réseaux d'apprentissage en profondeur sont inclus dans les packages deepnet et darch pour R. Deepnet comprend l'auto-encodeur et darch inclut la machine Boltzmann. Voici un exemple de code qui utilise deepnet avec trois niveaux cachés pour traiter les signaux de trading via la fonction neor () du framework Zorro:
library('deepnet', quietly = T) library('caret', quietly = T) # called by Zorro for training neural.train = function(model,XY) { XY <- as.matrix(XY) X <- XY[,-ncol(XY)] # predictors Y <- XY[,ncol(XY)] # target Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1 Models[[model]] <<- sae.dnn.train(X,Y, hidden = c(50,100,50), activationfun = "tanh", learningrate = 0.5, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 100, batchsize = 100, hidden_dropout = 0, visible_dropout = 0) } # called by Zorro for prediction neural.predict = function(model,X) { if(is.vector(X)) X <- t(X) # transpose horizontal vector return(nn.predict(Models[[model]],X)) } # called by Zorro for saving the models neural.save = function(name) { save(Models,file=name) # save trained models } # called by Zorro for initialization neural.init = function() { set.seed(365) Models <<- vector("list") } # quick OOS test for experimenting with the settings Test = function() { neural.init() XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F) splits <- nrow(XY)*0.8 XY.tr <<- head(XY,splits) # training set XY.ts <<- tail(XY,-splits) # test set neural.train(1,XY.tr) X <<- XY.ts[,-ncol(XY.ts)] Y <<- XY.ts[,ncol(XY.ts)] Y.ob <<- ifelse(Y > 0,1,0) Y <<- neural.predict(1,X) Y.pr <<- ifelse(Y > 0.5,1,0) confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }
7. Vecteurs de support
Comme pour les réseaux de neurones, la méthode des vecteurs de support est une autre extension de la régression linéaire. Si vous regardez à nouveau la formule de régression:

On peut alors interpréter les fonctions xn comme les coordonnées d'un espace à n dimensions. Définir la variable cible y sur une valeur fixe déterminera le plan dans cet espace - il sera appelé un hyperplan, car en fait il aura deux tailles (même n-1). L'hyperplan sépare les échantillons avec y> 0 de ceux où y <0. Les coefficients an peuvent être calculés comme le chemin séparant l'avion des échantillons les plus proches - ses vecteurs de support, d'où le nom de l'algorithme. Ainsi, nous obtenons un classificateur binaire avec la séparation optimale des échantillons gagnants et perdants.
Problème: généralement, ces échantillons ne peuvent pas être divisés linéairement - ils sont regroupés au hasard dans un espace de fonction. Il est impossible de tracer un plan lisse entre les options gagnantes et perdantes; si cela pouvait être fait, alors pour son calcul, on pourrait utiliser des méthodes plus simples telles que l'analyse discriminante linéaire. Mais dans le cas général, vous pouvez utiliser l'astuce: ajouter plus de tailles à l'espace. Dans ce cas, l'algorithme de vecteur de support sera capable de générer plus de paramètres avec une fonction nucléaire qui combine deux prédicteurs quelconques - similaire à la transition de la régression simple au polynôme. Plus vous ajoutez de tailles, plus il est facile de diviser les échantillons avec un hyperplan. Il peut ensuite être reconverti dans l'espace à n dimensions d'origine.
Comme les réseaux de neurones, les vecteurs de référence peuvent être utilisés non seulement pour la classification, mais aussi pour la régression. Ils offrent également un certain nombre d'options d'optimisation et de recyclage possible:
- Fonction noyau - le noyau RBF (fonction de base radiale, noyau symétrique) est généralement utilisé, mais d'autres noyaux peuvent être sélectionnés, par exemple sigmoïde, polynomial et linéaire.
- Gamma - largeur de noyau RBF.
- Paramètre de coût C, «pénalité» pour les classifications incorrectes des échantillons d'apprentissage.
La bibliothèque libsvm est souvent utilisée, qui est disponible dans le package e1071 pour R.
8. Algorithme des k voisins les plus proches
Comparé aux lourds ANN et SVM, il s'agit d'un algorithme simple et agréable avec une propriété unique: il n'a pas besoin d'être entraîné. Les échantillons seront le modèle. Cet algorithme peut être utilisé pour un système de trading qui est constamment formé en ajoutant de nouveaux échantillons. Cet algorithme calcule les distances dans l'espace des fonctions de la valeur actuelle aux k échantillons les plus proches. La distance dans l'espace à n dimensions entre les deux ensembles (x1 ... xn) et (y1 ... yn) est calculée par la formule:
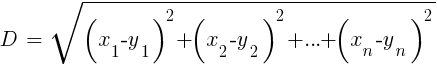
L'algorithme prédit simplement la cible à partir de la moyenne de k variables cibles des échantillons les plus proches, pondérées par leurs distances de retour. Il peut être utilisé à la fois pour la classification et la régression. Pour prédire les voisins les plus proches, vous pouvez appeler la fonction knn dans R ou écrire le code C vous-même à cet effet.
9. K-means
Il s'agit d'un algorithme d'approximation pour une classification non contrôlée. Il est quelque peu similaire à l'algorithme précédent. Pour classer les échantillons, l'algorithme place d'abord k points aléatoires dans l'espace de fonction. Il assigne ensuite à l'un de ces points tous les échantillons avec la plus petite distance. Ensuite, le point se déplace au milieu de ces valeurs les plus proches. Cela génère de nouveaux exemples de liaisons, car certains d'entre eux seront désormais plus proches d'autres points. Le processus est répété jusqu'à ce que le re-référencement résultant du décalage des points s'arrête, c'est-à-dire jusqu'à ce que chaque point soit moyen pour les échantillons les plus proches. Nous avons maintenant k exemples de classes, chacune située à côté d'un k-point.
Cet algorithme simple peut produire des résultats étonnamment bons. Dans R, la fonction kmeans est utilisée pour l'implémenter; un exemple de l'algorithme peut être trouvé
sur le lien .
10. Naive Bayes
Cet algorithme utilise le théorème bayésien pour classer des échantillons de fonctions non numériques (événements), comme les modèles de bougies mentionnés ci-dessus. Supposons que l'événement X (par exemple, le paramètre Open de la barre précédente sous le paramètre Open de la barre actuelle) apparaisse dans 80% des échantillons gagnants. Quelle sera alors la probabilité de gagner l'échantillon en présence de l'événement X? Ce n'est pas 0,8 comme vous pourriez le penser. Cette probabilité est calculée par la formule:
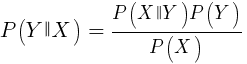
P (Y | X) est la probabilité que l'événement Y (profit) se produise dans tous les échantillons contenant l'événement X (dans notre exemple, Open (1) <Open (0)). Conformément à la formule, elle est égale à la probabilité d'occurrence de l'événement X dans tous les échantillons gagnants (dans notre cas, 0,8), multipliée par la probabilité Y dans tous les échantillons (environ 0,5 si vous suivez les conseils pour équilibrer les échantillons) et divisée par la probabilité d'occurrence de X dans tous les échantillons.
Si nous sommes naïfs et supposons que tous les événements de X sont indépendants les uns des autres, alors nous pouvons calculer la probabilité totale que l'échantillon va gagner en multipliant simplement les probabilités P (X | gagnant) pour chaque événement X. Ensuite, nous arrivons à la formule suivante:
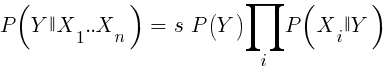
Avec le facteur d'échelle s. Pour qu'une formule fonctionne, les fonctions doivent être choisies de manière à être aussi indépendantes que possible. Ce sera un obstacle à l'utilisation de Bayes naïfs pour le commerce. Par exemple, deux événements Close (1) <Close (0) et Open (1) <Open (0) ne sont probablement pas indépendants l'un de l'autre. Les prédicteurs numériques peuvent être convertis en événements en divisant le nombre en plages distinctes. Naive Bayes est disponible dans le package e1071 pour R.
11. Arbres de décision et de régression
De tels arbres prédisent le résultat de valeurs numériques basées sur une chaîne de décision au format oui / non dans la structure des branches d'arbre. Chaque décision représente la présence ou l'absence d'événements (dans le cas de valeurs non numériques) ou la comparaison de valeurs avec un seuil fixe. Une fonction d'arbre typique, générée, par exemple, par le framework Zorro, ressemble à ceci:
int tree(double* sig) { if(sig[1] <= 12.938) { if(sig[0] <= 0.953) return -70; else { if(sig[2] <= 43) return 25; else { if(sig[3] <= 0.962) return -67; else return 15; } } } else { if(sig[3] <= 0.732) return -71; else { if(sig[1] > 30.61) return 27; else { if(sig[2] > 46) return 80; else return -62; } } } }
Comment un tel arbre est-il obtenu à partir d'un ensemble d'échantillons? Il peut y avoir plusieurs méthodes pour cela, y compris
l'entropie informationnelle de Shannon .
Les arbres de décision peuvent être assez largement utilisés. Par exemple, ils conviennent pour générer des prédictions plus précises que celles qui peuvent être obtenues en utilisant des réseaux de neurones ou des vecteurs de référence. Cependant, ce n'est pas une solution universelle. L'algorithme le plus connu de ce type est C5.0, disponible dans le package C50 pour R.
Pour améliorer encore la qualité des prévisions, vous pouvez utiliser des ensembles d'arbres - ils sont appelés une forêt aléatoire. Cet algorithme est disponible dans des packages R appelés randomForest, ranger et Rborist.
Conclusion
Il existe de nombreuses méthodes d'exploration de données et d'apprentissage automatique. La question critique ici est la suivante: quelles sont les meilleures stratégies, basées sur des modèles ou d'apprentissage automatique? Il ne fait aucun doute que l'apprentissage automatique présente un certain nombre d'avantages. Par exemple, vous n'avez pas besoin de vous soucier de la microstructure du marché, de l'économie, de prendre en compte la philosophie des acteurs du marché ou d'autres choses similaires. Vous pouvez vous concentrer sur les mathématiques pures. L'apprentissage automatique est un moyen beaucoup plus élégant et attrayant de créer des systèmes de trading. De son côté, tous les avantages, sauf un - en plus des histoires sur les forums de traders, le succès de cette méthode dans le trading réel est difficile à suivre.
Presque chaque semaine, de nouveaux articles sont publiés sur le trading à l'aide du machine learning. Ces documents doivent être pris avec beaucoup de scepticisme. Certains auteurs revendiquent des taux de gains fantastiques de 70%, 80%, voire 85%. Cependant, peu de gens disent que vous pouvez perdre de l'argent même si les pronostics sont gagnants. Une précision de 85% se traduit généralement par un indicateur de rentabilité supérieur à 5 - si tout était si simple, alors les créateurs d'un tel système deviendraient déjà milliardaires. Cependant, pour une raison quelconque, reproduire les mêmes résultats simplement en répétant les méthodes décrites dans les articles échoue.
Par rapport aux systèmes basés sur des modèles, il existe très peu de véritables systèmes d'apprentissage automatique réussis. Par exemple, ils sont rarement utilisés par les hedge funds performants. Peut-être qu'à l'avenir, lorsque la puissance de calcul deviendra encore plus accessible, quelque chose changera, mais pour l'instant, les algorithmes d'apprentissage en profondeur restent plus un passe-temps intéressant pour les geeks qu'un véritable outil de gagner de l'argent sur l'échange.
Autres documents financiers et boursiers d' ITI Capital :