Pour vérifier les équations d'Einstein, vous devez frapper un trou noir

Deux équipes de chercheurs ont fait des progrès significatifs pour prouver l'hypothèse de la stabilité du trou noir, le test mathématique le plus important de la théorie générale de la relativité d'Einstein.

En novembre 1915, lors d'une conférence à l'Académie des sciences de Prusse, Albert Einstein a décrit une idée qui a transformé l'humanité autour de l'univers. Au lieu de fixer la géométrie de l'espace et du temps, Einstein a expliqué que nous vivons dans une réalité à quatre dimensions appelée espace-temps, dont la forme fluctue en réponse à la matière et à l'énergie.

Einstein a décrit cette idée importante en détail dans plusieurs équations appelées équations d' Einstein (ou équations du champ gravitationnel) qui forment le noyau de son GTR. Cette théorie a été confirmée par tous les tests expérimentaux auxquels elle a été soumise au siècle suivant.

Et bien que la théorie d'Einstein semble décrire le monde observé, les mathématiques sous-jacentes restent largement mystérieuses. Les mathématiciens ont pu fournir très peu de preuves concernant les équations elles-mêmes. Nous savons qu'ils fonctionnent, mais nous ne pouvons pas dire exactement pourquoi. Même Einstein a dû revenir à des approximations, et non à des solutions exactes, pour voir l'Univers à travers les lentilles qu'il a créées.

Mais au cours de la dernière année, les mathématiciens ont mis l'accent sur les mathématiques GR. Deux groupes ont proposé des solutions liées à un problème important de GR, connu sous le nom d'hypothèse de stabilité du trou noir. Leur travail prouve que les équations d'Einstein correspondent à une intuition physique pour le comportement de l'espace-temps: si vous lui appliquez une perturbation aiguë, elle sursautera comme de la gelée, puis elle se calmera dans un état stable, à partir duquel tout a commencé.

«Si les décisions étaient instables, cela signifierait qu'elles ne sont pas physiques. Ce serait un fantôme mathématique qui existe en mathématiques, mais peu importe du point de vue de la physique », a déclaré Sergiu Kleinerman , mathématicien à l'Université de Princeton, et l'auteur, avec Jeremy Szeftel , d' un des deux résultats .

Pour compléter les preuves, les mathématiciens devaient résoudre la complexité de base des équations d'Einstein. Pour décrire l'évolution de la forme espace-temps, vous avez besoin d'un système de coordonnées - quelque chose comme des lignes de latitude et de longitude - vous indiquant où se trouvent certains points. Et dans l'espace-temps, il est très difficile de trouver un système de coordonnées qui fonctionne partout.

Secouez le trou noir

Comme vous le savez, GR décrit l'espace-temps comme quelque chose comme une feuille de caoutchouc. En l'absence de matière, la feuille est plate. Commencez à y déposer des boules - étoiles et planètes - et la feuille se déformera. Les balles roulent l'une vers l'autre. Lorsque les objets bougent, la forme de la feuille de caoutchouc change également en réponse.

Les équations d'Einstein décrivent l'évolution de la forme espace-temps. Vous leur donnez des informations sur la courbure et l'énergie à chaque point, et ils donnent la forme de l'espace-temps dans le futur. En ce sens, les équations d'Einstein sont similaires à toutes les équations simulant un phénomène physique: ici la balle est au temps zéro, et ici - après cinq secondes.

"Il s'agit d'une version quantitative mathématiquement exacte de l'affirmation selon laquelle l'espace-temps est courbé en présence de matière", a déclaré Peter Hinz, chercheur au Clay Institute of Mathematics de l'Université de Californie à Berkeley, responsable du deuxième résultat avec Andras Vasya.

En 1916, presque immédiatement après la publication de GTR, le physicien allemand Karl Schwarzschild a trouvé une solution exacte aux équations décrivant ce que nous savons maintenant sous le nom de trou noir (ce terme n'est apparu que cinq décennies plus tard ). Plus tard, les physiciens ont trouvé des solutions exactes décrivant un trou noir en rotation et du BH avec une charge électrique.

Et ce sont toutes des décisions exactes décrivant BH. Si vous ajoutez au moins un deuxième BH, l'interaction des forces devient si compliquée pour les mathématiques modernes qu'elle n'y fait face que dans des cas très particuliers.

Cependant, nous pouvons toujours poser des questions importantes sur ce groupe limité de solutions. Une de ces questions a été soulevée en 1952 à la suite des travaux du mathématicien français Yvonne Choquet-Bruhat. En fait, cela ressemble à ceci: que se passe-t-il si vous secouez un trou noir?


Si vous secouez le BH, cela créera des ondes gravitationnelles. Prouver l'hypothèse de stabilité revient à prouver que ces vagues se dispersent dans le vide, comme des vagues à la surface d'un étang après la chute d'une pierre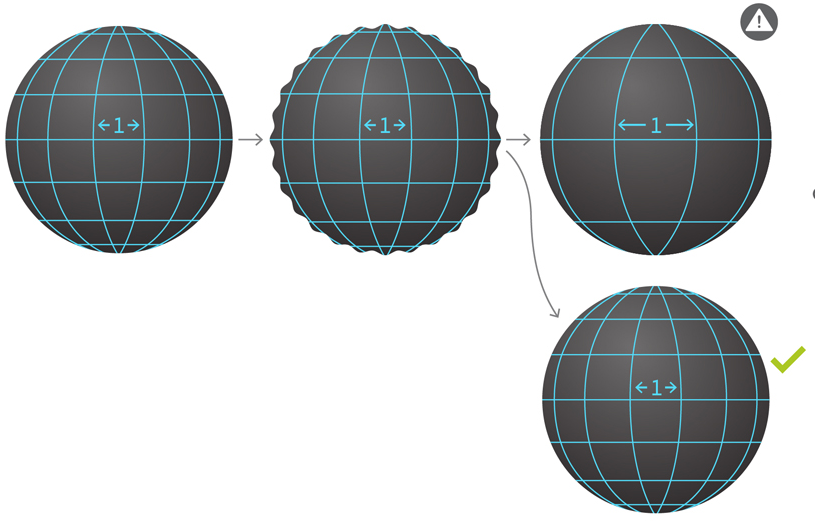


L'espace-temps change avec le temps et la grille utilisée pour mesurer les ondes amorties change avec elle. Le modèle détermine les modifications de la grille et doit être sélectionné correctement. Supposons que nous ayons un espace-temps avec une grille de 1 cm associée à un certain motif. Nous perturberons l'espace-temps pour que des ondes gravitationnelles apparaissent. Un motif incorrectement sélectionné peut entraîner une modification des distances de la grille et il semblerait que les ondes ne s'atténuent pas. Le bon schéma est essentiel pour mesurer le retour à la durabilité.

Ce problème est connu sous le nom d'hypothèse de stabilité BH. Elle prédit que les solutions aux équations d'Einstein seront «stables sous les perturbations». De manière informelle, si vous choquez le BH, l'espace deviendra également plus cher, puis en toge, il se calmera sous une forme qui ressemblera beaucoup à ce que nous avons commencé. «En gros, la durabilité signifie que si nous prenons des solutions spéciales et les scandalisons un peu, modifions les données, la dynamique finale sera très proche de la solution d'origine», a déclaré Kleinerman.

La soi-disant «stabilité» est un test important de toute théorie physique. Pour comprendre cela, il serait utile de présenter un exemple plus familier que BH.

Imaginez un étang. Imaginez maintenant que vous avez révolté sa surface en y jetant une pierre. L'étang est un peu agité, puis il se calmera. Mathématiquement, les solutions des équations utilisées pour décrire l'étang (dans ce cas, les équations de Navier-Stokes ) devraient décrire cette image physique de base. Si la solution originale ne coïncide pas avec la décision dans un avenir lointain, vous pouvez vous interroger sur l'exactitude de vos équations.

"Une équation peut avoir n'importe quelle propriété, elle peut être mathématiquement correcte, mais si elle contredit les attentes physiques, elle ne peut pas être correcte", a déclaré Vasya.


Peter Hinz, mathématicien de l'Université de Californie

Pour les mathématiciens travaillant sur les équations d'Einstein, la preuve de la stabilité était encore plus difficile à trouver que les solutions aux équations elles-mêmes. Prenons le cas d'un espace plat de Minkowski - la plus simple de toutes les configurations spatio-temporelles. Cette solution des équations d'Einstein a été découverte en 1908, dans le contexte de la théorie spéciale antérieure de la relativité d'Einstein. Mais seulement en 1993, les mathématiciens ont pu prouver que si vous secouez l'espace-temps plat et vide, vous obtenez à nouveau l'espace-temps plat et vide. Ce résultat, obtenu par Kleinermann et Demetrios Christodoulou, est un travail vénéré dans ce domaine.

L'une des principales difficultés de la preuve de stabilité est liée au suivi de ce qui se passe dans l'espace-temps à quatre dimensions au cours de l'évolution d'une solution. Vous avez besoin d'un système de coordonnées qui vous permet de mesurer des distances et de déterminer des points dans l'espace-temps, tels que les lignes de latitude et de longitude, utilisés pour déterminer un emplacement sur Terre. Mais il n'est pas facile de trouver un système de coordonnées qui fonctionne à chaque point de l'espace-temps et continue de fonctionner lorsque la forme de l'espace-temps change.

"Nous ne savons pas comment procéder, adapté à tous les cas", a déclaré Hinz dans un e-mail. "L'univers ne nous donne pas de système de coordonnées préféré."

Problème de mesure

La première chose à comprendre sur les systèmes de coordonnées est que les gens les ont inventés. Le second - tous les systèmes de coordonnées ne vous permettent pas de définir tous les points dans l'espace.

Prenez la latitude et la longitude: elles peuvent être attribuées arbitrairement. Les cartographes pouvaient choisir n'importe quelle ligne imaginaire comme premier méridien. Et bien que la latitude et la longitude aident à déterminer presque n'importe quel endroit sur Terre, elles n'ont plus de sens aux pôles nord et sud. Si vous ne saviez rien de la Terre et que vous n'aviez que des relevés de latitude et de longitude sur vos mains, vous pourriez conclure à tort qu'il se passe quelque chose de topologiquement incorrect à ces points.

Cette possibilité - tirer des conclusions incorrectes sur les propriétés de l'espace physique en raison de l'insuffisance du système de coordonnées qui le décrit - est l'essence même de la raison pour laquelle il est si difficile de prouver la stabilité de l'espace-temps.

"Il se peut que la stabilité existe, mais nous utilisons des coordonnées instables, et ainsi ignorer la vérité de la stabilité", a déclaré Michalis Dafermos, mathématicien à l'Université de Cambridge, un spécialiste de premier plan dans l'étude des équations d'Einstein.

Dans le cadre de la théorie de la stabilité d'un trou noir, tout système de coordonnées utilisé devrait évoluer de la même manière que la forme de l'espace-temps - comme un gant confortable s'adapte à changer la forme de la main. La correspondance entre le système de coordonnées et l'espace-temps devrait être bonne au début et rester bonne tout le long. Si ce n'est pas le cas, alors deux choses peuvent se produire qui interfèrent avec les tentatives de prouver l'existence de la stabilité.


Sergiu Kleinerman, mathématicien de l'Université de Princeton

Premièrement, votre système de coordonnées peut ainsi changer de forme, qui se brisera à certains points, tout comme la latitude et la longitude cessent de fonctionner aux pôles. Ces points sont appelés «singularités de coordonnées» (pour les distinguer des singularités physiques, par exemple, les trous noirs). Ce sont des points indéfinis dans le système de coordonnées qui ne permettent pas de décrire complètement le développement de la solution jusqu'au bout.

Deuxièmement, un système de coordonnées mal sélectionné peut masquer le phénomène même physique qu'il doit mesurer. Pour prouver que les solutions des équations d'Einstein arrivent à un état calme après des perturbations, les mathématiciens doivent surveiller attentivement les ondulations de l'espace-temps causées par les perturbations. Pour comprendre pourquoi cela est nécessaire, il convient de revenir à nouveau à l'analogie avec l'étang. Une pierre jetée dans un étang génère des vagues. La stabilité à long terme de l'étang provient du fait que les vagues s'affaiblissent avec le temps - elles deviennent de plus en plus petites, jusqu'à ce qu'il n'y ait aucune trace de leur présence.

La situation est similaire à l'espace-temps. La perturbation provoquera une cascade d'ondes gravitationnelles, et pour prouver la stabilité, il est nécessaire de prouver que ces ondes sont atténuées. Et pour cela, un système de coordonnées, ou «grille», est nécessaire pour mesurer la taille des vagues. La bonne grille permet aux mathématiciens de voir comment les vagues s'aplatissent et finissent par disparaître à jamais.

"L'atténuation doit être mesurée par rapport à quelque chose, et c'est là que le problème de réseau entre en jeu", a déclaré Kleinerman. "Si nous prenons la mauvaise grille, alors même si la stabilité est présente, cela ne peut pas être prouvé, car la grille ne me montrera pas d'atténuation." Et si vous ne calculez pas le taux d'atténuation des ondes, il est impossible de prouver la stabilité. "

Le problème est que bien que le système de coordonnées soit extrêmement important, il n'est pas évident de choisir le système. "Il y a trop de liberté dans le choix des conditions pour cette grille", a déclaré Hinz. "Et la plupart des options se révéleront fausses."

Sur le chemin du but

Une preuve complète de la stabilité des trous noirs nécessite la preuve que toutes les solutions connues des équations d'Einstein pour les BH (avec le spin du trou noir dans certaines limites) sont stables après perturbation. Parmi les solutions bien connues se trouvent la solution de Schwarzschild décrivant l'espace-temps d'un BH non rotatif, et la famille de solutions Kerr décrivant la configuration espace-temps dans laquelle il n'y a qu'un seul BH rotatif (et les propriétés de ce BH - masse et moment angulaire - diffèrent au sein de la famille de solutions) .

Ces deux nouveaux résultats ont partiellement avancé vers la preuve d'une hypothèse complète.

Hinz et Washi, dans un article publié sur arxiv.org en 2016, ont prouvé que les trous noirs à rotation lente sont stables. Mais leur travail ne couvre pas les BH tournant à une vitesse supérieure à un certain seuil.

De plus, leurs preuves ont plusieurs hypothèses sur la nature de l'espace-temps. L'hypothèse originale a eu lieu dans l'espace Minkowski, qui est non seulement plat et vide, mais a également une certaine taille. La preuve de Hintz et Vasya a lieu dans l'espace de Sitter, où l'espace-temps avec accélération se développe vers l'extérieur, comme dans l'Univers réel. Changer la scène simplifie le problème d'un point de vue technique, et cela peut être compris par analogie: si vous jetez une pierre dans un étang en expansion, l'expansion étirera les vagues et elles s'affaibliront plus rapidement que si l'étang ne se dilatait pas.

"Nous regardons un univers avec une expansion accélérée", a déclaré Hinz. «Cela rend la tâche un peu plus facile, car ce processus dilue les ondes gravitationnelles.»

Kleinermann et Scheftel ont une caractéristique légèrement différente. Leur preuve, dont la première partie a été publiée en novembre dernier, se déroule dans l'espace-temps de Schwarzschild - qui est plus proche de l'état original et plus complexe du problème. Ils prouvent la stabilité d'un BH non tournant, mais ne concernent pas les décisions dans lesquelles il tourne. De plus, ils ne prouvent la stabilité de la BH que pour une classe étroite de perturbations - celles dans lesquelles les ondes gravitationnelles générées sont symétriques d'une certaine manière.

Les deux résultats présentent de nouvelles techniques pour sélectionner le système de coordonnées approprié. Hinz et Vasi commencent par une solution approximative d'équations basées sur un système de coordonnées approximatif, et augmentent progressivement la précision de la réponse, jusqu'à ce qu'ils parviennent à des solutions exactes et à des coordonnées qui se comportent bien. Kleinerman et Scheftel utilisent une approche plus géométrique.

Maintenant, les deux équipes tentent de construire une preuve de l'hypothèse complète basée sur leurs méthodes. Certains experts observateurs pensent que le jour où cela fonctionnera n'est pas loin.

"Je crois vraiment que maintenant tout est au stade des difficultés techniques", a déclaré Dafermos. "Il s'avère que pour résoudre ce problème, de nouvelles idées ne sont plus nécessaires." Il a souligné que la preuve finale peut être offerte par n'importe lequel des mathématiciens travaillant actuellement sur le problème.

Pendant cent ans, les équations d'Einstein ont servi d'instruction expérimentale fiable à l'Univers. Maintenant, les mathématiciens sont probablement plus près de démontrer pourquoi ils fonctionnent si bien.