Détermination de la densité de gaz à partir des résultats de la mesure de la pression et de la température avec des capteurs Arduino

Présentation

La tâche de mesurer les paramètres d'un mélange gazeux est répandue dans l'industrie et le commerce. Le problème de l'obtention d'informations fiables lors de la mesure des paramètres de l'état du milieu gazeux et de ses caractéristiques à l'aide de moyens techniques est résolu par les procédures de mesure adoptées dans les normes (MVI), par exemple, lors de la mesure du débit et de la quantité de gaz à l'aide de dispositifs de restriction standard [1], ou à l'aide d'une turbine, débitmètres et compteurs rotatifs et vortex [2].

L'analyse périodique des gaz permet d'établir une correspondance entre le mélange réel analysé et son modèle, selon laquelle les paramètres physicochimiques du gaz sont pris en compte dans le MVI: la composition du mélange gazeux et la densité du gaz dans des conditions standard.
De plus, le MVI prend en compte les caractéristiques thermophysiques du gaz: densité dans les conditions de fonctionnement (pression et température du gaz auquel son débit ou volume est mesuré), viscosité, facteur et facteur de compressibilité.

Les paramètres d'état du gaz mesurés en temps réel comprennent: la pression (pression différentielle), la température, la densité. Pour mesurer ces paramètres, respectivement, des moyens de mesure sont utilisés: manomètres (manomètres différentiels), thermomètres, densitomètres. La mesure de la densité du milieu gazeux peut être mesurée par des méthodes de mesure directes ou indirectes. Les résultats des méthodes de mesure directes et indirectes dépendent de l'erreur des instruments de mesure et de l'erreur méthodologique. Dans des conditions de fonctionnement, les signaux d'information de mesure peuvent être affectés par un bruit important, dont l'écart quadratique moyen peut dépasser l'erreur instrumentale. Dans ce cas, une tâche urgente est le filtrage efficace des signaux d'information de mesure.

Cet article traite de la méthode de mesure indirecte de la densité de gaz dans des conditions de fonctionnement et standard à l'aide d'un filtre de Kalman.

Modèle mathématique pour déterminer la densité de gaz

Passons aux classiques et rappelons l'équation d'état d'un gaz idéal [3]. Nous avons:

1. L'équation de Mendeleev-Clapeyron: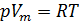

(1)

où:

- pression de gaz;

- volume molaire;

R est la constante de gaz universelle,

;

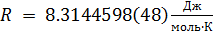
T est la température absolue, T = 273,16 K.

2. Deux paramètres mesurés:

p - pression de gaz, Pa
t est la température du gaz, ° C

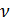
On sait que le volume molaire dépend du volume de gaz V et du nombre de moles de gaz dans ce volume:

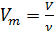
(2)

On sait également que

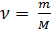
(3)

où: m est la masse de gaz, M est la masse molaire de gaz.

Étant donné (2) et (3) nous réécrivons (1) sous la forme:

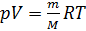
(4).

Comme on le sait, la densité d'une substance

est égal à:

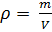
(5).

De (4) et (5), nous dérivons l'équation de la densité de gaz

:

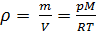
(6)

et introduire la notation du paramètre

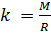
, qui dépend de la masse molaire du mélange gazeux:

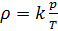
(7).

Si la composition du mélange gazeux ne change pas, alors le paramètre k est constant.
Ainsi, pour calculer la densité du gaz, il est nécessaire de calculer la masse molaire du mélange gazeux.

La masse molaire d'un mélange de substances est définie comme la moyenne arithmétique de la masse molaire des fractions massiques incluses dans le mélange de substances individuelles.

Nous prenons la composition connue des substances dans un mélange gazeux - dans l'air, qui se compose de:

• 23% en poids de molécules d'oxygène
• 76% en poids de molécules d'azote
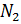
• 1% en poids d'atomes d'argon

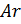
Les masses molaires de ces substances atmosphériques seront respectivement égales à:

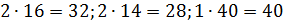
, g / mol.

Nous calculons la masse molaire de l'air comme la moyenne arithmétique pondérée:



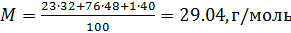
Maintenant, connaissant la valeur de la constante

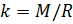
, on peut calculer la densité de l'air selon la formule (7) en tenant compte des valeurs mesurées

et t :

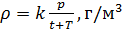
Ramener la densité du gaz à des conditions normales et standard

Dans la pratique, les mesures des propriétés des gaz sont effectuées dans différentes conditions physiques, et pour garantir la comparaison entre différents ensembles de données, des ensembles de conditions standard doivent être établis [4].

Les conditions normalisées de température et de pression sont les conditions physiques établies par la norme, avec lesquelles les propriétés des substances qui dépendent de ces conditions sont corrélées.

Différentes organisations établissent leurs conditions standard, par exemple: l'Union internationale de chimie pure et appliquée (IUPAC), a établi la définition de la température et de la pression standard (STP) dans le domaine de la chimie: température 0 ° C (273,15 K), pression absolue 1 bar (Pa); L'Institut national des normes et de la technologie (NIST) définit une température de 20 ° C (293,15 K) et une pression absolue de 1 atm (101,325 kPa), et cette norme est appelée température et pression normales (NTP); L'Organisation internationale de normalisation (ISO) établit des conditions normalisées pour le gaz naturel (ISO 13443: 1996, confirmée en 2013): température 15,00 ° C et pression absolue 101,325 kPa.

Par conséquent, dans l'industrie et le commerce, il est nécessaire d'indiquer les conditions standard de température et de pression, en fonction desquelles les calculs nécessaires sont effectués.

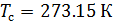
Nous calculons la densité de l'air selon l'équation (8) dans des conditions de fonctionnement de température et de pression. Conformément à (6), nous écrivons l'équation de la densité de l'air dans des conditions standard: température et pression absolue :

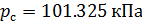
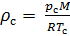
(9).

Nous faisons le calcul de la densité de l'air réduit aux conditions standard. Nous divisons l'équation (9) par l'équation (6) et écrivons cette relation pour :

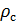
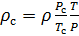
(10).

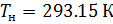
De même, nous obtenons une équation pour calculer la densité de l'air réduit à des conditions normales: température et pression absolue

:

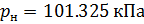
(11).

Dans les équations (10) et (11), nous utilisons les valeurs des paramètres de l'air , T et P de l'équation (8) obtenus dans les conditions de fonctionnement.

La mise en œuvre de la pression et de la température du canal de mesure

Pour résoudre de nombreux problèmes d'obtention d'informations, en fonction de leur complexité, il est pratique de créer un prototype d'un futur système basé sur l'une des plateformes de microcontrôleurs telles que Arduino, Nucleo, Teensy, etc.

Quoi de plus simple? Faisons une plate-forme de microcontrôleur pour résoudre un problème spécifique - créer un système pour mesurer la pression et la température, dépenser moins, éventuellement, des fonds et utiliser tous les avantages du développement logiciel dans l'environnement Arduino Software (IDE).

Pour cela, au niveau matériel, nous aurons besoin de composants:

1. Arduino (Uno, ...) - utiliser comme programmeur;
2. microcontrôleur ATmega328P-PU - microcontrôleur de la future plateforme;
3. un résonateur à quartz de 16 MHz et une paire de condensateurs céramiques de 12-22 pF chacun (selon les recommandations du fabricant);
4. un bouton d'horloge pour réinitialiser le microcontrôleur et un pull-up plus l'alimentation de la broche RESET de la résistance de 1 kOhm du microcontrôleur;
5. BMP180 - transmetteur de température et de pression avec interface I2C;
6. convertisseur d'interface TTL / USB;
7. consommables - fils, soudure, carte de circuits imprimés, etc.

Un schéma de principe de la plateforme, prenant en compte les interfaces nécessaires: une interface série standard, I2C, et rien de plus, est présentée sur la Fig. 1.


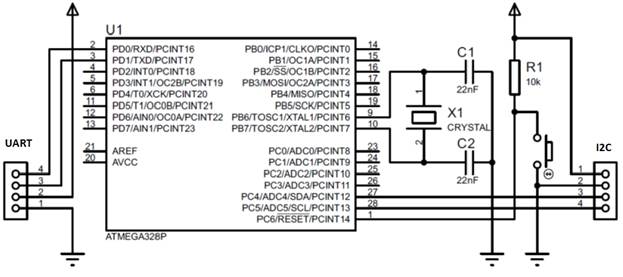Fig. 1 - Schéma de principe d'une plateforme de microcontrôleur pour la mise en œuvre d'un système de mesure de pression et de température

Nous allons maintenant examiner les étapes de la mise en œuvre de notre tâche.

1. Premièrement, nous avons besoin d'un programmeur. Nous connectons Arduino (Uno, ...) à l'ordinateur. Dans l'environnement Arduno Software, dans le menu, allez dans Fichier-> Exemples-> 11. ArdunoISP nous arrivons au programmeur programmeur ArduinoISP, que nous cousons en Arduino. Tout d'abord, dans le menu Outils, sélectionnez respectivement la carte, le processeur, le chargeur, le port. Après avoir téléchargé le programme ArduinoISP sur la carte, notre Arduino se transforme en programmeur et est prêt à l'emploi pour son usage prévu. Pour ce faire, dans l'environnement Arduno Software, dans le menu Outils , sélectionnez l'élément Programmeur: «Arduino as ISP ».

2. Connectez le microcontrôleur esclave ATmega328P via l'interface SPI au programmateur maître Arduino (Uno, ...), Fig. 2. Il convient de noter qu'auparavant, les bits du registre Low Fuse Byte du microcontrôleur ATmega328P étaient définis sur un état non programmé. Accédez à l'environnement Arduno Software et dans le menu Outils , sélectionnez l'élément Burn Loader . Flashage du microcontrôleur ATmega328P.


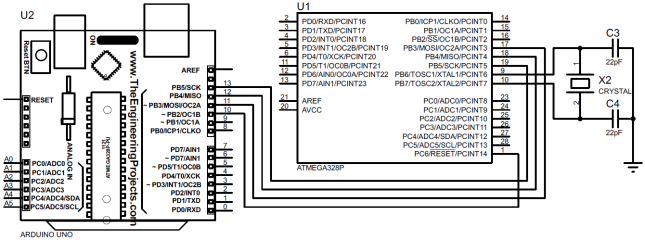Fig. 2 - Schéma de connexion du microcontrôleur au programmateur

3. Une fois le micrologiciel réussi, le microcontrôleur ATmega328P est prêt à être installé sur la plate-forme de microcontrôleur développée (Fig. 3), qui est programmable ainsi que l'Arduino à part entière (Uno, ...). Le programme d'interrogation du transmetteur de pression et de température est indiqué dans le listing 1.


Fig. 3 Système de mesure de pression et de température

Programme Python pour filtrer par canaux de température et de pression, et obtenir des résultats

Le programme Python pour la méthode de détermination de la densité de gaz à partir des mesures de pression et de température est présenté dans le listing 2. Les informations du système de mesure sont affichées en temps réel.


Les résultats des calculs sont présentés par liste et Fig. 4, 5, 6.



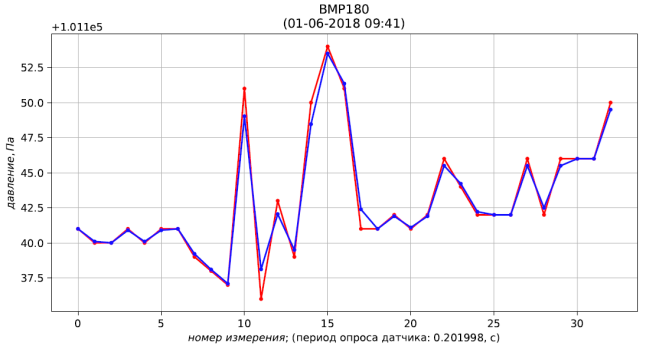Fig. 4 - résultats de mesure (rouge) et de filtration (bleu) de la pression


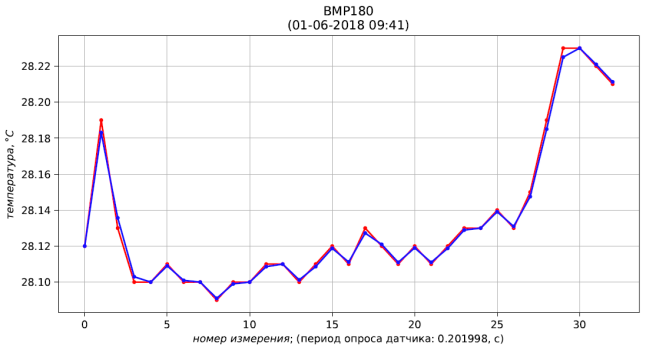Fig. 5 - résultats de mesure (rouge) et filtration (bleu) de la température


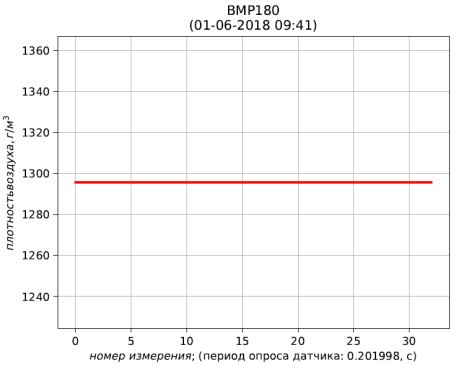Fig. 6 - résultats de calcul de la densité de l'air réduite aux conditions standard (température 273,15 K; pression absolue 101,325 kPa)

Conclusions

Une technique a été développée pour déterminer la densité de gaz à partir de mesures de pression et de température à l'aide de capteurs Arduino et d'un logiciel Python.

Liens vers des sources d'informations

1. GOST 8.586.5-2005. URL
2. GOST R 8.740 - 2011. URL
3. Loi du gaz idéal. URL
4. Conditions standard de température et de pression. URL