Comment les machines analysent le Big Data: une introduction aux algorithmes de clustering

Traduction de la façon dont les machines donnent un sens aux mégadonnées: une introduction aux algorithmes de clustering .

Jetez un oeil à l'image ci-dessous. Il s'agit d'une collection d'insectes (les escargots ne sont pas des insectes, mais nous ne trouverons rien à redire) de différentes formes et tailles. Maintenant, divisez-les en plusieurs groupes selon le degré de similitude. Pas de prise. Commencez par regrouper les araignées.



Terminé? Bien qu'il n'y ait pas de «bonne» solution ici, vous devez avoir divisé ces créatures en quatre groupes . Dans un groupe, il y a des araignées, dans le second - une paire d'escargots, dans le troisième - des papillons et dans le quatrième - un trio d'abeilles et de guêpes.

Bien joué, non? Vous pourriez probablement faire de même s'il y avait deux fois plus d'insectes dans l'image. Et si vous aviez eu beaucoup de temps - ou une envie d'entomologie - alors vous auriez probablement regroupé des centaines d'insectes.

Cependant, pour une machine, le regroupement de dix objets en grappes significatives n'est pas une tâche facile. Grâce à une branche des mathématiques aussi complexe que la combinatoire , nous savons que 10 insectes sont regroupés de 115 975 façons. Et s'il y a 20 insectes, le nombre d'options de regroupement dépassera 50 billions .

Avec une centaine d'insectes, le nombre de solutions possibles sera supérieur au nombre de particules élémentaires dans l'Univers connu . Combien plus? Selon mes estimations, environ cinq cent millions de milliards de milliards de fois plus . Il s'avère que plus de quatre millions de milliards de solutions google ( qu'est-ce que google? ). Et ce n'est que pour des centaines d'objets.

Presque toutes ces combinaisons n'auront aucun sens. Malgré le nombre inimaginable de solutions, vous avez vous-même trouvé très rapidement l'un des rares moyens utiles de clustering.

Nous, les humains, tenons pour acquis notre excellente capacité à cataloguer et à comprendre de grandes quantités de données. Peu importe qu'il s'agisse de texte, d'images à l'écran ou d'une séquence d'objets - les gens, en général, comprennent efficacement les données provenant du monde environnant.

Étant donné qu'un aspect clé du développement de l'IA et de l'apprentissage automatique est que les machines peuvent comprendre rapidement de grands volumes de données d'entrée, comment puis-je améliorer l'efficacité du travail? Dans cet article, nous considérerons trois algorithmes de clustering avec lesquels les machines peuvent rapidement comprendre de grandes quantités de données. Cette liste est loin d'être complète - il existe d'autres algorithmes - mais il est déjà tout à fait possible de commencer par elle.

Pour chaque algorithme, je décrirai quand il peut être utilisé, comment il fonctionne, et je donnerai également un exemple avec une analyse pas à pas. Je crois que pour une réelle compréhension de l'algorithme, vous devez répéter son travail vous-même. Si vous êtes vraiment intéressé , vous vous rendrez compte qu'il est préférable d'exécuter des algorithmes sur papier. Agissez, personne ne vous en voudra!


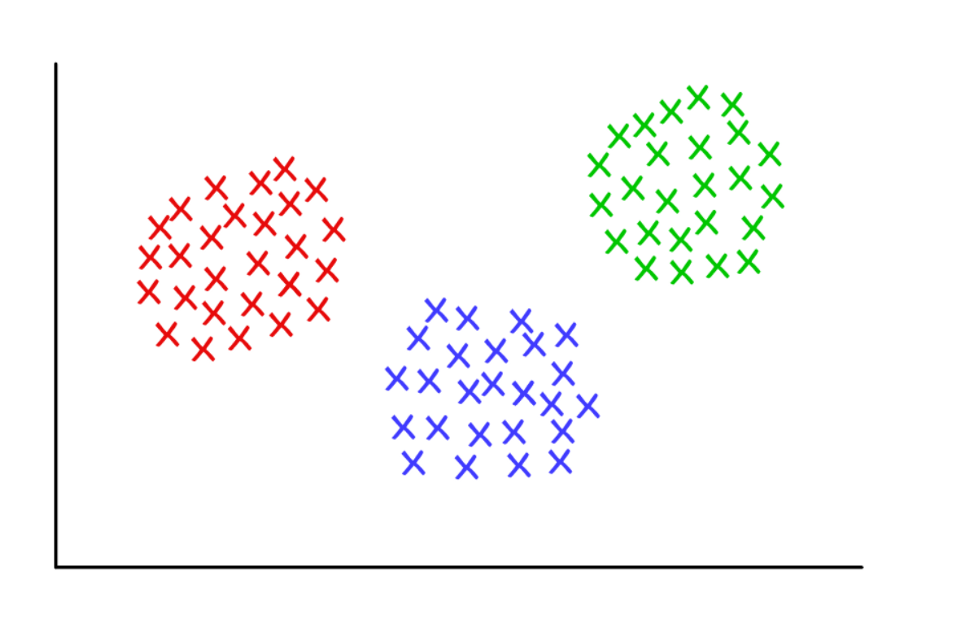Trois grappes étrangement soignées avec k = 3

Clustering K-means

Utilisé par:

Lorsque vous comprenez combien de groupes peuvent être obtenus pour trouver un prédéterminé (a priori).

Comment ça marche:

L'algorithme attribue aléatoirement chaque observation à l'une des k catégories, puis calcule la moyenne pour chaque catégorie. Il réaffecte ensuite chaque observation à la catégorie ayant la moyenne la plus proche, puis calcule à nouveau les moyennes. Le processus est répété jusqu'à ce que des réaffectations soient nécessaires.

Exemple de travail:

Prenez un groupe de 12 joueurs et le nombre de buts marqués par chacun d'eux au cours de la saison en cours (par exemple, entre 3 et 30). Nous divisons les joueurs, disons, en trois groupes.

Étape 1 : vous devez diviser au hasard les joueurs en trois groupes et calculer la moyenne pour chacun d'eux.

Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16 

Étape 2 : réaffectez chaque joueur au groupe avec la moyenne la plus proche. Par exemple, le joueur A (5 buts) va dans le groupe 2 (moyenne = 9). Là encore, nous calculons les moyennes de groupe.

 Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21 

Répétez l' étape 2 encore et encore jusqu'à ce que les joueurs arrêtent de changer de groupe. Dans cet exemple artificiel, cela se produira à la prochaine itération. Arrête ça! Vous avez formé trois clusters à partir d'un ensemble de données!

 Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23 

Les groupes doivent correspondre à la position des joueurs sur le terrain - défenseurs, défenseurs centraux et attaquants. K-means fonctionne dans cet exemple car il y a des raisons de croire que les données seront divisées en ces trois catégories.

Ainsi, sur la base de la variation statistique des performances, la machine peut justifier la localisation des joueurs sur le terrain pour tout sport d'équipe. Ceci est utile pour l'analyse sportive, ainsi que pour toute autre tâche dans laquelle la division de l'ensemble de données en groupes prédéfinis permet de tirer les conclusions appropriées.

Il existe plusieurs variantes de l'algorithme décrit. La formation initiale de clusters peut être effectuée de différentes manières. Nous avons examiné la classification aléatoire des joueurs en groupes, suivie du calcul des moyennes. Par conséquent, les moyennes de groupe initiales sont proches les unes des autres, ce qui augmente la répétabilité.

Une autre approche consiste à former des clusters composés d'un seul joueur, puis à regrouper les joueurs dans les clusters les plus proches. Les grappes résultantes dépendent davantage du stade initial de formation et la répétabilité dans les ensembles de données à forte variabilité diminue. Mais avec cette approche, il peut prendre moins d'itérations pour terminer l'algorithme, car moins de temps sera consacré à la division des groupes.

L'inconvénient évident du clustering k-means est que vous devez deviner à l'avance le nombre de clusters dont vous disposez. Il existe des méthodes pour évaluer la conformité d'un ensemble particulier de clusters. Par exemple, la somme des carrés intra-cluster est une mesure de la variabilité au sein de chaque cluster. Plus les grappes sont «meilleures», plus la somme totale des carrés intracluster est faible.

Regroupement hiérarchique

Utilisé par:

Lorsque vous devez révéler la relation entre les valeurs (observations).

Comment ça marche:

La matrice de distance est calculée dans laquelle la valeur de la cellule ( i, j ) est la métrique de la distance entre les valeurs de i et j . Ensuite, une paire des valeurs les plus proches est prise et la moyenne est calculée. Une nouvelle matrice de distance est créée, les valeurs appariées sont combinées en un seul objet. Ensuite, une paire des valeurs les plus proches est extraite de cette nouvelle matrice et une nouvelle valeur moyenne est calculée. Le cycle se répète jusqu'à ce que toutes les valeurs soient regroupées.

Exemple de travail:

Prenez un ensemble de données extrêmement simplifié avec plusieurs espèces de baleines et de dauphins. Je suis biologiste et je peux vous assurer que beaucoup plus de propriétés sont utilisées pour construire des arbres phylogénétiques . Mais pour notre exemple, nous nous limitons à la longueur caractéristique du corps de six espèces de mammifères marins. Il y aura deux étapes de calcul.



Étape 1 : la matrice des distances entre toutes les vues est calculée. Nous utiliserons la métrique euclidienne qui décrit dans quelle mesure nos données sont éloignées les unes des autres, comme les colonies sur la carte. Vous pouvez obtenir la différence de longueur des corps de chaque paire en lisant la valeur à l'intersection de la colonne et de la ligne correspondantes.



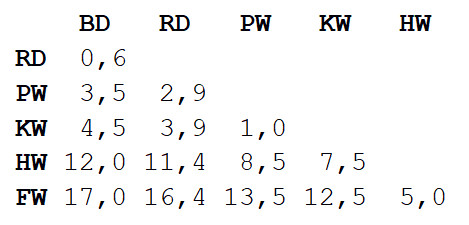Étape 2 : Prenez une paire de deux espèces les plus proches l'une de l'autre. Dans ce cas, il s'agit d'un grand dauphin et d'un dauphin gris, dont la longueur moyenne du corps est de 3,3 m.

Nous répétons l'étape 1, calculant à nouveau la matrice de distance, mais cette fois, nous combinons le dauphin à gros nez et le dauphin gris en un seul objet avec une longueur corporelle de 3,3 m.



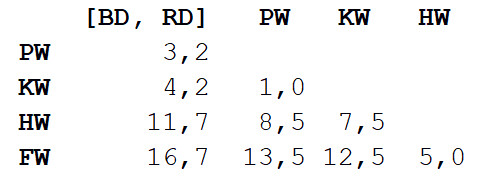
Maintenant, nous répétons l'étape 2, mais avec une nouvelle matrice de distance. Cette fois, la mue et l'épaulard seront les plus proches, alors mettons-les en couple et calculons la moyenne - 7 m.

Ensuite, répétez l'étape 1: encore une fois, calculez la matrice de distance, mais avec la mouture et l'épaulard sous la forme d'un seul objet avec une longueur de corps de 7 m.



Répétez l'étape 2 avec cette matrice. La plus petite distance (3,7 m) sera entre les deux objets combinés, nous allons donc les combiner en un objet encore plus grand et calculer la valeur moyenne - 5,2 m.

Répétez ensuite l'étape 1 et calculez une nouvelle matrice en combinant le gros dauphin / dauphin gris avec la mouture / l'épaulard.



Répétez l'étape 2. La plus petite distance (5 m) sera entre le rorqual à bosse et le nageoire, alors nous les combinons et calculons la moyenne - 17,5 m.

Encore une fois, étape 1: calculez la matrice.



Enfin, répétez l'étape 2 - il ne reste qu'une distance (12,3 m), nous allons donc réunir tout le monde en un seul objet et nous arrêter. Voici ce qui s'est passé:

 [[[BD, RD],[PW, KW]],[HW, FW]] 

L'objet a une structure hiérarchique (rappelez-vous JSON ), il peut donc être affiché sous forme d'arbre graphique ou de dendrogramme. Le résultat est similaire à un arbre généalogique. Plus deux valeurs sont proches sur un arbre, plus elles sont similaires ou plus étroitement liées.


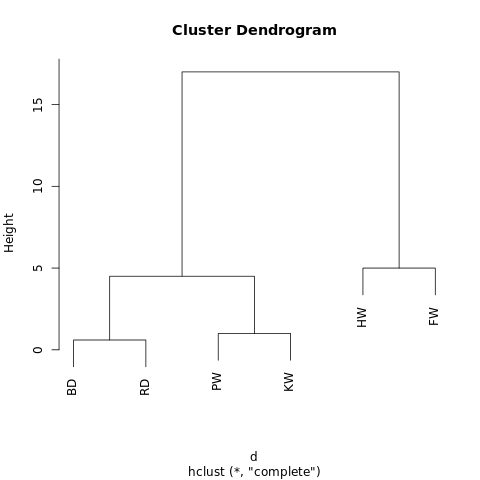Un dendrogramme simple généré à l'aide de R-Fiddle.org

La structure du dendrogramme vous permet de comprendre la structure de l'ensemble de données lui-même. Dans notre exemple, nous avons eu deux branches principales - l'une avec un bossu et un nageoire, l'autre avec un grand dauphin / dauphin gris et une mouture / orque.

En biologie évolutive, des ensembles de données beaucoup plus grands avec de nombreuses espèces et une abondance de caractères sont utilisés pour identifier les relations taxonomiques. En dehors de la biologie, le clustering hiérarchique est appliqué dans les domaines de l'exploration de données et de l'apprentissage automatique.

Cette approche ne nécessite pas de prédiction du nombre requis de clusters. Vous pouvez diviser le dendrogramme résultant en grappes, «couper» l'arbre à la hauteur souhaitée. Vous pouvez choisir la hauteur de différentes manières, en fonction de la résolution souhaitée du clustering de données.
Par exemple, si le dendrogramme ci-dessus est coupé à une hauteur de 10, nous coupons alors les deux branches principales, divisant ainsi le dendrogramme en deux colonnes. S'il est coupé à une hauteur de 2, divisez le dendrogramme en trois groupes.

D'autres algorithmes de clustering hiérarchiques peuvent différer sous trois aspects de ceux décrits dans cet article.

La chose la plus importante est l'approche. Ici, nous avons utilisé la méthode agglomérative : nous avons commencé avec des valeurs individuelles et les avons regroupées cycliquement jusqu'à obtenir un gros cluster. Une approche alternative (et plus complexe sur le plan des calculs) implique la séquence inverse: d'abord un énorme cluster est créé, puis il est séquentiellement divisé en clusters de plus en plus petits jusqu'à ce qu'il reste des valeurs distinctes.

Il existe également plusieurs méthodes de calcul des matrices de distance. Les métriques euclidiennes sont suffisantes pour la plupart des tâches, mais d' autres métriques conviennent mieux dans certaines situations.

Enfin, le critère de liaison peut varier. La relation entre les clusters dépend de leur proximité les uns des autres, mais la définition de la «proximité» peut être différente. Dans notre exemple, nous avons mesuré la distance entre les valeurs moyennes (ou «centroïdes») de chaque groupe et combiné les groupes les plus proches par paires. Mais vous pouvez utiliser une autre définition.

Supposons que chaque cluster se compose de plusieurs valeurs discrètes. La distance entre deux clusters peut être définie comme la distance minimale (ou maximale) entre l'une de leurs valeurs, comme indiqué ci-dessous. Pour différents contextes, il est pratique d'utiliser différentes définitions du critère de jointure.


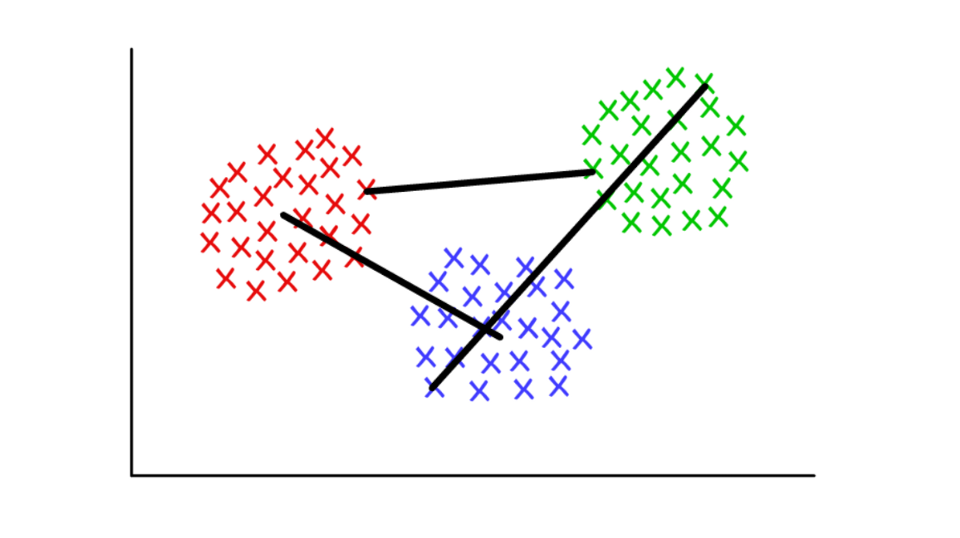Rouge / bleu: pool centroïde; rouge / vert: combinaison basée sur des minima; vert / bleu: fusion basée sur des aigus.

Définition des communautés dans les graphiques (Graph Community Detection)

Utilisé par:

Lorsque vos données peuvent être présentées sous la forme d'un réseau, ou "graphique".

Comment ça marche:

Une communauté dans un graphique peut être grossièrement définie comme un sous-ensemble de sommets qui sont plus connectés les uns aux autres qu'au reste du réseau. Il existe différents algorithmes de définition de communauté basés sur des définitions plus spécifiques, tels que Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector ...

Exemple de travail:

La théorie des graphes est une branche très intéressante des mathématiques qui nous permet de modéliser des systèmes complexes sous la forme d'ensembles abstraits de «points» (sommets, nœuds) reliés par des «lignes» (arêtes).

Peut-être la première application des graphiques qui me vient à l'esprit est l'étude des réseaux sociaux. Dans ce cas, les pics représentent des personnes qui sont reliées par des côtes à des amis / abonnés. Mais vous pouvez imaginer n'importe quel système sous la forme d'un réseau si vous pouvez justifier la méthode de connexion significative des composants. Les applications innovantes du clustering utilisant la théorie des graphes incluent l'extraction de propriétés à partir de données visuelles et l'analyse de réseaux de régulation génétique.

À titre d'exemple simple, regardons le graphique ci-dessous. Cela montre les huit sites que je visite le plus souvent. Les liens entre eux sont basés sur des liens dans des articles Wikipedia. Ces données peuvent être collectées manuellement, mais pour les grands projets, il est beaucoup plus rapide d'écrire un script Python. Par exemple, ceci: https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .


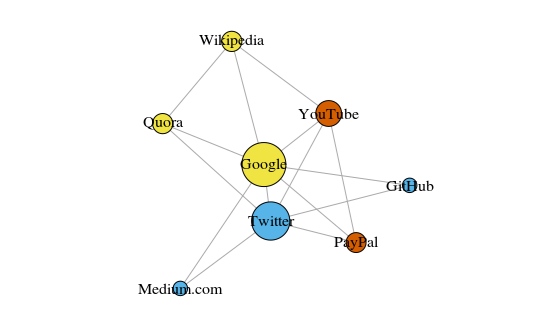Le graphique est construit en utilisant le paquet igraph pour R 3.3.3

La couleur des pics dépend de la participation aux communautés et la taille dépend de la centralité. Veuillez noter que Google et Twitter sont les plus centraux.

De plus, les grappes résultantes reflètent très précisément les tâches réelles (c'est toujours un indicateur important de performance). Les sommets représentant les liens / sites de recherche sont surlignés en jaune; sites surlignés en bleu pour les publications en ligne (articles, tweets ou code); en rouge sont PayPal et YouTube, fondés par d'anciens employés de PayPal. Bonne déduction pour l'ordinateur!

En plus de visualiser de grands systèmes, la véritable puissance des réseaux réside dans l'analyse mathématique. Commençons par convertir l'image réseau en un format mathématique. Ce qui suit est la matrice d' adjacence du réseau.



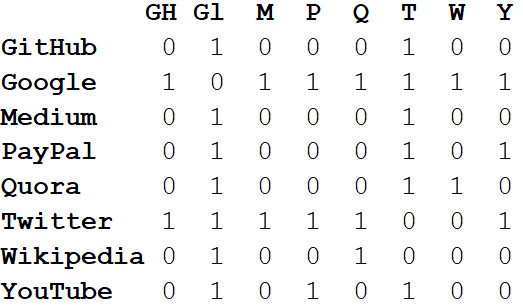
Les valeurs aux intersections des colonnes et des lignes indiquent s'il existe un bord entre cette paire de sommets. Par exemple, entre Medium et Twitter, c'est donc à l'intersection de cette ligne et de la colonne se trouve 1. Et entre Medium et PayPal, il n'y a pas de bord, donc dans la cellule correspondante, il y a 0.

Si nous représentons toutes les propriétés du réseau sous la forme d'une matrice d'adjacence, cela nous permettra de tirer toutes sortes de conclusions utiles. Par exemple, la somme des valeurs de n'importe quelle colonne ou ligne caractérise le degré de chaque sommet, c'est-à-dire le nombre d'objets connectés à ce sommet. Habituellement indiqué par la lettre k .

Si nous additionnons les degrés de tous les sommets et divisons par deux, nous obtenons L - le nombre d'arêtes dans le réseau. Et le nombre de lignes et de colonnes est égal à N - le nombre de sommets dans le réseau.

Connaissant uniquement k, L, N et les valeurs dans toutes les cellules de la matrice d'adjacence A, nous pouvons calculer la modularité de tout clustering.

Supposons que nous ayons regroupé un réseau en plusieurs communautés. Ensuite, vous pouvez utiliser la valeur de modularité pour prédire la «qualité» du clustering. Une modularité plus élevée indique que nous avons divisé le réseau en communautés «exactes» et une modularité plus faible suggère que les clusters sont formés plus par hasard que raisonnablement. Pour plus de clarté:


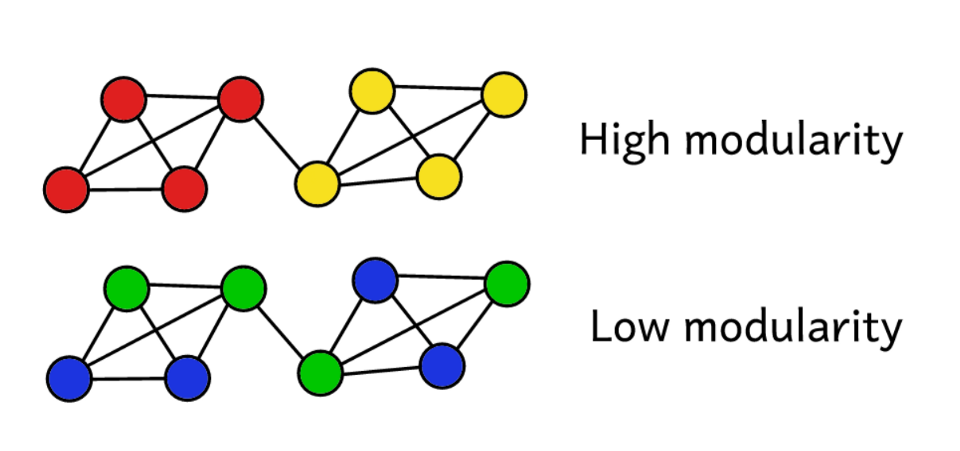
La modularité sert de mesure de la «qualité» des groupes.

La modularité peut être calculée à l'aide de la formule suivante:



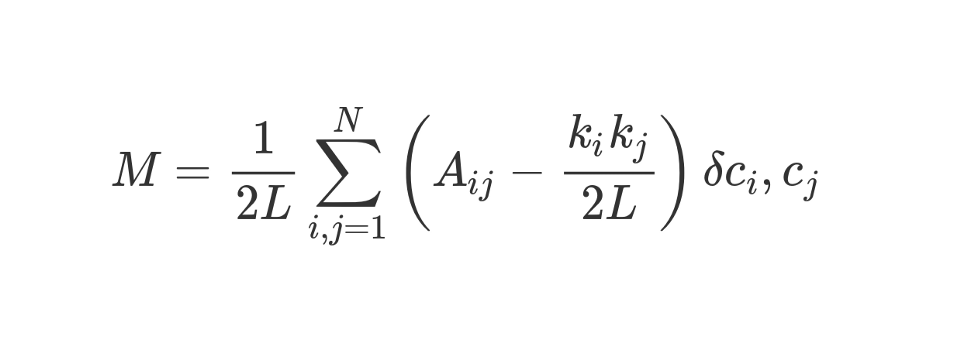
Regardons cette formule à la recherche assez impressionnante.

M , comme vous le savez, c'est la modularité.

Le coefficient 1 / 2L signifie que nous divisons le reste du "corps" de la formule par 2L, c'est-à-dire par le double nombre d'arêtes du réseau. En Python, on pourrait écrire:

 sum = 0 for i in range(1,N): for j in range(1,N): ans = #stuff with i and j as indices sum += ans 

Qu'est-ce que #stuff with i and j ? Le bit entre parenthèses nous dit de soustraire (k_i k_j) / 2L de A_ij, où A_ij est la valeur dans la matrice à l'intersection de la ligne i et de la colonne j.

Les valeurs k_i et k_j sont les degrés de chaque sommet. Ils peuvent être trouvés en additionnant les valeurs de la ligne i et de la colonne j, respectivement. Si nous les multiplions et divisons par 2L, alors nous obtenons le nombre attendu d'arêtes entre les sommets i et j si le réseau était mélangé au hasard.

Le contenu des parenthèses reflète la différence entre la structure réelle du réseau et celle attendue si le réseau était reconstruit au hasard. Si vous jouez avec les valeurs, alors la modularité la plus élevée sera à A_ij = 1 et faible (k_i k_j) / 2L. C'est-à-dire que la modularité augmente s'il y a un bord «inattendu» entre les sommets i et j.

Enfin, nous multiplions le contenu des parenthèses par ce qui est indiqué dans la formule comme δc_i, c_j. Il s'agit de la fonction Kronecker-delta. Voici son implémentation en Python:

 def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A") #returns 1 Kronecker_Delta("A","B") #returns 0 

Oui, si simple. La fonction prend deux arguments, et s'ils sont identiques, elle renvoie 1, sinon, 0.

En d'autres termes, si les sommets i et j tombent dans un cluster, alors δc_i, c_j = 1. Et s'ils sont dans des clusters différents, la fonction renverra 0.

Puisque nous multiplions le contenu des parenthèses par le symbole de Kronecker, le résultat de la somme investie Σ sera le plus élevé lorsque les sommets à l'intérieur d'un cluster sont connectés par un grand nombre d'arêtes «inattendues». Ainsi, la modularité est un indicateur de la façon dont un graphique est regroupé en communautés individuelles.

La division par 2L limite la modularité supérieure à l'unité. Si la modularité est proche de 0 ou négative, cela signifie que le clustering actuel du réseau n'a pas de sens. En augmentant la modularité, nous pouvons trouver un meilleur moyen de regrouper le réseau.

Veuillez noter que pour évaluer la «qualité» du regroupement d'un graphique, nous devons déterminer à l'avance comment il sera regroupé. Malheureusement, à moins que l'échantillon ne soit très petit, en raison de la complexité de calcul, il est tout simplement physiquement impossible de parcourir stupidement toutes les méthodes de clustering d'un graphique en comparant leur modularité.

La combinatoire suggère que pour un réseau à 8 sommets, il existe 4 140 méthodes de regroupement. Pour un réseau à 16 sommets, il y aura déjà plus de 10 milliards de voies, pour un réseau à 32 sommets, 128 septillions, et pour un réseau à 80 sommets, le nombre de méthodes de clustering dépassera le nombre d'atomes dans l'Univers observable .

Par conséquent, au lieu d'énumérer, nous utilisons la méthode heuristique, qui aidera à calculer relativement facilement des clusters avec une modularité maximale. Il s'agit d'un algorithme appelé Fast-Greedy Modularity-Maximization , une sorte d'analogue de l'algorithme de regroupement hiérarchique aggloméré décrit ci-dessus. Au lieu de se combiner sur la base de la proximité, Mod-Max unit les communautés en fonction des changements de modularité. Comment ça marche:

Tout d'abord, chaque sommet est affecté à sa propre communauté et la modularité de l'ensemble du réseau est calculée - M.

Etape 1 : pour chaque paire de communautés connectées par au moins un front, l'algorithme calcule le changement résultant de la modularité ΔM dans le cas de la combinaison de ces paires de communautés.

Étape 2 : alors une paire est prise, lorsqu'elle est combinée, ΔM sera maximale et combinée. Pour ce clustering, une nouvelle modularité est calculée et stockée.

Les étapes 1 et 2 sont répétées : chaque fois qu'une paire de communautés se joint, ce qui donne le plus grand ΔM, un nouveau schéma de clustering et son M.

Les itérations s'arrêtent lorsque tous les sommets sont regroupés en un énorme cluster. Maintenant, l'algorithme vérifie les enregistrements stockés et trouve le schéma de clustering avec la modularité la plus élevée. C'est elle qui revient en tant que structure communautaire.

C'était difficile à calculer, du moins pour les gens. La théorie des graphes est une riche source de problèmes de calcul difficiles et de problèmes NP-difficiles. À l'aide de graphiques, nous pouvons tirer de nombreuses conclusions utiles sur les systèmes et ensembles de données complexes. Demandez à Larry Page, dont l'algorithme PageRank - qui a aidé Google à passer d'une startup à une dominante mondiale en moins d'une génération - est entièrement basé sur la théorie des graphes.

Les études sur la théorie des graphes se concentrent aujourd'hui sur l'identification des communautés. Il existe de nombreuses alternatives à l'algorithme Modularity-Maximization, qui, bien qu'utile, n'est pas sans inconvénients.

Premièrement, avec une approche agglomérative, de petites communautés bien définies sont souvent combinées en de plus grandes. C'est ce qu'on appelle une limite de résolution - l'algorithme n'alloue pas les communautés plus petites qu'une certaine taille. Un autre inconvénient est qu'au lieu d'un pic global prononcé et facilement réalisable, l'algorithme Mod-Max cherche à générer un large "plateau" à partir de nombreuses valeurs de modularité proches. Par conséquent, il est difficile d'identifier le gagnant.

D'autres algorithmes utilisent différentes méthodes pour définir les communautés. Par exemple, Edge-Betweenness est un algorithme de division (division) qui commence par regrouper tous les sommets en un seul cluster énorme. Ensuite, les arêtes les moins «importantes» sont supprimées de manière itérative jusqu'à ce que tous les sommets soient isolés. Le résultat est une structure hiérarchique dans laquelle les sommets sont plus proches les uns des autres, plus ils sont similaires.

L'algorithme, Clique Percolation, prend en compte les intersections possibles entre les communautés. Il existe un groupe d'algorithmes basés sur une marche aléatoire sur un graphique, et il existe des méthodes de regroupement spectral qui traitent de la décomposition spectrale (composition par eigende) de la matrice d'adjacence et d'autres matrices qui en dérivent. Toutes ces idées sont utilisées pour mettre en évidence des fonctionnalités, par exemple, en vision industrielle.

Nous n'analyserons pas en détail des exemples de travail pour chaque algorithme. , , 20 .

Conclusion

, - , , . , , 20-40 .

, — , . , , .

, , , , . , - , , ? - !