Un article sur l'analyse du jeu par un réseau commercial bien connu a suscité un
grand intérêt pour
Cloud4Y . Voici quelques passages pour vous mettre au courant:
Une fois, par un matin de printemps ensoleillé, en lisant un forum de la ville, je suis tombé sur un lien avec un jeu simple d'un réseau commercial bien connu. Le jeu (action) dédié à la Coupe du monde était un terrain simple de trois par trois rempli de ballons de football. En cliquant sur le ballon, nous avons ouvert une image avec un produit particulier. Lors de l'ouverture de trois images identiques, le participant s'est vu garantir une réception gratuite de ce produit dans l'un des magasins du réseau. En outre, sous l'une des balles, il y avait une image d'un carton rouge, dont l'ouverture signifiait la fin de la partie.
L'auteur de l'article a commencé à enquêter sur les raisons de sa perte et, sur la base des résultats des calculs, a découvert ce qui suit:
Un rapide croquis des formules sur une serviette, et il s'est avéré que la probabilité de gagner est de 1/4. Pour 5 champs, j'ai dû bricoler, mais la probabilité calculée était également de 25%.
...
En exécutant le script, j'ai obtenu un résultat inattendu - 25% des gains. Ayant joué avec le nombre d'éléments gagnants et le nombre total de champs, j'ai découvert que la probabilité de gagner dans un tel jeu ne dépend pas du nombre de champs et est égale à un divisé par le nombre d'éléments gagnants augmenté d'une unité.
Nous nous sommes intéressés à l'exactitude d'un tel calcul et, en remplaçant la serviette par Excel, nous nous sommes mis au travail à la recherche de la vérité mathématique. Les lecteurs qui aiment la théorie des probabilités sont invités à chatter, afin de vérifier l'exactitude de nos calculs.
Tout d'abord, nous découvrons les règles du jeu. En cela, sans le savoir, l'utilisateur de Habr
Stecenko a aidé dans son
commentaire . Il écrit également:
Si vous regardez le script de l'auteur, il est écrit en supposant qu'il DOIT y avoir trois cartes d'un produit sur le terrain, une carte de cinq autres biens et un carton rouge, tandis que la description du jeu ne suit absolument pas cela - les règles ne disent pas que la combinaison gagnante doit être présente sur le terrain.
Cependant, les règles prévoient un total de 26 produits. Il s'avère que l'émission de 9 cartes est générée: 8 cartes sont des combinaisons de 26 produits avec répétitions, et une carte est rouge.
Dans de telles conditions, le calcul de la probabilité mathématique de gagner est un peu plus compliqué que l'auteur du post original ne l'a suggéré. Le jeu se compose de plusieurs couches:- La probabilité d'ouvrir N cartes sans ouvrir la rouge est la probabilité d'une durée différente du jeu, qu'il y ait ou non un prix.
- La probabilité de collecter une combinaison de 3 cartes avec les mêmes biens. Cette probabilité varie avec différentes durées de jeu. Il est important de comprendre qu'un ensemble de 8 cartes avec des marchandises et toujours une rouge ne contient pas nécessairement au moins une paire de cartes identiques, sans parler de trois à la fois.
Commençons par un simple - comprendre comment le nombre de participants diminuera avec l'augmentation du nombre de cartes qu'ils ouvrent en raison de la règle du carton rouge.
Chances de longueurs de jeu différentes
Nous calculons la probabilité que pour N essais (cartes ouvertes) le rouge soit ouvert.UPD: Initialement, nous avons calculé la probabilité d'ouverture rouge en utilisant une distribution binomiale. Cela ne nous garantissait pas strictement 1 carton rouge, avec une telle distribution, il y avait très probablement un carton rouge, mais il pouvait y avoir 0 ou tous les 9 avec une très, très petite probabilité. Encore une fois, merci à Stecenko pour avoir signalé une erreur dans le commentaire et suggéré la bonne solution .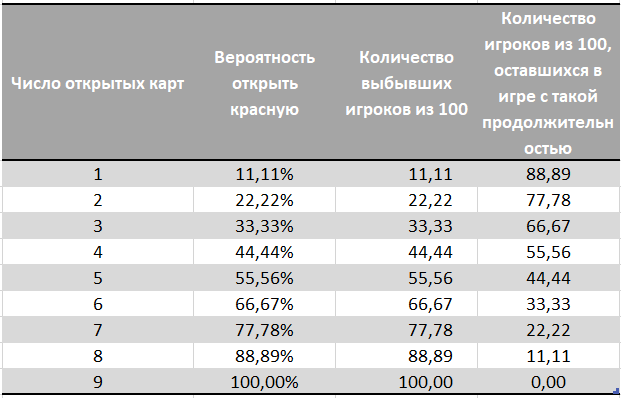
La dernière colonne montre combien de joueurs sur cent restent dans le jeu avec cette durée. Les autres joueurs sont éliminés à cause du carton rouge, sans savoir s'il y avait une combinaison gagnante dans le jeu de cartes émis.
Nous allons maintenant calculer les probabilités de collecter une combinaison de trois cartes avec les mêmes marchandises. C'est une condition pour recevoir un prix.
Chances de prix
Nous décomposons le jeu logiquement. Nous ouvrons la première carte, puis sélectionnons la paire pour cette carte, sélectionnons les trois pour la paire. Avec cette approche, nous pouvons calculer la probabilité d'obtenir 3 cartes identiques en trois tentatives ou plus, en se basant sur le fait qu'il y a 26 produits dans le jeu.
Pour les tâches avec un nombre fixe de tests ou de tests, si le résultat d'un test ne peut être qu'un succès ou un échec, les tests sont indépendants et la probabilité de succès reste constante tout au long de l'expérience, nous utiliserons la formule de Bernoulli - dans Excel, la fonction BINOM.DIS.
En utilisant la fonction BINOM.RASP, vous pouvez calculer, par exemple, la probabilité que deux des trois prochains nouveau-nés soient des garçons. Quelle est la probabilité d'en découvrir trois identiques en trois tentatives?
= BINOM.RASP (3; 3; 1/26; 0) par masque
= BINOM.DISP (nombre de succès; nombre d'essais; probabilité de succès; intégrale)
Ou voici la formule pour calculer la probabilité d'obtenir 3
biens identiques et certains en 8 tentatives.
= BINOM.RASP (3; 8; 1/26; 0), non?
Pas vraiment. Lorsque nous avons atteint la durée du jeu en 4 essais, ne permettant pas l'ouverture du rouge et continuant à jouer, nous obtenons une situation avec la possibilité de deux paires pour sélectionner un gagnant trois.
Classiquement, deux produits sur 26 sont A et B. Nos cartes ouvertes sont A-B-A-B. La probabilité n'est plus 1/26, mais 1/26
+ (1/26) * "La probabilité de deux paires pour une durée donnée du jeu .
"La probabilité de deux paires pour une durée donnée du jeu = BINOM.DISP (2; 5; 1/26; 0) ^ 2
Lorsque vous atteignez un jeu plus long à la 7e tentative, nous obtenons des combinaisons comme A-B-A-B-B-B. Cela signifie que la probabilité est désormais égale
= 1/26 * (1 + BINOM.RASP (2; 7; 1/26; 0) ^ 2 + BINOM.RASP (2; 7; 1/26; 0) ^ 3) et nous recherchons une troisième carte pour 1, 2 ou trois paires.
UPD: De plus, initialement, nous n'avons pas pris en compte que la première tentative dans notre calcul des gains, débarrassée de la probabilité de choisir le rouge, est la découverte de l'un des 26 produits, ce qui signifie 100% de succès. Le nombre de répétitions d'un produit dans la matrice est le nombre de correspondances avec un même produit, ce qui signifie que deux répétitions pour un seul produit suffisent pour gagner, et non pas 3 avec un résultat prédit spécifique. Ainsi, le premier choix de n'importe quelle carte et deux tentatives de ramasser deux autres de la même forme forment un total de trois expériences.Connaissant les probabilités, nous construisons une matrice:
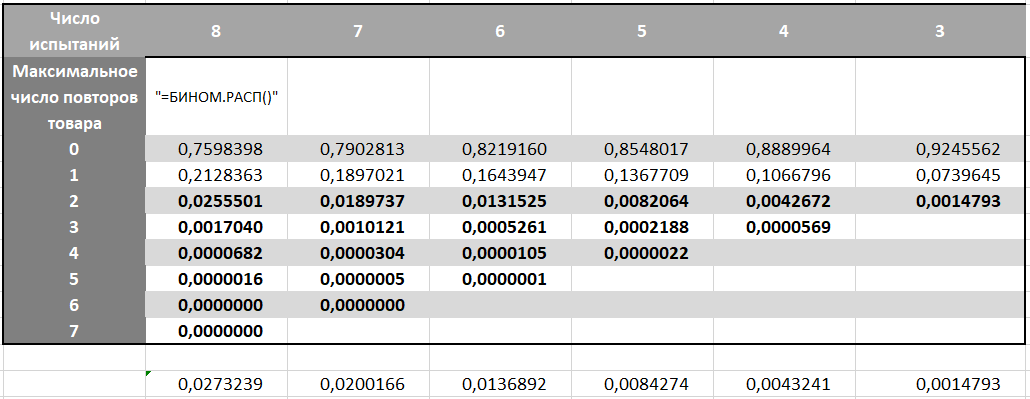
On y retrouve la probabilité de chaque nombre maximum de répétitions d'un produit pour chaque variante de la durée du jeu. Rappelez-vous que la probabilité de gagner change à la 4e tentative et à 7, ce qui signifie que nous en tenons compte dans la formule BINOM.RASP
Nous avons besoin d'options avec un nombre maximum de répétitions de tout produit de 3 ou plus. Puisque le jeu s'arrête dès que nous collectons les trois, nous ajoutons les probabilités par colonnes dans la zone en gras.
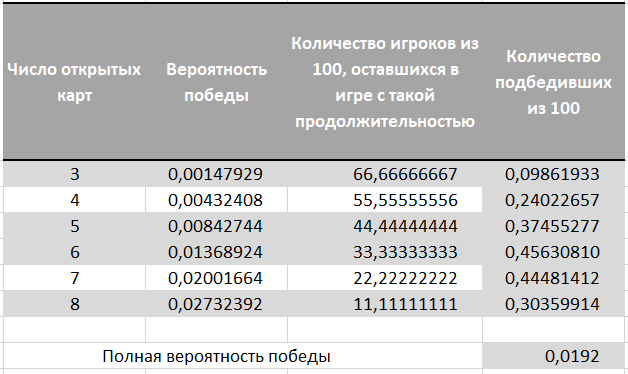
Ensuite, nous multiplions les chances de chaque durée de jeu par les chances de gagner un prix avec une telle durée. En résumant ces pièces, nous obtenons une probabilité de 0,0192 ou 192 gagnants pour 10 000 joueurs.
Oui, en effet, c'est une très faible probabilité. Pas du tout 25%. Regardons à nouveau les règles du jeu:
8. Fonds du prix:
8.1. Prix disponibles: noms et quantités
...
Total 166 000
Nous divisons 116 000 par la probabilité de gagner et obtenons environ 6 millions de participants afin de jouer tous les prix. Rappelons qu'au 1er janvier 2018, selon Rosstat, il y avait 146 938 921 résidents permanents en Russie. Apparemment, c'est l'idée des organisateurs du jeu - donner une chance de gagner presque tous les citoyens de la Russie.UPD: La probabilité finale a changé après les changements. Nous pouvons maintenant tester nos calculs dans la pratique à l'aide de scripts, mais le don de l'esprit de Dieu des mathématiciens et théoriciens des générations précédentes est incroyable, qui a calculé un tel nombre de probabilités, trouvant la bonne solution sur papier et utilisant des expériences mentales.L'analyse du code a montré à l'auteur de la publication originale que même avant le début du jeu, le script "connaissait" son résultat, mais personne ne savait quel résultat prédéterminé le script donnerait à un utilisateur spécifique. Connaissant le côté mathématique du problème, vous pourrez tirer votre propre conclusion sur l'honnêteté des organisateurs.