Logique floue à contrôler
Le texte est basé sur des matériaux du livre de V. Gostev. "Régulateurs flous dans les systèmes de modélisation automatique." Comme toutes les publications sérieuses sur le sujet, ce livre est surchargé de calculs mathématiques et difficile pour le lecteur non préparé. Pendant ce temps, les principes de création et d'utilisation de la logique floue en eux-mêmes sont assez simples et clairs. Ce texte est une tentative de traduire un exemple d'un livre d'un langage mathématique à un langage technique.
Une séquence possible de conception d'un contrôleur basé sur une logique floue est illustrée en compliquant séquentiellement les règles logiques et en sélectionnant les paramètres à l'aide de méthodes d'optimisation.
Énoncé du problème
Considérons la synthèse d'un contrôleur PID numérique et d'un contrôleur flou pour un système de contrôle de missiles par angle d'attaque. En utilisant la modélisation mathématique, nous déterminons les processus dans le système et donnons une évaluation comparative de la qualité du système en utilisant des contrôleurs synthétisés.
Prendre l'angle d'attaque comme coordonnée de sortie du missile:  et pour la coordonnée d'entrée l'angle de braquage
et pour la coordonnée d'entrée l'angle de braquage  définir la fonction de transfert de la fusée sous la forme:
définir la fonction de transfert de la fusée sous la forme:
 où:
où:
 - coefficient de conversion de la fusée,
- coefficient de conversion de la fusée,
 - coefficient d'amortissement,
- coefficient d'amortissement,
 - constante de temps.
- constante de temps.
Ci-après, la «fonction de transfert» n'est pas utilisée dans une définition classique stricte, comme le rapport des transformations de Laplace.
Dans l'étude du système de contrôle, nous supposons que la dépendance des paramètres de la fusée sur le temps de vol est définie comme

Pour simplifier les calculs, nous décrivons le mécanisme de direction par la fonction de transfert de la liaison d'intégration  Dans ce cas, l'entrée système
Dans ce cas, l'entrée système  - angle d'attaque donné, sortie du système
- angle d'attaque donné, sortie du système  Est l'angle d'attaque établi par la fusée, m (t) est le signal de commande à la sortie du contrôleur, et l'objet de commande est décrit par la fonction de transfert générale:
Est l'angle d'attaque établi par la fusée, m (t) est le signal de commande à la sortie du contrôleur, et l'objet de commande est décrit par la fonction de transfert générale:

(L'appareil à gouverner analogique et la fusée sont inclus dans l'objet de commande).
La loi de variation de l'action d'entrée est donnée par le polynôme:

Il est nécessaire de développer un contrôleur qui assure le développement de l'effet d'entrée à l'aide d'un contrôleur PID et d'un contrôleur basé sur une logique floue.
Pour sélectionner les coefficients des régulateurs.
Comparez le transitoire avec le contrôleur PID et le contrôleur basé sur la logique floue.
Modèle d'objet dynamique
Créez un modèle dynamique dans un environnement de modélisation structurelle.
Le circuit modèle lui-même est illustré à la figure 1.
L'action spécifiée est définie sous la forme d'un bloc constant, une variable du script est définie comme paramètres. Les paramètres de la fonction de transition sont définis sous forme de variables.
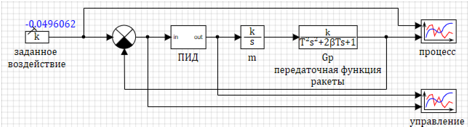 Figure 1. Schéma d'un modèle dynamique d'une fusée.
Figure 1. Schéma d'un modèle dynamique d'une fusée.Réglage du régulateur
Le bloc PID est un sous-modèle (Fig. 2), qui utilise le bloc standard «Contrôleur PID discret». La fréquence d'échantillonnage est sélectionnée égale à 0,001 s.
 Figure 2. Contrôleur PID avec circuit de réglage.
Figure 2. Contrôleur PID avec circuit de réglage.Les paramètres du contrôleur sont définis sous la forme de noms de signaux globaux du projet
Kp, Ki, Kd. Cela vous permet de modifier les paramètres pendant la simulation et d'ajuster le régulateur.
Le bloc
«Optimisation» a été utilisé pour régler le régulateur, le critère d'optimisation est l'écart type minimum.
L'unité d'optimisation effectue l'optimisation tout au long du processus de transition. Le résultat de l'optimisation est un vecteur de trois coefficients, qui est envoyé au bloc "Ecrire dans la liste des signaux", où les valeurs calculées sont transférées aux signaux et, en conséquence, les valeurs des coefficients PID changent. Pour configurer le contrôleur, nous définissons les paramètres d'optimisation suivants:
Valeurs initiales de tous les coefficients
1.La plage de sélection est réglée de
-50 à
+50Précision de sélection
0,001Écart type maximal après optimisation
0,01Dans ce cas, l'unité d'optimisation a calculé les valeurs optimales suivantes des coefficients:
Kp = -1,7498597; Ki = 17,891995; Kd = 11,606602 .
Avec ces coefficients, l'écart type dans le transitoire donné était de
0,008738090
Figure 3. Transitoire.
| 
Figure 4. Gestion. |
Contrôleur à logique floue
Les principaux avantages d'un contrôleur basé sur une logique floue sont la simplicité et la clarté de la formation des règles de contrôle de l'objet.
Par exemple, dans le livre "Fuzzy Regulators in Automatic Modeling Systems", les règles de régulation floue pour contrôler la fusée par l'angle d'attaque sont décrites sous la forme d'une expression mathématique:

où

- erreur système, erreurs de changement de vitesse (dérivée première), erreurs d'accélération (dérivée seconde);
m - contrôle l'action sur l'objet;

- estimations linguistiques de l'erreur, taux de variation de l'erreur (première dérivée) de l'erreur et deuxième dérivée de l'erreur, considérées comme des ensembles flous définis sur un ensemble universel

;

- estimations linguistiques de l'action de contrôle sur l'objet, sélectionnées parmi les ensembles de termes de la variable
mLe lecteur peut demander: comment ça va, ta mère, je suis désolée, tu comprends?
Parfois, je doute que les mathématiciens eux-mêmes comprennent ce qu'ils ont écrit. Derrière les virages mathématiques abstrus, se cache le grand secret des règles de régulation floue. Le voici:
réduire beaucoup
norme - ne pas toucher
petit - augmenterSi vous traduisez de la langue mathématique de l'oiseau en russe, alors l'expression

signifie littéralement ce qui suit:
Si elle est
supérieure à la normale et que l'
écart augmente et que
le taux de croissance augmente , alors nous
diminuons .
Si la
norme ne change pas et que la
vitesse est constante , alors nous
ne changeons pas .
S'il est
inférieur à la normale et
diminue et que
le taux de chute augmente , alors
augmentez .
Si vous comprenez ce qui est vraiment caché derrière le brouillard mathématique, alors vous pouvez aborder la création de régulateurs plus consciemment et obtenir des résultats plus intéressants.
Un peu de théorie
Pour résoudre le problème d'ajustement de l'angle d'attaque, nous devons obtenir trois termes à partir de la valeur d'écart continu - moins, norme, plus. Il en va de même pour la première dérivée de l'écart et la seconde dérivée de l'écart. Il s'agit de la première étape de l'inférence floue - le phasage.
Pour obtenir les termes, nous devons définir la valeur numérique du paramètre pour chaque terme. Par exemple: "Little" = -1; "Norm" = 0; «Beaucoup» = 1. Pour le phasage, nous utiliserons des fonctions triangulaires. Les fonctions augmentent à mesure que vous approchez de la valeur définie et diminuent à mesure que vous vous éloignez. La figure 5 présente deux options pour les fonctions triangulaires:

 Figure 5. Fonctions d'appartenance triangulaire.
Figure 5. Fonctions d'appartenance triangulaire.Connaissant l'écart (x1), nous pouvons trouver les valeurs de la fonction d'appartenance pour les termes plus (ligne rouge), norme (ligne verte), moins (ligne bleue). Les valeurs vont de 0 à 1.
Veuillez noter que sur le graphique de gauche, les fonctions extrêmes ne sont pas tout à fait «triangulaires». Si nous le considérons du point de vue des mathématiques abstraites, alors les fonctions sur le graphique de droite sont plus "belles". Mais, si vous vous souvenez du "secret principal des règles d'inférence floue", le graphique de gauche est plus correct. En fait:
Considérez la règle
"Ajouter - petit" , si nous avons une valeur de -1, alors
"petit" = 1 (ligne rouge) est vrai pour les deux graphiques. Et si nous avons une valeur de -2? Logiquement, nous devons également
ajouter . Sur le graphique de gauche à -2, c'est:
«petit = 1» , mais sur le graphique de droite, nous avons
«petit» = 0, ce qui n'est évidemment pas vrai. Il en va de même pour la règle
"réduire beaucoup" .
La mise en phase par des fonctions triangulaires «honnêtes» peut conduire au fait que lorsque la valeur dépasse la plage de définition des fonctions, nous obtenons 0 pour tous les termes, ce qui, à son tour, peut conduire à l'absence d'impact sur l'objet.
Le problème inverse est la déphasification. Pour calculer l'impact, vous devez effectuer la transformation inverse - nous avons les valeurs des fonctions d'appartenance pour réduire, pas changer, augmenter la plage (
0 ... 1 ) (fonctions triangulaires) et la plage d'effets que nous pouvons avoir, et nous devons obtenir l'un des trois termes le nombre est un impact spécifique.
Vous pouvez obtenir l'impact de différentes manières, par exemple au centre de gravité de la figure. La figure 6 montre l'état du contrôleur, où les valeurs des termes diminuent de
0,3 ne changent pas de
0,6 et augmentent de
0,8 avec une plage d'impact réglementaire
-30..30 impact résultant =
4.1.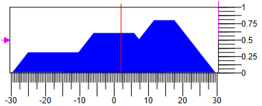 Figure 6. Défazification de l'action de contrôle
Figure 6. Défazification de l'action de contrôleUne autre option pour la défazification est dans le centre de masse des points. La figure 7 montre une option où, pour les mêmes valeurs des termes et de la plage de contrôle, nous obtenons une autre réponse
8.82 :
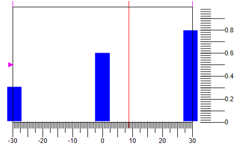 Figure 7. Défazification par le centre de masse des points.
Figure 7. Défazification par le centre de masse des points.Il faut comprendre qu'en plus de la méthode d'inférence, la forme de la fonction d'appartenance affecte également le résultat. Par exemple, vous pouvez choisir de telles fonctions triangulaires pour lesquelles la base du triangle est la même, seuls les sommets diffèrent. (voir fig.8).
 Figure 8. Fonctions d'appartenance triangulaire avec une seule base.
Figure 8. Fonctions d'appartenance triangulaire avec une seule base.Dans ce cas, pour réduire le résultat de la phasage avec les mêmes valeurs des termes 0,3, ne changez pas 0,6 et augmentez -0,8 avec la plage d'impact réglementaire -30, 30 impact résultant =
5,27 .
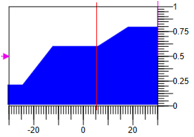 Figure 9. Calcul de la défazification par zone.
Figure 9. Calcul de la défazification par zone.Armé d'une connaissance secrète de la logique floue, nous allons créer un modèle de contrôleur. Nous laissons le modèle de fusée identique à celui du contrôleur PID (voir Fig.1), mais dans le sous-modèle du contrôleur, nous assemblons le circuit illustré à la figure 10.
 Figure 10. Le circuit du contrôleur basé sur une logique floue.
Figure 10. Le circuit du contrôleur basé sur une logique floue.A l'entrée du régulateur, un décalage entre l'angle d'attaque donné et le réel (mesuré) est appliqué. Après l'entrée, il y a un bloc "Extrapolateur", qui fournit la conversion d'un signal continu en un signal discret avec une période d'échantillonnage donnée (0,001 s est le même que celui d'un contrôleur PID discret).
Après cela, les écarts de dérivée première et seconde sont calculés. Pour ce faire, nous calculons la différence entre la valeur actuelle et la valeur avec un retard pour la période de quantification, la divisons par le temps de retard (coefficient dans le bloc de comparaison). Ainsi, nous obtenons trois entrées: erreur système, taux de variation (dérivée première) de l'erreur, accélération (dérivée seconde) de l'erreur.
La valeur des variables d'entrée est convertie par des blocs de phase en fonctions triangulaires. Pour chaque variable, nous obtenons trois variables linguistiques (neuf au total).
Le démultiplexeur bloque les vecteurs de race en variables linguistiques pour former des règles. Dans le diagramme, les noms des variables sont signés dans l'ordre de leur ordre dans les vecteurs.
L'écart dans notre cas est la différence entre l'ensemble et la mesure, si une valeur négative signifie que l'angle d'attaque est supérieur à l'ensemble, nous devons le réduire. Et en conséquence, au contraire, si l'écart est positif, alors l'angle mesuré est inférieur à celui spécifié, il faut l'augmenter.
(Plus - réduire, moins - augmenter, la norme - ne pas toucher) .
La sortie a également trois variables linguistiques «réduire», «ne pas changer», «augmenter». Le multiplexeur collecte les valeurs dans un vecteur et les envoie au bloc de sortie flou. Maintenant que nous avons toutes les variables, nous pouvons écrire les règles d'inférence floue sous la forme d'un diagramme.
- Si plus que la normale et l' écart augmente et le taux de croissance augmente => diminue.
- Si la norme ne change pas et est constante => nous ne changeons pas.
- S'il est inférieur à la normale et diminue et que le taux de chute augmente => augmenter.
Toutes les variables linguistiques des règles sont connectées via les blocs logiques «et» et connectées aux sorties. Comme on peut le voir sur la figure 10, le circuit d'inférence floue logique n'est pratiquement pas différent du circuit logique habituel, seuls les blocs de logique floue sont utilisés.
Comme pour le réglage du contrôleur PID, nous utilisons le bloc d'optimisation.
La question demeure avec les paramètres des blocs.
Synthèse d'un contrôleur basé sur la logique floue
Rien n'est donné dans la vie pour rien, et par conséquent, la simplicité des règles de régulation est compensée par le nombre de paramètres qui décrivent les fonctions d'appartenance. En fait, si vous devez sélectionner trois coefficients pour le contrôleur PID, alors dans le cas de la logique floue, une seule fonction triangulaire a besoin de 3 nombres pour les sommets. Si pour chaque variable d'entrée, nous avons besoin de 3 fonctions d'appartenance + 3 pour la sortie, il s'avère que nous devons définir 3 x 3 x 3 + 3 x 3 = 36 paramètres!
Mais tout n'est pas si triste. Pour une première approximation et une configuration initiale, tout peut être simplifié.
Après avoir fait quelques hypothèses pour le réglage initial du contrôleur:
- Nous définissons la symétrie des fonctions par rapport à zéro, puis au lieu de deux nombres pour le maximum et le minimum, vous pouvez spécifier un - Max , et, en conséquence, sera défini comme une plage [ -Max ... Max ].
- Nous définissons une distribution uniforme des fonctions, puis nous pouvons calculer la position de tous les sommets des triangles en fonction d'une plage donnée.
- Pour trois fonctions, les coordonnées des sommets sont définies comme –Max, 0, Max.
- Nous définissons que la base du triangle de toutes les fonctions d'appartenance est la même.
Ainsi, au lieu de 36 paramètres indépendants, nous ne devons spécifier que 4, l'écart maximum par rapport à 0 pour trois variables d'entrée et une sortie, à savoir:
uMax - amplitude de l'action de contrôle
(-uMax ... uMax) ;
deltaMax - écart maximum
(-deltaMax ... deltaMax) ;
divMax - dérivée maximale de l'écart
(-divMax ... divMax) ;
div2Max - dérivée seconde maximale de l'écart
(-div2Max ... div2Max)Dans les fonctions de phasage et d'inférence floue, nous utilisons ces signaux pour calculer les paramètres en tenant compte des hypothèses acceptées.
Paramètres du contrôleur proposés dans le livre de V.V. Gostev «Régulateurs flous dans les systèmes de modélisation automatique», pour le cas de la phasage par trois fonctions d'appartenance, les paramètres suivants sont proposés:
uMax = 30 - l'amplitude de l'action de contrôle;
deltaMax = 0,01 - écart maximum;
divMax = 0,07 - dérivée maximale de l'écart;
div2Max = 1 est la dérivée seconde maximale de l'écart.
Comparaison transitoire
Sur le graphique des transitoires, la coïncidence d'un effet donné et du résultat obtenu est presque complète:

Figure 11.a Transitoire. Contrôleur PID
| 
Figure 11.b Transitoire. Logique floue
|
Des différences évidentes peuvent être vues sur les graphiques de l'écart obtenu et de l'action de contrôle:

Figure 12.a. La gestion. Contrôleur PID
| 
Figure 12.b. La gestion. Logique floue |
À partir d'une comparaison des figures, on voit que le contrôleur flou fournit moins d'erreur et un meilleur transitoire.
Comparons les transitoires dans le système si nous définissons une action de contrôle pas à pas. Les résultats de la figure 13:

Figure 13.a. Effet de pas. Contrôleur PID.
| 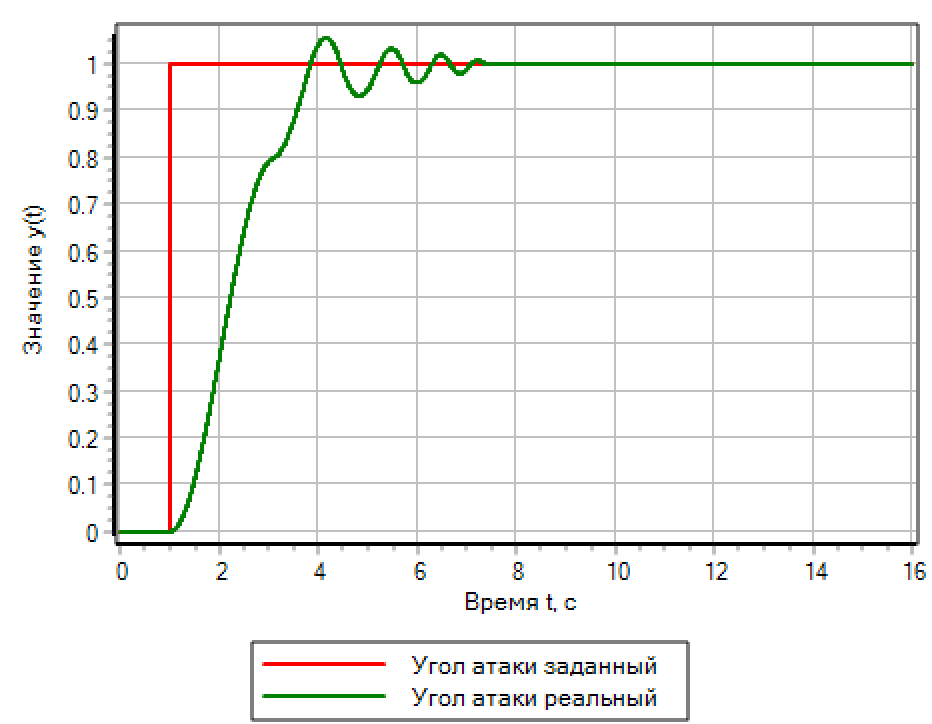
Figure 13.b. Effet de pas. Logique floue. |
Pour une action pas à pas, un contrôleur basé sur une logique floue offre la meilleure qualité transitoire. Le contrôleur PID, qui est automatiquement réglé sur un processus sans heurt, provoque des oscillations avec dépassement qui sont deux fois le pas défini.
Réglage du contrôleur basé sur la logique floue par méthode d'optimisation
Essayons de sélectionner les paramètres du contrôleur flou par la méthode d'optimisation, tout comme nous les avons sélectionnés pour le contrôleur PID. Comme critère, nous fixons l'écart type à moins de 0,001.
Il convient de noter que cette méthode n'est pas entièrement correcte, car pour les professionnels, il est clair quels angles et quelles vitesses sont le maximum et le minimum pour chaque pièce de concert, ce qui vous permet de définir plus consciemment les restrictions sur les paramètres optimisés, nous définissons les paramètres par défaut et voyons ce qui se passe.
La méthode d'optimisation avec les paramètres par défaut a calculé les valeurs suivantes des plages de paramètres d'optimisation:
uMax = 19,377 - l'amplitude de l'action de contrôle;
deltaMax = 1.095 - écart maximum;
divMax = 0,01 - dérivée maximale de l'écart;
div2Max = 2.497 est la dérivée seconde maximale de l'écart.
Dans le cas d'une simple optimisation de l'écart, les paramètres obtenus fournissent la précision spécifiée, cependant, cela provoque des oscillations à haute fréquence de l'action de commande.
La fonction de transition et les actions de contrôle sont présentées dans la figure 14.a
 Figure 14.a. Logique floue. Réglage de l'écart. Figure 14.a. Logique floue. Réglage de l'écart.
| 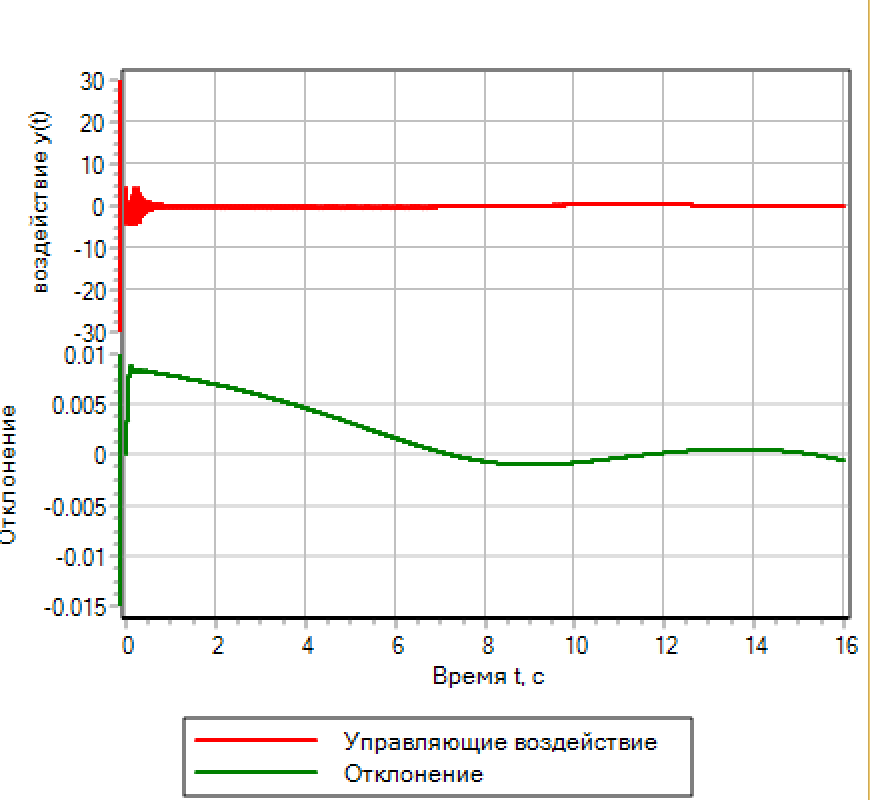 Figure 14.b. Logique floue. Réglage par écart et nombre de réponses. Figure 14.b. Logique floue. Réglage par écart et nombre de réponses. |
Afin d'améliorer le processus transitoire, on peut ajouter au critère d'optimisation le nombre de commutations du régulateur de la valeur négative à la valeur positive de l'effet de régulation (schéma de la figure 15).
 Figure 15. Schéma d'optimisation selon 2 critères.
Figure 15. Schéma d'optimisation selon 2 critères.Le calcul par la méthode d'optimisation selon deux critères donne les valeurs de paramètres suivantes:
uMax = 19,714 - l'amplitude de l'action de contrôle;
deltaMax = 1,0496 - écart maximal;
divMax = 0,01 - dérivée maximale de l'écart;
div2Max = 1,7931 est la dérivée seconde maximale de l'écart.
On peut voir que lorsque le nombre de déclenchements a été ajouté au critère d'optimisation, il a été possible de réduire la fréquence de commutation du régulateur (voir Fig. 14.b). Ainsi, nous pouvons dire que la méthode d'optimisation fonctionne même lorsque nous ne savons rien de la physique de l'objet et sélectionnons simplement les paramètres numériques sans penser à leur signification physique.
Création de votre propre contrôleur basé sur une logique floue
Ci-dessus, nous avons créé le contrôleur selon un schéma déjà préparé et assez simple, tous les termes des variables linguistiques ont été connectés par l'opérateur logique I. Puisque nous avons le même nombre de termes aux entrées et sorties, c'est la solution la plus simple et la plus évidente.
Essayons de créer un contrôleur dont la sortie n'a pas 3 termes, mais, par exemple, 5:
réduire rapidement, réduire, ne pas changer, augmenter, augmenter rapidement . Et à l'entrée la même chose.
Modifions la logique du régulateur, pour commencer, en simplifiant au maximum l'algorithme de contrôle.Nous écrivons les règles:1) Si elle est plus grande et croît t => décroît rapidement.2) Si plus => diminuer.3) Si la norme => ne change pas.4) Si moins => augmenter.5) Si moins et ont menshaetsya => augmentation rapide.Dans ce cas, nous avons 5 termes (5 fonctions triangulaires) pour la variable de sortie. Nous acceptons qu'ils soient également répartis entre -uMax et + uMax.Nous supposons que les fonctions triangulaires sont composées de telle manière que lorsque les fonctions d'appartenance du terme prennent des valeurs maximales, les fonctions voisines prennent des valeurs nulles (voir Fig. 5).En tant que paramètres de sortie, seuls l'écart et le taux de variation de l'écart seront utilisés.Pour accélérer les calculs, nous utilisons le phasage de sortie de la méthode par le centre de gravité des points (voir Fig. 7).Le circuit du contrôleur dans ce cas ressemblera à celui illustré à la figure 15.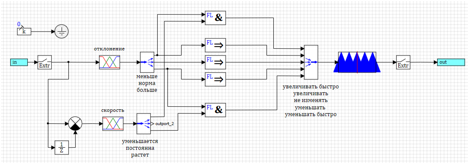 Figure 15. Un contrôleur simplifié basé sur une logique floue.Au lieu de la plage de la dérivée seconde de l'optimiseur, la valeur du terme "augmentation" sera prise. Une tentative de réglage d'un tel régulateur par la méthode d'optimisation montre que le régulateur est réglé, mais la qualité de la régulation du contrôle du système laisse beaucoup à désirer.Le meilleur résultat est illustré à la figure 16.
Figure 15. Un contrôleur simplifié basé sur une logique floue.Au lieu de la plage de la dérivée seconde de l'optimiseur, la valeur du terme "augmentation" sera prise. Une tentative de réglage d'un tel régulateur par la méthode d'optimisation montre que le régulateur est réglé, mais la qualité de la régulation du contrôle du système laisse beaucoup à désirer.Le meilleur résultat est illustré à la figure 16.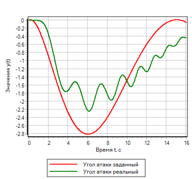 Figure 16. Transitoire pour un contrôleur simplifié.On peut voir que la régulation est en cours, mais pas du tout comme nous le souhaiterions. Le fait est que nous exerçons l'effet lorsqu'une déviation s'est déjà produite. Essayons d'activer la régulation au moment où nous avons un écart dans la norme, mais la vitesse montre qu'elle va augmenter ou diminuer.1) Si moins et diminue => augmenter rapidement.2) Si la norme et augmente => diminuer.3) Si la norme => ne change pas.4) Si la norme et diminue => augmenter.5) Si plus gros et en croissance => diminuer rapidement.
Figure 16. Transitoire pour un contrôleur simplifié.On peut voir que la régulation est en cours, mais pas du tout comme nous le souhaiterions. Le fait est que nous exerçons l'effet lorsqu'une déviation s'est déjà produite. Essayons d'activer la régulation au moment où nous avons un écart dans la norme, mais la vitesse montre qu'elle va augmenter ou diminuer.1) Si moins et diminue => augmenter rapidement.2) Si la norme et augmente => diminuer.3) Si la norme => ne change pas.4) Si la norme et diminue => augmenter.5) Si plus gros et en croissance => diminuer rapidement.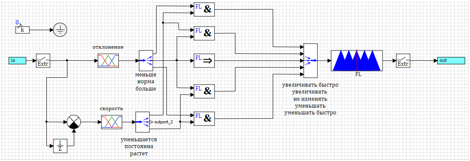 Figure 17. Contrôle par le taux de variation de l'écart.Les résultats du fonctionnement du contrôleur réglé par la méthode d'optimisation sont présentés sur les figures 18a et 18b.
Figure 17. Contrôle par le taux de variation de l'écart.Les résultats du fonctionnement du contrôleur réglé par la méthode d'optimisation sont présentés sur les figures 18a et 18b.
Figure 18.a. Le processus de transition.
| 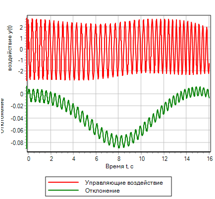
Figure 18.b. La gestion |
Le contrôle du taux de variation de l'écart a considérablement amélioré le transitoire. Cependant, si vous regardez attentivement l'ensemble des règles logiques, nous voyons que l'écart n'est pas impliqué dans la gestion. Si un effet de pas est donné, le contrôleur de contrôle ne générera pas d'action de contrôle. La figure 19 montre un exemple d'un processus transitoire avec une action de contrôle par étapes, on peut voir que le contrôleur ne donne pas d'action de contrôle, bien que l'écart soit de 1.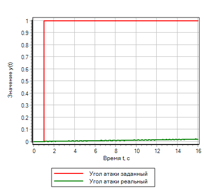
Figure 19.a. Le processus de transition. Étape
| 
Figure 19.b. La gestion. Étape |
Afin de déterminer les écarts rapides, nous ajoutons une action de contrôle des écarts. Nous augmenterons si moins et diminuerons si plus. Puisqu'il y a déjà des règles dans l'ensemble de règles sous lesquelles nous réduisons et augmentons, nous utilisons l'opérateur logique ou:1) Si moins et diminue => augmenter rapidement.2) Si ( norme et augmente ) ou plus => diminuer.3) Si la norme => ne change pas.4) Si ( norme et diminue ) ou moins => augmenter.5) Siplus grand et en croissance => diminue rapidement.Le circuit du contrôleur selon ces règles est présenté sur la figure 20.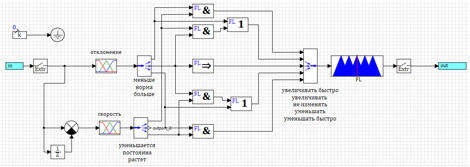 Figure 20. Un contrôleur avec contrôle par déviation et taux de variation.À la suite de la modification, la qualité du processus de transition avec une action en douceur n'a pratiquement pas changé, cependant, avec une action par étapes, le régulateur a commencé à calculer l'étape et à amener l'angle d'attaque de la fusée à celui spécifié (voir Fig.21).
Figure 20. Un contrôleur avec contrôle par déviation et taux de variation.À la suite de la modification, la qualité du processus de transition avec une action en douceur n'a pratiquement pas changé, cependant, avec une action par étapes, le régulateur a commencé à calculer l'étape et à amener l'angle d'attaque de la fusée à celui spécifié (voir Fig.21).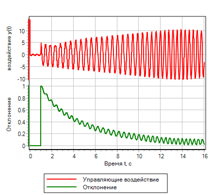
Figure 21.a. Le processus de transition. Étape
| 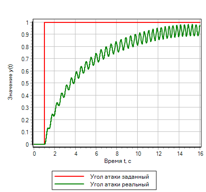
Figure 21.b. La gestion. Étape |
En conclusion, «améliorons» encore une fois notre régulateur.Essayons d'utiliser la dérivée seconde de la déviation, pour démarrer l'impact, avant que la déviation et sa vitesse aient changé. En fait, avec l'application de la force, nous avons une accélération à laquelle nous pouvons déjà répondre.Essayons d'ajouter la dérivée seconde à la loi de régulation au lieu de la dérivée première de la vitesse. Nous aurons un effet réglementaire supplémentaire dans le cas où notre dérivé second montrera qu'il y aura un écart. Les règles générales seront presque identiques, seulement entre parenthèses, nous avons trois termes, l'écart et la vitesse sont normaux et la dérivée seconde s'écarte:1) Si moins et diminue => augmenter rapidement.2) Si (normal et constant et accélère ) ou plus => diminuer .3) Si la norme => ne change pas.4) Si ( normal et constant et ralentit ) ou moins => augmenter.5) Si plus gros et en croissance => diminuer rapidement .Le circuit de ce régulateur est illustré à la figure 22. Pour économiser de l'espace sur le circuit, les expressions logiques «et» écrites entre parenthèses sont calculées dans le sous-modèle marqué « & ».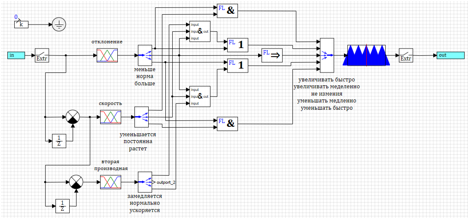 Figure 22. Contrôleur à logique floue avec contrôle de la dérivée seconde.Après avoir sélectionné les paramètres par la méthode d'optimisation de l'écart et du nombre d'inclusions, les paramètres suivants ont été obtenus:uMax = 27,4983 - l'amplitude de l'action de contrôle;deltaMax = 0,0433 - écart maximal;divMax = 0,0966 - dérivée maximale de l'écart;div2Max = 1,0828 - la dérivée seconde maximale de l'écart.Le processus transitoire est illustré à la figure 23. On peut voir que le régulateur résultant a les meilleures performances de tous ceux considérés ci-dessus, mais pour un effet donné. Les écarts et les actions de contrôle sont le minimum de tous considérés dans ce texte.
Figure 22. Contrôleur à logique floue avec contrôle de la dérivée seconde.Après avoir sélectionné les paramètres par la méthode d'optimisation de l'écart et du nombre d'inclusions, les paramètres suivants ont été obtenus:uMax = 27,4983 - l'amplitude de l'action de contrôle;deltaMax = 0,0433 - écart maximal;divMax = 0,0966 - dérivée maximale de l'écart;div2Max = 1,0828 - la dérivée seconde maximale de l'écart.Le processus transitoire est illustré à la figure 23. On peut voir que le régulateur résultant a les meilleures performances de tous ceux considérés ci-dessus, mais pour un effet donné. Les écarts et les actions de contrôle sont le minimum de tous considérés dans ce texte.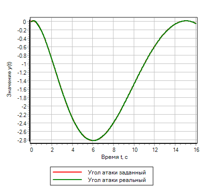
Figure 23.a. Le processus de transition.
| 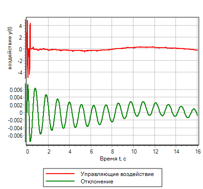
Figure 23.b. La gestion. |
Conclusions
Un contrôleur basé sur la logique floue peut fournir un transitoire de meilleure qualité pour le contrôle de fusée qu'un contrôleur PID.Le réglage du contrôleur basé sur une logique floue peut être effectué à l'aide d'outils d'optimisation.Un contrôleur basé sur une logique floue offre une plus grande flexibilité dans le réglage et une meilleure qualité transitoire. Mais cela nécessite de définir plus de paramètres.Téléchargez l'archive des modèles utilisés dans la préparation de ce texte, pour étude indépendante ici ...