Génération de clés hiérarchiques

Dans cet article, nous parlerons des portefeuilles déterministes, de la génération de clés hiérarchiques et de la façon dont cela fonctionne mathématiquement et dans quels cas il est pratique de les mettre en pratique. Ce matériel sera utile aux spécialistes dont les activités sont liées aux passerelles de paiement, aux portefeuilles Bitcoin et à d'autres magasins de pièces. En outre, le matériel sera intéressant pour ceux qui sont intéressés par les schémas de déploiement de clés de cryptographie elliptique et de signature électronique.

Portefeuille déterministe

Tout d'abord, définissons ce qu'est un portefeuille déterministe. Lorsque nous parlons de génération de clés, nous utilisons souvent le mot «portefeuille», car dans le contexte des crypto-monnaies, la possession d'une clé privée est la preuve de la propriété des pièces, et dans ce cas, le portefeuille et la clé ont une signification similaire.

Le portefeuille déterministe est un portefeuille dans lequel toutes les clés privées utilisées ont été générées à partir d'un secret partagé par toutes les clés. La particularité est qu'il est possible à partir d'un secret de générer un nombre quelconque de paires de clés pour la signature électronique. Vous pouvez utiliser de nouvelles adresses pour chaque paiement et modification entrants.

De manière pratique, les clés d'un tel portefeuille peuvent être facilement transférées vers un autre appareil, faites une copie de sauvegarde puis restaurées, car en fait, vous n'avez besoin de réserver qu'un seul secret principal. De plus, toutes les clés privées générées à partir du secret principal ne sont pas connectées les unes aux autres. Il est impossible de tracer la connexion entre les adresses générées (pour déterminer qu'elles appartiennent toutes à un utilisateur) et, ayant la clé privée générée, vous ne pouvez pas restaurer le secret partagé.

Encodage secret de base

Parlons maintenant de l'encodage du secret principal. Il existe une approche standardisée définie dans le BIP39. Il s'agit de l'encodage Check Encoding du secret principal en une phrase mnémonique - un ensemble de mots faciles à écrire sur papier et, si nécessaire, à retenir. Lors de la saisie, il est possible de vérifier la somme de contrôle, c'est-à-dire d'identifier une erreur, le cas échéant, avec une probabilité assez élevée.



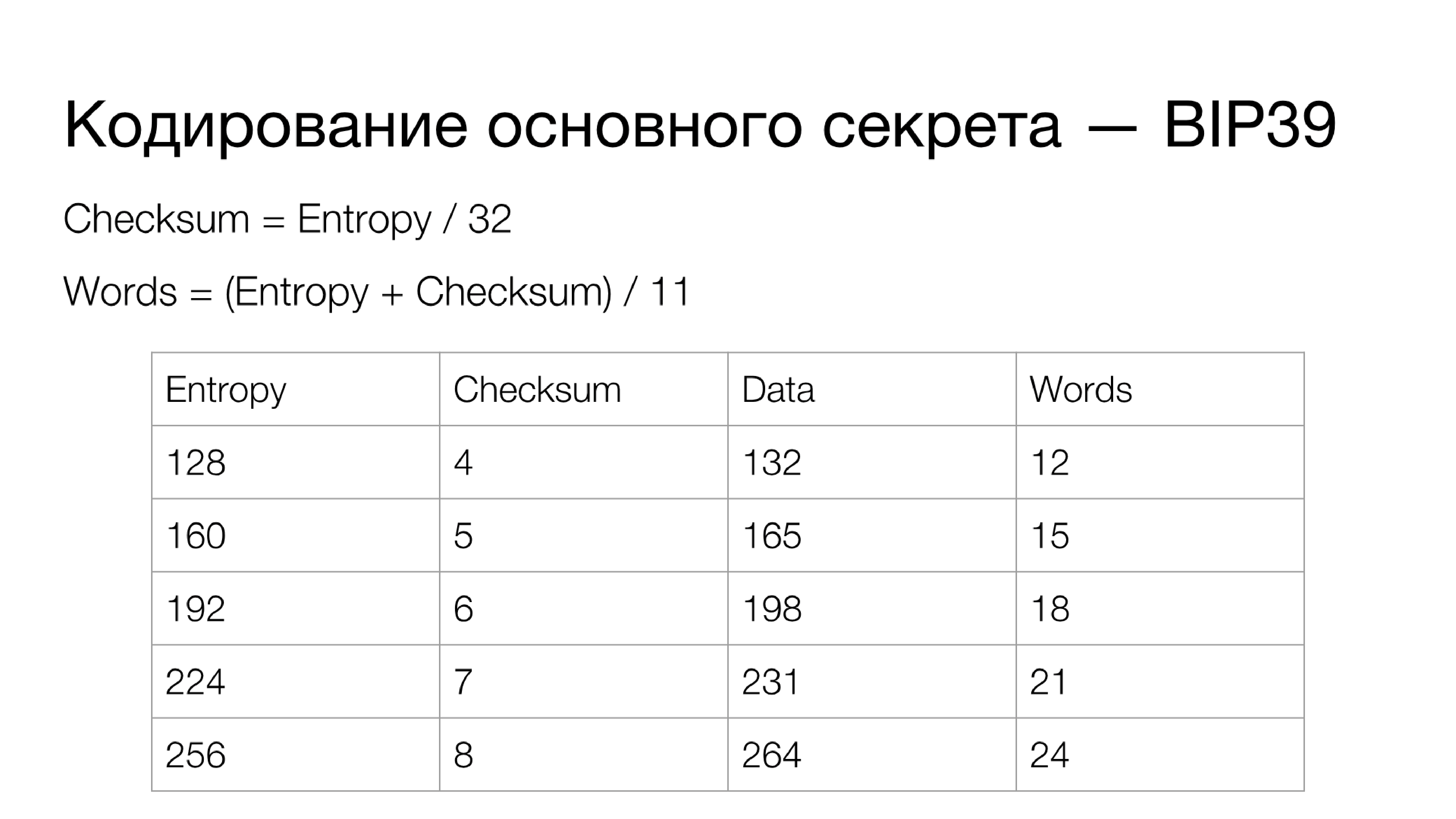
Comment ça marche? En fait, vous avez le secret principal (Entropie) - les données à partir desquelles toutes les clés personnelles du portefeuille sont développées. Ce secret peut avoir différentes longueurs. En ce qui concerne la somme de contrôle: pour chaque 32 bits d'entropie, il y a 1 bit de la somme de contrôle, c'est-à-dire que la somme de contrôle est calculée par la formule comme la longueur de l'entropie en bits divisée par 32.

L'entropie concatène avec une somme de contrôle, qui est calculée comme un double hachage SHA-256 (SHA-2 sur une longueur de 256 bits), après quoi le nombre requis de bits est coupé. Les données concaténées sont transférées vers un autre système numérique: du binaire au système numérique sur la base de 2048 (comme vous pouvez le voir, 2048 est $$$2 ^ {11}$) Et si vous ajoutez la longueur des bits d'entropie et la somme de contrôle, vous obtenez un multiple de 11. Ainsi, nous obtenons le nombre de mots dans la phrase mnémonique de sortie.

En fait, les données sont «découpées» en parties de 11 bits. Il existe un dictionnaire de 2048 mots ( $$$2 ^ {11}$) auxquels s'appliquent certaines exigences. La langue par défaut du dictionnaire est l'anglais, mais n'importe qui peut être utilisé. Les mots ne doivent pas dépasser une certaine longueur (généralement une limite de 7 caractères maximum). Tous doivent être encodés en UTF-8 avec une certaine normalisation de tous les caractères. Obligatoire est l'unicité de chaque mot dans les quatre premiers caractères.

Les quatre premiers caractères identifient de manière unique le mot dans le dictionnaire, et les caractères restants sont utilisés pour compléter ce mot sous une forme pratique pour la lecture, la mémorisation, etc. Ainsi, chaque donnée composée de 11 bits reçoit une correspondance non ambiguë sous la forme d'un mot de dictionnaire. Si l'entropie de votre secret est de 256 bits, alors les données pour l'encodage seront de 264 bits, et votre phrase mnémonique contiendra 24 mots. Il s'agit de l'approche principale pour chiffrer les secrets de portefeuille dans BIP39, qui est le plus souvent utilisée dans la pratique.

Afin de faire une copie de sauvegarde à l'avenir et de l'utiliser, vous êtes invité à écrire cette phrase sur un support externe. Le papier que vous stockerez dans un endroit sûr est le meilleur. Ainsi, vous pouvez restaurer un accès complet à toutes vos clés.

Types de portefeuilles déterministes

Les portefeuilles déterministes sont de deux types. Considérez leurs principales différences.

Le premier est le plus simple. Le secret principal ici est concaténé avec l'index de la clé enfant que nous voulons obtenir, après quoi les données concaténées sont hachées. Le plus souvent, cela se produit en utilisant la fonction de hachage SHA-256.

Le deuxième type comprend les portefeuilles déterministes hiérarchiques, les portefeuilles HD, dont les principes sont définis dans BIP32, et constituent une approche très courante de la génération de clés hiérarchiques.

Génération déterministe

Considérez les différences entre ces types de portefeuilles dans le diagramme.



Un portefeuille déterministe ordinaire a des graines, à partir desquelles un grand nombre de clés privées sont directement générées. Leur nombre ne peut être limité que par la dimension de l'index, qui concatène au secret avant hachage. Habituellement, il est de 4 octets, c'est-à-dire que l'espace des options possibles permet environ 4 milliards de clés de portefeuille déterministes uniques. En pratique, cela devrait être suffisant pour toute situation.

Génération déterministe hiérarchique

Passons maintenant à un portefeuille déterministe hiérarchique, dont le schéma de déploiement clé est présenté jusqu'à présent sous une forme simplifiée. Il existe une graine à partir de laquelle une paire de clés principales est directement obtenue. Si dans un portefeuille déterministe ordinaire, nous obtenons une clé privée, alors nous obtenons ici une paire de clés. De plus, il existe des niveaux de hiérarchie, à chacun desquels nous calculons l'index pour générer la clé enfant. Nous pouvons également créer des branches de clé publique et des branches de clé privée.

Niveaux de hiérarchie

En ce qui concerne les portefeuilles HD, il convient de noter que selon les règles BIP32 à chaque niveau de la hiérarchie, un nœud de génération a trois objets: une clé privée, une clé publique et un code de chaîne utilisé pour générer le niveau de hiérarchie suivant.

Schéma de génération hiérarchique

Examinons plus en détail le schéma de génération de clés pour BIP32.



Tout commence par la graine, elle est également appelée graine principale, à partir de laquelle le niveau zéro de la hiérarchie est calculé - une paire de clés principales et un code de chaîne.

Un grand nombre de paires de clés avec des indices spécifiques peuvent être générées à partir d'une paire de clés principales. Un nouveau niveau de hiérarchie est en cours de formation, qui est utilisé pour générer des comptes. Supposons qu'un utilisateur ait une graine et souhaite créer plusieurs adresses qui seront différentes les unes des autres. Les pièces de ces adresses ne seront pas mélangées, ne seront pas publiées ensemble et dans les transactions terminées entre elles, il ne sera pas possible de trouver une connexion. Ces clés seront utilisées complètement séparément les unes des autres. Dans l'un des comptes, le groupe clé sera utilisé pour le budget de travail, dans l'autre pour le budget personnel et un autre compte pour la comptabilité noire. Les pièces ne se mélangeront pas entre elles.

Le niveau de hiérarchie suivant définit différentes chaînes de génération de clés. Le plus souvent, des chaînes avec les indices 0 et 1. Une chaîne avec l'index 0 générera les clés finales pour former une adresse pour les paiements entrants, et une chaîne avec l'index 1 générera des portefeuilles pour les pièces envoyées par l'utilisateur à lui-même, c'est-à-dire le changement. Cela est nécessaire pour que le portefeuille au niveau du programme distingue les paiements envoyés de l'extérieur du changement, calcule les changements dans le solde de chaque transaction et compile une liste visuelle avec l'historique de tous les paiements. Cela simplifie le développement du portefeuille et son utilisation pour les paiements quotidiens.

Code d'authentification de message basé sur le hachage

Passons maintenant à la composante mathématique des processus de génération de clés hiérarchiques. Pour commencer, considérez le code d'authentification de message basé sur le hachage. Il s'agit d'une classe différente pour le calcul des fonctions de hachage. Il diffère en ce qu'il prend deux valeurs à l'entrée, et non une. La première valeur est la clé privée et la seconde est le message lui-même.

$$

$$HMAC (K, m) = H ((K ^ {opad}) || H (K ^ {ipad}) || m))$$

K est la clé
m - message
opad, ipad - certaines valeurs constantes nécessaires pour générer des clés différentes les unes des autres à différents stades de hachage.
En tant que fonction de hachage, SHA-512 est utilisé.

La particularité est que pour utiliser HMAC, vous devez posséder une clé secrète afin d'obtenir la valeur de hachage correcte du message.

Ainsi, pour calculer la valeur de hachage HMAC, la valeur de la clé XOR est avec la valeur constante ipad, après quoi le résultat est haché. Un message est concaténé à cette valeur, après quoi la clé XOR est calculée avec une valeur constante, concaténée avec une valeur de hachage, puis hachée à nouveau. En conséquence, nous obtenons 512 bits de la valeur de hachage.

Fonctions de dérivation

Examinons quelques fonctions utilisées dans le calcul des clés hiérarchiques.



Tout d'abord, nous souhaitons convertir la graine maître en une paire de clés maîtresse. Après cela, vous devez obtenir la clé privée enfant et la clé publique enfant de la clé parent personnelle. Dans le deuxième cas, la même fonction exacte est utilisée que dans le premier, mais la multiplication du nombre par le point de base est ajoutée, elle ne sera donc pas considérée séparément. L'étape suivante consiste à obtenir le public enfant à partir de la clé parent publique. Il convient de noter qu'il n'est pas possible d'obtenir un enfant personnel à partir de la clé publique parent. Cette limitation est due à certaines propriétés inhérentes aux portefeuilles HD, que nous examinerons plus loin.

Passons donc en revue chacune des fonctions de génération séparément.



Pour obtenir la clé principale du sid maître, la fonction HMAC est utilisée, où la chaîne constante "Bitcoin seed" est transmise comme clé et les données secrètes principales elles-mêmes comme message. Ainsi, une valeur de hachage de 512 bits est obtenue, que nous considérons comme deux parties: gauche et droite. Le côté gauche est la clé privée principale et le côté droit sera le code de chaîne. De plus, ces valeurs seront utilisées pour générer des niveaux ultérieurs de clés enfants.

Pour obtenir le maître public, multipliez simplement la valeur du point de base par la valeur de la clé privée principale. Comme vous pouvez le voir, cela se produit par analogie avec des touches ordinaires dans un groupe de points sur une courbe elliptique.

Voyons maintenant comment la clé privée enfant provient du parent privé.



Nous utiliserons à nouveau la fonction HMAC. En tant que clé, nous transmettons le code de chaîne du niveau de hiérarchie actuel, et en tant que message, la concaténation, où la première partie sera la clé parent personnelle multipliée par le point de base. En fait, il s'agit d'une conversion en un point et d'une sérialisation de ce point. La concaténation se produit avec l'index de la clé enfant que nous voulons recevoir, sérialisé à 32 bits, soit 4 octets.

Sur la base du résultat de la fonction HMAC, nous obtenons la valeur I, et encore une fois nous la considérons séparément: les parties gauche et droite des valeurs de sortie sont de 256 bits. Ensuite, la clé privée enfant $$$k_i$nous calculons en ajoutant à la valeur de sortie gauche $$$I_l$valeurs de la clé privée parent. L'addition se fait modulo n, où n est l'ordre du point de base de la courbe elliptique, afin de ne pas dépasser la valeur maximale de la clé privée. Ainsi, nous avons reçu une clé privée enfant.

En conséquence, le code de chaîne enfant sera égal à la valeur de sortie droite de la fonction HMAC, c'est-à-dire $$$I_R$. Si nous voulons trouver la clé publique enfant à partir de la clé parent personnelle, nous multiplions la valeur $$$k_i$par la valeur du point de base sur la courbe elliptique. Nous obtenons donc la clé publique $$$K_i$.

Comment calculer la clé publique enfant à partir de la clé parent publique?



Ici, le calcul sera un peu différent. Nous transmettons la hiérarchie de chaîne du niveau de hiérarchie actuel sous forme de clé dans la fonction HMAC, après quoi nous sérialisons la clé publique parent et la concaténons avec l'index souhaité sérialisé à 32 bits. Les données d'entrée sont obtenues exactement de la même manière que dans le cas précédent. Pour calculer la clé publique, nous prenons le côté gauche de la valeur de sortie de la fonction HMAC, et la considérons comme 256 bits pris modulo l'ordre du point de base, l'amener à un point sur la courbe elliptique, c'est-à-dire, multiplier par le point de base, puis ajouter le résultat avec la clé publique parent . Le résultat de l'ajout sera également un point, et ce sera une clé enfant publique. Le code de chaîne pour cette clé sera le côté droit de la valeur de sortie de la fonction HMAC.

Associer les clés les unes aux autres

Cela peut soulever une question logique quant à la correspondance entre les clés privées et publiques obtenues de différentes manières. Est-il vraiment possible d'obtenir exactement la même valeur à partir d'une clé publique générée par une voie publique en prenant une clé privée obtenue d'une autre manière et en la multipliant par un point de base? C'est facile à vérifier.



Si nous nous souvenons de la façon dont nous avons calculé la clé enfant personnelle et la multiplions par le point de base, c'est-à-dire conduisons à la fonction point, puis rappelons le calcul de la clé publique enfant et comparons ces calculs, nous verrons que si nous considérons la clé publique parent comme un produit du parent personnel clé du point de base, alors nous verrons que les mêmes calculs ont été effectués, juste dans un ordre différent.

Dans un cas, nous avons ajouté les clés privées et multiplié par le point de base, et dans le second cas, nous avons d'abord multiplié les valeurs par le point de base, puis nous les avons ajoutées et nous avons obtenu le résultat. Sur la base du fait que l'opération d'ajout de points sur une courbe elliptique est additive, nous pouvons dire que ces deux valeurs sont égales - nous obtiendrons la même clé publique calculée de deux manières.

Exemple de clé publique

Par souci d'intérêt, nous pouvons regarder un exemple de clé publique qui a été obtenue pour les valeurs de test et les calculs BIP32. Si notre entropie se composait de 128 bits, alors dans le système numérique hexadécimal, cela ressemblera à l'image ci-dessous.



La même valeur encodée dans la phrase mnémonique BIP39 ressemblera aux 12 mots affichés. Si vous utilisez cette phrase mnémonique comme graine principale pour la génération de clés hiérarchiques, vous obtiendrez une telle clé privée principale avec le code de chaîne 256 bits correspondant.

Touches étendues

Il existe également des concepts tels que clé publique étendue et clé privée étendue. Comment est-il utilisé? Pour mieux comprendre, nous décrivons la situation visuelle.

Disons que nous avons un utilisateur spécifique et un service. Un service transfère des paiements, par exemple en bitcoins, à un utilisateur avec une certaine fréquence. L'utilisateur et le service sont intéressés à utiliser une nouvelle adresse pour chaque paiement, afin de rendre difficile pour un observateur externe d'établir un fait et de confondre l'historique des interactions entre eux.

Dans le cas le plus simple, cela ressemblerait à ceci: l'utilisateur pour chaque paiement entrant génère une nouvelle paire de clés, calcule l'adresse qu'il transmet au service, après quoi le service peut générer une transaction et effectuer le paiement. Cependant, cela n'est pas pratique pour l'une ou l'autre des parties si l'intensité de ces paiements est élevée.

Clé publique étendue

Dans une situation similaire, la clé publique étendue (xPubKey) permet de se débarrasser des inconvénients. L'utilisateur peut activer un service tiers pour générer des adresses au lieu d'elles-mêmes qui seront connues du service, mais seul l'utilisateur aura des clés privées. Le service peut générer n'importe quel nombre d'adresses à l'insu de l'utilisateur et leur envoyer des fonds, et l'utilisateur peut, à sa convenance, déployer des clés privées et accéder à l'une de ces adresses.

Comment ça marche? L'utilisateur doit générer un nouveau compte au deuxième niveau de la hiérarchie de clés, calculer pour lui la clé publique et le code de chaîne pour le niveau actuel. Après cela, vous devez transférer à la fois la clé publique et le code de chaîne au service. Pour plus de commodité, l'encodage Base58Check a été introduit, dont nous avons parlé (il existe une version spéciale ici). Ensuite, la clé publique, le code de chaîne et la somme de contrôle sont concaténés. Tout cela est codé dans le système numérique de base 58 et nous obtenons une clé étendue publique déjà codée selon une certaine norme. Il commence par les caractères «xpub», qui sont facilement reconnaissables. Il ressemblera à l'image.



Un service peut accepter une telle clé et déployer des clés publiques pour l'utilisateur via BIP32, en recevoir des adresses et les payer. Cependant, seul l'utilisateur peut calculer les clés privées correspondantes.

Dérivation renforcée

Dans la génération hiérarchique des clés, il existe une dérivation renforcée. Il s'agit d'une approche qui ne permet pas le calcul des clés publiques enfants à partir de la clé publique parent correspondante. Cela diffère de la génération normale en ce que nous utilisons la concaténation du point sérialisé comme clé publique parent comme message à la fonction HMAC, et dans la dérivation renforcée, nous utilisons la sérialisation de la clé privée parent.

De plus, le calcul de l'indice est différent. L'index en génération normale est directement sérialisé en 32 bits, et en dérivation renforcée il est légèrement converti: une valeur constante lui est ajoutée $$$2 ^ {31}$qui met le bit le plus significatif à 1 (il devient facile de distinguer les types de dérivation). En conséquence, l'espace des variantes de clés possibles est le même pour la génération normale et la dérivation renforcée, et est égal à $$$2 ^ {31}$.



Ainsi, ayant une clé publique parent et une dérivation renforcée, il n'est pas possible de calculer des clés publiques enfant. Si l'attaquant reçoit la clé publique parent, il ne pourra pas calculer les clés enfants. Par conséquent, il ne pourra pas calculer les adresses et leur relation avec la clé parent reçue. Dans le cas d'une dérivation normale, c'est-à-dire, comme d'habitude, une telle fonction peut être utilisée et tracer la relation des adresses entre elles.

Chemins de génération

Parlons de la façon dont les clés peuvent être générées.



À chaque niveau de la hiérarchie, il existe un index spécifique qui définit les aspects de la génération de clés. Le chemin de la clé principale à la clé finale peut être écrit par des barres obliques sous forme d'index. Si nous parlons d'une clé privée, alors l'enregistrement commence par un petit «m», et si nous parlons de générer une clé publique, alors avec un grand «M». Si l'index est indiqué par une apostrophe, alors il faut comprendre que nous parlons de dérivation renforcée, sans apostrophe - dérivation normale.

Considérez l'un des chemins de génération de clés populaires utilisés dans BIP32, où les clés hiérarchiques ont été définies.



Il utilise un chemin où la clé principale est le niveau zéro de la hiérarchie. Voici les index des comptes qui désignent le même utilisateur, suivis des chaînes où il peut y avoir des chaînes d'adresses publiées à l'extérieur pour accepter les paiements entrants, et avec l'index 1, ces chaînes seront créées auxquelles l'utilisateur s'envoie des paiements (le plus souvent tout cela est de la reddition). L'index final sera utilisé pour générer les clés à partir desquelles les adresses seront calculées.

Afin de calculer la toute première clé avec indice 0 selon la norme BIP32, nous aurons m, 0 avec la génération de chaîne durcie - 0, indice - 0 (m / 0 '/ 0/0). Nous obtenons donc le chemin de la première clé générée hiérarchiquement.

Il y a une proposition pour améliorer Bitcoin, il s'appelle BIP43, ce qui implique d'écrire au premier niveau de la hiérarchie le numéro d'amélioration, qui offre un nouveau chemin d'apparition (m / bip_number '/ *).



Ainsi, le BIP44 est apparu, qui utilisait la caractéristique de la phrase précédente, c'est-à-dire que l'index 44 est écrit pour le premier niveau de hiérarchie, et a proposé les améliorations suivantes: dans l'index du deuxième niveau de hiérarchie, enregistrez une certaine valeur qui correspondra au type de pièce que nous utilisons pour ce portefeuille. Désormais, les clés de différentes devises peuvent être déployées et utilisées dans un seul portefeuille.



Pour Bitcoin, le chemin ressemblera à "m / 44 '/ 0' / 0 '/ 0/0", pour Bitcoin testnet - "m / 44' / 1 '/ 0' / 0/0", pour Litecoin - "m / 44 '/ 2' / 0 '/ 0/0 ”, pour Dash -“ m / 44' / 5 '/ 0' / 0/0 ”. Fait intéressant, Ethereum utilise exactement la même courbe elliptique pour calculer les clés et signer numériquement et pour son portefeuille, le chemin ressemblera à «m / 44 '/ 60' / 0 '/ 0/0».

Il y a une autre amélioration - BIP45. L'amélioration vise à déterminer les règles de génération de clés en cas d'utilisation dans des portefeuilles multisignatures et de formation d'adresses à l'aide de BIP16, c'est-à-dire P2SH. Il comprend la phrase BIP43 et indique l'index 45 au premier niveau de la hiérarchie; au deuxième niveau de la hiérarchie, il nécessite l'indication d'un signataire (cosignataire).



Par exemple, il existe une règle de multi-signature 3 sur 5. Par conséquent, il y a 5 signataires, mais pour dépenser des pièces, vous avez besoin d'au moins 3 signatures. Ainsi, chacun des signataires aura un portefeuille HD avec sa propre graine maître, et indiquera son numéro de série sur son chemin. Il peut être calculé comme un index lors du tri des clés générées au premier niveau de la hiérarchie de chaque utilisateur. Supposons qu'au premier niveau, chaque utilisateur génère des clés, qu'il échange les uns avec les autres, trie et découvre qui a quel index pour le deuxième niveau de la hiérarchie. Ceci est nécessaire afin d'éliminer davantage la nécessité d'interagir de cette manière et de générer immédiatement correctement des adresses et de connaître votre numéro de série.

Autrement dit, vous pouvez échanger une fois la clé publique étendue afin de pouvoir indépendamment, indépendamment des autres membres du groupe, former des adresses multisignatures et accepter des paiements sur celles-ci.

Des questions

Passons aux questions fréquemment posées.

- Comment les graines de maître diffèrent-elles dans différentes pièces?

Seed est un nombre généré aléatoirement, une séquence de bits, ou c'est une phrase mnémonique générée, par exemple, selon BIP39, qui est utilisée pour générer des clés. Il peut être utilisé à la fois pour une pièce et pour toute autre - il n'est pas nécessaire d'utiliser des phrases mnémoniques différentes pour différentes devises. De plus, il y a le BIP44, qui définit les règles de génération de clés pour différentes devises à partir de la même phrase mnémonique. Ces clés privées ne se recouperont pas, mais seront utilisées pour différentes adresses de différentes devises.

- Dictionnaire du BIP39, où 2048 mots pour une phrase mnémonique sont standardisés? Puis-je l'utiliser dans tous les portefeuilles et applications?

Le fait est que cette norme est décrite pour le BIP39. C'est pour BIP39 qu'il existe des dictionnaires: anglais, deux japonais, chinois, italien, russe, ukrainien, etc. C'est-à-dire que si une application prétend qu'elle utilise BIP39 et permet d'importer et d'exporter une phrase mnémonique, cela signifie qu'elle utilise également un ensemble de mots pareil. Cependant, il existe des portefeuilles qui n'utilisent pas le BIP39, mais leur propre modification. Vous devez regarder la description du portefeuille et utiliser soit standardisé, soit votre propre développement, soit le développement du service offert par le portefeuille.

- Sur les échanges et les stockages centralisés comme Coinbase, les clés de portefeuille pour tous les utilisateurs sont-elles générées à partir de la même phrase commune pour tous ou non?

C'est difficile à dire car ils n'ouvrent pas leur structure interne, mais les nouveaux services qui apparaissent peuvent soit générer des clés séparément, soit utiliser la norme BIP32, soit utiliser sa version modifiée. Les services qui existaient avant les normes de génération de clés hiérarchiques sont apparus, très probablement, continuent de générer uniquement des clés privées distinctes. C'est peut-être ainsi qu'ils sont plus faciles à gérer s'il y a un grand roulement de toutes les clés.

"La clé est-elle un point sur la courbe elliptique, c'est-à-dire deux très grands nombres X et Y?"

La clé publique - oui, c'est un point sur la courbe elliptique, et la clé privée est un nombre naturel qui montre combien de fois vous devez ajouter le point de base avec vous-même. La clé publique elle-même se compose de deux valeurs - ce sont les coordonnées X et Y, chacune ayant une taille de 256 bits.

- Qu'est-ce que le «cast to point» et la sérialisation du point et de l'index?

La réduction à un point signifie qu'il existe un nombre naturel, que nous considérons comme une clé privée. Nous ajoutons le point de base avec nous-mêmes tant de fois, c'est-à-dire que dans le groupe de points sur la courbe elliptique, seule l'opération d'addition est définie, puis nous pouvons multiplier le point par un nombre naturel. La sérialisation d'un point signifie enregistrer d'une certaine manière deux coordonnées. Il peut s'agir d'un enregistrement compressé, mais pas nécessaire. Comprimé en ce sens que l'une des coordonnées, à savoir Y est convertie en signe, les données sont alors substituées dans l'équation et regardent où se trouve le point: au-dessus ou au-dessous. Dans le cas de la sérialisation d'index, vous devez comprendre qu'un nombre régulier, qui, selon la taille, peut être écrit en octets ou en bits. Plus le nombre est élevé, plus il faudra de données. Dans le cas des calculs que nous avons examinés,un certain nombre d'une certaine longueur est requis. Vous devez le sérialiser à une longueur spécifique - 4 octets. Par conséquent, cela fait référence à la conversion de l'index en un nombre à 4 octets. Si les valeurs seniors y restent vides, elles seront alors nulles.

- Qui a proposé ces calculs pour les fonctions de dérivation des portefeuilles HD? Pourquoi de telles formules où il y a des justifications et où vous pouvez en savoir plus à ce sujet?

Vous pouvez en savoir plus sur BIP32, si vous êtes intéressé par une phrase mnémonique, puis sur BIP39, etc. Vous pouvez ouvrir GitHub et trouver un utilisateur sous le surnom de Bitcoin. Il a un référentiel Bitcoin où le code source Bitcoin est stocké, et il a un référentiel BIPs (source principale), où toutes les suggestions pour améliorer Bitcoin sont enregistrées.

Ils ont eu l'idée de faire des calculs de cette façon, car ils sont liés à un groupe de points d'une courbe elliptique. Lorsque vous vouliez obtenir une telle fonctionnalité qui vous permet de calculer séparément les branches des clés publiques et privées, tout en conservant leur correspondance, c'était l'option d'implémentation la plus simple. En fait, les développeurs ont utilisé l'option la plus simple, ce qui vous permet d'obtenir des propriétés intéressantes en utilisant la cryptographie qui a été testée par le temps. Les auteurs des améliorations proposées sont nombreux. La communauté Bitcoin, dont les participants offrent une sorte de développement d'améliorations et de transformations mathématiques, est assez importante.

- La dérivation renforcée n'est toujours qu'au deuxième niveau de la hiérarchie?

Tout dépend de la situation. Dans le cas de la génération de clés pour la multi-signature, il est logique de faire une dérivation renforcée uniquement au premier niveau de la hiérarchie. Dans le BIP44, une dérivation renforcée est appliquée aux trois premiers niveaux: au premier niveau est le numéro du BIP lui-même, au deuxième est le numéro de compte où il est pertinent, au troisième est le numéro de devise, où il a également un sens. Supposez que vous ne l'aimerez probablement pas si vous publiez la clé publique, et grâce à elle, les gens peuvent suivre toutes vos adresses en Bitcoin. Si vous utilisez un compte pour recevoir des paiements de certains services, vous pouvez divulguer cette clé et vous n'avez pas besoin d'une dérivation renforcée ici.

- Où est-il possible d'appliquer la génération de clé hiérarchique?

Vous pouvez l'appliquer lorsque vous travaillez avec l'échange afin que l'échange vous paie toujours à différentes adresses. Bien que dans ce cas, il vaut mieux organiser tout cela manuellement. C'est le plus pertinent pour les portefeuilles numériques de tous les jours, car ici, il s'agit d'un processus très simple pour créer une sauvegarde de clés privées et restaurer un portefeuille. La génération de clés pour différentes devises est également prise en charge, et la norme elle-même est déjà utilisée dans différentes implémentations de portefeuilles numériques. Les clés entre ces portefeuilles sont pratiques à transférer en utilisant la même phrase mnémonique.

Ce sujet est traité dans l'une des conférences du cours en ligne sur la blockchain « Génération de clés hiérarchiques ».