Présentation
Pour déterminer les caractéristiques balistiques-temporelles du mouvement du centre de masse du parachutiste, il faut choisir un modèle mathématique simplifié qui est tout à fait accessible pour la recherche analytique et en même temps préserve les traits les plus caractéristiques de l'objet d'origine.
Pour construire des modèles mathématiques simplifiés du mouvement du parachutiste, une analyse, une détermination, une systématisation des paramètres constants et temporels est effectuée.
Il n'existe pas actuellement de méthodes régulières et suffisamment justifiées pour construire des modèles mathématiques non linéaires.Cependant, pour résoudre des problèmes particuliers, avec la composition correcte des systèmes initiaux d'équations différentielles non linéaires, les méthodes numériques pour les résoudre peuvent donner des résultats tout à fait adéquats.
Le but de cette publication est de compiler et de résoudre numériquement des systèmes d'équations différentielles qui décrivent toutes les étapes du mouvement d'un parachutiste atterrissant d'un avion, en tenant compte de l'effet des changements d'altitude et de température de la masse volumique de l'air.
Caractéristiques balistiques-temporelles du mouvement d'un parachutiste
Les paramètres variables constants et limités comprennent:
H - la hauteur de la libération du parachutiste;
V0 - vitesse de l'avion;
k - poids, taille du parachutiste;
g est l'accélération de la gravité;
ρ est la densité de l'air;
T est la température de l'air.
Les paramètres temporaires (variables) comprennent:
tn - heure d'atterrissage,
w est la vitesse du vent;
V est la vitesse du parachutiste;
u est la vitesse des flux ascendants (descendants);
d - dérive (distance de la projection sur le sol du point d'éjection au point de toucher);
C est le coefficient de traînée de l'objet d'atterrissage;
F - section médiane de l'atterrisseur.
Étapes de saut
La première étape est une chute libre après séparation de l'avion:
 La deuxième étape
La deuxième étape est une diminution d'un parachute stabilisateur:

La propriété principale du parachute stabilisateur est la stabilisation du parachutiste dans la position la plus pratique pour le parachute principal.
La troisième étape - remplir le dôme du parachute principal:
 La quatrième étape
La quatrième étape est une diminution du parachute ouvert:

Compilation d'un système d'équations différentielles pour toutes les étapes d'un saut en parachute
Nous choisissons un système de coordonnées fixes OXY centré au point d'éjection O. L'axe OX coïncide avec la direction de la composante horizontale de la vitesse de l'avion. L'axe OY est dirigé verticalement vers le haut dans la direction opposée à la vitesse verticale du parachutiste.
Nous supposerons que le mouvement du parachutiste est plat et se produit dans le plan OXY. Ce modèle de saut peut être considéré comme un modèle de saut par temps calme sans tenir compte de l'influence du vent.
Nous pensons qu'en plus du poids, le parachutiste est affecté par la force de résistance à l'air proportionnelle au carré de la vitesse du parachutiste:
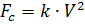
,
où:
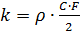
,
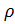
- densité de l'air, C - coefficient de traînée, F - section médiane du corps.
Avec l'augmentation de la hauteur, la température de l'air change:

La température minimale est déjà atteinte à une altitude de 10 km. et est de -55 ° C. La densité de l'air dépend également de la pression. Par conséquent, lors du calcul de la balistique d'un saut en parachute, il est pratique d'utiliser la formule suivante pour déterminer la densité de l'air [1]:
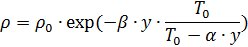
,
où
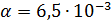
K / m;
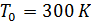
- température au niveau de la mer; y est la hauteur en m;

- densité de l'air à y = 0;
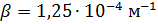
.
Dans la pratique des calculs, le carré de croissance est pris comme section médiane; la valeur de C est trouvée dans le tableau [2]:

Θ désigne l'angle d'inclinaison de la trajectoire. Sous les hypothèses faites pour les composants
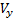
,
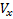
vecteurs de vitesse V nous avons:

Divisant par m les côtés gauche et droit des équations du système résultant et désignant

à travers r, on obtient:
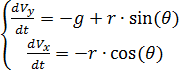
(1)
Nous notons les équations de mouvement d'un parachutiste sous la forme d'un système d'équations différentielles pour les fonctions V, θ, y (t), x (t).
Étant donné que:
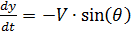
,
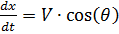
,
et différencier le rapport temporel:

, en tenant compte du système d'équations (1) on obtient:
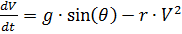
,
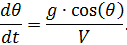
.
Ainsi, dans les conditions initiales:
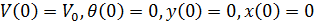
nous avons le système d'équations différentielles suivant:
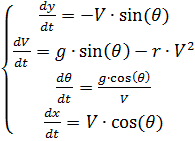
Solution numérique d'un système d'équations différentielles (2) utilisant Python
Pour résoudre (2), nous le réécrivons sous la forme suivante, en introduisant des forces de traînée stabilisantes contrôlées par le temps et la densité de l'air
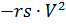
et principal
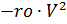
parachutes, respectivement, multipliés par les fonctions de contrôle du temps ks (t) et ko (t):
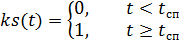
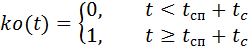
,
où:
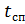
–– temps de chute libre du parachutiste;

- le temps de fonctionnement du parachute de stabilisation jusqu'à l'ouverture du parachute principal.
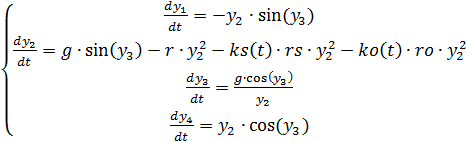
(3)
Liste complète du programme ajusté pour les changements de densité de l'air Nous obtenons:
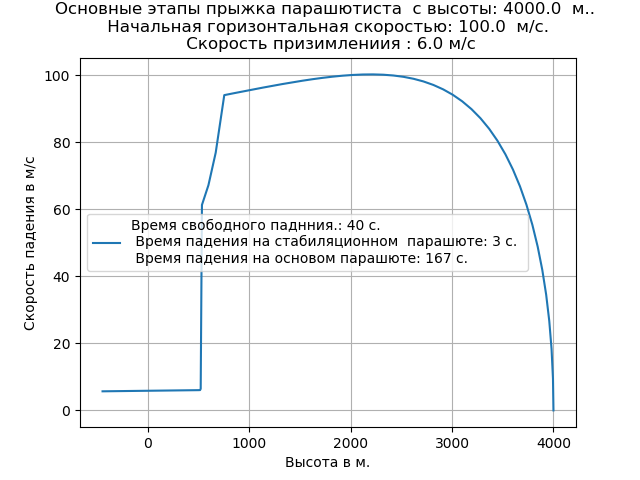
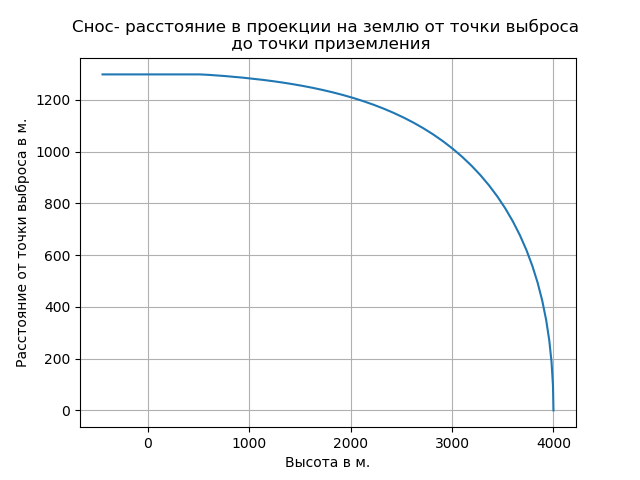
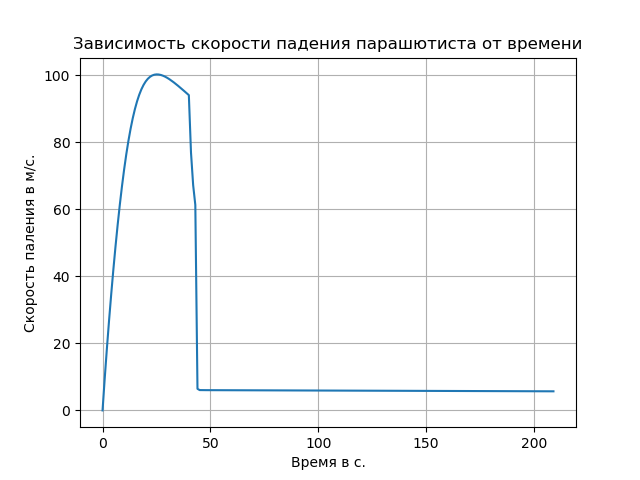
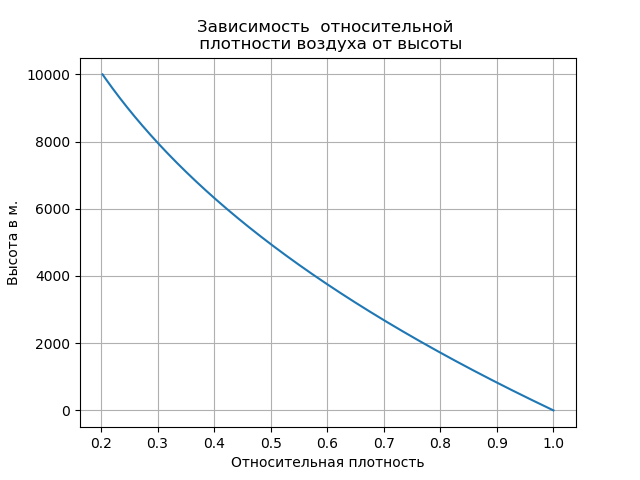
La prise en compte de l'air raréfié a entraîné une augmentation du taux de chute libre et changé la nature de la trajectoire dans cette section.
Ce problème peut être résolu à l'aide d'un système de deux équations différentielles, qui sont données ci-dessous (à l'exclusion des parachutes et des changements de densité de l'air):
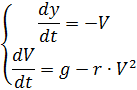
Le changement des forces de résistance et de la densité de l'air est indiqué dans la liste sous le spoiler, en tenant compte de ce qui précède et sans explication# - * - codage: utf8 - * -
à partir de numpy import *
de scipy.integrate import odeint
import matplotlib.pyplot as plt
m = 100
r0 = 1,3
c1 = 0,3
c2 = 0,6
c3 = 0,5
c4 = 0,75
S = 70
s = 0,8
ss = 1,5
g = 9,8
cuillère à café = 6
tsbp = 10
tp = 90,0
h = 1000,0
bêta = 1,25 * 10 ** - 4
alfa = 6,5 * 10 ** - 3
T0 = 300
def ks (t):
si t <tsp:
z = 0
sinon:
z = 1
retourner z
def ko (t):
si t <tsp + tsbp:
z = 0
sinon:
z = 1
retourner z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.title ("Parachutisme de 1000 et 800 mètres")
plt.plot (y1, y2, label = 'Altitude 1000 m')
h = 800,0
cuillère à café = 6
tsbp = 2
tp = 80,0
def ks (t):
si t <tsp:
z = 0
sinon:
z = 1
retourner z
def ko (t):
si t <tsp + tsbp:
z = 0
sinon:
z = 1
retourner z
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.plot (y1, y2, label = 'Hauteur 800 m')
plt.xlabel ('Hauteur en m.')
plt.ylabel ('Vitesse de gravure en m / s.')
plt.legend (loc = 'best')
plt.grid (True)
plt.show ()
Nous obtenons:

Conclusion
Les caractéristiques balistiques et temporelles du mouvement du centre de masse d'un parachutiste atterrissant d'un avion sont déterminées.
Les références
- Pression atmosphérique.
- Gerasimenko I.A. Formation aéroportée: manuel. M .: Military Publishing, 1986. Partie 1, p. 32.