Salut, Habr. Aujourd'hui, je voudrais développer le sujet de l'
optimisation variationnelle et dire comment l'appliquer à la tâche de couper les canaux non informatifs dans les réseaux de neurones (élagage). En l'utilisant, on peut relativement facilement augmenter la «cadence de tir» d'un réseau neuronal sans pelleter son architecture.
L'idée de réduire les éléments redondants dans les algorithmes d'apprentissage automatique n'est pas du tout nouvelle. En fait, il est plus ancien que le concept d'apprentissage en profondeur: ce n'est que plus tôt que les branches d'arbres décisifs ont été coupées et pèsent maintenant dans un réseau de neurones.
L'idée de base est simple: on trouve dans le réseau un sous-ensemble de poids inutiles et on les met à zéro. Sans recherche exhaustive, il est difficile de dire quels poids participent réellement à la prédiction et lesquels ne font que faire semblant, mais ce n'est pas obligatoire. Diverses méthodes de régularisation, Optimal Brain Damage et d'autres algorithmes fonctionnent bien. Pourquoi supprimer tous les poids? Il s'avère que cela améliore la capacité de généralisation du réseau: en règle générale, des poids insignifiants introduisent simplement du bruit dans la prédiction, ou sont spécialement affinés pour détecter les signes d'un ensemble de données d'apprentissage (c'est-à-dire un artefact de recyclage). En ce sens, la réduction des connexions peut être comparée à la méthode de déconnexion des neurones aléatoires (décrochage) lors de la formation du réseau. De plus, si le réseau comporte de nombreux zéros, il occupe moins d'espace dans l'archive et peut lire plus rapidement sur certaines architectures.
Cela semble bien, mais il est beaucoup plus intéressant de jeter non pas des poids séparés, mais des neurones provenant de couches ou de canaux entièrement connectés de l'ensemble des faisceaux. Dans ce cas, l'effet de la compression du réseau et de l'accélération des prévisions est observé beaucoup plus clairement. Mais cela est plus compliqué que de détruire des poids individuels: si vous essayez d'effectuer les dommages cérébraux optimaux, en prenant l'ensemble complet au lieu d'une connexion, les résultats ne seront probablement pas très impressionnants. Afin de pouvoir retirer sans douleur un neurone, il est nécessaire de le faire pour qu'il ne dispose pas d'une seule connexion utile. Pour ce faire, vous devez d'une manière ou d'une autre inciter les neurones «forts» à devenir plus forts et ceux «faibles» à devenir plus faibles. Cette tâche nous est déjà familière: en fait, nous forçons le réseau à induire la rareté avec quelques restrictions sur le regroupement des poids.
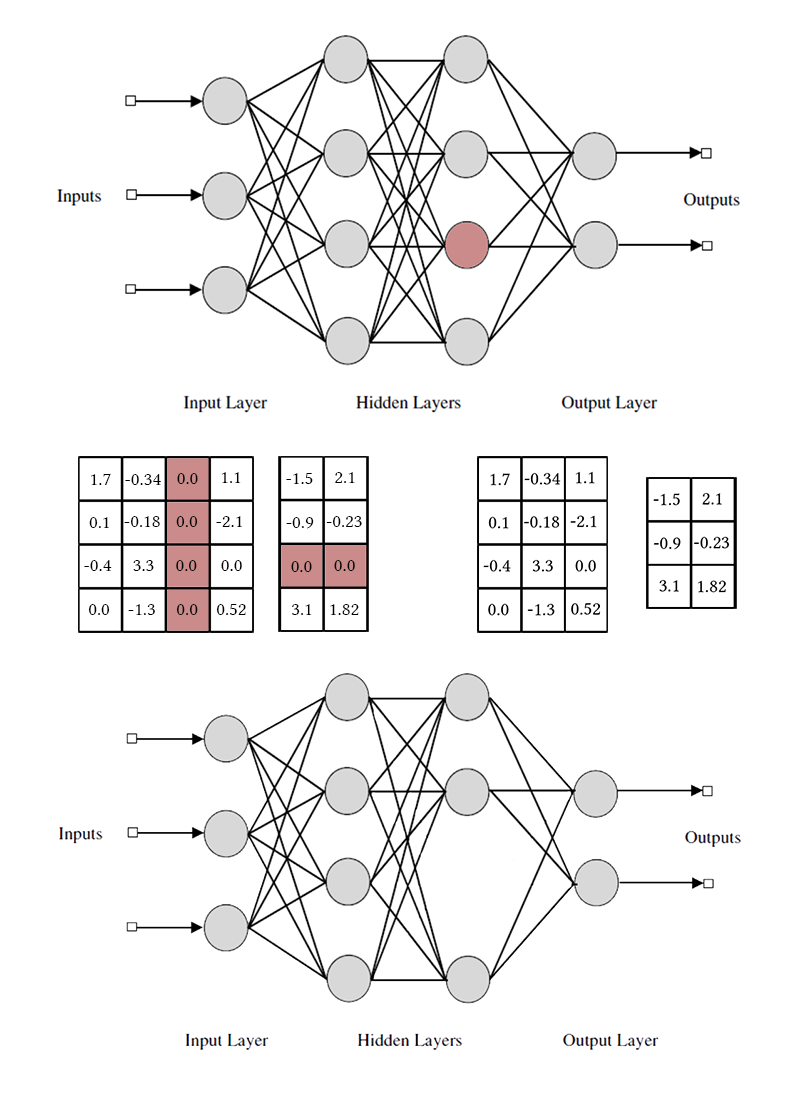
Notez que pour supprimer un neurone ou un canal convolutionnel, vous devez modifier deux matrices de poids. Je ne ferai pas de distinction entre les canaux convolutifs et les neurones: le travail avec eux est le même, seuls les poids spécifiques supprimés et la méthode de transposition diffèrent.
Le plus simple: la régularisation du groupe L1
Pour commencer, je vais vous parler de la manière la plus simple et la plus efficace de supprimer les neurones supplémentaires du réseau - la régularisation de groupe LASSO. Le plus souvent, il est utilisé pour garder des poids inutiles dans les réseaux proches de zéro; il se généralise trivialement au cas par cas. Contrairement à la régularisation régulière, nous ne régularisons pas directement l'activation du poids ou de la couche, l'idée est un peu plus délicate. [Élagage des canaux pour accélérer les réseaux de neurones très profonds; Yihui He et al; 2017]
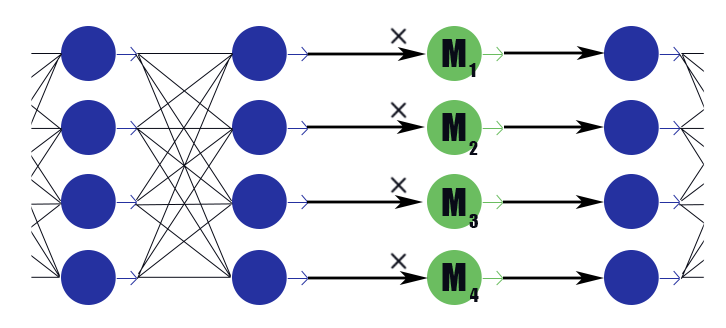
Considérons un calque de masque spécial avec un vecteur de poids
M=( beta1, beta2, dots, betan) . Sa conclusion n'est qu'un travail par morceaux
M aux conclusions de la couche précédente, il n'a pas de fonction d'activation. Nous plaçons dans la couche de masquage après chaque couche, les canaux dans lesquels nous voulons nous débarrasser et soumettons les poids de ces couches à une régularisation L1. Ainsi le poids du masque
betai multiplié par la ième sortie de la couche impose implicitement une restriction sur tous les poids dont dépend cette conclusion. Si parmi ces poids, disons à moitié utiles,
betai restera plus proche de l'unité, et cette conclusion pourra bien transmettre l'information. Mais si seulement un ou aucun,
betai il retombera à zéro, ce qui remettra à zéro la sortie du neurone et, en fait, remettra à zéro tous les poids dont dépend cette conclusion (dans le cas de la fonction d'activation égale à zéro à zéro). Veuillez noter que de cette façon, le réseau reçoit moins de renforcement négatif en cas de poids légalement important ou de réponse juridiquement forte. L'utilité du neurone dans son ensemble est importante.
Il s'avère que cette formule:
O Where
lambda - constante de pondération de loss'a network et loss'a sparseness. Il ressemble à la formule habituelle de régularisation L1, seul le deuxième terme contient des vecteurs de couches de masquage, et non le poids du réseau.
Après l'entraînement du réseau, nous passons en revue les neurones et leurs valeurs de masquage. Si
betai plus d'un certain seuil, alors les poids des neurones sont multipliés par
betai s'il est inférieur, alors les éléments correspondant au neurone sont retirés des matrices des poids entrants et sortants (comme sur l'image un peu plus haut). Après cela, les masques peuvent être supprimés et le réseau terminé.
Dans l'application du groupe LASSO il y a plusieurs subtilités:
- Régularisation normale. Parallèlement à la régularisation des pondérations de masque, la régularisation L1 / L2 doit être appliquée à toutes les autres pondérations du réseau. Sans cela, une diminution du poids de masquage dans le cas de fonctions d'activation insaturées (ReLu, ELu) sera facilement compensée par une augmentation des poids, et l'effet d'annulation ne fonctionnera pas. Oui, et pour les sigmoïdes ordinaires, cela vous permet de mieux démarrer le processus avec une rétroaction positive: Mi la sortie non informative devient plus petite, c'est pourquoi l'optimiseur doit réfléchir plus fortement à chaque poids spécifique, ce qui rend la sortie encore plus non informative, c'est pourquoi Mi diminue encore plus et ainsi de suite.
- Les auteurs de l'article conseillent également d'imposer une restriction sphérique sur le poids des couches |Wi|2=1 . Cela devrait probablement contribuer au «flux» de l'équilibre des neurones faibles aux neurones forts, mais je n'ai pas remarqué de grande différence.
- Entraînement push-pull. Les auteurs de l'article suggèrent de former alternativement les poids normaux du réseau neuronal et les poids de masquage. C'est plus long que d'enseigner tout à la fois, mais comme si les résultats étaient un peu meilleurs?
- N'oubliez pas le long réglage fin du réseau (réglage fin) après la fixation du masque, c'est très important.
- Surveillez attentivement la position de vos masques: avant ou après la fonction d'activation. Vous pouvez avoir des problèmes avec des activations qui ne sont pas égales à zéro lorsque l'argument est nul (par exemple, un sigmoïde).
- L'élagage n'est pas ami avec batchnorm pour la même raison que l'abandon n'est pas ami avec lui: du point de vue de la normalisation, quand il y a 32 valeurs dans le paquet 32 dont 12 sont nulles et quand 20 valeurs dans le paquet sont des situations très différentes. Après avoir arraché la balance mise à zéro, la distribution apprise par la couche batchnorm cesse d'être valide. Vous devez soit insérer des couches d'élagage après toutes les couches batchnorm, soit modifier ces dernières d'une manière ou d'une autre.
- Il existe également des difficultés à appliquer la réduction de canal aux architectures de branchement et aux réseaux résiduels (ResNet). Après avoir coupé des neurones supplémentaires lors de la fusion des branches, les dimensions peuvent ne pas coïncider. Ceci est facilement résolu par l'introduction de couches tampons, dans lesquelles nous ne rejetons pas les neurones. En outre, si les branches du réseau transportent une quantité différente d'informations, il est logique de définir lambda de sorte qu'il ne s'avère pas que l'élagage coupe simplement tous les neurones dans la branche la moins informative. Cependant, si tous les neurones sont coupés, n'est-ce pas une branche si importante?
- Dans l'énoncé initial du problème, il y a une restriction stricte sur le nombre de canaux non nuls, mais à mon avis, il suffit de modifier uniquement les paramètres de pondération de la perte initiale et de la perte L1 des poids de masquage, puis de laisser l'optimiseur décider du nombre de canaux à laisser.
- Capturez des masques. Ce n'est pas dans l'article d'origine, mais à mon avis, c'est un bon mécanisme pratique pour améliorer la convergence. Lorsque la valeur du masque atteint une certaine valeur basse prédéterminée, nous la réinitialisons et interdisons de changer cette partie du masque. Ainsi, les poids faibles cessent complètement de contribuer à la prédiction dès la formation du modèle et n'introduisent aucune valeur parasite dans les quantités correspondantes. Théoriquement, cela peut empêcher un canal potentiellement utile de revenir en service, mais je ne pense pas que cela se produise dans la pratique.
À la dure: régularisation L0
Mais nous ne cherchons pas de moyens faciles, non?
Le rejet de canal utilisant la régularisation L1 n'est pas tout à fait juste. Il permet au canal de se déplacer sur l'échelle de «réponse forte» - «réponse faible» - «réponse zéro». Ce n'est que lorsque le poids de masquage est suffisamment proche de zéro que nous rejetons le canal à l'aide du masque de capture. Un tel mouvement déforme considérablement l'image et modifie les autres canaux pendant l'entraînement: avant de pouvoir apprendre quoi faire lorsque le neurone précédent est complètement éteint, il doit apprendre quoi faire lorsqu'il donne systématiquement une réponse faible.
Permettez-moi de vous rappeler que, idéalement, nous aimerions sélectionner avec impatience le canal le moins informatif du réseau, continuer à apprendre le réseau sans lui, supprimer le canal le moins informatif suivant, ajuster à nouveau le réseau, etc. Hélas, dans une telle formulation, la tâche est insupportable sur le plan des calculs, même pour des réseaux relativement simples. De plus, cette approche ne laisse pas aux canaux une seconde chance - une fois qu'un neurone distant ne peut plus reprendre son fonctionnement. Modifions un peu la tâche: nous allons parfois retirer le neurone, et parfois le laisser. De plus, si le neurone dans son ensemble est utile, il est plus souvent laissé, mais s'il est inutile - inversement. Pour cela, nous utiliserons les mêmes calques de masquage que dans le cas de la régularisation L1 (ce n'est pas sans raison qu'ils ont été introduits!). Seuls leurs poids ne se déplaceront pas le long de l'axe réel entier avec l'attracteur à zéro, mais seront concentrés autour de 0 et 1. Non pas que cela soit devenu beaucoup plus simple, mais au moins réglé le problème de l'élimination catégorique des neurones.
L'instinct du formateur de réseau suggère qu'il ne vaut pas la peine de résoudre le problème par une recherche exhaustive, mais vous devez ajouter à la fonction de perte le nombre de neurones actifs dans les couches en cours d'exécution. Cependant, un tel terme de perte sera constant par étapes et la descente de gradient ne peut pas fonctionner avec lui. Il est nécessaire en quelque sorte d'enseigner l'algorithme d'apprentissage pour exclure périodiquement certains neurones, malgré l'absence de gradient.
Nous avons un moyen de supprimer temporairement les neurones: nous pouvons appliquer un décrochage à la couche de masque. Laisser pendant l'entraînement
betai=1 avec probabilité
pi et
betai=0 avec probabilité
1− pi . Maintenant, dans la fonction de perte, vous pouvez mettre la somme
pi qui est un vrai nombre. Ici, nous sommes confrontés à un autre obstacle: la distribution est discrète, on ne sait pas comment la rétropropagation fonctionne avec elle. En général, il existe des algorithmes d'optimisation spéciaux qui peuvent nous aider ici (voir RENFORCER), mais nous adopterons une approche différente.
C'est là que le moment est venu
où l'optimisation variationnelle entre en
jeu : nous pouvons rendre la distribution discrète des zéros et des uns dans la couche de masquage continue et optimiser les paramètres de cette dernière en utilisant l'algorithme de rétropropagation habituel. C'est l'idée derrière le travail [Apprendre les réseaux de neurones clairsemés par la régularisation L0; Christos Louizos et al; 2017].
Le rôle de la distribution continue sera joué par la distribution de béton dur [The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables; Chris Maddison; 2017], voici une chose si délicate à partir des logarithmes qui se rapproche de la distribution de Bernoulli:
alpha - répartition décalée par rapport au centre, et
beta - la température. À
beta rightarrow0 la distribution commence de plus en plus à se rapprocher de la vraie distribution de Bernoulli, mais perd sa différentiabilité. À
0< beta<1 la densité de distribution est concave (c'est le cas qui nous intéresse), par
beta>1 - convexe. Nous passons cette distribution à travers un sigmoïde rigide afin qu'il puisse habilement donner avec une probabilité non nulle finie
z=0 et
z=1 , et sur l'intervalle (0, 1), il avait une densité différenciable continue. Après avoir terminé l'élagage, nous regardons dans quelle direction la distribution s'est déplacée et remplaçons la variable aléatoire
z à une valeur de masque spécifique
beta et nous apportons à la condition un modèle déjà déterministe.
Pour ressentir une distribution un peu meilleure, je vais donner quelques exemples de sa densité pour différents paramètres:
Densité de distribution a l p h a = 0,0 , b e t a = 0,8 :
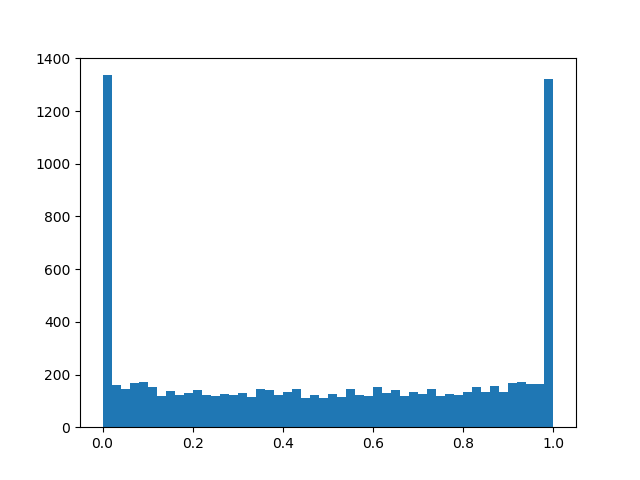 a l p h a = 1,0 , b e t a = 0,8
a l p h a = 1,0 , b e t a = 0,8 :
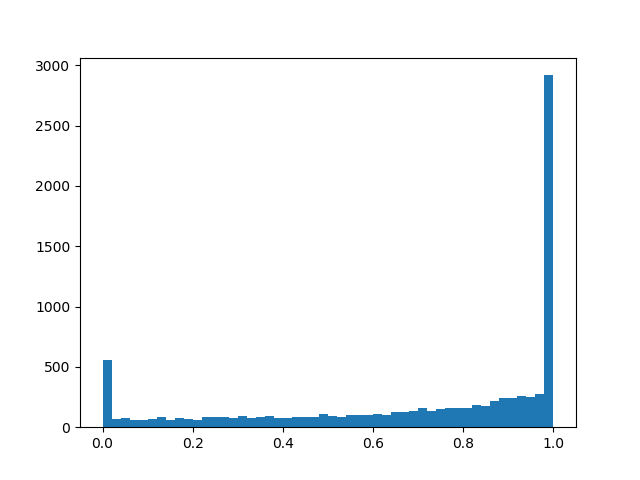 alpha=2.0, beta=0.8
alpha=2.0, beta=0.8 :
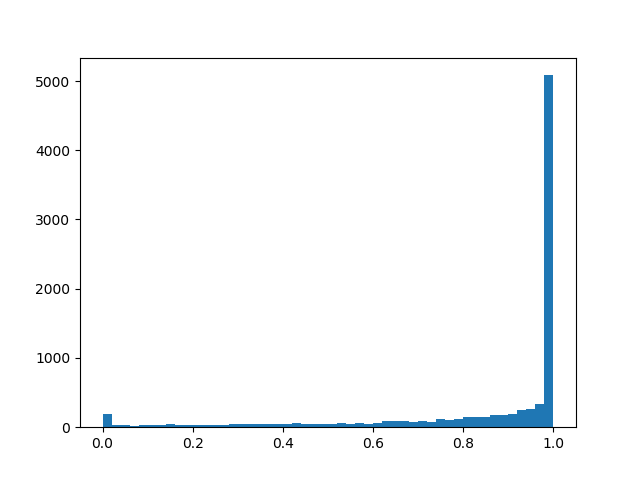 alpha=0,0, beta=0,5
alpha=0,0, beta=0,5 :
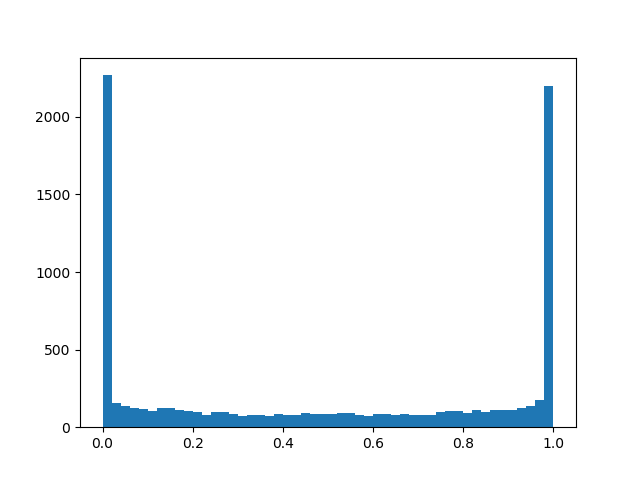 alpha=1.0, beta=0.5
alpha=1.0, beta=0.5 :
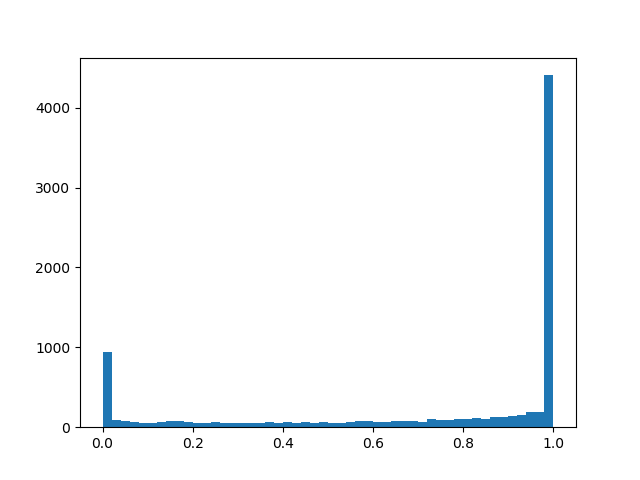 alpha=2.0, beta=0.5
alpha=2.0, beta=0.5 :
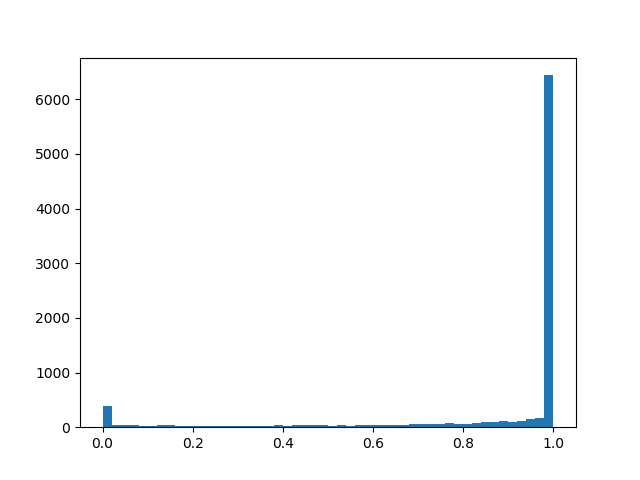 alpha=2.0, beta=0.1
alpha=2.0, beta=0.1 :
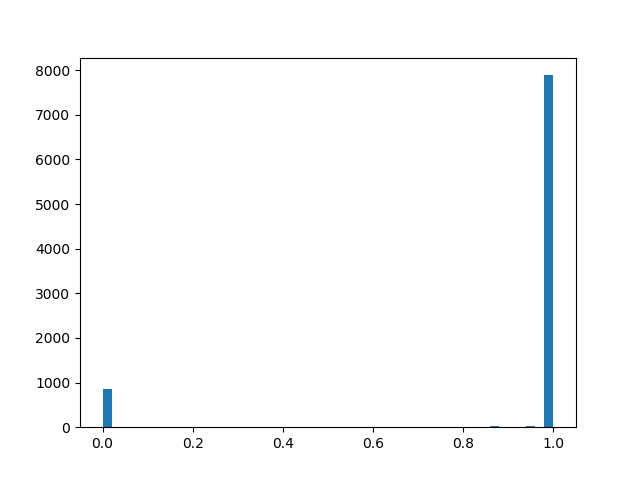 a l p h a = 2,0 , b eta=2.0
a l p h a = 2,0 , b eta=2.0 :
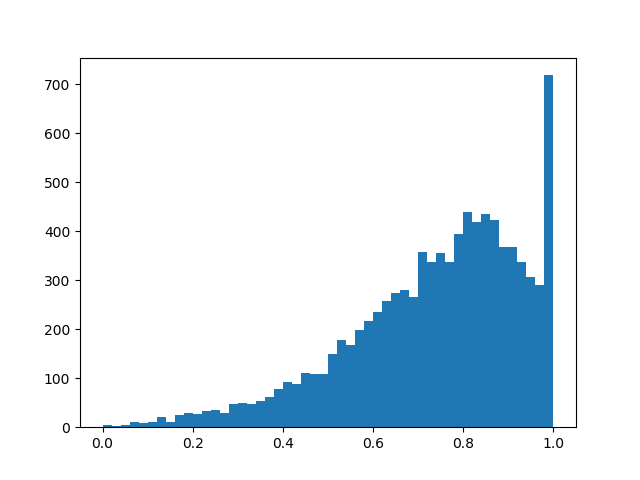
Essentiellement, nous avons une couche d'abandon «intelligente» qui apprend quelles conclusions devraient être jetées plus souvent. Mais qu'optimisons-nous exactement? En cas de perte, vous devez placer l'intégrale de la densité de distribution dans une région non nulle (la probabilité que le masque se révèle non nul pendant l'entraînement, mettez simplement):
Les fonctionnalités suivantes sont ajoutées à la formation push-pull, à la régularisation régulière et aux autres détails de mise en œuvre mentionnés dans le chapitre sur la régularisation L1:
- Encore une fois: notre couche d'abandon «intelligent» avec une probabilité notable réinitialise la sortie, avec certains - la laisse telle quelle, et en plus, il y a une petite chance selon beta, xi, gamma que la sortie sera multipliée par un nombre aléatoire de 0 à 1. La dernière partie est plus parasite qu'utile pour notre objectif final, mais sans elle en aucune façon - elle est nécessaire pour la rétro-propagation.
- Généralement et alpha et beta - paramètres de formation, mais dans mes expériences, j'ai senti que si vous demandez juste un peu beta (0,05) et dans le processus d'apprentissage, il est toujours réduit linéairement, l'algorithme converge mieux que si vous l'apprenez honnêtement. alpha il vaut mieux régler assez grand log alpha environ2,5 de sorte qu'au départ les neurones sont plus souvent préservés que jetés, mais pas assez gros pour saturer le sigmoïde en perte.
- En cas de remplacement dans les formules log alpha juste alpha comme si le réseau convergeait mieux et était moins susceptible de tomber sur NaN pendant la formation. Avec cette manœuvre, il ne faut pas oublier de changer le terme dans la fonction de perte et d'initialisation.
- De plus, si vous trichez et remplacez le sigmoïde habituel dans loss'e par un rigide avec des restrictions sur log alpha in[−4,4] , la régularisation convergera mieux et agira plus fort.
- À alpha et beta Vous pouvez également appliquer la régularisation pour augmenter encore la rareté.
- Après la formation, vous devez binariser les résultats et entraîner de manière persistante le réseau avec le masque déterminé jusqu'à ce que la précision val atteigne la constante. L'article fournit une formule plus précise grâce à laquelle la sortie d'un neurone peut être rendue déterministe lors de la validation ou de la libération d'un réseau pour la libération, mais il semble qu'à la fin de la formation alpha s'avérer suffisamment polarisé pour qu'une simple heuristique fonctionne: alpha<0 - masque 0, alpha geq0 - masque 1 (mais ce n'est pas précis). Après être passé à des masques déterministes, vous verrez un saut de qualité. N'oubliez pas que nous sommes arrivés ici à zéro poids, et en dessous d'un certain seuil de poids, vous devez toujours remplacer les poids de masquage par des zéros.
- Un avantage supplémentaire de l'approche L0 - les couches de masquage commencent à fonctionner comme un décrochage, ce qui apporte un puissant effet de régularisation au réseau. Mais c'est une arme à double tranchant: si vous commencez à vous entraîner avec trop peu alpha Il existe un risque de ruiner la structure du réseau pré-formé.
Les expériences
Pour l'expérience, prenez l'ensemble de données CIFAR-10 et un réseau relativement simple de quatre couches convolutionnelles, suivies de deux entièrement connectées: Conv2D, Mask, Conv2D, Mask, Pool2D, Conv2D, Mask, Conv2D, Mask, Pool2D, Flatten, Dropout (p = 0,5) , Dense, Mask, Dense (logits). On pense que les algorithmes d'élagage fonctionnent mieux sur des réseaux plus épais, mais ici je suis tombé sur un problème purement technique de manque de puissance de calcul. En tant qu'optimiseur, Adam a été utilisé avec un taux d'apprentissage = 0,0015 et une taille de lot = 32. De plus, les régularisations habituelles L1 (0,00005) et L2 (0,00025) ont été utilisées. L'augmentation d'image n'a pas été appliquée. Le réseau a été formé 200 époques avant la convergence, après quoi il a été préservé, et des algorithmes de réduction des neurones lui ont été appliqués.
En plus d'appliquer les algorithmes décrits ci-dessus pour l'élagage, nous avons défini un point de référence trivial pour nous assurer que les algorithmes font quelque chose. Essayons de jeter le premier de chaque couche
k les neurones et terminer le réseau résultant.
Le graphique montre les résultats de la comparaison des algorithmes de réduction des canaux L1 et L0 après une série d'expériences avec différentes constantes de puissance de régularisation. L'axe des x
représente le pourcentage de réduction du nombre de
poids après application de l'algorithme. Sur l'axe Y, la précision du réseau coupé dans l'échantillon de validation. La barre bleue au milieu représente la qualité approximative d'un réseau qui n'a pas encore été coupé de neurones. La ligne verte représente un simple algorithme d'apprentissage du masque L1. La ligne rouge est la taille L0. Ligne violette - premier retrait
k canaux. Triangles noirs - formation d'un réseau qui avait initialement moins de poids.
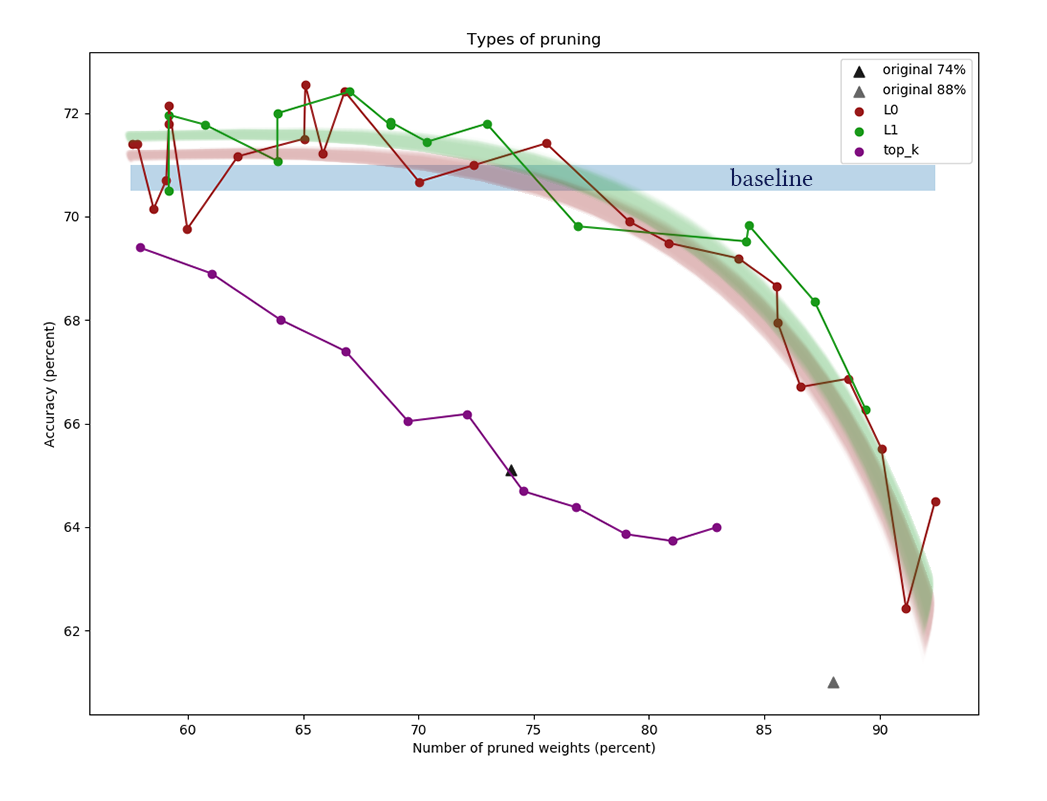
Un autre exemple pour le CIFAR-100 et un réseau légèrement plus long et plus large d'environ la même architecture et avec des paramètres de formation similaires:
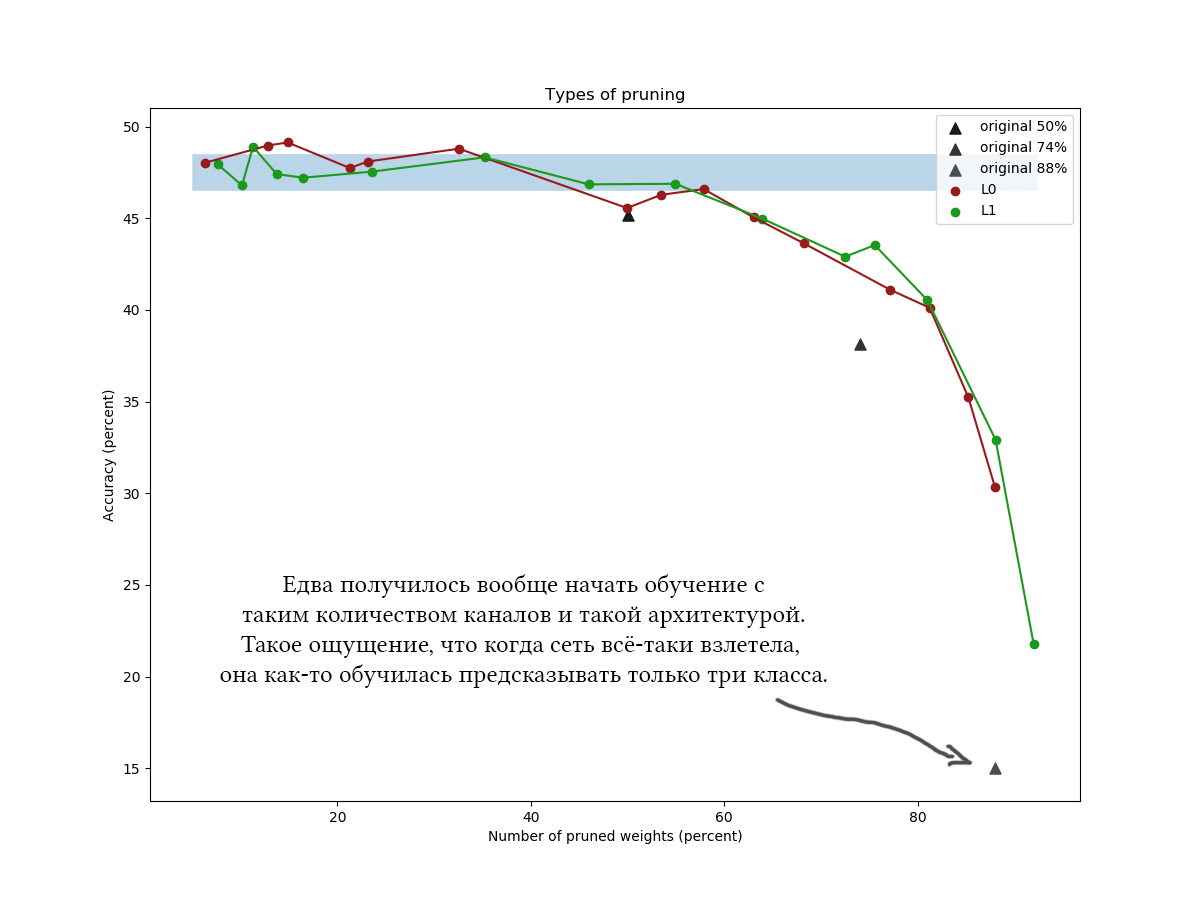
Dans les graphiques, il est clairement visible qu'un simple algorithme L1 ne fait pas pire que l'optimisation variationnelle astucieuse, et il semble qu'il améliore même un peu plus la qualité du réseau à de faibles valeurs de compression. Les résultats sont également confirmés par des expériences ponctuelles avec d'autres ensembles de données et architectures de réseau. C'est un résultat absolument attendu, sur lequel je comptais lorsque j'ai commencé des expériences sur la réduction de réseau. Honnêtement. Soupir.
Eh bien, pour être honnête, j'ai été un peu surpris, et j'ai essayé de jouer avec l'algorithme et le réseau: différentes architectures, hyperparamètres de réseau, formules exactes de distribution en béton dur, valeurs initiales
alpha et
beta , le nombre d'époques de réglage intermédiaire. La régularisation L0 semble cool en théorie, mais en pratique, il est plus difficile de détecter les hyperparamètres, et cela prend plus de temps, donc je ne recommanderais pas de l'utiliser sans expériences supplémentaires et traitement de fichier. Veuillez ne pas tenir compte du temps passé à lire l'article: l'élagage L0 semble vraiment très crédible, et je dirais que j'ai plutôt appliqué l'algorithme quelque part incorrectement, que je n'ai pas reçu le gain promis. De plus, l'optimisation variationnelle est la base d'algorithmes de réduction encore plus avancés [par exemple, la compression de réseaux de neurones à l'aide de la variationnelle
Goulot d'étranglement de l'information, 2018].En général, les conclusions suivantes peuvent être tirées:- De nombreux canaux du réseau formé sont clairement redondants. Même si vous définissez une constante de régularisation de petit masque, il est facile d'obtenir une réduction de 30 à 50% des poids. Mais si vous vous entraînez initialement sur une grille trop fine, il est difficile d'obtenir de bons résultats. Cela parle en faveur de l'effet bénéfique de larges couches sur la fonction cible du réseau et en faveur de la théorie des billets de loterie [The Lottery Ticket Hypothesis: Training Pruned Neural Networks, J. Frankle et M. Carbin, 2018] (plus il y a de neurones, plus il est probable que, bien que si l'un d'eux est initialisé pour qu'il forme une bonne règle).
- , . . , ?
- , . 60-90% . k <7%, .
- , (<60%) : , !
- L1 L0 (APoZ), , .. , k .
- , . , , , , . , , . pruning' , . - , .
Rappelez-vous comment j'ai écrit au début du post qu'après avoir terminé l'algorithme d'élagage, vous pouvez "couper complètement les éléments supplémentaires du réseau"? Donc, couper des morceaux supplémentaires du réseau n'est pas du tout facile. Tensorflow et d'autres bibliothèques construisent un graphe de calcul, et il ne peut pas être modifié si facilement lorsqu'il est déjà en fonctionnement. Vous devez enregistrer le réseau avec les masques calculés, en détacher la liste des poids nécessaires, transposer les poids selon les besoins, supprimer les groupes mis à zéro, transposer en arrière et créer un nouveau réseau basé sur l'ensemble de sortie des tenseurs. Le réseau résultant devrait avoir la même configuration que l'original, mais il aura moins de neurones. Attendez-vous à un mal de tête en conservant le même schéma de réseau dans la fonction de création du réseau initial et final, surtout s'ils ne sont pas linéaires, mais branchés.Pour un masquage pratique, vous devez probablement créer vos propres calques. C'est facile, mais faites attention aux collections auxquelles vous ajoutez des options de masquage. Il est facile de faire une erreur et d'entraîner accidentellement les paramètres de réduction de canal avec toutes les autres échelles.Il convient de noter qu'une partie importante des poids des réseaux avec des architectures peu profondes est généralement concentrée sur la transition d'une partie convolutionnelle à une partie entièrement connectée. Cela est dû au fait que la dernière couche convolutionnelle est rendue plate, à la suite de quoi, pour ainsi dire, le (nombre de canaux) * (largeur) * (hauteur) des neurones s'y forme et la matrice de poids suivante est très large. Il est peu probable que ces poids soient réduits; de plus, cela ne doit pas être fait, sinon les dernières couches du réseau seront «aveugles» aux fonctionnalités trouvées à certains endroits. Dans de tels cas, essayez de réduire le nombre final de canaux et d'utiliser maxpool'ing ou même d'utiliser des architectures entièrement convolutives ou entièrement connectées.Merci à tous pour votre attention, si quelqu'un souhaite répéter les expériences sur le CIFAR-10 et le CIFAR-100,le code peut être pris sur github . Bonne journée de travail!