Présentation

Cette courte note expliquera comment le modèle de diffusion de la lumière atmosphérique est structuré dans notre dernier 4k int Appear by Jetlag , dont la version fête a remporté une honorable 12e place dans l'intro compo 4k lors de la soirée de démonstration Revision 2018 en avril de cette année.

Vous pouvez télécharger le binaire gratuitement sans SMS ici .

Si, cependant, vous n'avez pas Windows, ou si vous n'avez pas de puissante carte vidéo moderne, alors il y a un idiot réconfortant:

La musique de cette œuvre a été écrite par vif en utilisant 4klang . Tout le code et les visuels sont restés derrière moi.

Ici, nous ne parlerons que du modèle de diffusion de la lumière. D'autres choses, telles que les outils, un modèle de ville, un modèle d'éclairage et de matériaux, ne sont pas affectées. Je peux envoyer les courageux lire la source ou regarder les enregistrements de la façon dont je me noie depuis des heures - l'essentiel du développement a été en vidéo.

Une histoire ennuyeuse à manquer

Le travail sur ce travail a commencé avec la prise de conscience que le principal travail à temps plein ne laisse pas le temps de travailler sur un travail à part entière en 4k - c'est déjà presque la mi-mars dans la cour, il reste quelques semaines avant Revizen.
Il ne reste plus qu'à trouver quelque chose d'assez simple pour un remplissage rapide, pour quelques soirées, de compo. Faire une autre marche stupide n'est pas respecter le spectateur, alors je me suis souvenu qu'il y a quelques années, je devais faire un shader avec dispersion, et c'était assez simple, compact et en même temps beau, mais assez lent.

Au cours d'une brève discussion, j'ai insisté de mon côté et nous avons décidé de nous concentrer sur ce qui suit: faire un paysage rempli de lumière diffuse, avec coucher de soleil, nuages et rayons crépusculaires (TIL comme l'expression "rayons divins" est traduite). Afin de ne pas élever le nombre de marches dans l'atmosphère à des valeurs complètement non interactives, vous devez fortement vibrer (une telle méthode de la cour de Monte Carlo), ce qui générera du bruit visible. Mais peu importe si vous déplacez la caméra et modifiez la scène lentement et que vous démarrez la piste ambiante, vous pouvez mélanger sans douleur les images adjacentes et atténuer temporairement ce bruit.

Keen a écrit la musique assez rapidement - elle était presque prête deux semaines avant la révision. Cependant, j'étais gravement paralysé par la grippe - avec une ambulance et une maladie infectieuse - alors je n'ai pratiquement commencé à travailler sur le shader qu'au moment où, dans des conditions de vie plus ou moins importantes, j'ai pris l'avion pour Francfort. Le prototype de ce modèle de diffusion était déjà écrit dans les airs.

Nous avions déjà fouetté la version Party de l'intra à partir du sable et de la salive lors de la fête elle-même pendant les quelques heures restantes avant la date limite (et, probablement, quelques après; D), alors que je m'éloignais simultanément de la grippe, du manque de sommeil, des vols de plusieurs heures et il a été constamment distrait en participant à la compo de livecoding Shader showdown .

La version présentée sur grand écran contenait beaucoup d'artefacts et seulement la géométrie rudimentaire de la ville basée sur le diagramme de Voronoi avec des hauteurs aléatoires.

En général, la 12e place est assez généreuse.

La version finale, illustrée ci-dessus, a été réalisée plus tard et dans un mode plus détendu, de 1 à 2 heures du soir par semaine pendant un mois. Au total, il a fallu environ 40 à 50 heures de travail pour travailler.

Modèle de diffusion

(Remarque: je ne fais pas de programmation graphique professionnelle. C'est mon petit passe-temps confortable pour le bien, si cent ou deux sont très défocalisés sous ~~la bière~~ heures de vin par an. Par conséquent, il n'y a aucune probabilité nulle que certaines choses soient décrites ci-dessous et / ou nommées de manière incorrecte. Mon oncle, frappe!)

Le modèle de diffusion est emprunté à l'article "High Performance Outdoor Light Scattering Using Epipolar Sampling" par Egor Yusov , publié dans le livre GPU Pro 5 , avec un échantillonnage épipolaire complètement éjecté.

Modèle physique

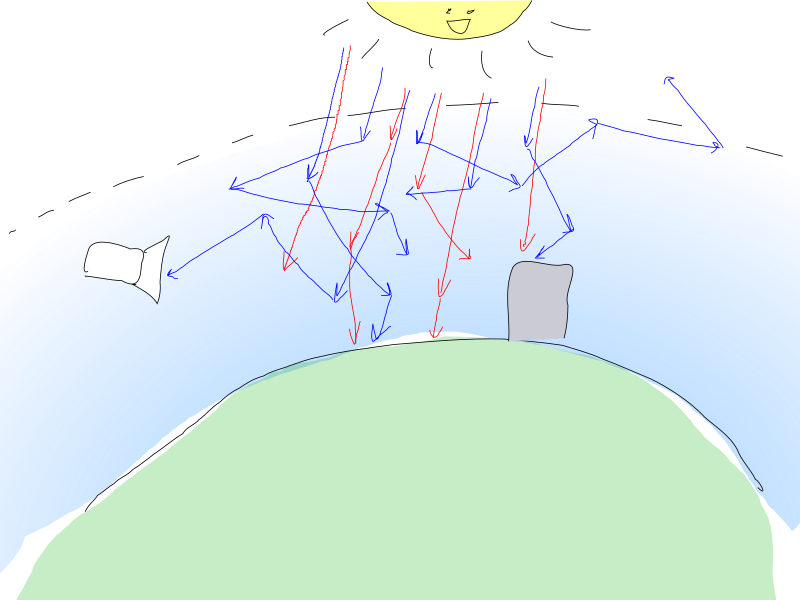
Les photons du soleil bombardent l'atmosphère terrestre et interagissent avec les particules d'air. Un photon peut être diffusé par une particule, ce qui entraîne un changement de direction du photon, ou il peut être absorbé, ce qui signifie que le photon est perdu et que son énergie a été convertie sous une autre forme.
Les deux processus sont probabilistes et dépendent notamment de la densité des particules et de l'énergie photonique (qui correspond à sa couleur).

Sur les doigts, les photons «rouges» ont moins de chances d'interagir avec l'air, ils surmontent donc l'épaisseur de l'atmosphère relativement intacte.
Les bleus, cependant, ont une probabilité de diffusion plus élevée, c'est pourquoi ils peuvent changer de direction à plusieurs reprises et parcourir des distances considérables dans l'atmosphère avant d'atteindre (ou non) l'observateur.

Les paramètres de l'interaction de la lumière avec l'air qui nous intéressent sont les suivants:

$\ beta ^ s (x)$ - fraction de lumière diffusée par unité de longueur en un point $x$
$\ beta ^ a (x)$ - fraction de lumière absorbée par unité de longueur en un point $x$
$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$ - fraction totale de lumière perdue par unité de longueur en un point $x$
$p (\ alpha)$ Est la distribution angulaire de la lumière diffusée, où $\ alpha$ c'est l'angle entre le faisceau incident et le faisceau diffusé

On suppose que l'air se compose de deux types de particules dont la diffusion se produit indépendamment: les molécules (modèle de Rayleigh) et les aérosols (particules sphériques relativement grandes, diffusion Mie dans la littérature de langue anglaise). Les modèles ne diffèrent que par des valeurs différentes pour les paramètres ci-dessus.

Pour les deux modèles, on pense que la densité des particules correspondantes diminue de façon exponentielle avec la hauteur: $\ rho = \ rho_0e ^ {- \ frac {h} {H}}$ où $\ rho_0$ - densité au niveau de la mer. Cotes $\ beta$ proportionnelle $\ rho$ , et leurs significations ci-dessous sont données pour niveau de la mer.

Modèle Rayleigh

$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$ [Nishita et al. 93, Preetham et al. 99]
$\ beta_R ^ a = 0$
$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$ [Riley et coll. 04, Bruneton et Neyret 08]
$H_R = 7994m$ [Nishita et al. 93]

Aérosols

$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alpha)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$ [Nisita et al. 93, Riley et al. 04] où $g = 0,76$ [Bruneton et Neyret 08]
$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$ [Bruneton et Neyret 08]
$\ beta_M ^ e = 1.1 \ beta_M ^ s$
$H_M = 1200m$ [Nishita et al. 93]

Approximation de diffusion unique

L'approximation de diffusion est basée sur l'émission d'un faisceau de chaque pixel de la caméra et sur le calcul de la quantité de lumière de l'atmosphère qui devrait provenir de cette direction. Chaque rayon correspond aux trois composantes de la lumière RVB, comme si trois photons aux énergies correspondantes volaient le long de ce rayon.

La lumière atteignant la chambre est formée par les processus suivants dans l'air:

Diffusion (TIL que les figues apprennent à traduire en diffusion). La lumière émise par le soleil est ajoutée, qui est diffusée de manière probabiliste par un angle correspondant à la direction de la caméra.
Absorption . La lumière qui vole déjà le long du faisceau est absorbée par l'air.
Diffusion . La lumière qui vole déjà le long du faisceau est perdue pour se diffuser dans d'autres directions.

Pour des raisons de performances, nous pensons que la lumière ne peut entrer dans la direction de la caméra qu'en se diffusant une fois et que toute autre lumière (qui a été diffusée plusieurs fois) peut être négligée. Ce n'est pas recommandé pour le crépuscule, mais que faire.

Cette approche est représentée dans la belle image suivante (j'ai essayé!):

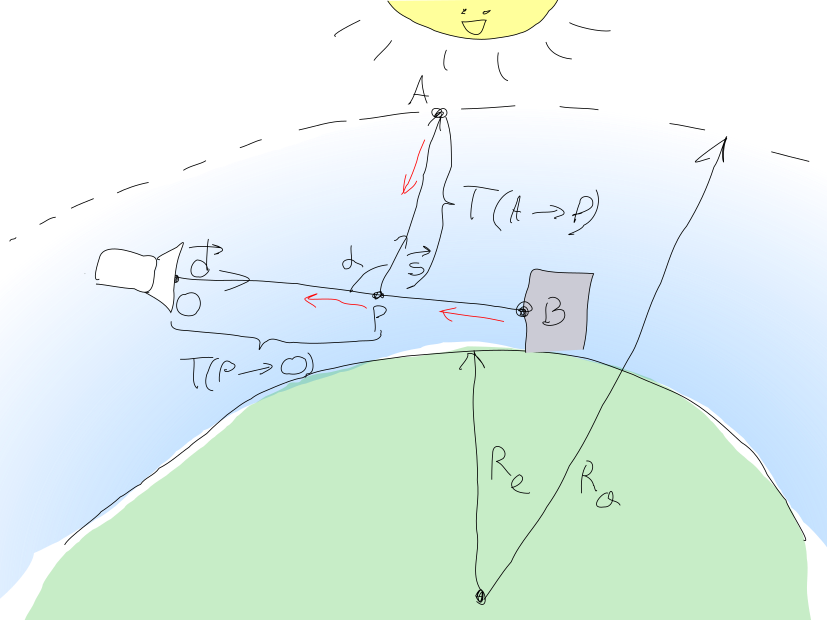
Ainsi, la quantité de lumière qui doit être détectée par le pixel de la caméra à $O$ peut être calculé comme la somme $\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$ où $\ mathbf {L_ {in}}$ - la lumière diffuse du soleil, et $\ mathbf {L_ {BO}}$ - la quantité de lumière du point $B$ scène de géométrie d'objet atteignant $O$ .

Géométrie légère

$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$ où $\ mathbf {L_O}$ La lumière émise d'un point $B$ vers la caméra.

$\ mathbf {T} (B \ rightarrow O)$ appelé l' épaisseur optique du milieu entre les points $B$ et $O$ et est calculé comme suit:

m a t h b f T (B r i g h t a r r o w O) = i n t_{B}^{O} (b e t a_{M}^{e} (s) + m a t h b f b e t a_{R}^{e} (s)) d s

$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$

Attendu que les membres $\ beta$ se composent d'une densité constante et variable du niveau de la mer, cette expression peut être convertie en:

m a t h b f T (B r i g h t a r r o w O) = b e t a_{M}^{e} c d o t i n t_{B}^{O} r h o_{M} (s) d s + m a t h b f b e t a_{R}^{e} i n t_{B}^{O} r h o_{R} (s) d s = b a r m a t h b f b e t a c d o t b a r T_{} r h o (B r i g h t a r r o w O)

$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$

Veuillez noter que je ne divulgue pas spécifiquement $\ rho$ , car nous les modifierons plus tard lors de l'ajout de nuages. J'attire également l'attention sur le fait que $\ beta$ - Vecteurs RVB (au moins $\ mathbf {\ beta_R}$ ont des significations différentes pour les composants RVB, et $\ beta_M$ - vecteur juste pour la cohérence). Membres avec $\ rho$ sous l'intégrale sont des scalaires.

Soleil

Soleil $\ mathbf {L_ {in}}$ calculé par intégration sur tous les points $P$ le long du segment $Ob$ et l'accumulation de toute la lumière solaire entrante se dispersant vers la caméra et mourant dans l'épaisseur $\ mathbf {T} (P \ rightarrow O)$ .

La quantité de lumière solaire atteignant un point $P$ est calculé par une formule similaire $\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$ où $\ mathbf {L_ {sun}}$ - l'éclat du soleil, et $A$ Est le point auquel le rayon du point $P$ vers le soleil $\ vec {s}$ quitte l'atmosphère. La fraction de cette lumière qui sera diffusée vers la caméra est $\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$ .

Total nous obtenons:

m a t h b f L_{i n} = i n t_{B}^{O} m a t h b f L_{P} (s) c d o t (b e t a_{M}^{s} (s) p_{M} (a l p h a) + m a t h b f b e t a_{R}^{s} (s) p_{R} (a l p h a)) c d o t e^{- m a t h b f T (P (s) r i g h t a r r o w O)} d s

$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$

Vous remarquerez peut-être que:

$\ alpha$ est une constante pour chaque pixel-rayon de la caméra (nous pensons que le soleil est infiniment loin et que les rayons qui en proviennent sont parallèles)
Cotes $\ beta$ composé à la fois de constantes du niveau de la mer et de fonctions de densité $\ rho (s)$
Les fonctions $p (\ alpha)$ ont des facteurs communs pour les deux processus de diffusion

Cela vous permet de convertir l'expression en:

m a t h b f L_{i n} = m a t h b f L_{s u n} (1 + c o s^{2} (a l p h a)) (f r a c f r a c 1 4 p i f r a c 3 (1 - g^{2}) 2 (2 + g^{2}) (1 + g^{2} - 2 g c o s (a l p h a))^{} f r a c 32 b e t a_{M}^{s} c d o t m a t h b f I_{M} + f r a c 3 16 p i m a t h b f b e t a_{R}^{s} c d o t m a t h b f I_{R})

$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$

où

m a t h b f I_{M} = i n t_{B}^{O} r h o_{M} (s) e^{- m a t h b f T (A r i g h t a r r o w P (s)) - m a t h b f T (P (s) r i g h t a r r o w O)} d s

$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$

m a t h b f I_{R} = i n t_{B}^{O} r h o_{R} (s) e^{- m a t h b f T (A r i g h t a r r o w P (s)) - m a t h b f T (P (s) r i g h t a r r o w O)} d s

$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$

$I_m$ et $I_R$ ne diffèrent que par les fonctions de densité; leurs exponentielles sont les mêmes.

Personne n'a été en mesure de calculer ces intégrales de manière analytique, donc elles doivent être calculées numériquement en utilisant le remappage (comme on dit dans les publications originales, vous ne pouvez pas le faire!)

Intégration numérique

Pour des raisons de taille et de paresse, nous la considérerons comme la plus stupide possible: $\ int_A ^ B f (x) dx \ approx \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

La marche des rayons sera effectuée dans la direction opposée au flux lumineux: du point de la caméra $O$ avant l'intersection de la poutre avec la géométrie $B$ . Segment de ligne $O \ rightarrow B$ divisé par $N$ étapes.

Avant de commencer la marche, initialisez les variables:

vec2 (deux composants séparés, pour Rayleigh et la diffusion des aérosols) épaisseur optique totale accumulée $\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
vec3 (RVB) $\ mathbf {I_M}$ , $\ mathbf {I_R}$

Suivant pour le point $P_i$ chaque étape entre $O$ et $B$ :

Rayons $\ vec {s}$ en direction du soleil et marquer un point $A_i$ la sortie de ce rayon de l'atmosphère.
Calculez l'épaisseur $\ mathbf {T} (A \ rightarrow P_i)$ en calculant d'abord $\ int_A ^ {P_i} \ rho_M (s) ds$ et $\ int_A ^ {P_i} \ rho_R (s) ds$ en utilisant la même re-marche (avec le nombre d'étapes M ), puis multipliez les termes résultants par les constantes correspondantes $\ beta_M ^ e$ et $\ mathbf {\ beta_R ^ e}$ .
Calculez l'épaisseur $\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
Accumuler $\ mathbf {I_R}$ et $\ mathbf {I_M}$ en utilisant ces valeurs

La couleur finale après réarchivage est calculée par la somme des termes:

Durée $\ mathbf {L_ {BO}}$ devenir trivial: une variable contenant $\ mathbf {T_ \ rho} (P_i \ rightarrow O)$ contient de la valeur $\ mathbf {T_ \ rho} (B \ rightarrow O)$ depuis $P_i$ a atteint $B$ .
Par multiplication $\ mathbf {I_R}$ et $\ mathbf {I_M}$ aux constantes correspondantes et en ajoutant le résultat est calculé $\ mathbf {L_ {in}}$

Shaders

Diffusion simple sans personne

Légèrement peigné et commenté les sources de diffusion prises (presque) directement de l'intra lui-même:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); }

Tais-toi sur le shader

Les nuages

Pas mal, mais une telle image pourrait également être obtenue beaucoup plus facilement avec une pile de dégradés rusée.

De manière trompeuse, obtenir des nuages et des rayons divins est beaucoup plus difficile. Ajoutons.

L'idée est d'approximer les nuages avec des aérosols et de ne modifier que les densités de fonctions de densité densitiesRM() . Cela peut ne pas être aussi correct physiquement que nous le souhaiterions (je n'ai aucune idée de la façon dont la diffusion de la lumière dans les nuages dans l'infographie s'approche réellement).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; }

Contrairement aux attentes, nous n'obtenons pas de beaux nuages, une douce victoire et des fans, mais des artefacts. Essayer d'augmenter le nombre d'étapes des artefacts sur le front ne supprime pas complètement, mais gâche considérablement les performances.

~~Des solutions~~ béquilles qui poussent l'intra:

Les artefacts les plus désagréables à l'horizon se cachent derrière les montagnes
Les nuages sont ajoutés uniquement près de la caméra.
Monte-Karlovschina est ajoutée, chaque rayon de marche est décalé d'un décalage aléatoire: for (float i = pixel_random.w; i < steps; ++i) . Cela ajoute au bruit même que vous devez atténuer temporairement en mélangeant des images successives.

Le nombre d'étapes pour les zones nécessitant plus de détails augmente (par exemple, une couche avec des nuages). C'est pour cela qu'une telle séparation absurde des fonctions en scatterImpl() et scatterDepthInt() :

 //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.);

 //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); }

Alignement avec la géométrie de la scène

Grâce au remappage traditionnel des fonctions de distance et d'ombre, la distance L au point B et la couleur de pixel Lo ont déjà été obtenues. Ces valeurs sont simplement substituées dans la fonction scatter() . Si le faisceau ne repose pas contre la géométrie et quitte la scène, alors la couleur Lo nulle et L calculé en utilisant escape() - on pense que le faisceau a quitté l'atmosphère.

Comme tout.

... En fait, bien sûr, pas tous. C’est assez pénible de frotter toutes les parties ensemble pour que l’ensemble semble crédible. Juste un tas d'agitation avec des paramètres de torsion, la géométrie de la scène, les fonctions de bruit, la trajectoire et l'angle de la caméra. J'ai bien peur de ne pas avoir de bons conseils ici, sauf pour répéter sur plusieurs heures et me cogner la tête contre le mur.

Minification

Après avoir traité le minificateur de shader , le code de dispersion du shader final a une taille d'environ 1500 octets. Crinkler le comprime à ~ 700 octets, ce qui représente environ 30% de tout le code du shader.

Elevage

Je ne sais pas comment faire de l'infographie.

Diffusion de la lumière atmosphérique en moins de quatre kilo-octets