Modèle de régression polynomiale

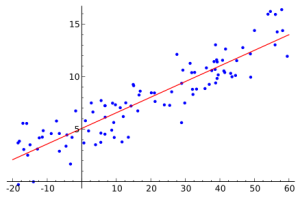
En termes simples, le modèle de régression en statistique mathématique est construit sur la base de données connues, qui sont des paires de nombres. Le nombre de ces paires est prédéterminé. Si vous imaginez que le premier nombre d'une paire est la valeur de la coordonnée $$$x$et le second $$$y$, alors l'ensemble de ces paires de nombres peut être représenté sur le plan dans le système de coordonnées cartésiennes comme un ensemble de points. Ces paires de nombres ne sont pas prises au hasard. En pratique, en règle générale, le deuxième nombre dépend du premier. Construire une régression signifie prendre une ligne (plus précisément une fonction) qui se rapproche le plus possible (se rapproche) d'un grand nombre des points ci-dessus.

À quoi tout cela sert-il? Tout d'abord, cela est nécessaire pour la préparation de la soi-disant prévisions. Besoin souvent de découvrir $$$y$savoir seulement $$$x$s'il diffère de ces X, sur la base desquels la régression a été construite. Je vais donner un exemple simple. Il existe des statistiques sur la dépendance de la croissance d'une personne à son âge sur la base de 100 personnes différentes étudiées. Ainsi, nous avons 100 paires de nombres {âge; croissance}. Dans le même temps, la «croissance» est une quantité dépendante et «l'âge» est indépendant. En construisant correctement un modèle de régression, nous pouvons «prédire» la croissance avec certitude par n'importe quelle valeur d'âge.

En pratique, selon la situation, des fonctions linéaires, paraboliques, de puissance et autres sont utilisées dans la construction de modèles de régression. Dans le cadre des statistiques mathématiques, le modèle de régression linéaire est le plus souvent considéré. Parfois, ils touchent à un cas plus compliqué - un modèle parabolique. En faisant une généralisation, il est facile de deviner que les modèles linéaires et paraboliques sont des cas particuliers d'un modèle plus complexe - polynomial. Construire un modèle de régression signifie trouver les paramètres de la fonction qui y apparaîtra. Pour la régression linéaire - deux paramètres: coefficient et terme libre.

La régression polynomiale peut être utilisée dans les statistiques mathématiques pour modéliser les composantes de tendance des séries chronologiques. Une série chronologique est, en fait, une série de nombres qui dépendent du temps. Par exemple, la température quotidienne moyenne de l'année écoulée ou le revenu mensuel de l'entreprise. L'ordre du polynôme simulé est évalué par des méthodes spéciales, par exemple, par le critère de série. L'objectif de construire un modèle de régression polynomiale dans le domaine des séries chronologiques est toujours le même: la prévision.

Pour commencer, nous considérons le problème de la régression polynomiale de manière générale. Tout raisonnement est basé sur une généralisation du raisonnement dans les problèmes de régression linéaire et parabolique. Après ces considérations, je passerai à un cas spécial - la considération de ce modèle pour les séries chronologiques.

Soit deux séries d'observations données $$$x_i$(variable indépendante) et $$$y_i$(variable dépendante) $$$i = \ overline {1, n}$. L'équation polynomiale a la forme

$$

$$y = \ sum \ limits_ {j = 0} ^ k b_jx ^ j, \ \ \ \ \ (1)$$

où $$$b_j$- paramètres de ce polynôme, $$$j = \ overline {0, k}$. Parmi eux $$$b_0$- un membre gratuit. Trouvons les paramètres des moindres carrés (OLS) $$$b_j$compte tenu de la régression.

Par analogie avec la régression linéaire, OLS est également basé sur la minimisation de l'expression suivante:

$$

$$S = \ sum \ limits_ {i = 1} ^ n \ left (\ hat y_i-y_i \ right) ^ 2 \ to \ min \ \ \ \ \ (2)$$

Ici $$$\ chapeau y_i$- valeurs théoriques qui sont les valeurs du polynôme (1) aux points $$$x_i$. En substituant (1) à (2), on obtient

$$

$$S = \ sum \ limits_ {i = 1} ^ n \ left (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) ^ 2 \ to \ min.$$

Basé sur la condition nécessaire pour l'extrémum de la fonction $$$(k + 1)$les variables $$$S = S (b_0, b_1, \ dots, b_k)$nous assimilons ses dérivées partielles à zéro, c'est-à-dire

$$

$$S '_ {b_p} = 2 \ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (\ sum \ limits_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) = 0, \ \ \ p = \ overline {0, k}.$$

En divisant les côtés gauche et droit de chaque égalité par 2, nous révélons la deuxième somme:

$$

$$\ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (b_0 + b_1x_i + b_2x_i ^ 2 + \ dots + b_kx_i ^ k \ right) - \ sum \ limits_ {i = 1} ^ nx_i ^ py_i = 0 , \ \ \ p = \ overline {0, k}.$$

En ouvrant les crochets, nous transférons dans chacun $$$p$expression, le dernier terme avec $$$y_i$vers la droite et diviser les deux côtés par $$$n$. En conséquence, nous avons $$$(k + 1)$expressions formant un système d'équations normales linéaires pour $$$b_p$. Il a la forme suivante:

$$

$$\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ right. \ \ \ \ \ (3)$$

Vous pouvez réécrire le système (3) sous forme matricielle: $$$AB = C$où

$$

$$A = \ left (\ begin {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ right), \ \ B = \ left (\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right), \ \ C = \ left (\ begin {array} {c} \ overline y \\\ overline {xy} \\ \ overline {x ^ 2y} \\\ vdots \\\ overline {x ^ ky} \ end {array} \ right).$$

Passons maintenant à l'application des faits ci-dessus dans le cas des séries chronologiques. Que les séries chronologiques soient données $$$x_t$où $$$t = \ overline {1, n}$. Il est nécessaire de construire une tendance d'ordre polynomial $$$k$, qui se rapproche le plus précisément possible de la série temporelle donnée. Comme variable indépendante $$$x$nous prendrons $$$t$basé sur la définition d'une série chronologique. Ces X sont une série de nombres naturels qui dénotent une période de temps. En tant que $$$y$les valeurs des séries temporelles sont prises $$$x_t$. On voit que les valeurs des éléments $$$a_ {ij}$matrices système $$$A$indépendant de $$$x_t$. Comme dans le cas général, évidemment,

$$

$$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {i + j-2},$$

puis dans le cas de séries chronologiques

$$

$$a_ {ij} = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {i + j-2},$$

où $$$i, j = \ overline {1, (k + 1)}.$

Articles $$$c_j$vecteurs matriciels de termes libres $$$C$généralement obtenu comme

$$

$$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {j-1} y_r.$$

Et dans le cas des séries chronologiques

$$

$$c_j = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {j-1} x_r,$$

où $$$j = \ overline {1, (k + 1)}.$

Ainsi, après avoir résolu le système (3), nous pouvons trouver les paramètres souhaités de la tendance polynomiale $$$b_0, \ dots, b_k.$

Pour remplir les matrices du système et le résoudre, l'une des méthodes numériques peut être utilisée lors de la modélisation d'une tendance sur un ordinateur. Dans ce cas, le résultat du calcul sera assez précis.

En conséquence, la composante tendance prendra la forme:

$$

$$T_t = \ sum \ limits_ {i = 0} ^ kb_it ^ i, \ \ \ t = 0,1,2, \ dots.$$

Il convient également de noter que la composante de tendance simulée $$$T_t$, déterminé non seulement pour les périodes actuelles $$$[1; n]$, mais aussi pour les périodes futures $$$t> n$.

Je remarque tout de suite que la régression polynomiale ne modélise que la composante tendance de la série chronologique. Un modèle de série chronologique complet implique également d'autres composants, ce qui dépasse le cadre de cet article.

Dans la pratique, je n'ai personnellement pas vu de séries chronologiques avec un ordre de tendance polynomial supérieur à 2. Ceci explique la prévalence des modèles de régression linéaire et prabolique comme cas particuliers de polynôme.