Si vous décrivez en quelques phrases sur quel principe les échanges de tri fonctionnent, alors:

1. Les éléments du tableau sont comparés par paires
2. Si l'élément de gauche ^{* est} plus grand que l'élément de droite, les éléments sont échangés
3. Répétez les étapes 1-2 jusqu'à ce que le tableau soit trié

^{* - l'élément de gauche signifie cet élément de la paire comparée, qui est plus proche du bord gauche du tableau. En conséquence, l'élément de droite est plus proche du bord droit.}

Je m'excuse immédiatement d'avoir répété du matériel bien connu, il est peu probable qu'au moins un des algorithmes de l'article soit une révélation pour vous. A propos de ces tris sur Habré, il a déjà été écrit plusieurs fois (dont moi - 1 , 2 , 3 ) et demande pourquoi revenir sur ce sujet? Mais depuis que j'ai décidé d'écrire une série cohérente d'articles sur tous les tris dans le monde , je dois passer par les méthodes d'échange même dans la version express. Lorsque l'on considère les classes suivantes, il y aura déjà de nombreux nouveaux algorithmes (et peu de gens le savent) qui méritent des articles intéressants distincts.

Traditionnellement, les «échangeurs» incluent des triages dans lesquels les éléments changent (pseudo) aléatoirement (bogosort, bozosort, permsort, etc.). Cependant, je ne les ai pas inclus dans cette classe, car ils manquent de comparaisons. Il y aura un article séparé sur ces triages, où nous philosophons beaucoup sur la théorie des probabilités, la combinatoire et la mort thermique de l'Univers.

Silly Sort :: Sort Stooge

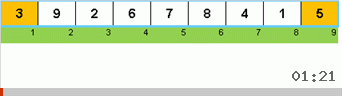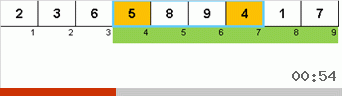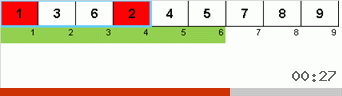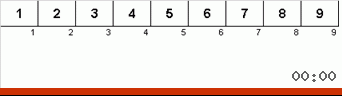
1. Comparez (et modifiez si nécessaire) les éléments aux extrémités du sous-tableau.
2. Nous prenons les deux tiers du sous-tableau depuis son début et appliquons l'algorithme général à ces 2/3 de manière récursive.
3. Nous prenons les deux tiers du sous-tableau de sa fin et appliquons l'algorithme général à ces 2/3 de manière récursive.
4. Et encore une fois, nous prenons les deux tiers du sous-tableau depuis son début et appliquons l'algorithme général à ces 2/3 de manière récursive.

Initialement, un sous-tableau est un tableau entier. Et puis la récursion divise le sous-tableau parent en 2/3, fait des comparaisons / échanges aux extrémités des segments fragmentés, et finalement arrange tout.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

Il a l'air schizophrène, mais il est néanmoins 100% correct.

Tri lent :: Tri lent

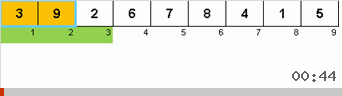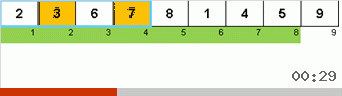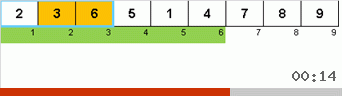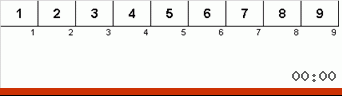
Et ici, nous observons le mysticisme récursif:

1. Si le sous-tableau se compose d'un élément, alors nous terminons la récursivité.
2. Si un sous-tableau se compose de deux éléments ou plus, divisez-le en deux.
3. Nous appliquons l'algorithme récursivement à la moitié gauche.
4. Nous appliquons l'algorithme récursivement à la moitié droite.
5. Les éléments situés aux extrémités du sous-tableau sont comparés (et modifiés si nécessaire).
6. Nous appliquons récursivement l'algorithme à un sous-tableau sans le dernier élément.

Initialement, un sous-tableau est l'ensemble du tableau. Et la récursivité continuera de réduire de moitié, de comparer et de changer jusqu'à ce qu'elle trie tout.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

Cela ressemble à un non-sens, mais le tableau est ordonné.

Pourquoi StoogeSort et SlowSort fonctionnent-ils correctement?

Un lecteur curieux posera une question raisonnable: pourquoi ces deux algorithmes fonctionnent-ils même? Ils semblent simples, mais il n'est pas très évident que vous puissiez trier quelque chose comme ça.

Jetons d'abord un œil au tri lent. Le dernier point de cet algorithme suggère que les efforts récursifs de tri lent ne visent qu'à placer le plus grand élément du sous-tableau dans la position la plus à droite. Ceci est particulièrement visible si vous appliquez l'algorithme à un tableau en ordre inverse:



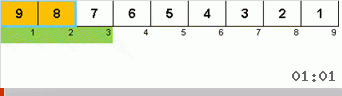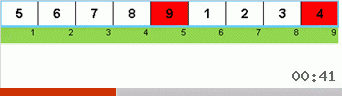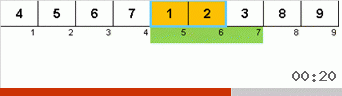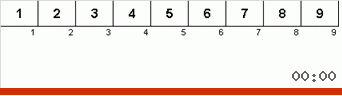
On voit clairement qu'à tous les niveaux de récursivité, les maxima migrent rapidement vers la droite. Ensuite, ces maxima, là où ils sont là où ils sont nécessaires, sont désactivés du jeu: l'algorithme s'appelle lui-même - mais sans le dernier élément.

Dans le genre Stooge, une magie similaire se produit:



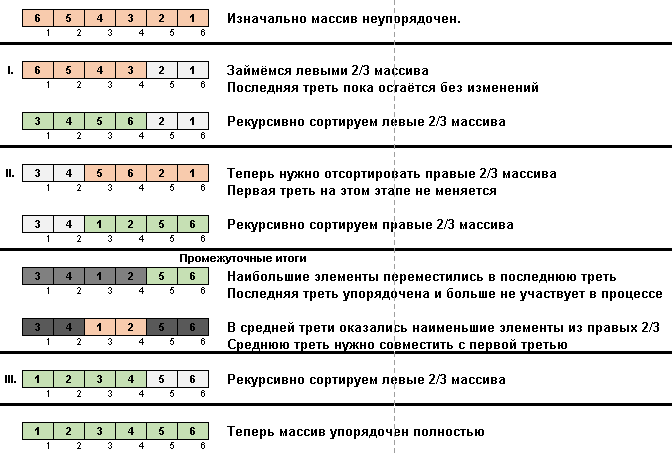
En fait, l'accent est également mis sur le maximum d'éléments. Seul le tri lent les déplace vers la fin un par un, et le tri Stooge pousse un tiers des éléments du sous-tableau (le plus grand d'entre eux) pousse dans le tiers le plus à droite de l'espace cellulaire.

Nous nous tournons vers les algorithmes, où tout est déjà assez évident.

Tri stupide :: Tri stupide

Tri très soigné. Il va du début du tableau à la fin et compare les éléments voisins. Si deux éléments voisins devaient être échangés, alors, juste au cas où, le tri reviendrait au tout début du tableau et recommencerait à nouveau.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

Tri Gnome :: Tri Gnome

Presque la même chose, mais le tri pendant l'échange ne revient pas au tout début du tableau, mais ne fait qu'un pas en arrière. Il s'avère que cela suffit pour tout régler.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

Tri optimisé des nains

Mais vous pouvez économiser non seulement sur la retraite, mais aussi lorsque vous avancez. Avec plusieurs échanges consécutifs, vous devez prendre autant de recul. Et puis il faut revenir en arrière (comparer en cours de route les éléments déjà ordonnés les uns par rapport aux autres). Si vous vous souvenez de la position à partir de laquelle les échanges ont commencé, vous pouvez immédiatement sauter à cette position lorsque les échanges sont terminés.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

Tri des bulles :: Tri des bulles

Contrairement au tri stupide et gnome, lors de l'échange d'éléments dans la bulle, aucun retour ne se produit - il continue d'avancer. Atteignant la fin, le plus grand élément du tableau est déplacé à la toute fin.

Ensuite, le processus de tri répète à nouveau l'ensemble du processus, ce qui fait que le deuxième élément de l'ancienneté se trouve à la dernière mais à une seule place. À l'itération suivante, le troisième élément le plus grand est le troisième à partir de la fin, etc.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

Tri optimisé des bulles

Vous pouvez en profiter un peu dans les allées au début du tableau. Dans le processus, les premiers éléments sont temporairement ordonnés les uns par rapport aux autres (cette partie triée change constamment de taille - elle diminue, elle augmente). Ceci est facilement corrigé et avec une nouvelle itération, vous pouvez simplement sauter par-dessus un groupe de ces éléments.
_{(J'ajouterai ici l'implémentation testée en Python. Je n'ai pas eu le temps de la préparer.)}

Tri Shaker :: Tri Shaker
(Tri cocktail :: Tri cocktail)

Une sorte de bulle. Au premier passage, comme d'habitude - poussez le maximum jusqu'à la fin. Ensuite, nous nous retournons brusquement et poussons le minimum au début. Les zones marginales triées du tableau augmentent en taille après chaque itération.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

Tri pair-impair :: Tri pair-impair

Encore une fois, itérations sur la comparaison par paire d'éléments voisins lors du déplacement de gauche à droite. Tout d'abord, nous comparons les paires dans lesquelles le premier élément est impair en comptage, et le second est pair (c'est-à-dire les premier et deuxième, troisième et quatrième, cinquième et sixième, etc.). Et puis vice versa - pair + impair (deuxième et troisième, quatrième et cinquième, sixième et septième, etc.). Dans ce cas, de nombreux grands éléments du tableau à une même itération font un pas en avant (dans la bulle, le plus grand pour l'itération atteint la fin, mais le reste des assez gros reste presque en place).

Soit dit en passant, il s'agissait à l'origine d'un tri parallèle avec une complexité O (n). Il sera nécessaire d'implémenter AlgoLab dans la section "Tri parallèle".

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

Tri par peigne :: Tri par peigne

La modification la plus réussie de la bulle. L'algorithme de vitesse est en concurrence avec un tri rapide.

Dans toutes les variantes précédentes, nous avons comparé les voisins. Et ici, tout d'abord, on considère des paires d'éléments qui sont à une distance maximale les unes des autres. À chaque nouvelle itération, cette distance se rétrécit uniformément.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

Tri rapide :: Tri rapide

Eh bien, l'algorithme d'échange le plus avancé.

1. Divisez le tableau en deux. L'élément du milieu est la référence.
2. Nous nous déplaçons du bord gauche du tableau vers la droite, jusqu'à ce que nous trouvions un élément plus grand que celui de référence.
3. Nous nous déplaçons du bord droit du tableau vers la gauche jusqu'à ce que nous trouvions un élément plus petit que celui de référence.
4. Nous échangeons les deux éléments trouvés aux points 2 et 3.
5. Nous continuons d'exécuter les points 2-3-4 jusqu'à ce qu'une réunion ait lieu à la suite du mouvement mutuel.
6. Au point de rencontre, le réseau est divisé en deux parties. Pour chaque partie, nous appliquons récursivement un algorithme de tri rapide.

Pourquoi ça marche? À gauche du point de rencontre se trouvent des éléments plus petits ou égaux à celui de référence. À droite du point de rencontre se trouvent des éléments supérieurs ou égaux à la référence. En d'autres termes, tout élément du côté gauche est inférieur ou égal à tout élément du côté droit. Par conséquent, au point de rencontre, le tableau peut être divisé en deux sous-réseaux en toute sécurité et trier chaque sous-réseau de manière similaire de manière récursive.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

Sur Habré, une traduction de l' un des articles est publiée, qui rend compte de la modification de QuickSort, qui surpasse le tri pyramidal de 7 millions d'éléments. Soit dit en passant, c'est en soi une réalisation douteuse, car le tri pyramidal classique ne bat pas les records de performance. En particulier, sa complexité asymptotique n'atteint en aucun cas O (n) (une caractéristique de cet algorithme).

Mais la chose est différente. Selon le pseudo-code de l'auteur (et évidemment incorrect), il n'est généralement pas possible de comprendre quelle est, en fait, l'idée principale de l'algorithme. Personnellement, j'ai eu l'impression que les auteurs sont des escrocs qui ont agi selon cette méthode:

1. Nous déclarons l'invention d'un algorithme de super-tri.
2. Nous renforçons la déclaration avec un pseudo-code non fonctionnel et incompréhensible (comme, intelligent et si clair, mais les imbéciles ne peuvent toujours pas comprendre).
3. Nous présentons des graphiques et des tableaux qui démontreraient la vitesse pratique de l'algorithme sur les mégadonnées. En raison du manque de code réellement fonctionnel, personne ne pourra toujours vérifier ou réfuter ces calculs statistiques.
4. Nous publions des non-sens sur Arxiv.org sous le couvert d'un article scientifique.
5. PROFIT !!!

Peut-être que je parle en vain aux gens et qu'en fait l'algorithme fonctionne? Quelqu'un peut-il expliquer le fonctionnement de k-sort?

UPD Mes accusations massives de tri des auteurs de fraude se sont avérées sans fondement :) L'utilisateur jetsys a compris le pseudo-code de l'algorithme, a écrit une version de travail en PHP et me l'a envoyé dans des messages privés:

Annonce

Ce n'était qu'une théorie, il est temps de passer à la pratique. L'article suivant teste les échanges de tri sur différents ensembles de données. Nous découvrirons:

• Quel tri est le pire - idiot, terne ou terne?
• Les optimisations et les modifications apportées au tri des bulles sont-elles vraiment utiles?
• Dans quelles conditions les algorithmes lents sont-ils facilement rapides en vitesse de QuickSort?

Et lorsque nous trouvons les réponses à ces questions les plus importantes, nous pouvons commencer à étudier la classe suivante - les types d'insertion.

Les références

Application Excel AlgoLab , avec laquelle vous pouvez visualiser étape par étape la visualisation de ces (et pas seulement de ces) sortes.

Wiki / Stupide / Stooge , Lent , Nain / Gnome , Bulle / Bulle , Shaker / Shaker , Impair / Pair , Peigne / Peigne , Rapide / Rapide

Articles de la série

• Application Excel AlgoLab.xlsm
• Exchange Sorts
  • Comparaison de tri Exchange
• Tri d'insertion
• Trier par sélection
• Fusionner les tris
• Trier par distribution
• Tri hybride