Des informations sur l'état de l'environnement ou, par exemple, un certain objet de contrôle peuvent être obtenues en mesurant les valeurs actuelles de paramètres caractérisant certaines propriétés de l'environnement ou de l'objet. Pour recevoir, traiter et transmettre ces informations par des moyens techniques, la valeur du paramètre mesuré doit être convertie par des appareils de mesure automatiques en un signal d'informations de mesure. Pour ce faire, mettre en œuvre le canal de mesure de l'information (
IIC ), en tant que combinaison de moyens techniques, chacun remplissant sa fonction spécifique, à partir de la perception de la valeur mesurée et se terminant par la réception des informations de mesure sous une forme adaptée à la perception humaine ou à son traitement ultérieur. Et tout irait bien, mais le long du chemin des informations, l'interférence
e (t) se superpose au signal utile
y (t) des informations de mesure - une fonction aléatoire du temps qui peut simuler l'erreur aléatoire du transducteur de mesure, des capteurs électriques dans les fils de connexion et des ondulations aléatoires paramètre mesuré et autres facteurs.
Sur cette base, le problème se pose du traitement primaire des informations dans l'IIC - filtrage du signal y (t) des informations de mesure à partir des interférences aléatoires e (t). Fondamentalement, les méthodes de filtrage sont basées sur la différence dans les spectres de fréquence des fonctions y (t) et e (t), et l'interférence est considérée comme plus haute fréquence.
La synthèse du filtre optimal mis en œuvre est une tâche complexe, dont la solution nécessite la spécification exacte des caractéristiques du signal utile et des interférences. Par conséquent, en pratique, la fonction de transfert du filtre est généralement spécifiée et limitée à la synthèse paramétrique à l'aide d'algorithmes de filtrage simples.
Les méthodes de filtration sont effectuées à la fois au niveau logiciel et au niveau matériel. Par exemple, dans le capteur BMP280 (BOSCH), il est possible de connecter un filtre IIR au niveau matériel, en changeant le coefficient de filtre k, si nécessaire, [1].
Filtre IIR
Les filtres à réponse impulsionnelle infinie sont des filtres récursifs et calculent le signal de sortie en fonction des valeurs des échantillons d'entrée et de sortie précédents. Théoriquement, la réponse impulsionnelle d'un filtre IIR n'atteint jamais zéro, la sortie est donc d'une durée infinie.
En général, nous écrivons l'algorithme de filtrage d'un filtre numérique scalaire unidimensionnel comme [2]:
, (1),
où
T est une fonction scalaire d'une variable.
La fonction
T dépend du signal d'entrée actuel x [n], et précédente: M échantillons du signal d'entrée
et N échantillons du signal de sortie
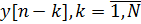
La sortie du filtre IIR est décrite par une équation de différence de la forme:
(2)
où x [n], y [n] est respectivement l'entrée et la sortie du filtre, {
} Est l'ensemble des coefficients directs, M est le nombre de coefficients directs, {
} Est un ensemble de coefficients inverses, N est le nombre de coefficients inverses.
En appliquant la transformation z aux deux côtés de l'équation (2), nous obtenons:
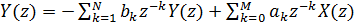
(3).
Ensuite, la fonction de transfert du filtre ressemblera à ceci:
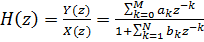
(4)
Algorithme de filtrage d'un filtre IIR unidimensionnel
En termes généraux, l'algorithme de filtrage pour un filtre récursif stationnaire scalaire unidimensionnel ressemble à ceci:
. (5)
Nous écrivons maintenant l'équation de différence pour le filtre IIR sous la forme [1]:
(6)
où k est le coefficient de filtrage;
ou
(7)
où
Sont les coefficients de filtre inverse et direct, respectivement.
D'après (7), il est évident qu'à k = 1, le signal de sortie du filtre répétera l'entrée, et à mesure que le coefficient de filtre k augmente, le poids du signal filtré précédent tend vers 1 et le poids de la valeur mesurée tend vers 0.
L'algorithme (6) est implémenté comme exemple du canal de mesure des informations de pression atmosphérique absolue pour le capteur BMP280, au niveau logiciel dans l'environnement de développement Arduino Software (IDE), liste 1. Le schéma de connexion électrique des composants IIC est illustré à la Fig. 1. La vue générale du prototype IIC de pression atmosphérique absolue est présentée à la Fig. 2. Le prototype offre la possibilité de modifier le coefficient de filtrage dans la plage de 1 ... 50 par incréments de 1, en tournant le bouton du potentiomètre. Le signe de l'affichage à cristaux liquides indique la valeur de pression mesurée (pour k = 1) ou la valeur filtrée (pour k = 2 ... 50), et le coefficient de filtre k.
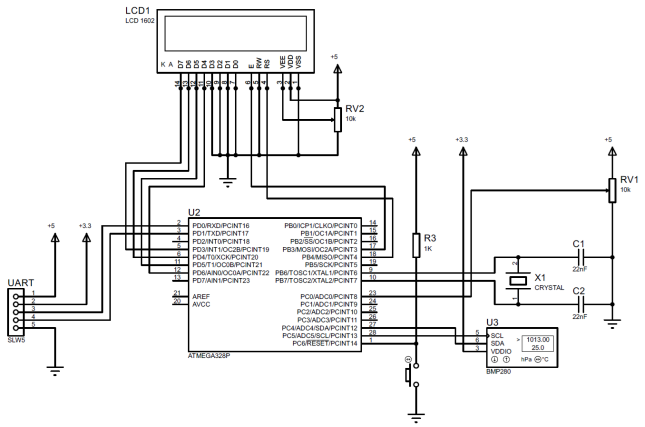Fig. 1 - Schéma de câblage des composants du prototype IIC
Fig. 2 - Vue générale du prototype IICScript Python pour la recherche de filtres IIR
Le listing 2 montre un script Python pour examiner les filtres IIR. Le coefficient de filtre k est écrit dans le script. Les valeurs de pression mesurées sont lues séquentiellement à partir du port COM virtuel et filtrées. Les valeurs mesurées et filtrées du paramètre mesuré en temps réel sont affichées dans la fenêtre graphique et sur la console. Les résultats de l'expérience sont enregistrés par le tableau dans un fichier et les chronologies des valeurs mesurées et filtrées sont affichées dans la fenêtre graphique.
Listing 2 import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import datetime, time k = 6.0
Résultats de l'expérience
: 33 : 6 : COM6 : n - ; P - , ; n P 0 100490.00 100490.00 1 100488.00 100489.71 2 100487.00 100489.33 3 100488.00 100489.14 4 100488.00 100488.97 … 30 100486.00 100488.14 31 100492.00 100488.70 32 100489.00 100488.74 : 16.028, c : 0.500875, c 275_count.txt Ctrl-C,
Conclusions
L'algorithme de filtrage ci-dessus est très simple dans l'implémentation logicielle et, dans la pratique, peut être utilisé dans des IIC similaires à ceux abordés dans cet article.
Losikhin D.A., s.v. café CITYM .
Sources d'information
- Capteur de pression numérique BMP280
- Filtre de réponse impulsionnelle infinie