Dans cette série d'articles, vous vous familiariserez avec les principes de base de la programmation fonctionnelle et comprendrez ce que signifie «penser fonctionnellement» et en quoi cette approche diffère de la programmation orientée objet ou impérative.

Maintenant que vous avez vu certaines des raisons pour lesquelles vous devriez utiliser F #, dans l'article « Plonger en F #. Un guide pour les développeurs C # », prenez du recul et discutez des bases de la programmation fonctionnelle. Que signifie réellement la «programmation fonctionnelle» et en quoi cette approche diffère-t-elle de la programmation orientée objet ou impérative?
Changement de mentalité (Intro)
Il est important de comprendre que la programmation fonctionnelle n'est pas seulement un style de programmation distinct. Il s'agit d'une façon complètement différente de penser en programmation, qui diffère de l'approche «traditionnelle» aussi sensiblement que la POO actuelle (dans le style Smalltalk) diffère d'un langage impératif traditionnel tel que C.
F # vous permet d'utiliser des styles de codage non fonctionnels, ce qui incite le programmeur à conserver ses habitudes existantes. Vous pouvez programmer en F # comme vous en avez l'habitude, sans changer radicalement la vision du monde, et sans même savoir ce que vous manquez. Cependant, afin de tirer le meilleur parti de F #, et aussi d'apprendre à programmer en toute confiance dans un style fonctionnel en général, il est très important d'apprendre à penser de manière fonctionnelle et non impérative.
Le but de cette série d'articles est d'aider le lecteur à comprendre le contexte de la programmation fonctionnelle et à changer sa façon de penser.
Ce sera une série assez abstraite, bien que j'utiliserai de nombreux exemples de code courts pour illustrer certains points. Nous couvrirons les sujets suivants:
- Fonctions mathématiques . Le premier article présente les concepts mathématiques qui sous-tendent les langages fonctionnels et les avantages que cette approche apporte.
- Fonctions et valeurs . Ce qui suit présente les fonctions et les valeurs, explique en quoi les «valeurs» diffèrent des variables et quelles sont les similitudes entre les fonctions et les valeurs simples.
- Types . Ensuite, nous passons aux principaux types qui fonctionnent avec les fonctions: les types primitifs tels que string et int, le type d'unité, les types fonctionnels et les types génériques.
- Fonctions avec plusieurs paramètres . J'expliquerai plus en détail les concepts de «curry» et «d'application partielle». À cet endroit, le cerveau de quelqu'un sera blessé, surtout si ces cerveaux n'ont qu'un passé impératif.
- Définition des fonctions . Ensuite, plusieurs articles seront consacrés à de nombreuses façons différentes de définir et de combiner les fonctions.
- Signatures de fonctions . Ce qui suit est un article important sur la valeur critique des signatures de fonction, ce qu'elles signifient et comment utiliser les signatures pour comprendre le contenu des fonctions.
- Organisation des fonctions . Quand il devient clair comment créer des fonctions, la question se pose: comment pouvez-vous les organiser pour les rendre accessibles au reste du code?
Fonctions mathématiques
La programmation fonctionnelle est inspirée des mathématiques. Les fonctions mathématiques ont un certain nombre de fonctionnalités très intéressantes que les langages fonctionnels tentent d'implémenter.
Commençons par une fonction mathématique qui ajoute 1 à un nombre.
Add1(x) = x+1
Que signifie vraiment cette expression? Cela semble assez simple. Cela signifie qu'il existe une telle opération qui prend un nombre et y ajoute 1.
Ajoutez de la terminologie:
- L'ensemble des valeurs de fonction d'entrée valides est appelé domaine (portée). Dans cet exemple, il pourrait s'agir de nombres réels, mais nous simplifierons la vie et nous limiterons ici à des nombres entiers.
- L'ensemble des résultats possibles de la fonction (plage de valeurs) est appelé plage (techniquement, l'image du codomaine ). Dans ce cas, il existe également de nombreux entiers.
- Une fonction est appelée un mappage (dans la carte d' origine) du domaine à la plage. (C'est-à-dire de la portée à la portée.)
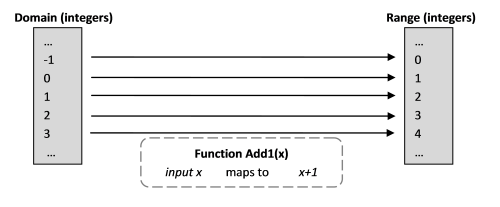
Voici à quoi ressemblera cette définition en F #.
let add1 x = x + 1
Si vous le saisissez dans F # Interactive (n'oubliez pas les doubles points-virgules), alors vous pouvez voir le résultat (la "signature" de la fonction):
val add1 : int -> int
Considérez la conclusion en détail:
- La signification générale est que la fonction
add1 compare des entiers (du domaine de définition) avec des entiers (de la plage de valeurs). - "
add1 " est défini comme "val", abréviation de "valeur". Hm? qu'est-ce que cela signifie Nous en discuterons un peu plus tard. - La notation de flèche «->» est utilisée pour montrer le domaine et la plage. Dans ce cas, le domaine est de type «int», comme range.
Notez que le type n'a pas été explicitement spécifié, mais le compilateur F # a décidé que la fonction fonctionne avec des entiers. (Cela peut-il être changé? Oui, et bientôt nous le verrons).
Propriétés clés des fonctions mathématiques
Les fonctions mathématiques ont un certain nombre de propriétés qui les distinguent beaucoup des fonctions utilisées dans la programmation procédurale.
- Une fonction a toujours le même résultat pour la même valeur d'entrée.
- La fonction n'a aucun effet secondaire.
Ces propriétés offrent un certain nombre d'avantages notables que les langages de programmation fonctionnels tentent de réaliser autant que possible dans leur conception. Nous les examinerons tour à tour.
Les fonctions mathématiques retournent toujours le même résultat à une valeur donnée
Dans la programmation impérative, nous pensons que les fonctions «font» quelque chose ou «comptent» quelque chose. Les fonctions mathématiques ne comptent rien, ce sont des mappages purs de l'entrée à la sortie. En fait, une autre définition d'une fonction est un simple ensemble de tous les mappages. Par exemple, il est très grossièrement possible de définir la fonction «add1» (en C #) comme
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
Évidemment, il est impossible d'avoir un étui pour chaque nombre possible, mais le principe est le même. Avec ce paramètre, aucun calcul n'est effectué, seule une recherche est effectuée.
Fonctions mathématiques sans effets secondaires
Dans une fonction mathématique, les valeurs d'entrée et de sortie sont logiquement deux choses différentes, toutes deux étant prédéfinies. La fonction ne modifie pas les données d'entrée ou de sortie et mappe simplement la valeur d'entrée prédéfinie de la zone de définition à la valeur de sortie prédéfinie dans la zone de valeur.
En d'autres termes, un calcul de fonction ne peut avoir aucun effet sur les données d'entrée ou quoi que ce soit d'autre du genre . Il faut se rappeler que le calcul d'une fonction ne compte ni ne manipule vraiment rien, c'est juste une recherche surfaite.
Cette «immuabilité» des valeurs est très subtile, mais en même temps très importante. Quand je fais des calculs, je ne m'attends pas à ce que les nombres changent au fur et à mesure qu'ils sont ajoutés. Par exemple, si j'ai:
x = 5 y = x+1
Je ne m'attends pas à ce que x change lorsque j'ajoute 1. Je m'attends à obtenir un nombre différent ( y ), et x ne doit pas être modifié. Dans le monde des mathématiques, les entiers existent déjà dans un ensemble immuable et la fonction add1 détermine simplement la relation entre eux.
Le pouvoir de la fonction pure
Ces types de fonctions qui ont des résultats reproductibles et n'ont pas d'effets secondaires sont appelées «fonctions pures», et vous pouvez faire des choses intéressantes avec elles:
- Ils sont faciles à paralléliser. Disons, nous pourrions prendre des entiers dans la plage de 1 à 1000 et les distribuer à 1000 processeurs différents, après quoi nous demandons à chaque CPU d'exécuter «
add1 » sur le nombre correspondant, tout en étant sûr qu'il n'y a pas besoin d'interaction entre eux. Pas de verrous, pas de mutex, pas de sémaphores, etc. - Vous pouvez utiliser les fonctions paresseusement, en les calculant si nécessaire pour la logique du programme. Vous pouvez être sûr que la réponse sera exactement la même, que les calculs soient effectués maintenant ou plus tard.
- Vous pouvez uniquement effectuer des calculs de fonction pour une entrée spécifique, puis mettre en cache le résultat, car il est connu que ces valeurs d'entrée donneront la même sortie.
- S'il existe de nombreuses fonctions pures, elles peuvent être calculées dans n'importe quel ordre. Encore une fois, cela ne peut pas affecter le résultat final.
Par conséquent, s'il est possible de créer des fonctions pures dans un langage de programmation, vous pouvez immédiatement recevoir de nombreuses astuces puissantes. Et sans aucun doute, tout cela peut être fait en F #:
- Un exemple de calcul parallèle était dans la série "Pourquoi utiliser F #?" .
- Le calcul des fonctions paresseuses sera discuté dans la série Optimisation .
- La mise en cache des résultats de la fonction est appelée mémorisation et sera également discutée dans la série Optimisation .
- L'absence de la nécessité de suivre l'ordre d'exécution rend la programmation parallèle beaucoup plus facile et élimine le besoin de bogues causés par la modification de l'ordre des fonctions ou la refactorisation.
Propriétés "inutiles" des fonctions mathématiques
Les fonctions mathématiques ont également des propriétés qui ne semblent pas très utiles lors de la programmation.
- Les valeurs d'entrée et de sortie sont immuables
- Les fonctions ont toujours une entrée et une sortie.
Ces propriétés se reflètent dans la conception des langages de programmation fonctionnels. Il convient de les considérer séparément.
Les valeurs d'entrée et de sortie sont immuables
Les valeurs immuables en théorie semblent être une bonne idée, mais comment peut-on vraiment faire un travail s'il n'y a aucun moyen d'affecter une variable de la manière traditionnelle.
Je peux vous assurer que ce n'est pas un gros problème comme vous pouvez l'imaginer. Dans cette série d'articles, il sera clair comment cela fonctionne dans la pratique.
Les fonctions mathématiques ont toujours une entrée et une sortie.
Comme le montrent les diagrammes, pour une fonction mathématique, il n'y a toujours qu'une seule entrée et une seule sortie. Cela est également vrai pour les langages de programmation fonctionnels, même si cela peut ne pas être évident lors de la première utilisation.
Cela semble être un gros inconvénient. Comment puis-je faire quelque chose d'utile sans fonctions avec deux (ou plus) paramètres?
Il s'avère qu'il existe un moyen de le faire, et de plus, il est complètement transparent sur F #. Il est appelé "curry" et mérite un poste séparé, qui apparaîtra dans un proche avenir.
En fait, il deviendra plus tard clair que ces deux propriétés «inutiles» deviendront incroyablement précieuses et seront l'élément clé qui rend la programmation fonctionnelle si puissante.
Ressources supplémentaires
Il existe de nombreux didacticiels pour F #, y compris des documents pour ceux qui viennent avec une expérience C # ou Java. Les liens suivants peuvent être utiles pour approfondir F #:
Plusieurs autres façons de commencer à apprendre le F # sont également décrites.
Enfin, la communauté F # est très conviviale pour les débutants. Il y a un chat très actif chez Slack, soutenu par la F # Software Foundation, avec des salles pour débutants que vous pouvez rejoindre librement . Nous vous recommandons fortement de le faire!
N'oubliez pas de visiter le site de la communauté russophone F # ! Si vous avez des questions sur l'apprentissage d'une langue, nous serons heureux d'en discuter dans les salles de chat:
À propos des auteurs de traduction
Traduit par @kleidemos
 La traduction et les modifications éditoriales ont été apportées par les efforts de la communauté russophone des développeurs F # . Nous remercions également @schvepsss et @shwars d' avoir préparé cet article pour publication.
La traduction et les modifications éditoriales ont été apportées par les efforts de la communauté russophone des développeurs F # . Nous remercions également @schvepsss et @shwars d' avoir préparé cet article pour publication.