Cartographie normale

Toutes les scènes que nous utilisons sont constituées de polygones, eux-mêmes constitués de centaines, de milliers de triangles absolument plats. Nous avons déjà réussi à augmenter légèrement le réalisme des scènes grâce à des détails supplémentaires qui fournissent l'application de textures bidimensionnelles sur ces triangles plats. La texturation permet de masquer le fait que tous les objets de la scène ne sont qu'une collection de nombreux petits triangles. Une grande technique, mais ses possibilités ne sont pas illimitées: à l'approche de n'importe quelle surface, tout le monde se rend compte qu'elle est constituée de surfaces planes. La plupart des objets réels ne sont pas complètement plats et montrent beaucoup de détails en relief.


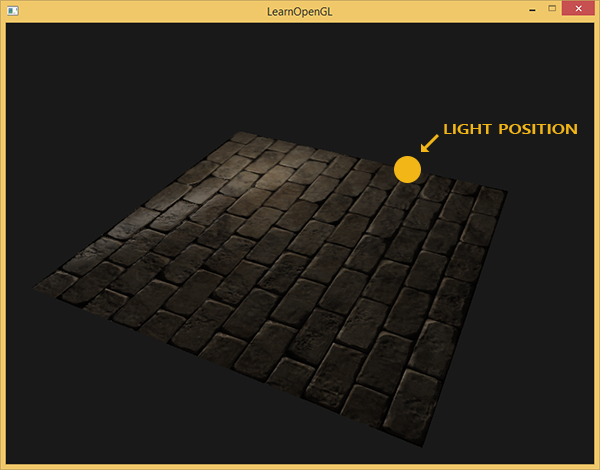
Par exemple, prenez la maçonnerie. Sa surface est très rugueuse et, évidemment, n'est pas représentée par un plan: il y a des évidements avec du ciment et de nombreux petits détails tels que des trous et des fissures. Si nous analysons une scène avec imitation de maçonnerie en présence d'éclairage, l'illusion d'un relief de surface est très facilement détruite. Voici un exemple d'une telle scène contenant un plan avec une texture de maçonnerie et une source de lumière ponctuelle:


Comme vous pouvez le voir, l'éclairage ne prend pas du tout en compte les détails de relief supposés pour cette surface: toutes les petites fissures et cavités avec du ciment sont également indiscernables du reste de la surface. On pourrait utiliser une carte brillante spéculaire afin de limiter l'illumination de certains détails qui se trouvent dans les creux de la surface. Mais cela ressemble plus à un hack sale qu'à une solution de travail. Ce dont nous avons besoin, c'est d'un moyen de fournir aux équations d'éclairage des données sur le microrelief en surface.
Dans le cadre des équations d'éclairage connues de nous, considérons cette question: dans quelles conditions la surface sera-t-elle illuminée comme parfaitement plane? La réponse est liée à la normale à la surface. Du point de vue de l'algorithme d'éclairage, les informations sur la forme de la surface ne sont transmises que par le vecteur normal. Puisque le vecteur normal est constant partout sur la surface présentée ci-dessus, l'illumination sort également uniforme, correspondant au plan. Mais que se passe-t-il si nous passons à l'algorithme d'éclairage non pas la seule constante normale pour tous les fragments appartenant à l'objet, mais la normale unique pour chaque fragment? Ainsi, le vecteur normal changera légèrement en fonction de la topographie de la surface, ce qui créera une illusion plus convaincante de la complexité de la surface:


Grâce à l'utilisation de normales fragmentairement différentes, l'algorithme d'éclairage considérera la surface comme composée de nombreux plans microscopiques perpendiculaires à son vecteur normal. En conséquence, cela ajoutera considérablement de la texture à l'objet. La technique d'application de normales uniques à un fragment, et non à toute la surface - c'est la cartographie normale ou la cartographie de relief . Comme appliqué à une scène déjà familière:


Vous pouvez voir l'augmentation impressionnante de la complexité visuelle en raison du coût très modeste des performances. Puisque nous sommes tous des changements dans le modèle d'éclairage qui ne sont que dans la fourniture d'une normale unique dans chaque fragment, aucune formule de calcul n'est modifiée. Ce n'est qu'à l'entrée, au lieu de la normale interpolée, que la normale du fragment courant vient à la surface. Toutes les mêmes équations d'éclairage font le reste du travail pour créer l'illusion de relief.

Cartographie normale

Il s'avère donc que nous devons fournir à l'algorithme d'éclairage des normales qui sont uniques à chaque fragment. Nous utiliserons la méthode déjà familière dans les textures de réflexion diffuse et spéculaire et utiliserons la texture 2D habituelle pour stocker des données normales à chaque point de la surface. Ne soyez pas surpris, les textures sont également idéales pour stocker des vecteurs normaux. Il suffit ensuite de sélectionner dans la texture, de restaurer le vecteur normal et d'effectuer des calculs d'éclairage.

À première vue, il peut ne pas être très clair comment enregistrer les données vectorielles dans une texture régulière, qui est généralement utilisée pour stocker des informations sur les couleurs. Mais réfléchissez un instant: la triade de couleurs RVB est essentiellement un vecteur tridimensionnel. De la même manière, vous pouvez enregistrer les composants du vecteur normal XYZ dans les composants de couleur correspondants. Les valeurs des composantes du vecteur normal se situent dans l'intervalle [-1, 1] et nécessitent donc une conversion supplémentaire à l'intervalle [0, 1]:

vec3 rgb_normal = normal * 0.5 + 0.5; //   [-1,1]  [0,1] 

Une telle réduction du vecteur normal à l'espace des composantes de couleur RVB nous permettra de sauvegarder le vecteur normal dans la texture, obtenu sur la base du relief réel de l'objet modélisé et unique pour chaque fragment. Un exemple d'une telle texture - cartes normales - pour la même maçonnerie:


Il est intéressant de noter la teinte bleue de cette carte normale (presque toutes les cartes normales ont une teinte similaire). Cela se produit parce que toutes les normales sont orientées approximativement le long de l'axe oZ, qui est représenté par le triple de coordonnées (0, 0, 1), c'est-à-dire sous la forme d'une triade de couleurs - bleu pur. De petits changements de teinte sont la conséquence de la déviation des normales du demi-axe positif oZ dans certaines zones, ce qui correspond à un terrain inégal. Ainsi, vous pouvez voir que sur les bords supérieurs de chaque brique, la texture prend une teinte verte. Et c'est logique: sur les faces supérieures de la brique, les normales doivent être davantage orientées vers l'axe oY (0, 1, 0), ce qui correspond au vert.

Pour la scène de test, prenez un plan orienté vers le demi-axe positif oZ et utilisez pour cela la carte diffuse et la carte normale suivantes .

Veuillez noter que la carte normale sur le lien et dans l'image ci-dessus est différente. Dans l'article, l'auteur mentionne plutôt nonchalamment les raisons des différences, se limitant à conseiller les cartes normales à convertir de sorte que la composante verte indique «bas» plutôt que «haut» dans le système local au plan de texture.
Si vous regardez plus en détail, deux facteurs interagissent ici:

• La différence réside dans la façon dont les texels sont traités dans la mémoire client et dans la mémoire de texture OpenGL
• La présence de deux notations pour les cartes normales. Classiquement, deux camps: style DirectX et style OpenGL

En ce qui concerne les notations normales de carte, deux camps sont historiquement familiers: DirectX et OpenGL.

Apparemment, ils ne sont pas compatibles. Et avec un peu de réflexion, vous pouvez comprendre que DirectX considère l'espace tangent comme étant gaucher et OpenGL comme droitier. Faire glisser la carte normale X de notre application sans aucune modification entraînera un éclairage incorrect, et il n'est pas toujours immédiatement clair qu'elle est incorrecte. Plus particulièrement, les renflements au format OpenGL deviennent des indentations pour DirectX et vice versa.
Quant à l'adressage: chargement des données d'un fichier de texture en mémoire, nous supposons que le premier texel est le texel supérieur gauche de l'image. Pour représenter des données de texture dans la mémoire d'application, cela est généralement vrai. Mais OpenGL utilise un système de coordonnées de texture différent: pour cela, le premier texel est en bas à gauche. Pour une texturation correcte, les images sont généralement inversées le long de l'axe Y dans le code de l'un ou l'autre chargeur de fichier image. Pour Stb_image utilisé dans les leçons, vous devez ajouter une case à cocher

 stbi_set_flip_vertically_on_load(1); 

Le plus drôle est que deux options sont correctement affichées en termes d'éclairage: une carte normale en notation OpenGL avec réflexion Y activée ou une carte normale en notation DirectX avec réflexion Y désactivée. L'éclairage dans les deux cas fonctionne correctement, la différence ne restera que dans l'inverse de la texture le long de l'axe Y.

Remarque trans.

Donc, chargez les deux textures, liez-les aux blocs de texture et rendez le plan préparé, en tenant compte des modifications suivantes du code du shader de fragment:

 uniform sampler2D normalMap; void main() { //         [0,1] normal = texture(normalMap, fs_in.TexCoords).rgb; //      [-1,1] normal = normalize(normal * 2.0 - 1.0); [...] //  ... } 

Ici, nous appliquons la transformation inverse de l'espace de valeurs RVB à un vecteur normal complet, puis nous l'utilisons simplement dans le modèle d'éclairage Blinn-Fong bien connu.

Maintenant, si vous changez lentement la position de la source de lumière dans la scène, vous pouvez sentir l'illusion du relief de surface fourni par la carte normale:


Mais il reste un problème qui réduit considérablement la plage d'utilisation possible des cartes normales. Comme déjà noté, la teinte bleue de la carte normale laissait entendre que tous les vecteurs de la texture sont orientés en moyenne le long de l'axe positif oZ. Dans notre scène, cela n'a pas créé de problèmes, car la normale à la surface de l'avion était également alignée avec oZ. Cependant, que se passe-t-il si nous modifions la position du plan dans la scène afin que la normale à celui-ci soit alignée avec l'axe positif oY?


L'éclairage s'est avéré complètement faux! Et la raison est simple: les normales de la carte renvoient toujours des vecteurs orientés le long du demi-axe positif oZ, bien que dans ce cas, ils devraient être orientés dans la direction du demi-axe positif oY de la normale de surface. Dans le même temps, le calcul de l'éclairage est comme si les normales à la surface étaient situées comme si le plan était toujours orienté vers le demi-axe positif oZ, ce qui donne un résultat incorrect. La figure ci-dessous montre plus clairement l'orientation des normales lues sur la carte par rapport à la surface:


On peut voir que les normales sont généralement alignées le long du demi-axe positif oZ, bien qu'elles auraient dû être alignées le long de la normale à la surface qui est dirigée le long du demi-axe positif oY.
Une solution possible serait d'établir une carte normale distincte pour chaque orientation de la surface considérée. Pour un cube, six cartes normales seraient nécessaires, mais pour des modèles plus complexes, le nombre d'orientations possibles peut être trop élevé et ne pas convenir à la mise en œuvre.

Il existe une autre approche, mathématiquement plus compliquée, qui propose de calculer l'éclairage dans un système de coordonnées différent: de telle sorte que les vecteurs normaux coïncident toujours approximativement avec le demi-axe positif oZ. Les autres vecteurs requis pour les calculs d'éclairage sont ensuite convertis dans ce système de coordonnées. Cette méthode permet d'utiliser une carte normale pour n'importe quelle orientation de l'objet. Et ce système de coordonnées spécifique est appelé espace tangent ou espace tangent .

Espace tangent

Il convient de noter que le vecteur normal dans la carte normale est exprimé directement dans l'espace tangent, c'est-à-dire dans un système de coordonnées tel que la normale soit toujours dirigée approximativement dans la direction du demi-axe positif oZ. L'espace tangent est défini comme un système de coordonnées local au plan du triangle, et chaque vecteur normal est défini dans ce système de coordonnées. Vous pouvez imaginer ce système comme un système de coordonnées locales pour une carte normale: tous les vecteurs qu'il contient sont dirigés vers le demi-axe positif oZ, quelle que soit l'orientation finale de la surface. En utilisant des matrices de transformation spécialement préparées, il est possible de transformer des vecteurs normaux de ce système de coordonnées tangentes locales en coordonnées mondiales ou de vue, en les orientant en fonction de la position finale des surfaces texturées.
Prenons l'exemple précédent avec l'utilisation incorrecte de la cartographie normale, où le plan était orienté le long de l'axe positif oY. Étant donné que la carte des normales est définie dans l'espace tangent, l'une des options de réglage consiste à calculer la matrice de transition des normales de l'espace tangent à celles-ci devenant orientées normalement par rapport à la surface. Cela entraînerait l'alignement des normales le long de l'axe positif oY. Une propriété remarquable de l'espace tangent est le fait qu'en calculant une telle matrice nous pouvons réorienter les normales vers n'importe quelle surface et son orientation.

Une telle matrice est abrégée en TBN , qui est une abréviation pour le nom du triple des vecteurs Tangent , Bitangent et Normal . Nous devons trouver ces trois vecteurs afin de former cette matrice de changement de base. Une telle matrice fait la transition d'un vecteur de l'espace tangent à un autre et pour sa formation trois vecteurs mutuellement perpendiculaires sont nécessaires, dont l'orientation correspond à l'orientation du plan normal de la carte. C'est un vecteur de direction vers le haut, vers la droite et vers l'avant, un ensemble qui nous est familier de la leçon sur la caméra virtuelle .
Avec le vecteur du haut, tout est clair tout de suite - c'est notre vecteur normal. Les vecteurs droit et avant sont respectivement appelés tangents et bitangents . La figure suivante donne une idée de leur position relative sur le plan:


Le calcul de la tangente et de la bi-tangente n'est pas aussi évident que le calcul du vecteur normal. Dans la figure, vous pouvez voir que les directions de la tangente et la carte tangente de la normale sont alignées avec les axes qui spécifient les coordonnées de texture de la surface. Ce fait est la base du calcul de ces deux vecteurs, ce qui nécessitera une certaine compétence en mathématiques. Regardez l'image:


Modifications des coordonnées de texture le long d'une face triangulaire $$$E_2$désigné comme $$$\ Delta U_2$et $$$\ Delta V_2$exprimé dans les mêmes directions que les vecteurs tangents $$$T$et bi-tangente $$$B$. Sur la base de ce fait, vous pouvez exprimer les bords d'un triangle $$$E_1$et $$$E_2$sous la forme d'une combinaison linéaire de vecteurs tangents et bi-tangents:

$$

$$E_1 = \ Delta U_1T + \ Delta V_1B$$

$$

$$E_2 = \ Delta U_2T + \ Delta V_2B$$

En nous transformant en un enregistrement au niveau du bit, nous obtenons:

$$

$$(E_ {1x}, E_ {1y}, E_ {1z}) = \ Delta U_1 (T_x, T_y, T_z) + \ Delta V_1 (B_x, B_y, B_z)$$

$$

$$(E_ {2x}, E_ {2y}, E_ {2z}) = \ Delta U_2 (T_x, T_y, T_z) + \ Delta V_2 (B_x, B_y, B_z)$$

$$$E$est calculé comme le vecteur de la différence de deux vecteurs, et $$$\ Delta U$et $$$\ Delta V$comme la différence de coordonnées de texture. Reste à trouver deux inconnues dans deux équations: la tangente $$$T$et biais $$$B$. Si vous vous souvenez des leçons d'algèbre, vous savez que de telles conditions permettent de résoudre le système de $$$T$et pour $$$B$.
La dernière forme d'équations donnée nous permet de la réécrire sous forme de multiplication matricielle:

$$

$$\ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Essayez de faire une multiplication matricielle dans votre esprit pour vous assurer que l'enregistrement est correct. L'écriture d'un système sous forme matricielle facilite la compréhension de l'approche de recherche $$$T$et $$$B$. Multipliez les deux côtés de l'équation par l'inverse de $$$\ Delta U \ Delta V$:

$$

$$\ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} ^ {- 1} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z } \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Nous obtenons une décision concernant $$$T$et $$$B$, ce qui nécessite cependant le calcul de la matrice inverse des changements de coordonnées de texture. Nous n'entrerons pas dans les détails du calcul des matrices inverses - l'expression de la matrice inverse ressemble au produit du nombre inverse du déterminant de la matrice d'origine et de la matrice adjointe:

$$

$$\ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix} = \ frac {1} {\ Delta U_1 \ Delta V_2 - \ Delta U_2 \ Delta V_1} \ begin {bmatrix} \ Delta V_2 & - \ Delta V_1 \\ - \ Delta U_2 & \ Delta U_1 \ end {bmatrix} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ { 2y} & E_ {2z} \ end {bmatrix}$$

Cette expression est la formule de calcul du vecteur tangent $$$T$et bi-tangente $$$B$basé sur les coordonnées des faces du triangle et les coordonnées de texture correspondantes.
Ne vous inquiétez pas si l'essence des calculs mathématiques ci-dessus vous échappe. Si vous comprenez que nous obtenons la tangente et la tangente de biais en fonction des coordonnées des sommets du triangle et de leurs coordonnées de texture (puisque les coordonnées de texture appartiennent également à l'espace tangent) - c'est déjà la moitié de la bataille.

Calcul des tangentes et des bitangentes

Dans l'exemple de cette leçon, nous avons pris un plan simple en regardant vers le demi-axe positif oZ. Nous allons maintenant essayer d'implémenter une cartographie normale en utilisant l'espace tangent afin de pouvoir orienter le plan dans l'exemple comme nous le souhaitons sans détruire l'effet de cartographie normal. En utilisant le calcul ci-dessus, nous trouvons manuellement la tangente et la bi-tangente à la surface considérée.
Nous supposons que le plan est composé des sommets suivants avec des coordonnées de texture (deux triangles sont donnés par les vecteurs 1, 2, 3 et 1, 3, 4):

 //   glm::vec3 pos1(-1.0, 1.0, 0.0); glm::vec3 pos2(-1.0, -1.0, 0.0); glm::vec3 pos3( 1.0, -1.0, 0.0); glm::vec3 pos4( 1.0, 1.0, 0.0); //   glm::vec2 uv1(0.0, 1.0); glm::vec2 uv2(0.0, 0.0); glm::vec2 uv3(1.0, 0.0); glm::vec2 uv4(1.0, 1.0); //   glm::vec3 nm(0.0, 0.0, 1.0); 

Dans un premier temps, nous calculons les vecteurs décrivant les faces du triangle, ainsi que les deltas des coordonnées de texture:

 glm::vec3 edge1 = pos2 - pos1; glm::vec3 edge2 = pos3 - pos1; glm::vec2 deltaUV1 = uv2 - uv1; glm::vec2 deltaUV2 = uv3 - uv1; 

Ayant en main les données initiales nécessaires, nous pouvons commencer à calculer la tangente et la bi-tangente directement par les formules de la section précédente:

 float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y); tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x); tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y); tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z); tangent1 = glm::normalize(tangent1); bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x); bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y); bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z); bitangent1 = glm::normalize(bitangent1); [...] //         

Tout d'abord, nous retirons la composante fractionnaire de l'expression finale dans une variable distincte f . Ensuite, pour chaque composante des vecteurs, nous effectuons la partie correspondante de la multiplication matricielle et multiplions par f . En comparant ce code avec la formule de calcul finale, vous pouvez voir que c'est son arrangement littéral. N'oubliez pas de normaliser à la fin, afin que les vecteurs trouvés soient unitaires.

Puisque le triangle est une figure plate, il suffit de calculer la tangente et la bi-tangente une fois par triangle - elles seront les mêmes pour tous les sommets. Il convient de noter que la plupart des implémentations de travail avec des modèles (tels que des chargeurs ou des générateurs de paysage) utilisent une telle organisation de triangles, où ils partagent des sommets avec d'autres triangles. Dans de tels cas, les développeurs ont généralement recours à des paramètres de moyenne aux sommets communs, tels que les vecteurs normaux, tangents et bi-tangents, pour obtenir un résultat plus fluide. Les triangles qui composent notre plan partagent également plusieurs sommets, mais comme ils se trouvent tous deux dans le même plan, la moyenne n'est pas requise. Néanmoins, il est utile de rappeler la présence d'une telle approche dans des applications et tâches réelles.

Les vecteurs tangents et bi-tangents résultants doivent avoir des valeurs (1, 0, 0) et (0, 1, 0), respectivement. Cela avec le vecteur normal (0, 0, 1) forme la matrice orthogonale TBN. Si vous visualisez la base résultante avec l'avion, vous obtenez l'image suivante:


Maintenant, après avoir calculé les vecteurs, vous pouvez procéder à la mise en œuvre complète du mappage normal.

Cartographie normale dans l'espace tangent

Vous devez d'abord créer une matrice TBN dans les shaders. À cette fin, nous allons transférer les vecteurs tangents et bi-tangents pré-préparés au shader de vertex à travers les attributs de vertex:

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; 

Dans le code du vertex shader lui-même, nous formons directement la matrice:

 void main() { [...] vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); mat3 TBN = mat3(T, B, N) } 

Dans le code ci-dessus, nous convertissons d'abord tous les vecteurs de la base de l'espace tangent en un système de coordonnées dans lequel nous sommes à l'aise de travailler - dans ce cas, c'est le système de coordonnées mondial et nous multiplions les vecteurs par le modèle de matrice modèle . Ensuite, nous créons la matrice TBN elle-même en passant simplement les trois vecteurs correspondants à un constructeur de type mat3 . Veuillez noter que pour l'exactitude de l'ordre de calcul, il est nécessaire de multiplier les vecteurs non pas par la matrice du modèle, mais par la matrice normale, car nous ne nous intéressons qu'à l'orientation des vecteurs, mais pas à leur déplacement ou à leur mise à l'échelle

À strictement parler, il n'est pas nécessaire de transférer le vecteur bi-tangent au shader.
Puisque le triple des vecteurs TBN est mutuellement perpendiculaire, la bi-tangente peut être trouvée dans le shader par multiplication vectorielle:

  vec3 B = cross(N, T) 

Ainsi, la matrice TBN est reçue, comment l'utilisons-nous? En fait, il existe deux approches pour son utilisation dans la cartographie normale:

1. Utilisez la matrice TBN pour transformer tous les vecteurs nécessaires de la tangente à l'espace mondial. Transférez les résultats dans le fragment shader, où, en utilisant également la matrice, transformez le vecteur de la carte normale en espace mondial. En conséquence, le vecteur normal sera dans l'espace où tout l'éclairage est calculé.
2. Prenez la matrice inverse en TBN et convertissez tous les vecteurs nécessaires de l'espace mondial en tangente. C'est-à-dire utilisez cette matrice pour transformer les vecteurs impliqués dans les calculs d'éclairage en espace tangent. Dans ce cas, le vecteur normal reste également dans le même espace que les autres participants au calcul de l'éclairage.

Regardons la première option. Le vecteur normal de la texture correspondante est spécifié dans l'espace tangent, tandis que les autres vecteurs utilisés dans le calcul de l'éclairage sont définis dans l'espace du monde. En passant la matrice TBN au fragment shader, nous pourrions transformer le vecteur normal obtenu par échantillonnage de la texture de l'espace tangent au monde, assurant l'unité des systèmes de coordonnées pour tous les éléments du calcul d'éclairage. Dans ce cas, tous les calculs (en particulier les multiplications vectorielles scalaires) seront corrects.

Le transfert de la matrice TBN se fait de la manière la plus simple:

 out VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } vs_out; void main() { [...] vs_out.TBN = mat3(T, B, N); } 

Dans le code de shader de fragment, respectivement, nous définissons une variable d'entrée de type mat3:

 in VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } fs_in; 

Ayant la matrice sous la main, vous pouvez spécifier le code pour obtenir la normale par l'expression de la traduction de la tangente à l'espace mondial:

 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); normal = normalize(fs_in.TBN * normal); 

Étant donné que la normale résultante est désormais définie dans l'espace mondial, il n'est pas nécessaire de changer quoi que ce soit d'autre dans le code du shader. Calculs d'éclairage, et supposons donc un vecteur normal donné en coordonnées universelles.

Examinons également la deuxième approche.Cela nécessitera l'obtention de la matrice TBN inverse, ainsi que le transfert de tous les vecteurs impliqués dans le calcul d'éclairage du système de coordonnées universelles vers celui qui correspond aux vecteurs normaux obtenus à partir de la texture - la tangente. Dans ce cas, la formation de la matrice TBN reste inchangée, mais avant de passer au fragment shader nous devons obtenir la matrice inverse:

 vs_out.TBN = transpose(mat3(T, B, N)); 

Notez que la fonction transpose () est utilisée à la place de inverse () . Une telle substitution est vraie, car pour les matrices orthogonales (où tous les axes sont représentés par des vecteurs unitaires perpendiculaires), l'obtention de la matrice inverse donne un résultat identique à la transposition. Et cela est très utile, car, dans le cas général, le calcul de la matrice inverse est une tâche beaucoup plus coûteuse en termes de calcul que la transposition.

Dans le code de shader de fragment, nous ne convertirons pas le vecteur normal, nous convertirons plutôt d'autres vecteurs importants du système de coordonnées mondial en tangente, à savoir lightDir et viewDir. Cette solution rassemble également tous les éléments des calculs dans un seul système de coordonnées, cette fois la tangente.

 void main() { vec3 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos); vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos); [...] } 

La deuxième approche semble prendre plus de temps et nécessite plus de multiplications matricielles dans le fragment shader (ce qui affecte considérablement les performances). Pourquoi avons-nous même commencé à le démonter?
Le fait est que la traduction de vecteurs des coordonnées du monde en tangentes offre un avantage supplémentaire: en fait, nous pouvons déplacer le code de transformation entier du fragment au vertex shader! Cette approche fonctionne car lightPos et viewPos ne changent pas de fragment en fragment, et la valeur est fs_in.FragPosnous pouvons également traduire en espace tangent dans le vertex shader, la valeur interpolée à l'entrée du fragment shader sera tout à fait correcte. Ainsi, pour la deuxième approche, il n'est pas nécessaire de traduire tous ces vecteurs dans l'espace tangent dans le code de shader de fragment, tandis que le premier l'exige - car la normale est unique pour chaque fragment.

En conséquence, nous nous éloignons du transfert de la matrice inverse de TBN au fragment shader et lui passons plutôt le vecteur de position du sommet, de la source lumineuse et de l'observateur dans l'espace tangent. Nous allons donc nous débarrasser des multiplications de matrice coûteuses dans le fragment shader, ce qui sera une optimisation importante, car le vertex shader est exécuté beaucoup moins souvent. C'est cet avantage qui place la deuxième approche dans la catégorie d'utilisation préférée dans la plupart des cas.

 out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform vec3 lightPos; uniform vec3 viewPos; [...] void main() { [...] mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0)); 

Dans le fragment shader, nous passons à l'utilisation de nouvelles variables d'entrée dans les calculs d'éclairage dans l'espace tangent. Puisque les normales sont définies conditionnellement dans cet espace, tous les calculs restent corrects.
Maintenant que tous les calculs de cartographie normaux sont effectués dans un espace tangent, nous pouvons changer l'orientation de la surface de test dans l'application comme nous le voulons et l'éclairage restera correct:

 glm::mat4 model(1.0f); model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); shader.setMat4("model", model); RenderQuad(); 

En effet, extérieurement tout se passe comme il se doit:


Les sources sont ici .

Objets complexes

Nous avons donc compris comment effectuer une cartographie normale dans un espace tangent et comment calculer indépendamment les vecteurs tangents et tangents pour cela. Heureusement, un tel calcul manuel n'est pas si souvent une tâche: pour la plupart, ce code est implémenté par les développeurs quelque part dans les entrailles du chargeur de modèle. Dans notre cas, cela est vrai pour le chargeur Assimp utilisé .

Assimp fournit un indicateur d'option très utile lors du chargement de modèles: aiProcess_CalcTangentSpace . Lorsqu'elle est passée à la fonction ReadFile () , la bibliothèque elle-même calculera les lignes tangentes et bi-tangentes lisses pour chacun des sommets chargés - un processus similaire à celui discuté ici.

 const aiScene *scene = importer.ReadFile( path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace ); 

Après cela, vous pouvez accéder directement aux tangentes calculées:

 vector.x = mesh->mTangents[i].x; vector.y = mesh->mTangents[i].y; vector.z = mesh->mTangents[i].z; vertex.Tangent = vector; 

Vous devrez également mettre à jour le code de téléchargement pour prendre en compte la réception de cartes normales pour les modèles texturés. Le format Wavefront Object (.obj) exporte les cartes normales de telle manière que l'indicateur Assimp aiTextureType_NORMAL ne garantit pas que ces cartes se chargent correctement, tandis que tout fonctionne correctement avec l'indicateur aiTextureType_HEIGHT . Par conséquent, personnellement, je charge généralement les cartes normales de la manière suivante:

 vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal"); 

Bien entendu, cette approche peut ne pas convenir à d'autres formats de description de modèle et types de fichiers. Je note également que la définition de l'indicateur aiProcess_CalcTangentSpace ne fonctionne pas toujours. Nous savons que le calcul des tangentes est basé sur les coordonnées de texture, cependant, souvent les auteurs de modèles appliquent diverses astuces aux coordonnées de texture, ce qui rompt le calcul des tangentes. Ainsi, une image miroir des coordonnées de texture est souvent utilisée pour les modèles à texture symétrique. Si le fait de refléter n'est pas pris en compte, alors le calcul des tangentes sera incorrect. Assimp ne fait pas cette comptabilité. Le modèle de nanosuit familier ici ne convient pas pour la démonstration, car il utilise également la mise en miroir.

Mais avec un modèle correctement texturé utilisant des cartes normales et spéculaires, l'application de test donne un très bon résultat:


Comme vous pouvez le voir, l'utilisation de la cartographie normale fournit une augmentation tangible des détails et est bon marché en termes de coûts de performance.

N'oubliez pas que l'utilisation d'un mappage normal peut aider à améliorer les performances d'une scène particulière. Sans son utilisation, la réalisation des détails du modèle n'est possible qu'en augmentant la densité du maillage polygonal, le maillage. Mais cette technique vous permet d'atteindre visuellement le même niveau de détail pour les maillages low-poly. Ci-dessous, vous pouvez voir une comparaison de ces deux approches:


Le niveau de détail sur le modèle à haute poly et sur le modèle à faible poly utilisant la cartographie normale est pratiquement indiscernable. Cette technique est donc un excellent moyen de remplacer les modèles à haute poly dans la scène par des modèles simplifiés avec pratiquement aucune perte de qualité visuelle.

Dernier commentaire

Il y a un autre détail technique concernant la cartographie normale, qui améliore un peu la qualité avec peu ou pas de coût supplémentaire.

Dans les cas où les tangentes sont calculées pour des maillages grands et complexes avec un nombre significatif de sommets appartenant à plusieurs triangles, les vecteurs tangents sont généralement moyennés pour obtenir un résultat de mappage normal lisse et visuellement agréable. Cependant, cela crée un problème: après la moyenne, le triple des vecteurs TBN peut perdre la perpendicularité mutuelle, ce qui signifie également la perte d'orthogonalité pour la matrice TBN. Dans le cas général, le résultat d'une cartographie normale obtenue à partir d'une matrice non orthogonale n'est que légèrement incorrect, mais on peut encore l'améliorer.

Pour ce faire, il suffit d'appliquer une méthode mathématique simple:Processus de Gram-Schmidt ou ré-orthogonalisation de notre triple de vecteurs TBN. Dans le code du vertex shader:

 vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); // - T  N T = normalize(T - dot(T, N) * N); //    B    T  N vec3 B = cross(N, T); mat3 TBN = mat3(T, B, N) 

Cet amendement, bien que modeste, améliore la qualité de la cartographie normale en échange de faibles frais généraux. Si vous êtes intéressé par les détails de cette procédure, vous pouvez regarder la dernière partie de la vidéo Mathématiques cartographiques normales, dont le lien est donné ci-dessous.

Ressources supplémentaires

• Tutoriel 26: Cartographie normale : une leçon sur la cartographie normale d' ogldev .
• Fonctionnement du mappage normal : didacticiel vidéo expliquant les bases du mappage normal de TheBennyBox .
• Mathématiques de cartographie normale : un film lié à la précédente qui explique les mathématiques utilisées dans la méthode de cartographie normale, également de TheBennyBox .
• Tutoriel 13: Cartographie normale : une autre leçon de opengl-tutorial.org .

PS : Nous avons un télégramme conf pour la coordination des transferts. Si vous avez un sérieux désir d'aider à la traduction, alors vous êtes les bienvenus!