La dynamique du vol vertical d'un avion plus léger que l'air

Présentation

La détermination de la vitesse de montée et de descente des avions plus légers que l'air (LALV) à ce jour est presque une tâche importante qui se pose dans la conception de tels dispositifs.

Un grand nombre de publications sont consacrées au LALF, par exemple, seulement sur notre ressource sont deux articles très intéressants [1,2] liés à l'histoire du développement en utilisant des modèles spécifiques de dirigeables et de stratostats comme exemples. Cependant, il existe très peu de calculs de la dynamique du vol vertical de tels appareils, permettant au moins de déterminer grossièrement la vitesse de montée et de descente des ALPC.

La dernière déclaration nécessite une certaine explication, car un lecteur expérimenté se souvient du cours de physique de l'école, dans lequel les problèmes de hauteur d'élévation et d'autres paramètres des ballons remplis de gaz plus légers que l'air ou par l'air lui-même chauffé pendant le vol ont été résolus.

Toutes ces tâches étaient basées sur l'égalité de deux forces: la force de poids et la force de flottabilité. Les gaz ont été considérés comme idéaux et leurs paramètres ont été calculés selon la loi de Mendeleev Clapeyron. Cependant, même un simple calcul de la troisième force de résistance à l'air conduit déjà à un système d'équations différentielles, qui ne peut pas être résolu analytiquement. Il est également nécessaire de prendre en compte la variation de la densité de l'air atmosphérique avec la hauteur de montée et la température.

De plus, si vous devez considérer non seulement la montée, mais aussi le gel de la balle et sa descente au sol, ce n'est pas du tout une tâche pour les enfants. J'espère que l'examen de la solution d'un problème similaire au moyen de Python contribuera non seulement à l'expansion des connaissances en physique, mais aussi à la vulgarisation du langage de programmation Python lui-même. Ce que j'essaie de faire dans mes publications sur cette ressource.

Un modèle mathématique du vol d'un LALV avec une coquille en forme de boule dont le volume ne change pas avec la hauteur

Nous nous limitons à considérer le mouvement de son centre de masse sous l'action des forces suivantes: gravité ( G ), force d'Archimède ( Fa ) et force de traînée aérodynamique ( Fc ). Nous écrivons les relations pour déterminer les forces à travers les paramètres de mouvement et l'environnement de l'air [3]:





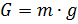
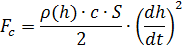
Dans les formules ci-dessus, la notation est utilisée: h est la hauteur de la balle, dh / dt est la vitesse verticale, m est la masse, g est l'accélération de la gravité, W est le volume de la balle, c est le coefficient de traînée, S est la zone de résistance caractéristique (zone médiane).
On suppose que la dépendance de la densité de l'air à la hauteur est exponentielle:



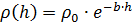
où $$$ρ_0$ - densité de l'air à hauteur nulle, b - coefficient. La gravité est dirigée vers le bas, la force d'Archimède est dirigée vers le haut et la force de traînée aérodynamique est toujours dirigée «contre le mouvement». Par conséquent, l'inclusion correcte de cette force dans les équations du mouvement nécessite l'introduction d'un facteur $$$-sing (dh / dt)$ .

Cependant, pour notre propos, ce fait n'est pas d'une importance fondamentale, et nous nous limitons à ne considérer que le stade de l'élévation du ballon, lorsque la force de traînée aérodynamique est dirigée vers le bas et, par conséquent, sera prise en compte dans les équations de mouvement avec un signe moins. Maintenant, l'équation du mouvement peut s'écrire:

, (1)

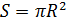
De plus, supposons que le ballon soit un corps homogène de rayon R de densité $$$ρ_b$ . Ensuite, la taille de la zone qui détermine sa traînée aérodynamique est définie comme volume comme et la masse, respectivement, .

Maintenant, il est clair que chaque terme de l'équation (1) contient S. comme facteur. Par conséquent, chaque terme de l'équation du mouvement peut être réduit d'un facteur S. L'équation elle-même prendra la forme:

, (2)

Nous introduisons la notation suivante:

;
;

et réécrire (2) sous la forme du système d'équations non linéaires suivant:

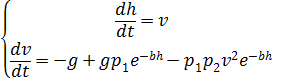
, (3)

Influence sur la vitesse et la hauteur de l'élévation de la température de l'air du LALV

Pour ce faire, nous résolvons d'abord le système (3) en utilisant la relation suivante pour la dépendance de la densité de l'air atmosphérique sur la hauteur sans tenir compte de la température:



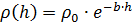
Reprenons la solution du système (3), mais en utilisant la relation pour la dépendance de la densité de l'air à l'altitude et à la température:



où: b = 0,000125 est une constante associée à une densité de l'air de 1 / m;
a = 0,0065 est une constante liée à la température de l'air en K / m.
$$$T_0 = 300 K$ - température au niveau de la mer.


Nous obtenons:



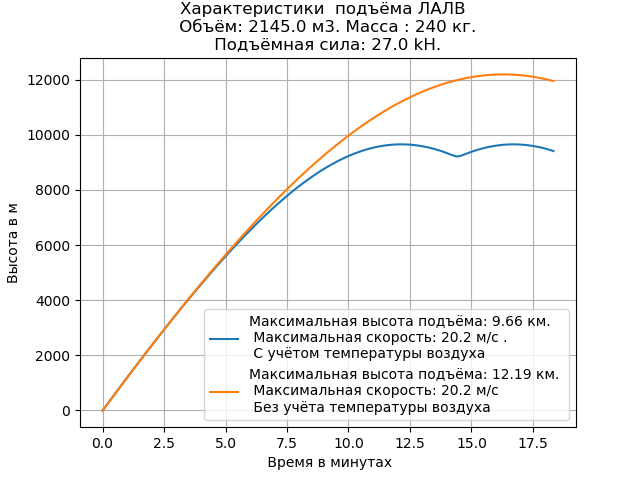
La valeur calculée de la hauteur de l'ascenseur LALV, compte tenu de la température, est inférieure à celle sans. La vitesse de levage de l'appareil reste inchangée.

Détermination des caractéristiques de toutes les phases du vol SALV du début à l'atterrissage

Pour construire le programme de vol LALV, considérez les conditions pour les périodes suivantes:

Rise - ;
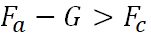
Accrochez - ;
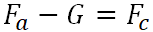
Atterrissage - .


Nous obtenons:



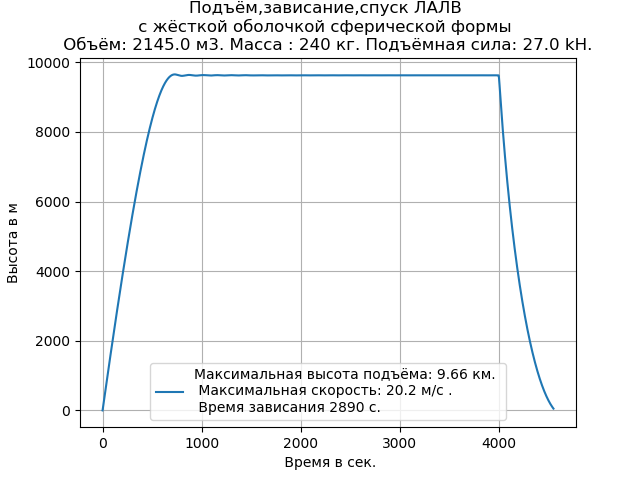
Comme il ressort du graphique et de la liste du programme, pour mener une expérience de calcul, il suffit d'entrer les données initiales nécessaires.

Un modèle mathématique du vol d'un LALV à coque dont le volume varie avec la hauteur

Ces LALV comprennent des stratostats. Le ballon stratosphérique ne peut pas être complètement gonflé à l'hélium, ce qui lui confère une force de levage maximale, qui transformera la forme de sa coque en ballon. Une telle balle à haute altitude peut éclater en raison de la différence accrue de pressions internes et externes.

Pour ces raisons, pour calculer la hauteur de levage maximale atteignable, deux valeurs de son volume sont introduites: la Vmin minimale et la Vmax maximale, respectivement. Compte tenu des variables introduites et de la dépendance de la densité de l'air sur la hauteur, les rapports de la force de flottabilité Fa et de la force de gravité prennent la forme

, (4)

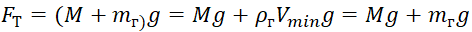
, (5)

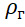
où: M est la masse de la coque et de l'équipement du ballon stratosphérique; Est la densité d'hélium.

En égalisant les relations (4) et (5), en supposant que le volume de la coque V est fonction de la hauteur du LALV, on obtient le rapport:

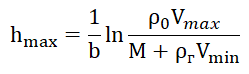
. (6)

Les valeurs numériques des paramètres inclus dans la relation (6) sont données dans la liste pour la construction d'un graphique, qui n'est donnée que dans le but indiqué.


Nous obtenons:



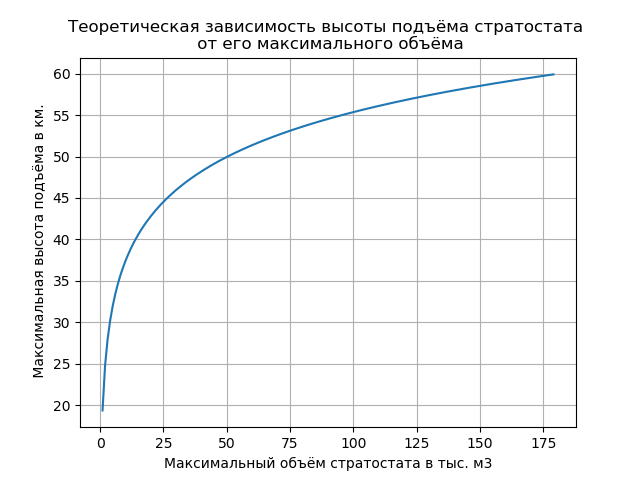
En modifiant les paramètres LALV répertoriés dans la liste des programmes, vous pouvez obtenir le graphique donné et sélectionner le volume de shell maximum requis lors de la conception. Le raffinement des résultats est effectué en utilisant une vaste expérience dans la création de tels dispositifs.

Conclusions:

1. On obtient des modèles mathématiques de deux types d'avions plus légers que l'air, qui permettent des expériences de calcul pour évaluer les paramètres de tels appareils dans des conditions idéalisées de l'environnement aérien.
   
2. Le schéma proposé en plusieurs étapes pour résoudre numériquement le système d'équations différentielles nous permet d'obtenir la trajectoire verticale d'un avion plus léger que l'air aux stades de vol stationnaire et d'abaissement.
   

Les références

1. Quelques mots sur les dirigeables
   
2. En route vers l'espace. Stratostats
   
3. Ryzhikov Yu.I. Fortran moderne. - Saint-Pétersbourg: Crown print, 2004 .-- 288 p.