Les mathématiciens ont réfuté une hypothèse conçue pour sauver les trous noirs

Les mathématiciens ont réfuté l'hypothèse de l'existence d'un principe fort de censure cosmique. Leurs travaux répondent à l'une des questions les plus importantes de l'étude de la théorie générale de la relativité et modifient notre façon de parler de l'espace-temps.

Près de 40 ans après sa formulation, les mathématiciens se sont prononcés sur l'une des questions les plus importantes de l'étude de la théorie générale de la relativité. Dans un article publié en ligne l'automne dernier, les mathématiciens Michalis Dafermos et Jonathan Luck ont prouvé que la forme forte du principe de censure cosmique relative à l'étrange structure des trous noirs est incorrecte.

«Personnellement, je considère ce travail comme une réalisation incroyable - un saut qualitatif dans notre compréhension de la relativité générale», m'a écrit Igor Rodnyansky , mathématicien de l'Université de Princeton.

Une forme puissante du principe de censure spatiale a été proposée en 1979 par le physicien influent Roger Penrose. C'était un moyen d'échapper au piège. Par des décennies de relativité générale, Albert Einstein a statué comme la meilleure description scientifique des phénomènes à grande échelle de l'univers. Cependant, les réalisations mathématiques des années 1960 ont montré que les équations d'Einstein trouvaient des incohérences désagréables lorsqu'elles étaient appliquées aux trous noirs. Penrose croyait que si son principe fort de censure cosmique est vrai, alors le manque de prévisibilité peut être ignoré, le considérant comme une caractéristique mathématique, et non une véritable description du monde physique.

"Penrose a émis une hypothèse qui a essentiellement tenté de se débarrasser comme par magie de ces comportements désagréables", a déclaré Dafermos, mathématicien à Princeton.

Une nouvelle œuvre brise le rêve de Penrose. En même temps, elle remplit ses ambitions d'une autre manière, montrant que sa compréhension intuitive de l'intérieur du trou noir était correcte, tout simplement pas pour les raisons qu'il soupçonnait.

Le péché mortel de la relativité

En physique classique, l'univers est prévisible. Si vous connaissez les lois régissant le système physique et son état initial, vous devriez pouvoir suivre son développement à l'infini. Cette maxime fonctionne que vous essayiez d'utiliser les lois de Newton pour prédire la position future d'une boule de billard, l'équation de Maxwell pour décrire le champ électromagnétique ou le GRT d'Einstein pour prédire l'évolution de la forme espace-temps. "C'est le principe de base de toute la physique classique, qui remonte à la mécanique newtonienne", a déclaré Demetrios Hristodulu , mathématicien de l'ETH Zurich et spécialiste de premier plan dans l'étude des équations d'Einstein. "L'évolution peut être déterminée sur la base des données initiales."

Mais dans les années 1960, les mathématiciens ont découvert un scénario physique dans lequel les équations du champ gravitationnel d'Einstein - formant le noyau de son GR - cessent de décrire un univers prévisible. Les mathématiciens et les physiciens ont remarqué que quelque chose ne va pas quand ils ont modélisé l'évolution de l'espace-temps à l'intérieur d'un trou noir en rotation.

Pour comprendre ce qui s'est mal passé, imaginez-vous tomber dans un trou noir. D'abord, vous traversez l'horizon des événements, le point de non-retour (même si pour vous ce n'est pas différent de l'espace ordinaire). Ici, les équations d'Einstein fonctionnent toujours comme elles le devraient, donnant une prévision déterministe unique de la façon dont l'espace-temps changera à l'avenir.


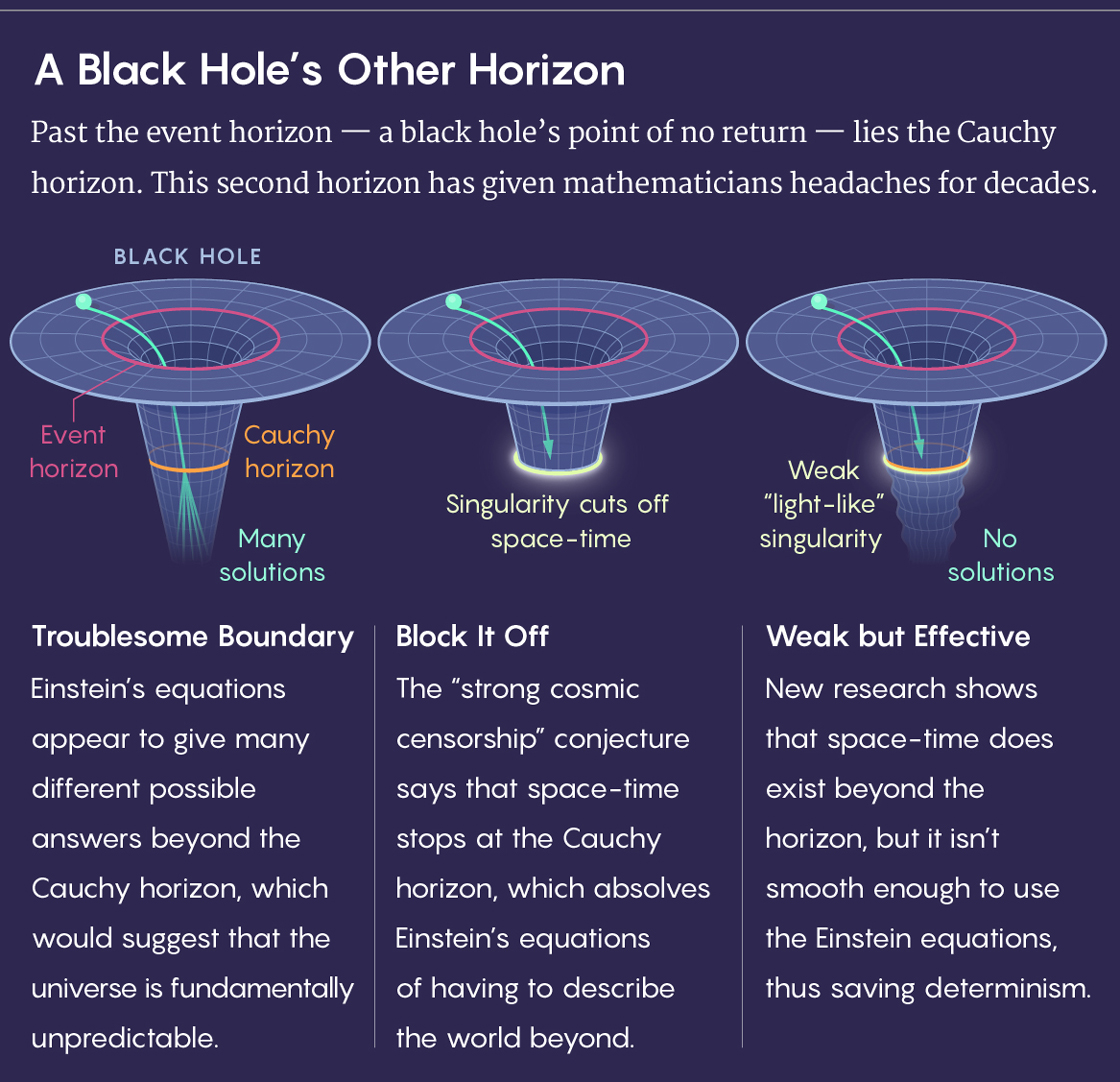Au-delà du point de non-retour de la BH se trouve le deuxième horizon - l'horizon de Cauchy . Les équations d'Einstein offrent de nombreuses options de solutions au-delà de l'horizon de Cauchy, ce qui signifierait que l'Univers est fondamentalement imprévisible.

Le principe fort de la censure cosmique dit que l’espace-temps se termine à l’horizon de Cauchy, de sorte que les équations d’Einstein n’ont pas besoin de décrire davantage le monde.
Mais une nouvelle étude montre qu'au-delà de cet horizon, il y a l'espace-temps, mais il n'est pas assez lisse pour utiliser les équations d'Einstein - cela préserve la prévisibilité.

Si vous continuez votre voyage à l'intérieur de BH, vous finirez par traverser un autre horizon, connu sous le nom d'horizon de Cauchy. Et puis tout devient fou. Les équations d'Einstein commencent à produire de nombreuses variations de l'espace-temps. Ils diffèrent tous les uns des autres, mais satisfont aux équations. La théorie ne peut pas dire quelle option sera correcte. Pour la théorie physique, c'est un péché mortel.

«La perte de prévisibilité que nous semblons constater en relativité générale a été très désagréable», a déclaré Eric Poisson , physicien à l'Université de Guelph au Canada.

Roger Penrose a proposé le principe fort de la censure cosmique pour restaurer la prévisibilité dans les équations d'Einstein. Il dit que l'horizon de Cauchy est une construction purement mathématique. Il pourrait exister dans un scénario idéal dans lequel il n'y a rien dans l'Univers sauf un seul trou noir rotatif, mais il ne peut pas exister dans la réalité.

Selon lui, la raison en est que l'horizon de Cauchy est instable. Il a dit que toute onde gravitationnelle qui la traverserait devrait provoquer son effondrement en une singularité - en une section de densité infinie, déchirant l'espace-temps. Puisque l'Univers réel est plein de telles vagues, l'horizon de Cauchy ne devrait pas apparaître dans la nature.

Par conséquent, cela n'a aucun sens de se demander ce qui arrive à l'espace-temps au-delà de l'horizon de Cauchy, puisque l'espace-temps, tel que décrit dans le cadre de GR, cesse d'exister. "C'est une façon de sortir de ce puzzle", a déclaré Dafermos.

Mais ce nouveau travail montre que la frontière espace-temps définie par l'horizon de Cauchy a moins à voir avec la singularité que Penrose ne l'imaginait.

Sauvez le trou noir

Dafermos et Luck, un mathématicien de Stanford, ont prouvé que la situation à l'horizon Cauchy n'est pas si simple. Leur travail réfute astucieusement la lettre de la déclaration initiale de Penrose sur la censure spatiale, mais ne rejette pas complètement son esprit.

Sur la base de méthodes développées il y a dix ans par Christodoulou, ancien mentor de Dafermos à l'institut, le couple a montré que l'horizon de Cauchy pouvait en effet former une singularité, mais pas ce que Penrose attendait. La singularité de leur travail n'est pas aussi nette que celle de Penrose - ils ont trouvé une singularité faible et «légère» où ils s'attendaient à en trouver une «spatiale». Une forme de singularité plus faible attire le tissu de l'espace-temps, mais ne le déchire pas. «Notre théorème dit que les observateurs traversant l'horizon de Cauchy ne sont pas déchirés par les forces de marée. Ils peuvent sentir l'injection, mais ils ne se déchireront pas », a déclaré Dafermos dans le courrier.

Étant donné que la singularité qui se forme à l'horizon de Cauchy est plus douce que celle qui prédit le principe fort de la censure cosmique, GTR n'interdit pas de prédire ce qui se passe à l'intérieur. "Il est toujours logique de déterminer l'horizon de Cauchy, parce que nous pouvons, si nous le souhaitons, étendre continuellement l'espace-temps au-delà", a déclaré Harvey Rial , physicien à l'Université de Cambridge.

Dafermos et Luck ont ​​prouvé que l'espace-temps s'étend au-delà de l'horizon de Cauchy. Ils ont également prouvé qu’à partir d’un même point de départ, cela peut se poursuivre de différentes manières. Au-delà de l'horizon, «il existe de nombreuses suites de ce type qui peuvent être envisagées, et il n'y a aucune raison de préférer l'une d'entre elles à l'autre», a déclaré Dafermos.

Cependant - et c'est là que réside l'astuce de leur travail - ces extensions non uniques de l'espace-temps ne signifient pas que les équations d'Einstein se brisent au-delà de l'horizon.

Les équations d'Einstein fonctionnent en mesurant les changements d'espace-temps dans le temps. En termes mathématiques, il est nécessaire de prendre des dérivées de la configuration initiale espace-temps. Et pour prendre la dérivée, il faut que l'espace-temps soit suffisamment «lisse» - sans discontinuités. Dafermos et Luck montrent que bien que l'espace-temps existe au-delà de l'horizon de Cauchy, cet espace-temps étendu ne sera pas suffisamment lisse pour satisfaire les équations d'Einstein. Par conséquent, bien que le principe fort de la censure cosmique ait été réfuté, les équations sont exemptes de la honte d'émettre des solutions non uniques.

«Il est logique de parler de l'horizon Cauchy; cependant, vous ne pouvez pas passer pour cela dans le cadre de la résolution des équations d'Einstein, a déclaré Rial. "Je pense qu'ils ont fourni des preuves convaincantes que c'est le cas."

Ce résultat peut être imaginé comme un compromis désagréable: bien qu'il soit possible de continuer l'espace-temps au-delà de l'horizon de Cauchy, les équations d'Einstein ne peuvent pas être résolues. Mais c'est précisément le fait de l'existence d'un tel compromis qui rend le travail de Dafermos et Luck si intéressant.

"En fait, un nouveau phénomène a été découvert dans les équations d'Einstein", a déclaré Rodnyansky.