AI, cours pratique. Vue d'ensemble des réseaux de neurones pour la classification d'images

Cet article fournit un aperçu théorique accessible des réseaux de neurones convolutifs (CNN) et explique leur application au problème de classification d'images.

Approche commune: pas d'apprentissage en profondeur

Le terme "traitement d'image" se réfère à une large classe de tâches pour lesquelles les données d'entrée sont des images, et la sortie peut être soit des images soit des ensembles de caractéristiques caractéristiques associées. Il existe de nombreuses options: classification, segmentation, annotation, détection d'objets, etc. Dans cet article, nous examinons la classification des images, non seulement parce que c'est la tâche la plus simple, mais aussi parce qu'elle sous-tend de nombreuses autres tâches.

L'approche générale de la classification des images comprend les deux étapes suivantes:

1. Génération de caractéristiques importantes de l'image.
2. Classification d'une image en fonction de ses attributs.

La séquence d'opérations courante utilise des modèles simples tels que le Perceptron multicouche (MLP), la Machine à vecteurs de support (SVM), la méthode k des voisins les plus proches et la régression logistique en plus des fonctionnalités créées manuellement. Les attributs sont générés à l'aide de diverses transformations (par exemple, la détection des niveaux de gris et des seuils) et des descripteurs, par exemple, l'histogramme des gradients orientés ( HOG ) ou les transformations SIFT (invariable à l'échelle), et etc.

La principale limitation des méthodes généralement acceptées est la participation d'un expert qui choisit un ensemble et une séquence d'étapes pour générer des fonctionnalités.

Au fil du temps, il a été constaté que la plupart des techniques de génération d'entités peuvent être généralisées à l'aide de noyaux (filtres) - de petites matrices (généralement de taille 5 × 5), qui sont des convolutions des images originales. La convolution peut être considérée comme un processus séquentiel en deux étapes:

1. Passez le même noyau fixe dans toute l'image source.
2. À chaque étape, calculez le produit scalaire du noyau et l'image d'origine à l'emplacement actuel du noyau.

Le résultat de la convolution de l'image et du noyau est appelé une carte de caractéristiques.
Une explication mathématiquement plus rigoureuse est donnée dans le chapitre pertinent du livre récemment publié, Deep Learning, par I. Goodfellow, I. Benjio et A. Courville.


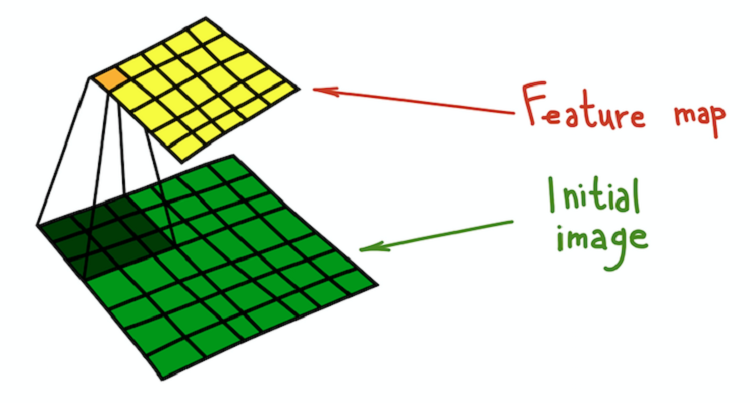Processus de convolution du noyau (vert foncé) avec l'image d'origine (vert), à la suite de quoi une carte des caractéristiques est obtenue (jaune).

Un exemple simple d'une transformation qui peut être effectuée avec des filtres est le flou d'une image. Prenez un filtre composé de toutes les unités. Il calcule la moyenne du voisinage déterminée par le filtre. Dans ce cas, le quartier est une section carrée, mais il peut être cruciforme ou autre. La moyenne conduit à la perte d'informations sur la position exacte des objets, brouillant ainsi l'image entière. Une explication intuitive similaire peut être donnée pour tout filtre créé manuellement.


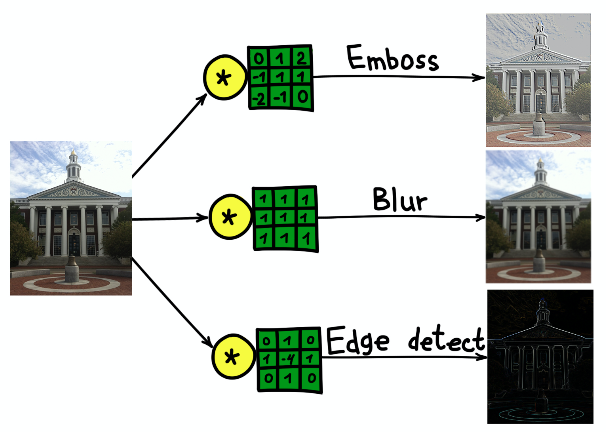Le résultat de la convolution de l'image du bâtiment de l'Université Harvard avec trois noyaux différents.

Réseaux de neurones convolutifs

L'approche convolutionnelle de la classification des images présente un certain nombre d'inconvénients importants:

• Un processus en plusieurs étapes au lieu d'une séquence de bout en bout.
• Les filtres sont un excellent outil de généralisation, mais ce sont des matrices fixes. Comment choisir les poids dans les filtres?

Heureusement, des filtres apprenants ont été inventés, qui sont le principe de base qui sous-tend CNN. Le principe est simple: nous formerons les filtres appliqués à la description des images afin de remplir au mieux leur tâche.

CNN n'a pas d'inventeur, mais l'un des premiers cas de leur application est LeNet-5 * dans l'ouvrage " Gradient-based Learning Applied to Document Recognition" de I. LeCun et d'autres auteurs.

CNN tue deux oiseaux avec une pierre: aucune définition préliminaire des filtres n'est nécessaire et le processus d'apprentissage devient de bout en bout. Une architecture CNN typique se compose des parties suivantes:

• Couches convolutives
• Sous-échantillonnage des couches
• Couches denses (entièrement connectées)

Examinons chaque partie plus en détail.

Couches convolutives

La couche convolutionnelle est le principal élément structurel de CNN. La couche convolutionnelle présente un ensemble de caractéristiques:
Connectivité locale (clairsemée) . Dans les couches denses, chaque neurone est connecté à chaque neurone de la couche précédente (ils étaient donc appelés denses). Dans la couche convolutionnelle, chaque neurone n'est connecté qu'à une petite partie des neurones de la couche précédente.


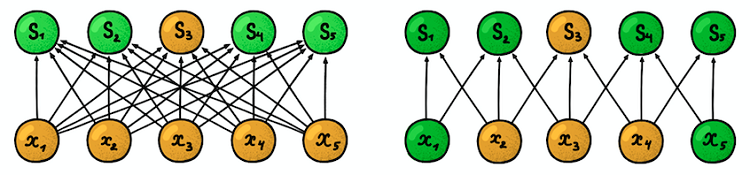Un exemple de réseau neuronal unidimensionnel. (à gauche) Connexion de neurones dans un réseau dense typique, (à droite) Caractérisation de la connectivité locale inhérente à la couche convolutionnelle. Images prises de I. Goodfellow et d'autres par Deep Learning

La taille de la zone à laquelle le neurone est connecté est appelée taille du filtre (la longueur du filtre dans le cas de données unidimensionnelles, par exemple, des séries chronologiques, ou la largeur / hauteur dans le cas de données bidimensionnelles, par exemple, des images). Dans la figure de droite, la taille du filtre est 3. Les poids avec lesquels la connexion est établie sont appelés un filtre (un vecteur dans le cas de données unidimensionnelles et une matrice pour des données bidimensionnelles). Le pas est la distance parcourue par le filtre sur les données (dans la figure de droite, le pas est 1). L'idée de connectivité locale n'est rien de plus qu'un noyau qui déplace une étape. Chaque neurone de niveau convolutionnel représente et met en œuvre une position spécifique du noyau glissant le long de l'image d'origine.


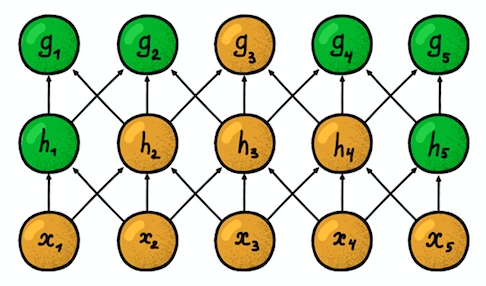Deux couches convolutives unidimensionnelles adjacentes

Une autre propriété importante est la zone dite de susceptibilité . Il reflète le nombre de positions du signal d'origine que le neurone actuel peut «voir». Par exemple, la zone de susceptibilité de la première couche réseau, représentée sur la figure, est égale à la taille du filtre 3, car chaque neurone est connecté à seulement trois neurones du signal d'origine. Cependant, sur la deuxième couche, la zone de susceptibilité est déjà de 5, puisque le neurone de la deuxième couche regroupe trois neurones de la première couche, dont chacun a une zone de susceptibilité 3. Avec une profondeur croissante, la zone de susceptibilité croît linéairement.

Paramètres partagés . Rappelons que dans le traitement d'image classique, le même noyau glissait sur l'image entière. La même idée s'applique ici. Nous fixons uniquement la taille du filtre de poids pour une couche et nous appliquerons ces poids à tous les neurones de la couche. Cela revient à faire glisser le même noyau sur toute l'image. Mais la question peut se poser: comment apprendre quelque chose avec un si petit nombre de paramètres?


Les flèches foncées représentent les mêmes poids. (à gauche) MLP régulier, où chaque facteur de pondération est un paramètre distinct, (à droite) Un exemple de séparation des paramètres, où plusieurs facteurs de pondération indiquent le même paramètre de formation

Structure spatiale . La réponse à cette question est simple: nous formerons plusieurs filtres en une seule couche! Ils sont placés parallèlement les uns aux autres, formant ainsi une nouvelle dimension.

Nous faisons une courte pause et expliquons l'idée présentée par l'exemple d'une image RVB bidimensionnelle de 227 × 227. Notez qu'il s'agit ici d'une image d'entrée à trois canaux, ce qui signifie, en substance, que nous avons trois images d'entrée ou des données d'entrée tridimensionnelles.


La structure spatiale de l'image d'entrée

Nous considérerons les dimensions des canaux comme la profondeur de l'image (notez que ce n'est pas la même que la profondeur des réseaux de neurones, qui est égale au nombre de couches de réseau). La question est de savoir comment déterminer le noyau pour ce cas.


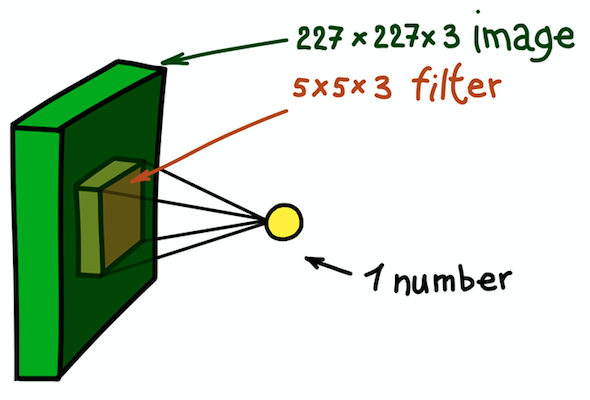
Un exemple d'un noyau bidimensionnel, qui est essentiellement une matrice tridimensionnelle avec une mesure de profondeur supplémentaire. Ce filtre donne une convolution avec l'image; c'est-à-dire glisse sur l'image dans l'espace, calculant des produits scalaires

La réponse est simple, mais pas encore évidente: nous allons également rendre le noyau tridimensionnel. Les deux premières dimensions resteront les mêmes (largeur et hauteur du noyau) et la troisième dimension est toujours égale à la profondeur des données d'entrée.


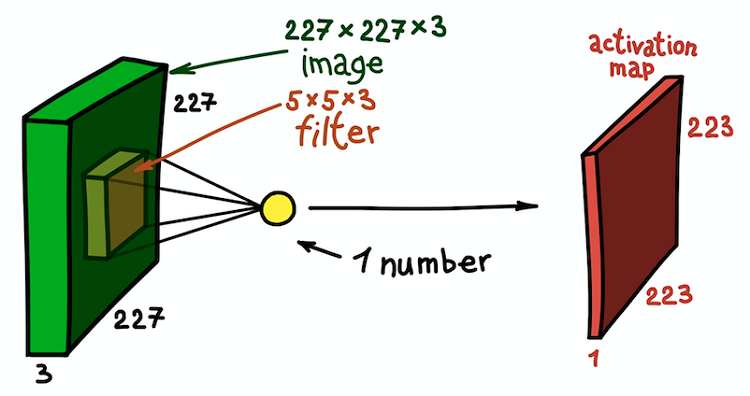
Un exemple d'une étape de convolution spatiale. Le résultat du produit scalaire du filtre et d'une petite partie de l'image 5 × 5 × 3 (c'est-à-dire 5 × 5 × 5 + 1 = 76, la dimension du produit scalaire + décalage) est un nombre

Dans ce cas, toute la section 5 × 5 × 3 de l'image d'origine est transformée en un seul numéro, et l'image tridimensionnelle elle-même sera transformée en une carte d' entités ( carte d'activation ). Une carte des caractéristiques est un ensemble de neurones, chacun calculant sa propre fonction, en tenant compte de deux principes de base discutés ci-dessus: la connectivité locale (chaque neurone n'est associé qu'à une petite partie des données d'entrée) et la séparation des paramètres (tous les neurones utilisent le même filtre). Idéalement, cette carte de caractéristiques sera la même que celle déjà rencontrée dans l'exemple d'un réseau généralement accepté - elle stocke les résultats de la convolution de l'image d'entrée et du filtre.


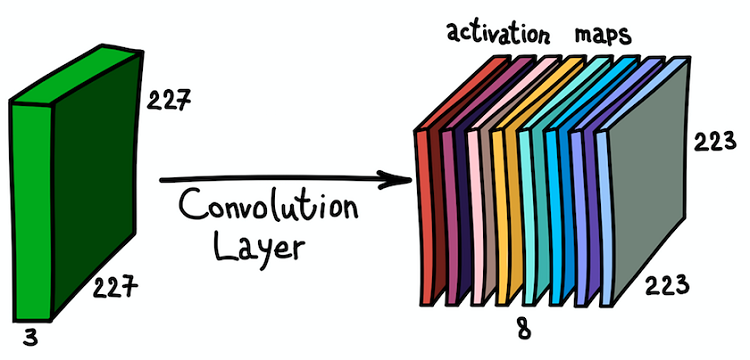
Carte des entités résultant de la convolution du noyau avec toutes les positions spatiales

Notez que la profondeur de la carte d'entités est de 1, car nous n'avons utilisé qu'un seul filtre. Mais rien ne nous empêche d'utiliser plus de filtres; par exemple, 6. Tous interagiront avec les mêmes données d'entrée et fonctionneront indépendamment les uns des autres. Allons un peu plus loin et combinons ces cartes de fonctionnalités. Leurs dimensions spatiales sont les mêmes puisque les dimensions des filtres sont les mêmes. Ainsi, les cartes d'entités collectées ensemble peuvent être considérées comme une nouvelle matrice tridimensionnelle, dont la dimension en profondeur est représentée par des cartes d'entités provenant de différents noyaux. En ce sens, les canaux RVB de l'image d'entrée ne sont autres que les trois cartes d'entités originales.


L'application parallèle de plusieurs filtres à l'image d'entrée et au jeu de cartes d'activation résultant

Une telle compréhension des cartes d'entités et de leur combinaison est très importante, car, après avoir réalisé cela, nous pouvons étendre l'architecture du réseau et installer des couches convolutives les unes sur les autres, augmentant ainsi la zone de susceptibilité et enrichissant notre classificateur.


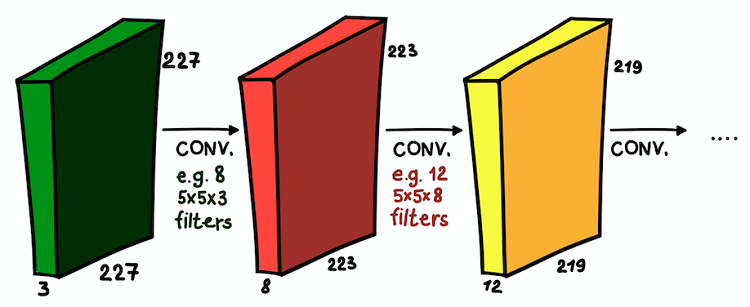Couches convolutives installées les unes sur les autres. Dans chaque couche, la taille des filtres et leur nombre peuvent varier

Nous comprenons maintenant ce qu'est un réseau convolutionnel. L'objectif principal de ces couches est le même qu'avec l'approche généralement acceptée - détecter les signes significatifs de l'image. Et, si dans la première couche ces signes peuvent être très simples (présence de lignes verticales / horizontales), la profondeur du réseau augmente le degré de leur abstraction (présence d'un chien / chat / personne).

Sous-échantillonnage des couches

Les couches convolutives sont le principal élément constitutif de CNN. Mais il y a une autre partie importante et souvent utilisée - ce sont les couches de sous-échantillons. Dans le traitement d'image conventionnel, il n'y a pas d'analogue direct, mais un sous-échantillon peut être considéré comme un autre type de noyau. Qu'est-ce que c'est?


Exemples de sous-échantillonnage. (à gauche) Comment un sous-échantillon modifie la taille spatiale (mais pas le canal!) des tableaux de données, (à droite) Un schéma de base du fonctionnement d'un sous-échantillon

Un sous-échantillon filtre une partie du voisinage de chaque pixel des données d'entrée avec une fonction d'agrégation spécifique, par exemple, maximum, moyenne, etc. Le sous-échantillon est essentiellement le même que la convolution, mais la fonction de combinaison de pixels n'est pas limitée au produit scalaire. Une autre différence importante est que le sous-échantillonnage ne fonctionne que dans la dimension spatiale. Une caractéristique de la couche de sous-échantillonnage est que le pas est généralement égal à la taille du filtre (la valeur typique est 2).

Un sous-échantillon a trois objectifs principaux:

• Diminution de la dimension spatiale ou sous-échantillonnage. Ceci est fait pour réduire le nombre de paramètres.
• La croissance de la zone de sensibilité. En raison du sous-échantillon de neurones dans les couches suivantes, davantage d'étapes du signal d'entrée sont accumulées
• Invariance translationnelle à de petites hétérogénéités dans la position des motifs dans le signal d'entrée. En calculant les statistiques d'agrégation de petits voisinages du signal d'entrée, un sous-échantillon peut ignorer les petits déplacements spatiaux qu'il contient.

Couches épaisses

Les couches convolutives et les couches de sous-échantillons ont le même objectif - générer des attributs d'image. La dernière étape consiste à classer l'image d'entrée en fonction des caractéristiques détectées. Chez CNN, des couches denses au sommet du réseau le font. Cette partie du réseau est appelée classification . Il peut contenir plusieurs couches les unes sur les autres avec une connectivité complète, mais se termine généralement par une couche de classe softmax activée par une fonction d'activation logistique multi-variable, dans laquelle le nombre de blocs est égal au nombre de classes. À la sortie de cette couche se trouve la distribution de probabilité par classe pour l'objet d'entrée. Maintenant, l'image peut être classée en choisissant la classe la plus probable.