"Mais nous faisons des fusées!"

Dans un article précédent, j'ai vérifié s'il était possible d'ajuster automatiquement un contrôleur flou en utilisant des «méthodes standard» d'optimisation. Cela s'est avéré possible et le résultat du réglage automatique est tout à fait satisfaisant. Du moins pour la fusée dont le modèle a été utilisé.

Pour les objets de contrôle non fixes où les paramètres d'objet varient sur de larges plages, un contrôleur flou peut ne pas fournir une qualité de contrôle suffisante dans toutes les plages de fonctionnement. Dans ce cas, il est nécessaire d'utiliser un contrôleur flou avec «tuning multicanal».

Vérifions s'il est possible de configurer un tel régulateur en utilisant des méthodes d'optimisation standard.
Considérez la synthèse d'un contrôleur flou avec réglage multicanal pour stabiliser un missile balistique en angle de tangage. Comme demandé dans les commentaires, le missile sera FAU-2. Nous utilisons un exemple du même livre de V. Gostev. "Régulateurs flous dans les systèmes de contrôle automatique."

Tous les termes utilisés dans ce texte sont tirés de ce livre et peuvent ne pas correspondre à la terminologie stricte de la théorie de la commande automatique.

Énoncé du problème

Un missile balistique qui utilise un grand nombre de systèmes de contrôle locaux est un objet de contrôle essentiellement non stationnaire. Les fonctions de transfert, qui décrivent la fusée comme un objet de contrôle, diffèrent des fonctions de transfert des aéronefs ailés en ce sens qu'elles ont des liaisons instables, de sorte que le mouvement d'une fusée non contrôlée le long d'un trajet programmé serait instable.

Ci-dessous, nous considérons le système de stabilisation d'un missile balistique en angle de tangage (canal de mouvement longitudinal). Le système comprend les éléments fonctionnels nécessaires suivants:
un élément de comparaison (un gyroscope libre avec un capteur potentiométrique caractérisé par des coefficients Kp);
amplificateur de puissance Ku et appareil à gouverner hydraulique.

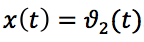
Prendre l'angle de tangage comme coordonnée de sortie de la fusée , pour la coordonnée d'entrée - angle de braquage , nous définissons la fonction de transfert sous la forme:


(L'appareil à gouverner analogique et la fusée sont inclus dans l'objet de commande) Les paramètres de la fonction de transfert seront des polynômes dépendant du temps. Mathématiquement, ils peuvent être déterminés par des polynômes:











La tâche suppose que l'heure de début du vol est de 6 secondes. Les valeurs polynomiales sont acceptées avec un décalage de 6 secondes.
Le modèle mathématique de la liaison oscillatoire non stationnaire est décrit par l'équation différentielle:



Le modèle mathématique d'un lien de forçage instationnaire est décrit par l'équation différentielle:



L'erreur de mésappariement à l'entrée du contrôleur flou est la différence entre l'ensemble et l'angle de tangage requis.

Le schéma structurel du modèle est illustré à la figure 1. Afin de comprendre le principe de formation du modèle, les lignes de communication indiquent les variables X1, X et leurs dérivées ( X1 '', X1 '', X ' ) selon les équations des liens. Le rectangle vert indique la partie du circuit modèle correspondant à la liaison oscillante, et la jaune est la liaison forcée.

Les paramètres a (t), b (t), c (t), r (t) sont fixés sous forme de facteurs d'amplification, en blocs de type «amplificateur». Paramètre est défini dans le gain de la liaison d'intégration.


Figure 1. Diagramme structurel du modèle.

Chemin du logiciel, étant donné l'angle de tangage u (t) = 1 + 0,5 sin (πt / 30).
Des graphiques des changements des paramètres des fusées pendant le vol sont présentés à la figure 2.
La valeur de t = 6 est prise comme début du vol; dans la fonction polynomiale, la valeur (temps + 6) est utilisée pour calculer les paramètres, où le temps est le temps de simulation actuel.


Figure 2. Graphiques des changements dans les paramètres de la fusée.

Contrôleur à logique floue

En tant que contrôleur basé sur une logique floue, nous utilisons le contrôleur illustré à la figure 3. Un décalage entre l'angle de tangage donné et l'angle de tangage réel du missile est appliqué à l'entrée.

Le retard de bloc par étape de quantification fournit une discrétisation de la conversion d'un signal continu en un signal discret avec un pas d'échantillonnage de 0,01 s.

En utilisant deux retards supplémentaires, les écarts de dérivée première et seconde sont calculés par les méthodes de différence sur l'étape de discrétisation.

Les unités de phasage calculent les valeurs des termes pour l'écart, le taux de changement et l'accélération. (Pour plus d'informations, voir le texte précédent ). A la sortie de chaque bloc de phasage, on obtient un vecteur de termes pour les variables linguistiques. (voir tableau 1)

Variable linguistique	Termes
Déviation	En savoir plus Norm Moins
Taux de changement	Grandit Ne change pas Tombe
Changement plus rapide	Est en augmentation Constante Diminue

Les blocs du démultiplexeur analysent les vecteurs en termes distincts, qui sont transmis aux blocs de traitement logique selon les règles d'inférence floue.
Le résultat de l'inférence floue a également trois variables linguistiques: «réduire», «ne pas changer», «augmenter». Les règles d'inférence suivantes sont écrites sous la forme d'un diagramme.

• Si More and Growing et le taux de croissance augmentent => diminuer .
• Si la norme , et ne change pas et est constante => on ne change pas .
• Si Less et Falls et le taux de chute augmentent => augmenter .

Figure 3. Schéma d'un régulateur basé sur une logique floue.

Dans la dénazification, des fonctions triangulaires avec une base commune sont utilisées comme fonction d'appartenance (voir Fig.4)

Figure 4. Fonctions de phasage triangulaire avec une base commune.

On suppose que les fonctions sont symétriques par rapport à 0, dans ce cas, pour décrire trois fonctions triangulaires, une valeur de Max suffit. Pour ceux illustrés sur la figure, Max = 30.

Les mêmes fonctions d'appartenance sont utilisées pour la sortie.

Pour une définition complète du régulateur, il est nécessaire de fixer les valeurs maximales pour les blocs de variable de phase des variables:

- deltaMax - écart maximal;
- divMax - la dérivée maximale de l'écart;
- div2Max - dérivée seconde maximale de l'écart;
- uMax - action de contrôle maximale.

Optimisation complète des processus

L'action de contrôle maximale est prise égale à uMax - 70.
Il nous reste donc à choisir 3 paramètres pour la fonction de déphasage.
Dans ce problème, l'inadéquation est alimentée par un pas au moment zéro du temps du modèle, u (t) = 1 + 0,5.sin (πt / 30).

La trajectoire programmée, l'angle de tangage donné u (t) = 1 + 0,5sin (πt / 30), provoque un effet pas à pas à la première seconde du processus de transition, comme il s'est avéré lors des expériences avec la tâche précédente, les contrôleurs réglés sur un processus de contrôle en douceur, avec une action pas à pas, peuvent ne fournissent pas la qualité requise du processus de transition.

Par conséquent, pour l'optimisation, nous formons 3 critères:

1. Temps transitoire - nous devons arriver à un chemin de programme donné le plus rapidement possible.
2. Écart type.
3. Nombre de commutations - dans des expériences avec la tâche précédente, nous avons eu l'option quand il y avait des oscillations à haute fréquence de l'action de commande à la sortie dans le système de commande.

Le schéma général du bloc d'optimisation est illustré à la figure 5.

Figure 5. Schéma du bloc d'optimisation.

Paramètres d'entrée du bloc d'optimisation:

- écart par rapport à l'angle de tangage donné.
- impact réglementaire.

Pour calculer le temps transitoire, un commutateur est utilisé dans lequel le temps du modèle actuel est appliqué à l'une des entrées. Après le bloc, il y a un retard pour la période de quantification, la valeur du retard est transmise à la deuxième entrée.

En tant que commutateur, un module de déviation est utilisé. Si le module d'écart est supérieur à la valeur de commutation définie (0,02), alors l'heure actuelle est sortie au bloc; si le module est inférieur à la valeur définie, le temps stocké lorsque l'écart était supérieur est transmis à la sortie. Si l'écart dépasse encore la limite, nous obtenons à nouveau le temps. Ainsi, à la sortie, nous avons toujours la dernière fois où l'écart a dépassé la valeur définie.
En tant qu'unité de commutation, le signe de l'action de commande passe de + à -. Pour calculer le nombre de commutations, nous utilisons le bloc "impulsion le long du front" qui, lorsque l'entrée passe de 0 à 1, donne une impulsion de durée dans l'étape d'intégration, les impulsions sont calculées par l'intégrateur. À la sortie du bloc - le nombre de commutations.

- Le bloc d'optimisation sélectionne les valeurs des paramètres à optimiser de manière à minimiser les trois paramètres:
- deltaMax - écart maximal;
- divMax - la dérivée maximale de l'écart;
- div2Max - la dérivée seconde maximale de l'écart.

Le résultat est l'optimisation du processus de transition complet.

Après avoir commencé le processus d'optimisation, nous avons obtenu les paramètres optimaux suivants pour le contrôleur flou:

- deltaMax = 0,185 - écart maximal;
- divMax = 0,278 - la dérivée maximale de l'écart;
- div2Max = 1,291 - la dérivée seconde maximale de l'écart.

Les résultats du processus optimisé sont présentés dans la figure 6.

Figure 6a. Le processus de transition.

Figure 6b. Options de contrôle.

On peut voir que l'optimisation, dans l'ensemble, a été un succès, mais des écarts par rapport à l'angle de tangage donné existent presque tout au long du processus. Le graphique de l'écart agrandi montre que les écarts après l'optimisation et l'achèvement du processus de transition se situent dans la plage de 0,015 à 0,02. (voir fig.7)

Figure 7. Écart dans le processus de contrôle.

Optimisation par sections de vol.

Essayons d'améliorer le processus en sélectionnant les paramètres du contrôleur flou pour différentes sections du vol de fusée.

La première section est le temps entre le début et la sortie sur un chemin donné. Sur la base du graphique de l'écart, le processus de transition associé à l'effet pas à pas initial se termine quelque part à 20 secondes. (voir fig.7). Dans cette section, l'optimisation temporelle du processus de transition se produit.

Réglez l'heure de fin du calcul sur 20 secondes. Et nous effectuerons l'optimisation, en supprimant l'écart-type des critères. Nous allons optimiser au moment du processus de transition et du nombre de commutations. Le schéma fonctionnel d'optimisation est illustré à la figure 8.


Figure 8. Schéma d'optimisation dans la première phase de vol.

L'optimisation automatique pour la première phase du vol jusqu'à 20 secondes a produit les paramètres suivants pour la régulation floue:

- deltaMax = 0,056– écart maximum;
- divMax = 0,0968 - la dérivée maximale de l'écart;
- div2Max = 0,987 - la dérivée seconde maximale de l'écart.

Le processus de transition après l'optimisation est illustré à la figure 9.

Les écarts à plus grande échelle sont illustrés à la figure 10.

Figure 9a. Le processus de transition.

Figure 9b. Options de contrôle.

Figure 10. Écart à plus grande échelle de la première étape du vol.

Les graphiques montrent que le dépassement a diminué et que l'écart après la fin du processus de transition est devenu inférieur à 0,005.

Pour l'optimisation dans la section de vol suivante, nous effectuerons la simulation avec l'état enregistré obtenu dans la première section.

La simulation a lieu de 20 à 40 secondes de vol de missile balistique, l'optimisation se produit tout au long du processus.

Puisque nous avons terminé le processus de transition au début de la deuxième section, nous n'effectuons l'optimisation que par l'écart et le nombre de commutateurs. Le schéma fonctionnel d'optimisation est illustré à la figure 11.


Figure 11. Schéma d'optimisation pour la deuxième section de vol.

L'optimisation automatique pour la deuxième phase du vol de 20 à 40 secondes a produit les paramètres suivants pour la régulation floue:

- deltaMax = 0,056– écart maximum;
- divMax = 0,0974 - la dérivée maximale de l'écart;
- div2Max = 0,980 - la dérivée seconde maximale de l'écart.

Avec les paramètres donnés, l'écart de l'angle de tangage par rapport à celui donné diminue sur toute la seconde section de temps du vol. Mais si nous utilisons les paramètres obtenus par optimisation dans la deuxième partie du vol pour contrôler jusqu'à 66 secondes, alors on peut voir que la précision commence à diminuer et l'écart commence à augmenter après 40 secondes (voir Fig.12).


Figure 12. Processus de contrôle des missiles balistiques avec des paramètres optimisés pour un vol de 20 à 40 secondes.

Répétez l'optimisation pour la troisième étape du vol. Enregistrez les résultats pendant 40 secondes.

Nous les utilisons pour démarrer et optimiser dans une section de 40 à 66 secondes.

L'optimisation automatique pour la dernière section de vol de 40 à 66 secondes a produit les paramètres suivants pour la régulation floue:

- deltaMax = 0,0146– écart maximum;
- divMax = 0,0157– la dérivée maximale de l'écart;
- div2Max = 0,555 - la dérivée seconde maximale de l'écart.

Le graphique du processus de contrôle dans la dernière section du vol du missile balistique après optimisation est illustré à la figure 13.

Figure 13. Processus de contrôle des missiles balistiques dans la dernière étape du vol.

La figure 13 montre qu'avec les nouveaux paramètres, l'écart dans l'intervalle de temps de vol de 40 à 66 secondes n'augmente pas, contrairement aux paramètres optimisés pour le deuxième segment de vol (voir figure 12).

Ainsi, nous avons obtenu les paramètres du contrôleur flou pour trois sections du vol. Créons un commutateur de mode qui changera les paramètres du contrôleur pendant le vol. Le circuit du commutateur de mode est illustré à la figure 14.


Figure 14. Commutateur de mode du contrôleur de missile balistique flou.

Les modes de commutation auront lieu dans le temps, dans la partie supérieure un simple circuit logique compare l'heure actuelle du modèle avec les points de commutation. En conséquence, un vecteur de commande de trois valeurs est formé dans le multiplexeur. Dans ce vecteur, la valeur 1 est à la position de l'intervalle de temps actuel.

Les paramètres du contrôleur flou calculés précédemment par les méthodes d'optimisation sont regroupés en vecteurs de trois valeurs.

A l'aide d'un bloc d'échantillonnage de trois valeurs, une est sélectionnée qui correspond à 1 dans le vecteur de contrôle Ainsi, lorsque le temps change, les paramètres transférés au contrôleur flou changent en fonction de la section de vol en cours.

Pour plus de clarté, les valeurs transmises sur la ligne de communication sont affichées dans le diagramme. Le chiffre correspond à la dernière section d'un vol de missile balistique. Le temps est supérieur à 40 secondes. Le vecteur de contrôle (0,0,1) dans le contrôleur est le dernier paramètre de l'ensemble.

Le résultat de la simulation du contrôle de l'angle de tangage de la fusée avec la commutation des paramètres du régulateur est illustré à la figure 15.

Figure 15a. Le processus de transition.

Figure 15b. Options de contrôle.

Conclusions:
Un contrôleur basé sur une logique floue peut être configuré par la méthode d'optimisation pour fonctionner en mode de commutation de paramètres.

L'écart lors du travail avec des paramètres variables dans l'exemple donné a diminué de 3 à 5 fois par rapport au fonctionnement du contrôleur avec des paramètres constants.

Les archives des projets d'étude indépendante peuvent être téléchargées ici ...