L'essence générale des tri par insertion est la suivante:
- Itère les éléments de la partie non triée du tableau.
- Chaque élément est inséré dans la partie triée du tableau à l'endroit où il devrait être.
C'est, en principe, tout ce que vous devez savoir sur le tri par encarts. Autrement dit, les tris par insertion divisent toujours le tableau en 2 parties - triées et non triées. Tout élément est récupéré de la partie non triée. Puisque l'autre partie du tableau est triée, vous pouvez rapidement trouver votre place dans ce tableau pour cet élément extrait. L'élément est inséré si nécessaire, à la suite de quoi la partie triée du tableau augmente et la partie non triée diminue. C’est tout. Toutes sortes d'inserts fonctionnent selon ce principe.
Le point le plus faible de cette approche est l'insertion d'un élément dans la partie triée du tableau. En fait, ce n'est pas facile et quelles astuces vous n'avez pas à suivre pour terminer cette étape.
Tri par insertion simple

Nous parcourons le tableau de gauche à droite et traitons chaque élément tour à tour. À gauche de l'élément suivant, nous augmentons la partie triée du tableau, à droite, au fur et à mesure que le processus progresse, la partie non triée s'évapore lentement. Dans la partie triée du tableau, le point d'insertion de l'élément suivant est recherché. L'élément lui-même est envoyé au tampon, à la suite duquel une cellule vide apparaît dans le tableau - cela vous permet de déplacer les éléments et de libérer le point d'insertion.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
En utilisant des insertions simples à titre d'exemple, le principal avantage de la plupart (mais pas de toutes!) Le tri par insertions semble démonstratif, à savoir un traitement très rapide de tableaux presque ordonnés:

Dans ce scénario, même l'implémentation la plus primitive des insertions de tri est susceptible de dépasser l'algorithme super-optimisé pour un tri rapide, y compris sur les grands tableaux.
Ceci est facilité par l'idée principale de cette classe - le transfert d'éléments de la partie non triée du tableau vers la partie triée. À proximité de données de magnitude similaire, le point d'insertion est généralement situé près du bord de la partie triée, ce qui vous permet d'insérer avec le moins de frais généraux.
Il n'y a rien de mieux pour gérer des tableaux presque ordonnés que le tri par insertion. Lorsque vous rencontrez des informations quelque part selon lesquelles la meilleure complexité temporelle du tri par insertions est
O ( n ) , vous faites probablement référence à des situations avec des tableaux presque ordonnés.
Trier par de simples insertions de recherche binaire

Puisque l'endroit à insérer est recherché dans la partie triée du tableau, l'idée d'utiliser une recherche binaire se suggère. Une autre chose est que la recherche du site d'insertion n'est pas critique pour la complexité temporelle de l'algorithme (le principal mangeur de ressources est l'étape d'insertion de l'élément dans la position trouvée elle-même), donc cette optimisation fait peu.
Et dans le cas d'un tableau presque trié, une recherche binaire peut fonctionner encore plus lentement, car elle commence au milieu de la section triée, ce qui, très probablement, sera trop loin du point d'insertion (et il faudra moins d'étapes pour effectuer une recherche normale de la position de l'élément au point d'insertion si les données dans le tableau dans son ensemble ordonné).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
Pour la défense de la recherche binaire, je note qu'il peut dire le dernier mot dans l'efficacité des autres tris par encarts. Grâce à lui, en particulier, des algorithmes tels que le tri bibliothécaire et le tri solitaire vont à la complexité temporelle moyenne
O ( n log n ) . Mais à leur sujet plus tard.
Tri des paires par inserts simples
Modification d'inserts simples, développés dans les laboratoires secrets d'Oracle Corporation. Ce tri fait partie du JDK et fait partie du tri rapide à double pivot. Il est utilisé pour trier les petits tableaux (jusqu'à 47 éléments) et trier les petites zones des grands tableaux.

Pas un mais deux éléments adjacents sont envoyés au tampon à la fois. Tout d'abord, le plus grand élément de la paire est inséré, et immédiatement après, la méthode d'insertion simple est appliquée au plus petit élément de la paire.
Qu'est-ce que ça donne? Économies pour la manipulation d'un petit article d'une paire. Pour lui, la recherche du point d'insertion et l'insertion elle-même ne sont effectuées que sur cette partie triée du tableau, qui n'inclut pas la zone triée utilisée pour traiter un élément plus grand de la paire. Cela devient possible car les éléments plus grands et plus petits sont traités immédiatement l'un après l'autre en un seul passage de la boucle extérieure.
Cela n'affecte pas la complexité temporelle moyenne (elle reste toujours égale à
O ( n 2 )), cependant, les inserts appariés fonctionnent un peu plus vite que les inserts habituels.
J'illustre les algorithmes en Python, mais ici je donne la source originale (modifiée pour plus de lisibilité) en Java:
for (int k = left; ++left <= right; k = ++left) {
Tri des coques

Cet algorithme a une approche très spirituelle pour déterminer quelle partie du tableau est considérée comme triée. Dans les insertions simples, tout est simple: à partir de l'élément courant, tout à gauche est déjà trié, tout à droite n'est pas encore trié. Contrairement aux insertions simples, le tri Shell n'essaie pas de former immédiatement une partie strictement triée du tableau à gauche d'un élément. Il crée une partie
presque triée du tableau à gauche de l'élément et le fait assez rapidement.
Le tri par shell jette l'élément actuel dans le tampon et le compare avec le côté gauche du tableau. S'il trouve des éléments plus gros sur la gauche, il les déplace vers la droite, laissant de la place pour l'insertion. Mais en même temps, il ne prend pas toute la partie gauche, mais seulement un certain groupe d'éléments, où les éléments sont espacés les uns des autres d'une certaine distance. Un tel système vous permet d'insérer rapidement des éléments dans approximativement la zone du réseau où ils doivent être situés.
À chaque itération de la boucle principale, cette distance diminue progressivement et lorsqu'elle devient égale à un, le tri Shell se transforme à ce moment en un tri classique avec des insertions simples, qui ont été données au traitement d'un tableau presque trié. Un tableau de tri presque trié s'insère en convertis entièrement triés rapidement.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
Le tri par peigne selon un principe similaire améliore le tri à bulles, de sorte que la complexité temporelle de l'algorithme avec
O ( n 2 ) passe directement à
O ( n log n ) . Hélas, Shell ne parvient pas à répéter cet exploit - la meilleure complexité temporelle atteint
O ( n log 2 n ) .
Plusieurs habrastati ont été écrits sur le tri de Shell, nous ne serons donc pas surchargés d'informations et continuerons.
Tri des arbres
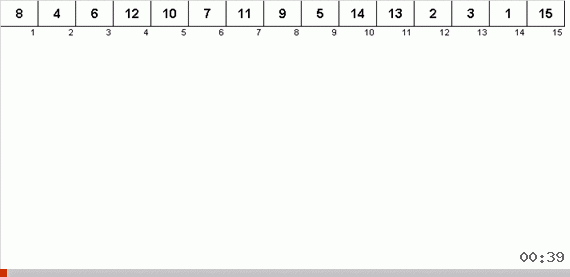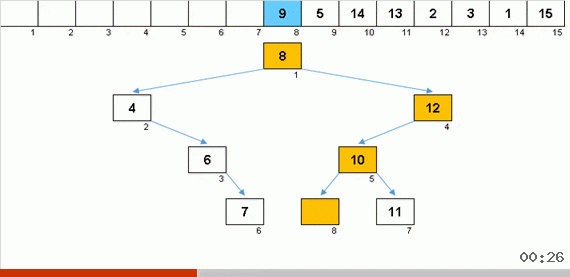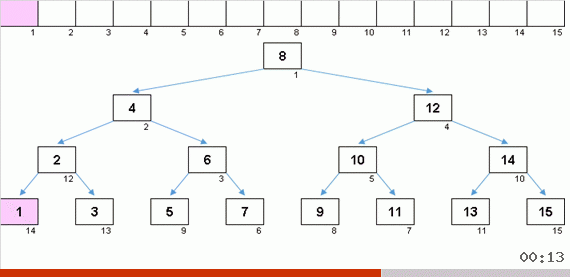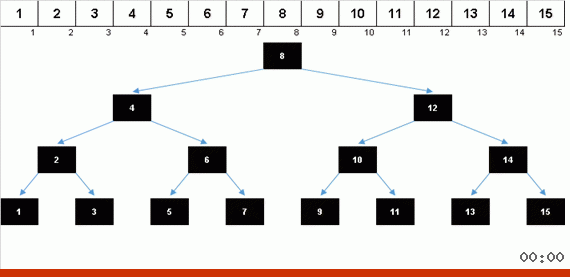
Le tri avec une arborescence en raison de la mémoire supplémentaire résout rapidement le problème de l'ajout d'un autre élément à la partie triée du tableau. De plus, l'arbre binaire agit comme la partie triée du tableau. Un arbre se forme littéralement à la volée lors de l'itération sur des éléments.
L'élément est d'abord comparé avec la racine, puis avec plus de nœuds imbriqués selon le principe: si l'élément est plus petit que le nœud, alors on descend la branche gauche, sinon moins, puis la droite. Un arbre construit par une telle règle peut alors être facilement contourné de manière à passer de nœuds avec des valeurs plus faibles à des nœuds avec des valeurs plus grandes (et ainsi obtenir tous les éléments dans un ordre croissant).
Le problème principal du tri par insertions (le coût de l'insertion d'un élément à sa place dans la partie triée du tableau) est résolu ici, la construction se déroule assez rapidement. Dans tous les cas, pour libérer le point d'insertion, il n'est pas nécessaire de déplacer lentement les caravanes d'éléments comme dans les algorithmes précédents. Il semblerait que le voici, le meilleur des trieurs. Mais il y a un problème.
Lorsque vous obtenez un bel arbre de Noël symétrique (le soi-disant arbre parfaitement équilibré) comme dans l'animation trois paragraphes ci-dessus, l'insertion se produit rapidement, car l'arbre dans ce cas a les niveaux d'imbrication les plus bas possibles. Mais une structure équilibrée (ou au moins proche de cela) à partir d'un tableau aléatoire est rarement obtenue. Et l'arbre, très probablement, sera imparfait et déséquilibré - avec des distorsions, un horizon jonché et un nombre excessif de niveaux.
Un tableau aléatoire avec des valeurs de 1 à 10. Les éléments dans cet ordre génèrent un arbre binaire déséquilibré: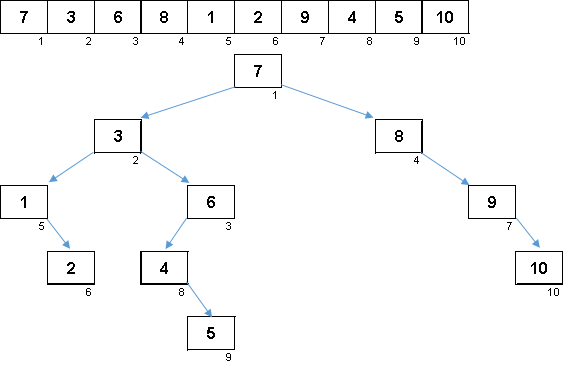
Un arbre ne suffit pas à construire, il doit encore être contourné. Plus le déséquilibre est important, plus l'algorithme de traversée de l'arbre glissera fort. Ici, comme le disent les étoiles, un tableau aléatoire peut générer à la fois un vilain accroc (ce qui est plus probable) et une fractale en forme d'arbre.
Les valeurs des éléments sont les mêmes, mais l'ordre est différent. Un arbre binaire équilibré est généré: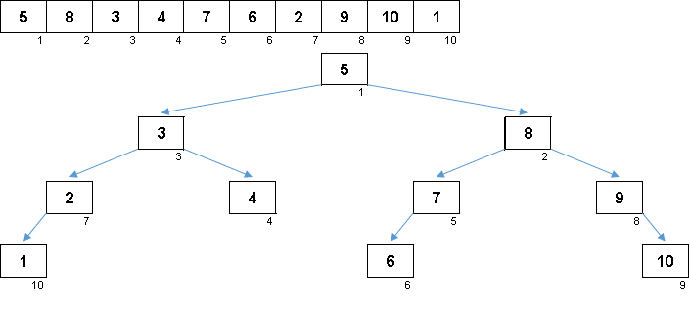
 Sur la belle sakura
Sur la belle sakura
Pas assez de pétale:
Un arbre binaire de dizaines.Le problème des arbres déséquilibrés est résolu par le tri par inversion, qui utilise un type spécial d'arbre de recherche binaire - arbre splay. Il s'agit d'un magnifique arbre de transformateur qui, après chaque opération, est reconstruit dans un état équilibré. À ce sujet sera un article séparé. À ce moment-là, je préparerai des implémentations Python pour le tri arborescent et le tri Splay.
Eh bien, eh bien, nous avons brièvement examiné les encarts de tri les plus populaires. Inserts simples, coque et arbre binaire que nous connaissons tous à l'école. Considérons maintenant d'autres représentants de cette classe, moins connus.
Wiki / Wiki -
Insertion , Shell / Shell , Arbre / ArbreArticles de série:
Qui utilise AlgoLab - Je recommande de mettre à jour le fichier. J'ai ajouté des insertions de recherche binaires simples et des insertions appariées à cette application. Il a également complètement réécrit la visualisation pour Shell (dans la version précédente, il n'y avait rien à comprendre) et a ajouté une surbrillance à la branche parent lors de l'insertion d'un élément dans l'arbre binaire.