Réseaux de neurones, principes fondamentaux de fonctionnement, diversité et topologie

Les réseaux de neurones ont révolutionné le domaine de la reconnaissance des formes, mais en raison de l'interprétabilité non évidente du principe de fonctionnement, ils ne sont pas utilisés dans des domaines tels que la médecine et l'évaluation des risques. Il nécessite une représentation visuelle du réseau, ce qui en fera non pas une boîte noire, mais au moins «translucide». Cristopher Olah, dans Neural Networks, Manifolds, and Topology, a démontré les principes de fonctionnement des réseaux de neurones et les a connectés à la théorie mathématique de la topologie et de la diversité, qui a servi de base à cet article. Pour démontrer le fonctionnement d'un réseau de neurones, des réseaux de neurones profonds de faible dimension sont utilisés.

Comprendre le comportement des réseaux de neurones profonds n'est généralement pas une tâche triviale. Il est plus facile d'explorer des réseaux de neurones profonds de faible dimension - des réseaux dans lesquels il n'y a que quelques neurones dans chaque couche. Pour les réseaux de faible dimension, vous pouvez créer des visualisations pour comprendre le comportement et la formation de ces réseaux. Cette perspective fournira une compréhension plus approfondie du comportement des réseaux de neurones et observera la connexion qui combine les réseaux de neurones avec un domaine mathématique appelé topologie.

Un certain nombre de choses intéressantes en découlent, notamment les limites inférieures fondamentales de la complexité d'un réseau neuronal capable de classer certains ensembles de données.

Considérons le principe du réseau en utilisant un exemple

Commençons par un simple ensemble de données - deux courbes sur un plan. La tâche réseau apprendra à classer les points appartenant aux courbes.



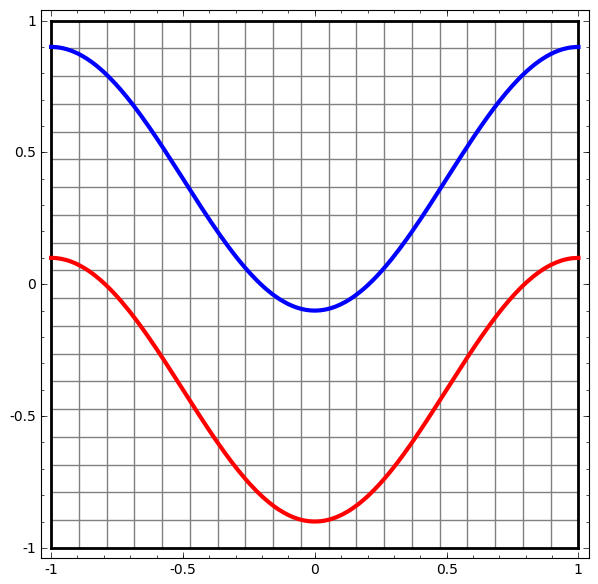
Une façon évidente de visualiser le comportement d'un réseau de neurones, pour voir comment l'algorithme classe tous les objets possibles (dans notre exemple, les points) d'un ensemble de données.

Commençons par la classe la plus simple de réseau neuronal, avec une couche d'entrée et de sortie. Un tel réseau essaie de séparer deux classes de données en les divisant par une ligne.



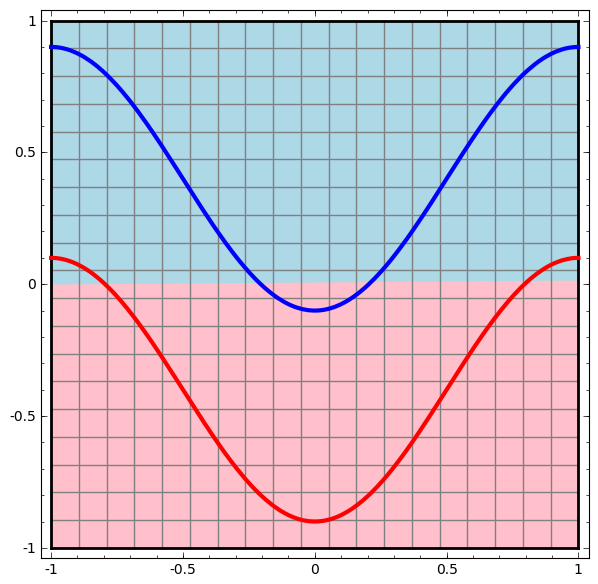
Un tel réseau n'est pas utilisé dans la pratique. Les réseaux de neurones modernes ont généralement plusieurs couches entre leur entrée et leur sortie, appelées couches «cachées».

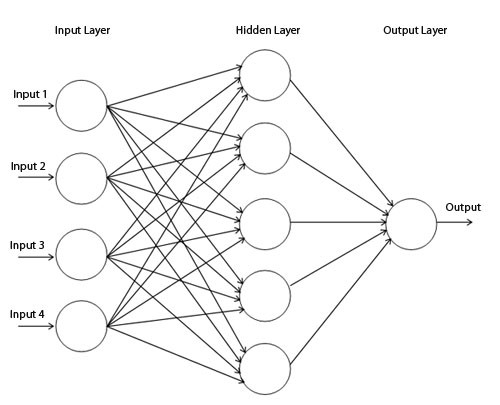
Diagramme de réseau simple

Nous visualisons le comportement de ce réseau, en observant ce qu'il fait avec différents points de son domaine. Un réseau à couche cachée sépare les données d'une courbe plus complexe qu'une ligne.



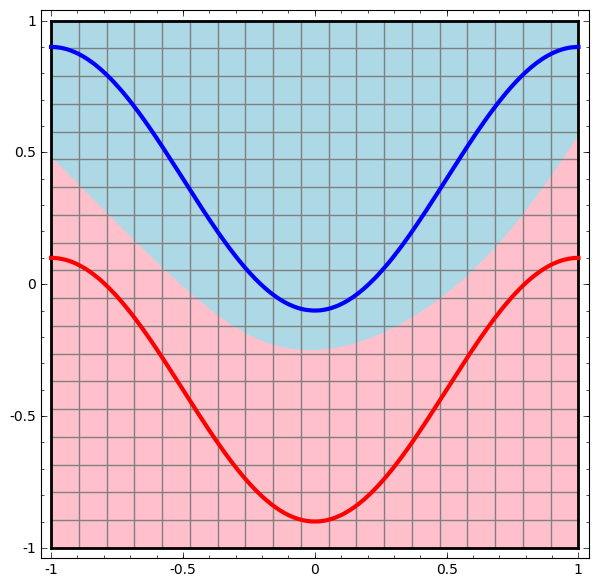
Avec chaque couche, le réseau transforme les données, créant une nouvelle vue. Nous pouvons voir les données dans chacune de ces vues et comment le réseau avec une couche cachée les classe. Lorsque l'algorithme atteint la présentation finale, le réseau neuronal tracera une ligne à travers les données (ou dans des dimensions supérieures - un hyperplan).

Dans la visualisation précédente, les données d'une vue brute sont prises en compte. Vous pouvez l'imaginer en regardant la couche d'entrée. Maintenant, considérez-le après sa conversion en première couche. Vous pouvez l'imaginer en regardant la couche cachée.
Chaque mesure correspond à l'activation d'un neurone dans la couche.



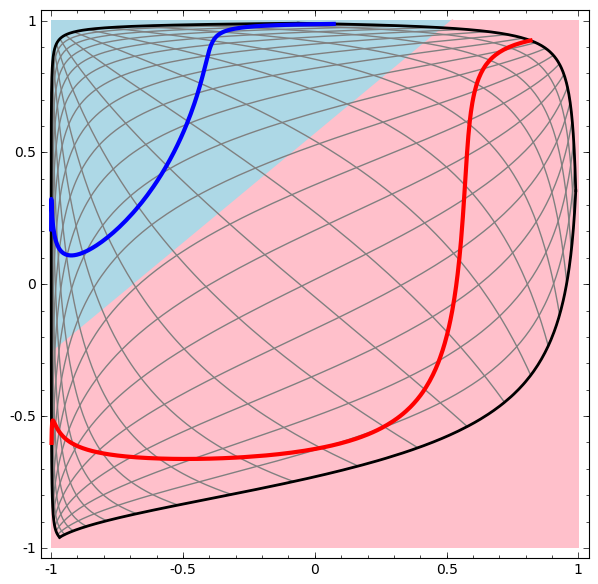
La couche cachée est entraînée sur la vue afin que les données soient linéairement séparables.

Rendu de calque continu

Dans l'approche décrite dans la section précédente, nous apprenons à comprendre les réseaux en regardant la présentation correspondant à chaque couche. Cela nous donne une liste discrète de vues.

La partie non triviale consiste à comprendre comment nous passons de l'un à l'autre. Heureusement, les niveaux de réseau neuronal ont des propriétés qui rendent cela possible.
Il existe de nombreux types de couches différents utilisés dans les réseaux de neurones.

Considérons une couche tanh pour un exemple spécifique. La couche de Tanh-tanh (Wx + b) comprend:

1. La transformation linéaire de la matrice "poids" W
2. Traduction à l'aide du vecteur b
3. Application ponctuelle de tanh.

Nous pouvons représenter cela comme une transformation continue comme suit:



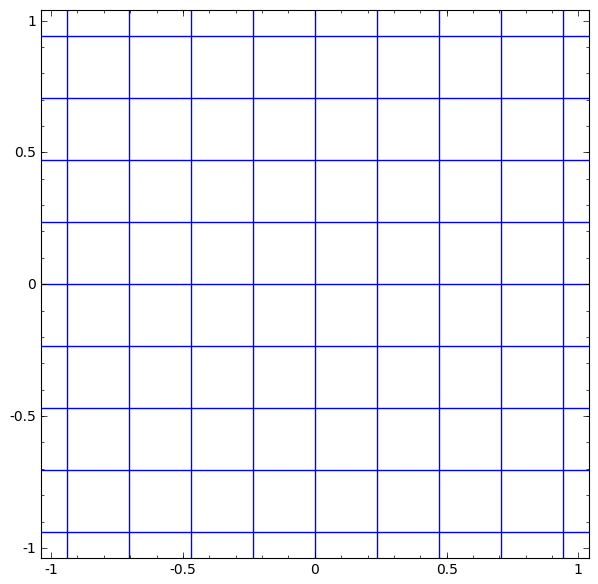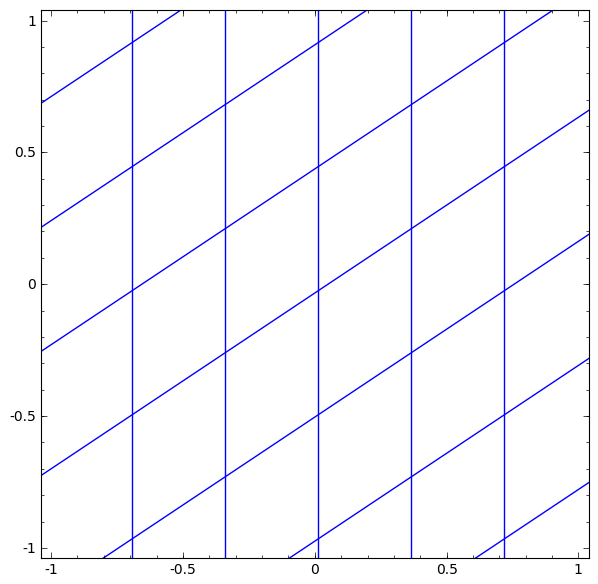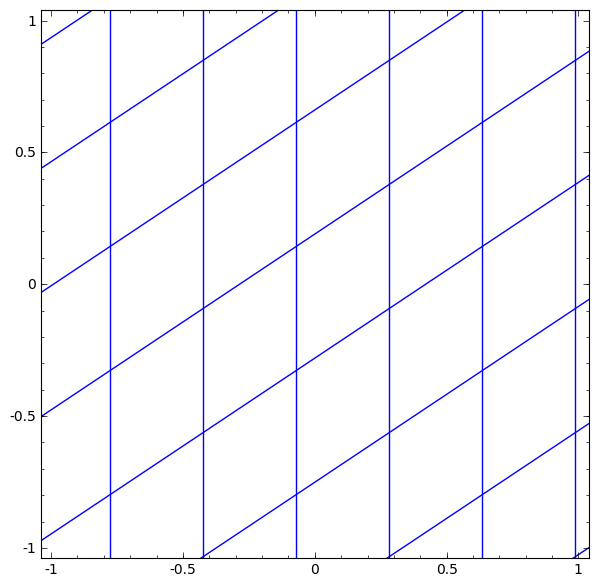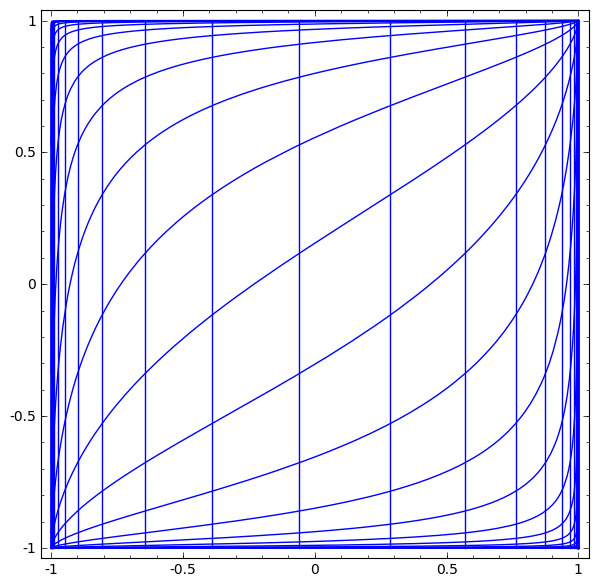
Ce principe de fonctionnement est très similaire à d'autres couches standard consistant en une transformation affine, suivie de l'application ponctuelle d'une fonction d'activation monotone.
Cette méthode peut être utilisée pour comprendre des réseaux plus complexes. Ainsi, le réseau suivant classe deux spirales légèrement emmêlées à l'aide de quatre couches cachées. Au fil du temps, on peut voir que le réseau de neurones passe d'une vue brute à un niveau supérieur que le réseau a étudié pour classer les données. Alors que les spirales sont initialement enchevêtrées, vers la fin, elles sont linéairement séparables.



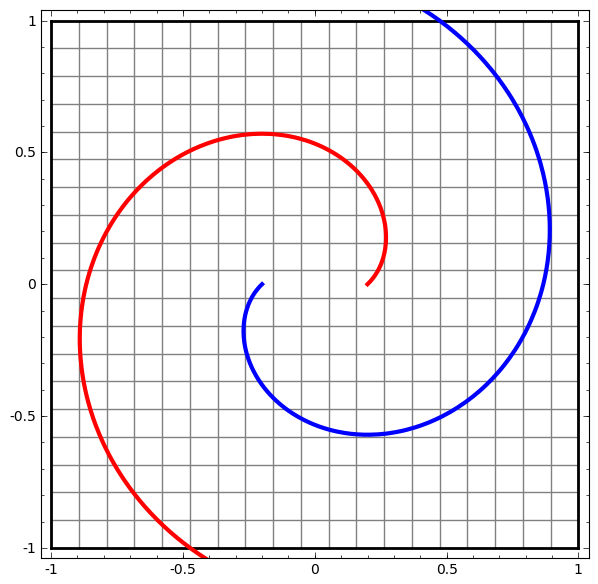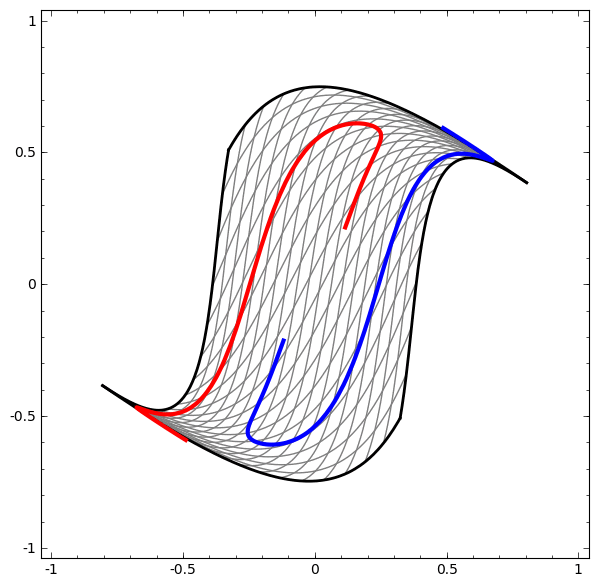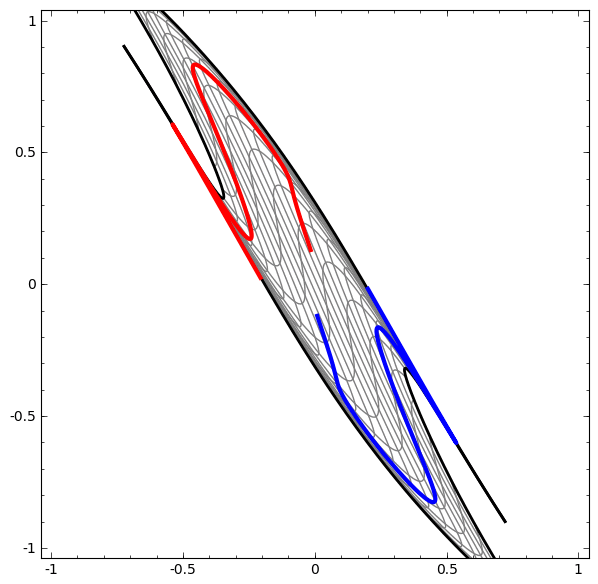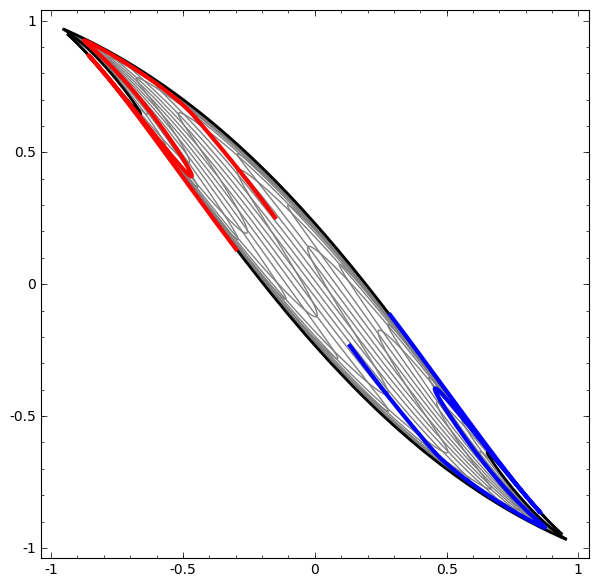
En revanche, le prochain réseau, qui utilise également plusieurs niveaux, mais ne peut pas classer deux spirales, qui sont plus enchevêtrées.



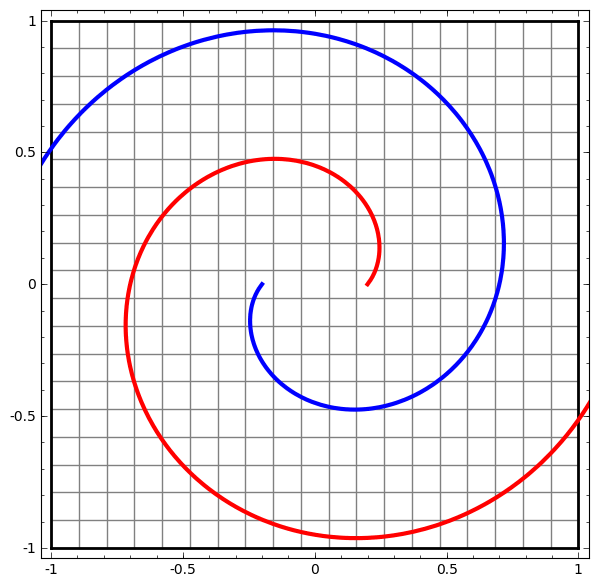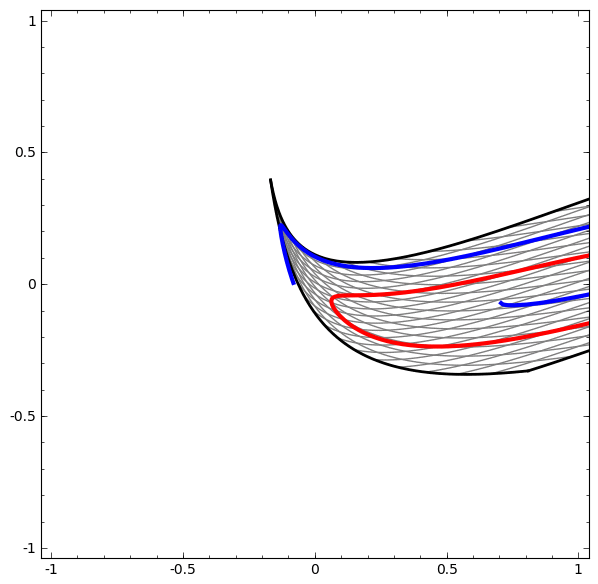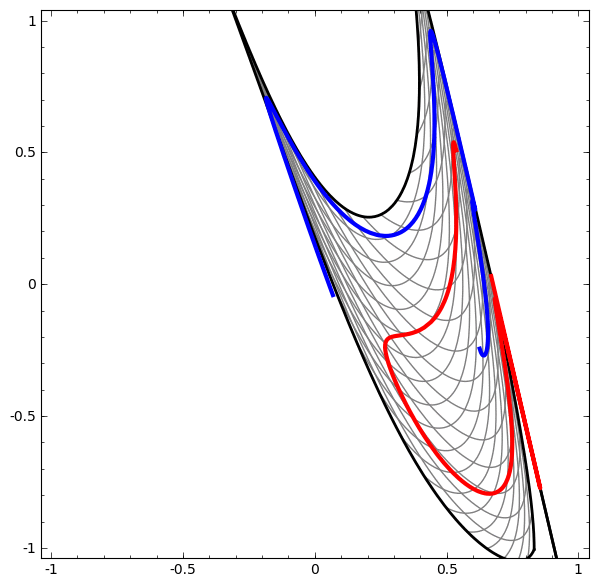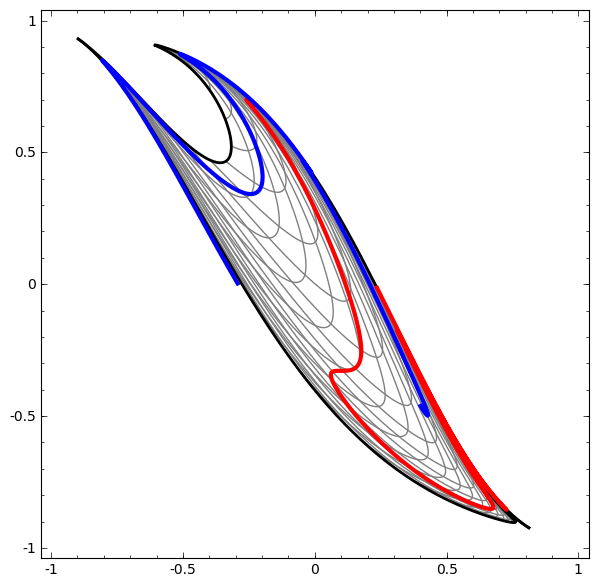
Il convient de noter que ces tâches ont une complexité limitée, car des réseaux de neurones de faible dimension sont utilisés. Si des réseaux plus larges étaient utilisés, la résolution des problèmes était simplifiée.

Couches Tang

Chaque couche étire et comprime l'espace, mais il ne coupe jamais, ne casse pas et ne le plie pas. Intuitivement, nous voyons que les propriétés topologiques sont préservées sur chaque couche.

De telles transformations qui n'affectent pas la topologie sont appelées homomorphismes (Wiki - Ceci est une cartographie du système algébrique A qui préserve les opérations de base et les relations de base). Formellement, ce sont des bijections qui sont des fonctions continues dans les deux sens. Dans un mappage bijectif, chaque élément d'un ensemble correspond exactement à un élément d'un autre ensemble, et un mappage inverse qui a la même propriété est défini.

Le théorème

Les couches à N entrées et N sorties sont des homomorphismes si la matrice de poids W n'est pas dégénérée. (Vous devez faire attention au domaine et à la plage.)

Topologie et classification

Considérons un ensemble de données à deux dimensions avec deux classes A, B⊂R2:

A = {x | d (x, 0) <1/3}

B = {x | 2/3 <d (x, 0) <1}



A rouge, B bleu

Condition: un réseau de neurones ne peut pas classer cet ensemble de données sans 3 couches cachées ou plus, quelle que soit la largeur.

Comme mentionné précédemment, la classification avec une fonction sigmoïde ou une couche softmax équivaut à essayer de trouver l'hyperplan (ou dans ce cas la ligne) qui sépare A et B dans la représentation finale. Avec seulement deux couches masquées, le réseau est topologiquement incapable de partager des données de cette manière et est voué à l'échec dans cet ensemble de données.
Dans la visualisation suivante, nous observons une vue latente pendant que le réseau s'entraîne avec la ligne de classification.



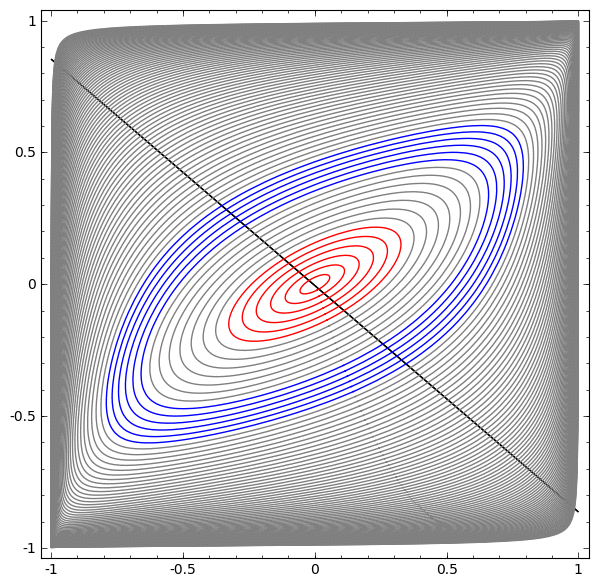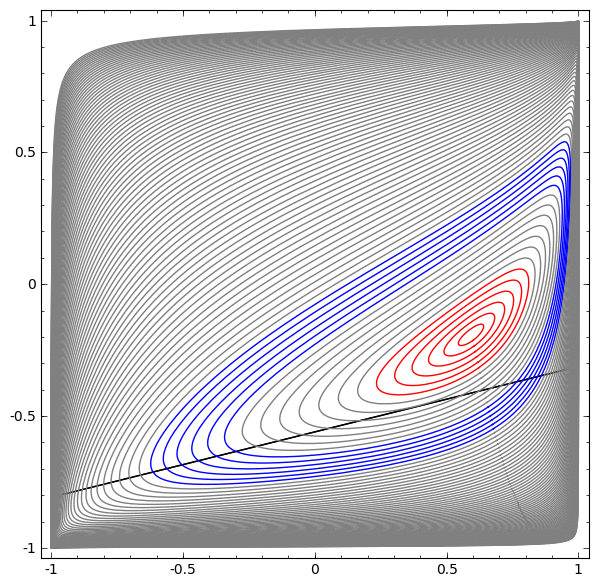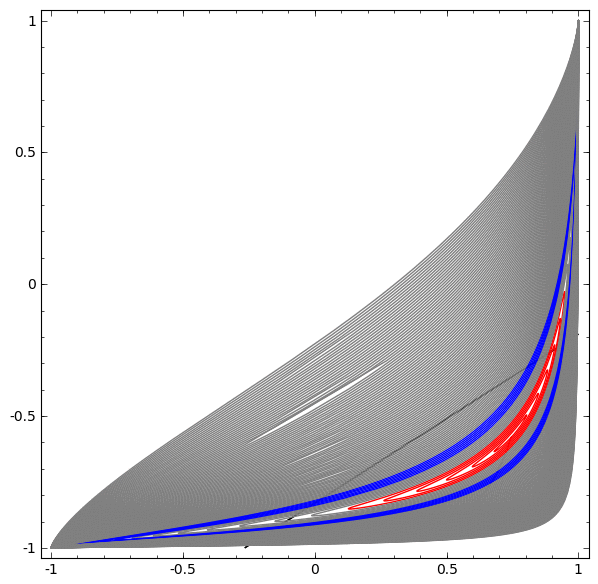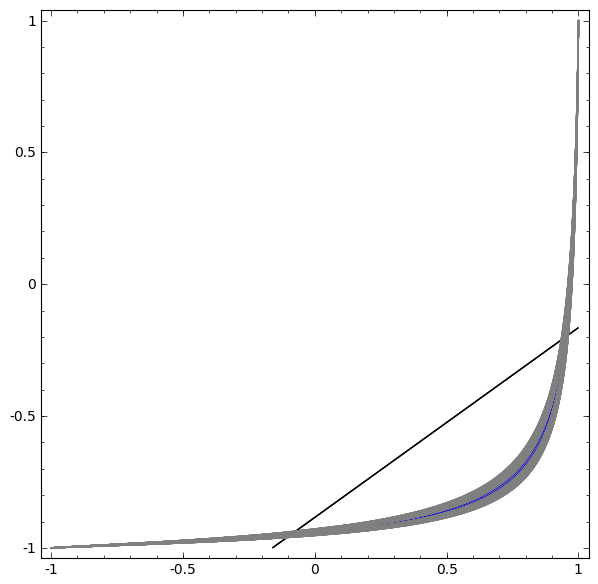
Pour ce réseau de formation, il ne suffit pas d'atteindre un résultat à cent pour cent.
L'algorithme tombe dans un minimum local non productif, mais est capable d'atteindre une précision de classification de ~ 80%.

Dans cet exemple, il n'y avait qu'une seule couche masquée, mais cela n'a pas fonctionné.
Déclaration. Soit chaque couche est un homomorphisme, soit la matrice de poids de la couche a le déterminant 0.


Si nous ajoutons un troisième élément caché, le problème deviendra trivial. Le réseau neuronal reconnaît la représentation suivante:



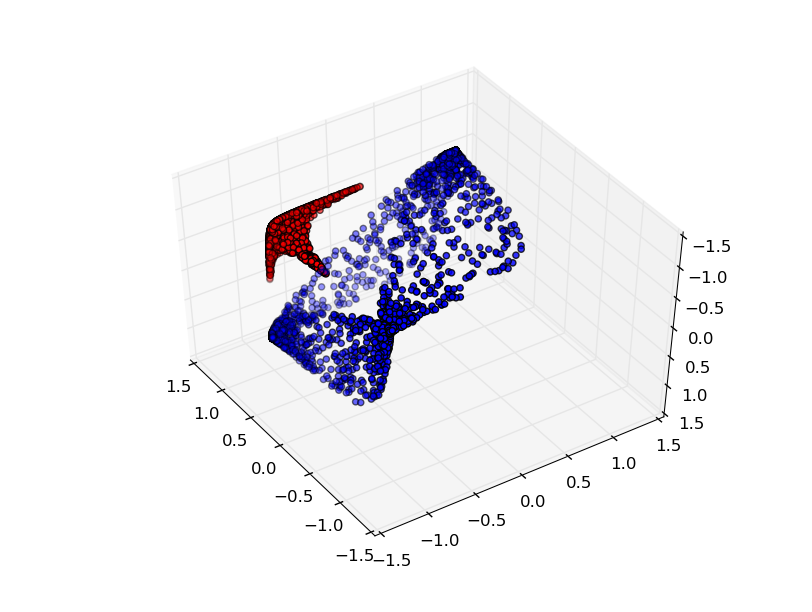
La vue permet de séparer les jeux de données avec un hyperplan.
Pour mieux comprendre ce qui se passe, regardons un ensemble de données encore plus simple, qui est unidimensionnel:



A = [- 1 / 3,1 / 3]
B = [- 1, −2 / 3] ∪ [2 / 3,1]
Sans utiliser une couche de deux ou plusieurs éléments cachés, nous ne pouvons pas classer cet ensemble de données. Mais, si nous utilisons un réseau à deux éléments, nous apprendrons à représenter les données comme une bonne courbe qui nous permet de séparer les classes à l'aide d'une ligne:



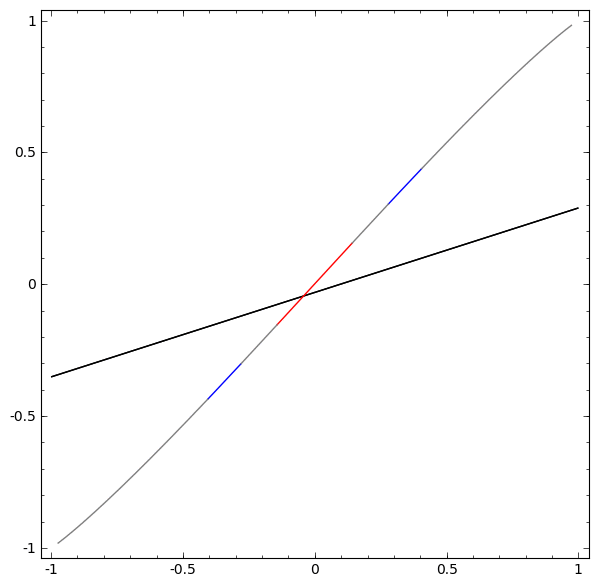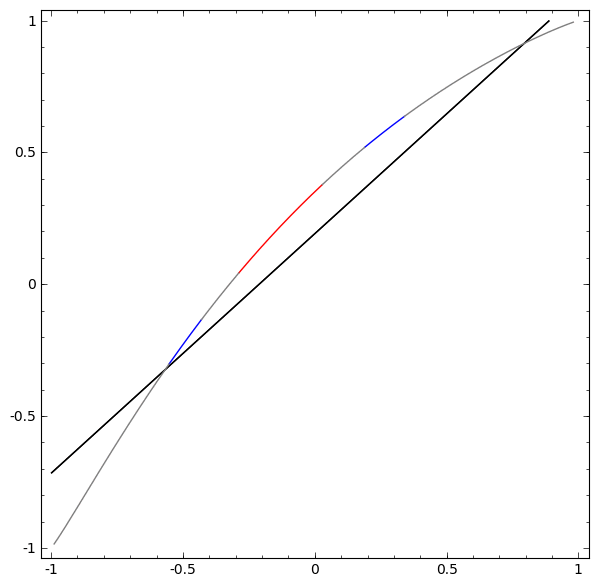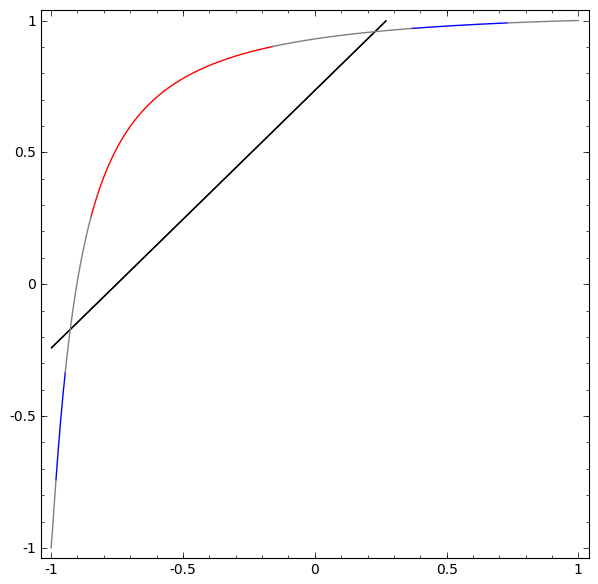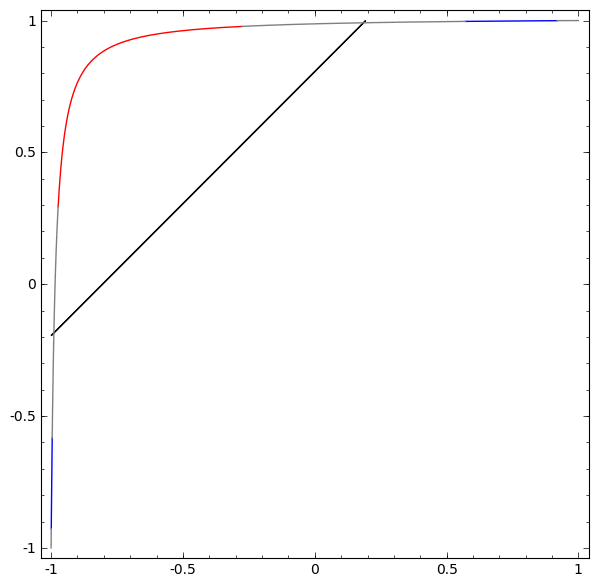
Que se passe-t-il? Un élément caché apprend à tirer lorsque x> -1/2, et l'autre apprend à tirer lorsque x> 1/2. Lorsque le premier est déclenché, mais pas le second, nous savons que nous sommes en A.

Conjecture de variété

Cela s'applique-t-il aux ensembles de données du monde réel, tels que les ensembles d'images? Si vous êtes sérieux au sujet de l'hypothèse de la diversité, je pense que cela compte.

L'hypothèse multidimensionnelle est que les données naturelles forment des variétés de faible dimension dans l'espace d'implantation. Il y a des raisons à la fois théoriques [1] et expérimentales [2] de croire que cela est vrai. Si oui, alors la tâche de l'algorithme de classification est de séparer le faisceau de variétés enchevêtrées.

Dans les exemples précédents, une classe a complètement entouré l'autre. Cependant, il est peu probable que la variété d'images de chiens soit complètement entourée d'une collection d'images de chats. Mais il existe d'autres situations topologiques plus plausibles qui peuvent encore survenir, comme nous le verrons dans la section suivante.

Connexions et homotopies

Un autre jeu de données intéressant est les deux tori connectés A et B.



Comme les précédents ensembles de données que nous avons examinés, cet ensemble de données ne peut pas être divisé sans utiliser n + 1 dimensions, à savoir la quatrième dimension.

Les connexions sont étudiées dans la théorie des nœuds, dans le domaine de la topologie. Parfois, lorsque nous voyons une connexion, il n'est pas immédiatement clair s'il s'agit d'une incohérence (beaucoup de choses qui s'emmêlent mais peuvent être séparées par une déformation continue) ou non.



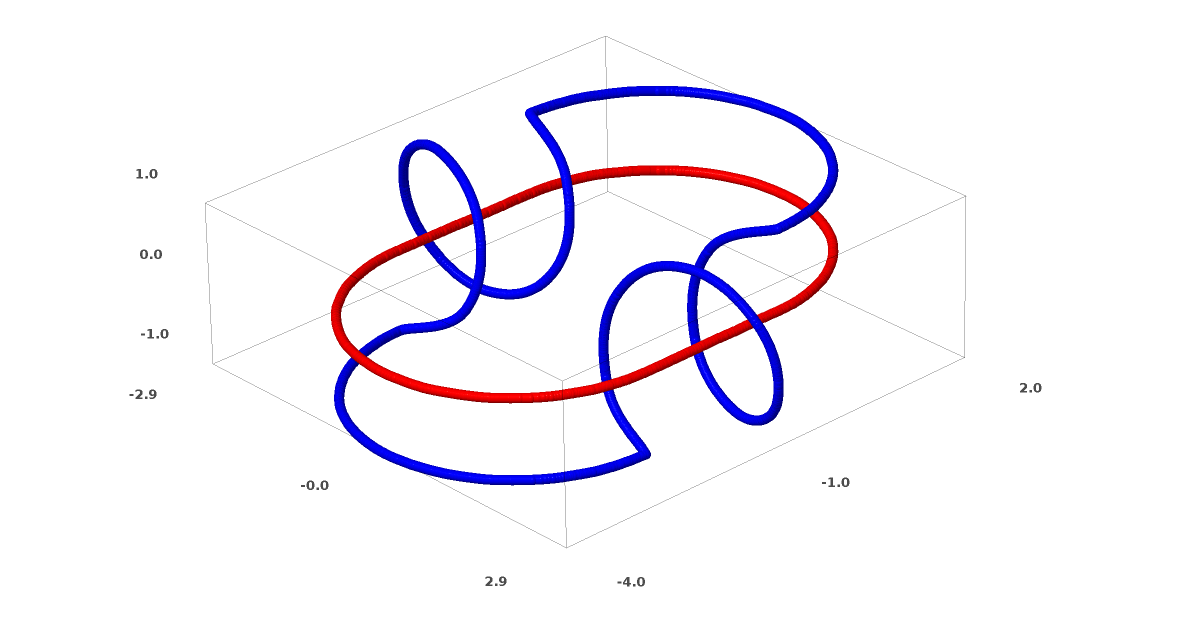
Incohérence relativement simple.

Si un réseau neuronal utilisant des couches avec seulement trois unités peut le classer, alors il est incohérent. (Question: toutes les incohérences peuvent-elles être classées sur le réseau avec seulement trois incohérences, théoriquement?)

Du point de vue de ce nœud, la visualisation continue des représentations créées par un réseau de neurones est une procédure pour dénouer les connexions. En topologie, nous appellerons cette isotopie ambiante entre le lien d'origine et les liens séparés.

Formellement, l'isotopie de l'espace environnant entre les variétés A et B est une fonction continue F: [0,1] × X → Y telle que chaque Ft est un homéomorphisme de X à sa gamme, F0 est une fonction d'identité et F1 mappe A à B. T .e. Ft passe continuellement de la carte A à elle-même, à la carte A à B.

Théorème: il y a une isotopie de l'espace environnant entre l'entrée et la représentation du niveau du réseau si: a) W n'est pas dégénéré, b) nous sommes prêts à transférer des neurones vers la couche cachée et c) il y a plus d'un élément caché.


Jusqu'à présent, il est peu probable que les relations dont nous avons parlé apparaissent dans des données réelles, mais il existe des généralisations d'un niveau supérieur. Il est plausible que de telles fonctionnalités puissent exister dans des données réelles.

Les connexions et les nœuds sont des variétés unidimensionnelles, mais nous avons besoin de 4 dimensions pour que les réseaux puissent tous les démêler. De même, un espace dimensionnel encore plus élevé peut être nécessaire pour pouvoir étendre les variétés à n dimensions. Tous les collecteurs à n dimensions peuvent être étendus en 2n + 2 dimensions. [3]

Sortie facile

Le moyen le plus simple est d'essayer de séparer les collecteurs et d'étirer les pièces aussi emmêlées que possible. Bien que cela ne soit pas proche d'une véritable solution, une telle solution peut atteindre une précision de classification relativement élevée et être un minimum local acceptable.



De tels minima locaux sont absolument inutiles pour essayer de résoudre des problèmes topologiques, mais les problèmes topologiques peuvent fournir une bonne motivation pour étudier ces problèmes.

D'un autre côté, si nous voulons seulement obtenir de bons résultats de classification, l'approche est acceptable. Si un petit morceau d'un collecteur de données est pris sur un autre collecteur, est-ce un problème? Il est probable qu'il sera possible d'obtenir des résultats de classement arbitrairement bons, malgré ce problème.

Des couches améliorées pour manipuler les collecteurs?

Il est difficile d'imaginer que les couches standard avec des transformations affines sont vraiment bonnes pour manipuler les variétés.

Peut-être qu'il est logique d'avoir une couche complètement différente, que nous pouvons utiliser dans la composition avec des couches plus traditionnelles?

L'étude d'un champ vectoriel avec une direction dans laquelle nous voulons déplacer la variété est prometteuse:



Et puis nous déformons l'espace en fonction du champ vectoriel:



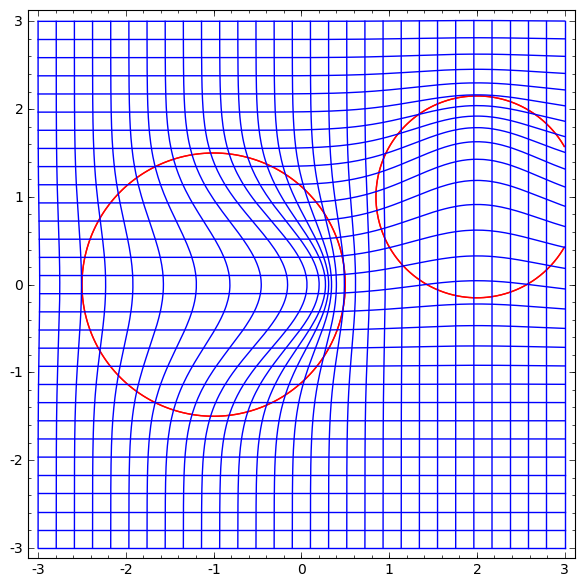
On pourrait étudier le champ vectoriel à des points fixes (il suffit de prendre quelques points fixes de l'ensemble de données de test pour les utiliser comme ancres) et interpoler en quelque sorte.


Où v0 et v1 sont des vecteurs, et f0 (x) et f1 (x) sont des Gaussiens à n dimensions.

Couches K-voisins les plus proches

La séparabilité linéaire peut être un besoin énorme et peut-être déraisonnable pour les réseaux de neurones. Il est naturel d'utiliser la méthode des k plus proches voisins (k-NN). Cependant, le succès du k-NN dépend fortement de la présentation qu'il classe, donc une bonne présentation est requise avant que le k-NN puisse bien fonctionner.

k-NN se différencie par la représentation sur laquelle il agit. De cette façon, nous pouvons directement former le réseau pour classer k-NN. Cela peut être vu comme une sorte de couche de «plus proche voisin» qui agit comme une alternative à softmax.
Nous ne voulons pas mettre en garde contre l'ensemble de nos formations pour chaque mini-soirée, car ce sera une procédure très coûteuse. L'approche adaptée consiste à classer chaque élément du mini-lot en fonction des classes des autres éléments du mini-lot, en donnant à chaque unité de poids divisée par la distance de la cible de classification.

Malheureusement, même avec des architectures complexes, l'utilisation de k-NN réduit la probabilité d'erreur - et l'utilisation d'architectures plus simples dégrade les résultats.

Conclusion

Les propriétés topologiques des données, telles que les relations, peuvent rendre impossible la division linéaire des classes en utilisant des réseaux de faible dimension, quelle que soit la profondeur. Même dans les cas où cela est techniquement possible. Par exemple, les spirales, qu'il peut être très difficile de séparer.

Pour une classification précise des données, les réseaux de neurones ont besoin de larges couches. De plus, les couches traditionnelles du réseau neuronal sont mal adaptées pour représenter des manipulations importantes avec des variétés; même si nous réglons les poids manuellement, il serait difficile de représenter de manière compacte les transformations que nous voulons.