Apprenez OpenGL. Leçon 5.6 - Mappage de parallaxe

Mappage de parallaxe

La technique de texturation du mappage de parallaxe est quelque peu similaire en effet au mappage normal , mais est basée sur un principe différent. La similitude est que, comme la cartographie normale, cette technique augmente considérablement la complexité visuelle et les détails de la surface avec la texture appliquée en créant en même temps une illusion plausible de la présence de différences de hauteur sur la surface. Parallax Mapping fonctionne très bien en conjonction avec Normal Mapping pour créer des résultats très fiables: la technique décrite transmet l'effet de relief beaucoup mieux que Normal Mapping, et Normal Mapping le complète pour une simulation plausible de l'éclairage dynamique. La cartographie de parallaxe peut difficilement être considérée comme une technique directement liée aux méthodes de simulation d'éclairage, mais j'ai néanmoins choisi cette section pour la considérer, car la méthode est un développement logique des idées de la cartographie normale. Je note également que pour analyser cet article, une bonne compréhension de l'algorithme de mappage normal est requise, en particulier le concept d'espace tangent ou d' espace tangent .


Le mappage de parallaxe appartient à la famille des mappages de déplacement ou des techniques de textures en relief qui compensent les sommets d'une géométrie en fonction des valeurs stockées dans des textures spéciales. Par exemple, imaginez un plan composé de l'ordre de mille sommets. Chacun d'eux peut être décalé en fonction de la valeur lue dans la texture, qui représente la hauteur du plan à un point donné. Une telle texture, contenant les valeurs de hauteur dans chaque texel, est appelée une carte de hauteur . Un exemple d'une telle carte, obtenue à partir des caractéristiques géométriques de la surface de la maçonnerie, est l'image suivante:


En échantillonnant à partir de cette carte et en décalant chaque sommet en fonction de la valeur de la hauteur, il est possible d'obtenir une surface convexe à partir d'un plan idéal qui répète les paramètres géométriques de la surface d'origine. Ainsi, en prenant un avion avec un nombre suffisant de sommets et en appliquant une carte de hauteur de l'exemple, vous pouvez obtenir le résultat suivant:


L'approche décrite est simple et facile à mettre en œuvre, mais nécessite une densité élevée de sommets dans l'objet traité, sinon le résultat du décalage sera trop grossier. Et si sur chaque surface plane nous commençons à libérer un millier de sommets ou plus, alors très vite nous n'aurons tout simplement pas le temps de rendre tout ce dont nous avons besoin. Peut-être existe-t-il un algorithme qui vous permet de simuler qualitativement la qualité de l'algorithme de cartographie de déplacement naïf, mais sans nécessiter de tels coûts de géométrie? Si vous vous levez, asseyez-vous, car dans l'image ci-dessus, il n'y a en fait que six sommets (deux triangles)! Le relief de la brique est parfaitement imité grâce à l'utilisation de Parallax Mapping, une technique de texturation en relief qui ne nécessite pas beaucoup de sommets pour transmettre fidèlement le relief de surface, mais, comme Normal Mapping, qui utilise une approche originale pour tromper les yeux de l'observateur.

L'idée principale de la mise en œuvre est de déformer les coordonnées de texture du fragment actuel en fonction de la direction du regard et des données de la carte de la hauteur afin de créer l'illusion que ce fragment appartient à une partie de la surface située plus haut ou plus bas qu'il ne l'est réellement. Pour une meilleure compréhension du principe, regardez le schéma de notre exemple avec des briques:

Ici, la ligne rouge approximative représente les valeurs de la carte de hauteur, reflétant les caractéristiques géométriques de la surface de maçonnerie simulée. Vecteur $$$\ color {orange} {\ bar {V}}$ représente la direction de la surface vers l'observateur ( viewDir ). Si l'avion était vraiment en relief, l'observateur verrait un point à la surface $$$\ color {blue} B$ . Cependant, en fait, nous avons un plan idéal et le rayon dans la direction de la vue traverse le plan en un point $$$\ color {green} A$ c'est évident. Tâche de mappage de parallaxe pour déplacer les coordonnées de texture en un point $$$\ color {green} A$ de sorte qu'ils deviennent identiques aux coordonnées correspondant au point $$$\ color {blue} B$ . Plus loin pour le fragment actuel (correspond au point $$$\ color {green} A$ ) on utilise les coordonnées obtenues du point $$$\ color {blue} B$ l'échantillonnage de texture est nécessaire pour tous, ce qui crée l'illusion que l'observateur voit un point $$$\ color {blue} B$ .

La principale difficulté réside dans la façon de calculer les coordonnées de texture d'un point $$$\ color {blue} B$ être au point $$$\ color {green} A$ . Parallax Mapping offre une solution approximative utilisant une simple mise à l'échelle du vecteur de direction à partir de la surface $$$\ color {orange} {\ bar {V}}$ à l'observateur par la hauteur du fragment $$$\ color {green} A$ . C'est-à-dire il suffit de changer la longueur $$$\ color {orange} {\ bar {V}}$ de sorte qu'il corresponde à la taille de l'échantillon de la carte de hauteur $$$\ color {green} {H (A)}$ correspondant au fragment $$$\ color {green} A$ . Le diagramme ci-dessous montre le résultat de la mise à l'échelle - vecteur $$$\ color {brown} {\ bar {P}}$ :


Ensuite, le vecteur résultant $$$\ color {brown} {\ bar {P}}$ décomposé en composants conformément au système de coordonnées du plan lui-même, qui sont utilisés comme décalages pour les coordonnées de texture d'origine. De plus, puisque le vecteur $$$\ color {brown} {\ bar {P}}$ est calculé en utilisant la valeur de la carte de hauteur, plus la valeur de hauteur correspond au fragment actuel, plus le décalage sera fort pour lui.

Cette technique simple donne de bons résultats dans certains cas, mais il s'agit toujours d'une estimation très approximative de la position d'un point $$$\ color {blue} B$ . Si la carte de hauteur contient des zones dont les valeurs changent fortement, le résultat du déplacement devient incorrect: le vecteur est probablement $$$\ color {brown} {\ bar {P}}$ même proche ne tombera pas à proximité du point $$$\ color {blue} B$ :

Sur la base de ce qui précède, une autre question demeure: comment déterminer comment projeter correctement un vecteur $$$\ color {brown} {\ bar {P}}$ à une surface orientée arbitrairement pour obtenir des composants pour compenser les coordonnées de texture? Ce serait bien de faire des calculs dans un certain système de coordonnées, où l'expansion du vecteur $$$\ color {brown} {\ bar {P}}$ sur les composantes x et y correspondraient toujours à la base du système de coordonnées de texture. Si vous avez soigneusement élaboré la leçon sur la cartographie normale , vous avez déjà deviné que nous parlons de calculs dans l'espace tangent.

Transfert du vecteur de la surface à l'observateur $$$\ color {orange} {\ bar {V}}$ dans l'espace tangent, nous obtenons un vecteur modifié $$$\ color {brown} {\ bar {P}}$ , dont la décomposition en composantes sera toujours effectuée en fonction des vecteurs tangents et bi-tangents pour une surface donnée. Étant donné que la tangente et la bi-tangente sont toujours alignées avec les axes du système de coordonnées de texture de la surface, vous pouvez utiliser les composants x et y du vecteur en toute sécurité, quelle que soit l'orientation de la surface. $$$\ color {brown} {\ bar {P}}$ comme décalages pour les coordonnées de texture.

Cependant, la théorie est suffisante et, ayant retroussé nos manches, nous nous tournons vers la mise en œuvre immédiate.

Mappage de parallaxe

Pour la mise en œuvre, nous utiliserons un plan simple avec des tangentes et des tangentes de biais calculées pour cela - nous pouvons déjà le faire à partir de la leçon sur le mappage normal. Nous attribuons un certain nombre de plans aux plans de texture: diffus , normaux et décalages , chacun étant disponible sur le lien approprié. Dans la leçon, nous utiliserons également le mappage normal, car le mappage parallaxe crée l'illusion d'une topographie de surface, qui est facilement cassée si l'éclairage ne change pas en fonction de la topographie. Étant donné que les cartes normales sont souvent créées sur la base de cartes d'élévation, leur utilisation combinée garantit la bonne connexion de l'éclairage, en tenant compte du terrain.

Vous avez probablement déjà remarqué que la carte de déplacement montrée dans le lien ci-dessus est, en fait, l'inverse de la carte montrée au début de la leçon. L'implémentation de Parallax Mapping est généralement effectuée à l'aide de telles cartes, qui sont inverses aux cartes de hauteur - cartes de profondeur . Cela se produit parce que l'imitation des évidements sur le plan est un peu plus facile que l'imitation de l'élévation. Conformément à ce changement, le schéma de travail de mappage de Parallax change également:


Encore une fois, nous voyons des points familiers $$$\ color {green} A$ et $$$\ color {blue} B$ cependant, cette fois, le vecteur $$$\ color {brown} {\ bar {P}}$ obtenu en soustrayant le vecteur $$$\ color {orange} {\ bar {V}}$ à partir des coordonnées de texture en un point $$$\ color {green} A$ . Les profondeurs au lieu des hauteurs peuvent être obtenues simplement en soustrayant l'échantillon de profondeur de l'unité ou en inversant les couleurs de texture dans n'importe quel éditeur d'image.

Le mappage de parallaxe est implémenté dans le shader de fragments, car les données d'élévation sont différentes pour chaque fragment à l'intérieur du triangle. Le code de shader de fragment nécessitera le calcul du vecteur du fragment à l'observateur $$$\ color {orange} {\ bar {V}}$ , vous devez donc lui transmettre la position du fragment et de l'observateur dans l'espace tangent. Selon les résultats de la leçon sur la cartographie normale, nous avons toujours le vertex shader dans nos mains, qui transfère tous ces vecteurs déjà réduits à l'espace tangent, nous allons l'utiliser:

#version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform mat4 projection; uniform mat4 view; uniform mat4 model; uniform vec3 lightPos; uniform vec3 viewPos; void main() { gl_Position = projection * view * model * vec4(aPos, 1.0); vs_out.FragPos = vec3(model * vec4(aPos, 1.0)); vs_out.TexCoords = aTexCoords; vec3 T = normalize(mat3(model) * aTangent); vec3 B = normalize(mat3(model) * aBitangent); vec3 N = normalize(mat3(model) * aNormal); mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vs_out.FragPos; } 

Parmi les choses importantes, je noterai seulement que spécifiquement pour les besoins de Parallax Mapping, il est nécessaire de transférer le positionPoser dans l'espace tangent vers le fragment shader aPos .

À l'intérieur du shader, nous implémentons l'algorithme de mappage de parallaxe, qui ressemble à ceci:

 #version 330 core out vec4 FragColor; in VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } fs_in; uniform sampler2D diffuseMap; uniform sampler2D normalMap; uniform sampler2D depthMap; uniform float height_scale; vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir); void main() { vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos); //       Parallax Mapping vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); //      //     vec3 diffuse = texture(diffuseMap, texCoords); vec3 normal = texture(normalMap, texCoords); normal = normalize(normal * 2.0 - 1.0); //  –     [...] } 

Nous avons annoncé la fonction ParallaxMapping, qui prend les coordonnées de texture du fragment et du vecteur du fragment à l'observateur $$$\ color {orange} {\ bar {V}}$ dans l'espace tangent. Le résultat de la fonction est des coordonnées de texture décalées, qui sont déjà utilisées pour les échantillons d'une texture diffuse et d'une carte normale. En conséquence, la couleur diffuse du pixel et sa normale correspondent correctement à la «géométrie» modifiée du plan.

Qu'est-ce qui se cache à l'intérieur de la fonction ParallaxMapping?

  vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { float height = texture(depthMap, texCoords).r; vec2 p = viewDir.xy / viewDir.z * (height * height_scale); return texCoords - p; } 

Cette fonction relativement simple est une implémentation littérale de la méthode, dont nous avons discuté ci-dessus les principaux points. Les coordonnées de texture initiales de TexCoords sont prises , à l'aide desquelles la hauteur (ou la profondeur) est sélectionnée $$$\ color {green} {H (A)}$ à partir de depthMap pour le fragment actuel. Pour calculer le vecteur $$$\ color {brown} {\ bar {P}}$ le vecteur viewDir est pris dans l'espace tangent et la paire de ses composantes x et y est divisée par la composante z , et le résultat est mis à l'échelle par la valeur de décalage de lecture de la hauteur . L' uniforme scale_scale a également été introduit pour fournir un contrôle supplémentaire sur la gravité de l'effet de mappage de parallaxe, car l'effet de déplacement est généralement trop fort. Pour obtenir le résultat, on soustrait le vecteur résultant $$$\ color {brown} {\ bar {P}}$ à partir des coordonnées de texture d'origine.

Nous traiterons du moment de la division de viewDir.xy en viewDir.z . Puisque le vecteur viewDir est normalisé, sa composante z se situe dans l'intervalle [0, 1]. Lorsque le vecteur est presque parallèle à la surface du composant z est proche de zéro et que l'opération de division renvoie le vecteur $$$\ color {brown} {\ bar {P}}$ beaucoup plus longtemps que si viewDir est proche de la perpendiculaire à la surface. En d'autres termes, nous mettons à l'échelle le vecteur $$$\ color {brown} {\ bar {P}}$ de sorte qu'il augmente lorsque vous regardez la surface sous un angle - cela vous permet d'obtenir un résultat plus réaliste dans de tels cas.

Certains développeurs préfèrent supprimer la mise à l'échelle en divisant par viewDir.z , car, dans certains cas, cette approche donne des résultats incorrects lorsqu'elle est vue sous un angle. Cette modification de la technique est appelée Parallax Mapping with Offset Limiting . Le choix d'une option d'approche, pour la plupart, reste une question de préférence personnelle - par exemple, je suis plus fidèle aux résultats de l'algorithme de mappage Parallax habituel.

Les coordonnées de texture modifiées résultantes sont finalement utilisées pour sélectionner à partir de la carte diffuse et de la carte normale, ce qui nous donne un assez bon effet de distorsion de surface (le paramètre height_scale ici est choisi proche de 0,1):


Dans l'image, vous pouvez comparer les effets des techniques Normal Mapping et Parallax Mapping. Puisque Parallax Mapping simule des irrégularités de surface, des situations sont possibles pour cette technique où les briques se chevauchent, selon la direction de l'œil.

D'étranges artefacts sont également visibles le long des bordures du plan texturé. Ils apparaissent en raison du fait que les coordonnées de texture décalées par l'algorithme de mappage de parallaxe peuvent tomber en dehors de l'intervalle unitaire et, selon le mode d'habillage , provoquer des résultats indésirables. Un moyen simple de se débarrasser de ces artefacts est de simplement jeter tous les fragments dont les coordonnées de texture sont en dehors de l'intervalle d'unité:

 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0) discard; 

En conséquence, tous les fragments avec des coordonnées de texture décalées tombant de l'intervalle [0, 1] seront rejetés et visuellement le résultat de l'action de mappage de parallaxe deviendra acceptable. De toute évidence, cette méthode de rejet n'est pas universelle et peut ne pas être applicable à certaines surfaces ou cas de texturation. Mais sur l'exemple d'un avion, il fonctionne parfaitement et contribue à renforcer l'effet de modification du relief de l'avion:


Des exemples de sources sont ici .

Il semble bon, et les performances de la méthode sont excellentes - tout ce qu'il a fallu était un échantillon supplémentaire de la texture! Mais la simplicité de la méthode présente des inconvénients importants: l'effet de relief est facilement détruit en regardant l'avion sous un angle (ce qui est également vrai pour la cartographie normale) ou s'il y a des sections dans la carte de hauteur avec des changements brusques de valeurs:


La raison de la destruction de l'illusion réside dans le fait que l'algorithme est une approximation très approximative de la cartographie de déplacement réelle. Cependant, plusieurs astuces supplémentaires peuvent nous aider, ce qui nous permet d'obtenir des résultats presque parfaits même lorsque vous regardez un angle ou lorsque vous utilisez des cartes de hauteur avec des changements brusques. Par exemple, nous pouvons utiliser plusieurs échantillons d'une carte de hauteur afin de trouver le point le plus proche du point $$$\ color {blue} B$ .

Cartographie de parallaxe abrupte

La technique Steep Parallax Mapping est un développement logique du Parallax Mapping classique: la même approche est utilisée dans l'algorithme, mais au lieu d'une seule sélection, plusieurs sont prises - pour une meilleure approximation du vecteur $$$\ color {brown} {\ bar {P}}$ utilisé pour calculer le point $$$\ color {blue} B$ . En raison de ces échantillons supplémentaires, le résultat de l'algorithme est visuellement beaucoup plus plausible, même lorsque l'on regarde des angles vifs par rapport à la surface.

La base de l'approche Steep PM est de prendre une certaine gamme de profondeurs et de la diviser en couches de taille égale. Ensuite, nous parcourons les couches tout en déplaçant simultanément les coordonnées de la texture d'origine dans la direction du vecteur $$$\ color {brown} {\ bar {P}}$ et faire des échantillons à partir de la carte de profondeur, en s'arrêtant au moment où la profondeur de l'échantillon est inférieure à la profondeur de la couche actuelle. Consultez le schéma:


Comme vous pouvez le voir, nous nous déplaçons à travers les couches de haut en bas et pour chaque couche, nous comparons sa profondeur avec la valeur de la carte de profondeur. Si la profondeur de couche est inférieure à la valeur de la carte de profondeur, cela signifie que le vecteur $$$\ color {brown} {\ bar {P}}$ correspondant à cette couche se trouve au-dessus de la surface. Ce processus est répété jusqu'à ce que la profondeur de la couche soit supérieure à la sélection de la carte de profondeur: à ce moment, le vecteur $$$\ color {brown} {\ bar {P}}$ pointe vers un point en dessous de la topographie de surface simulée.
L'exemple montre que la sélection à partir de la carte de profondeur sur la deuxième couche ( $$$D (2) = 0,73$ ) se situe toujours «plus profondément» par rapport à la profondeur de la deuxième couche égale à 0,4, ce qui signifie que le processus de recherche se poursuit. Dans la passe suivante, une profondeur de couche de 0,6 se révèle finalement être «supérieure» à la valeur de l'échantillon de la carte de profondeur ( $$$D (3) = 0,37$ ) De là, nous concluons que le vecteur $$$\ color {brown} {\ bar {P}}$ obtenue pour la troisième couche est la position la plus fiable pour la géométrie de surface déformée. Vous pouvez utiliser des coordonnées de texture $$$T_3$ dérivé du vecteur $$$\ color {brown} {\ bar {P}}$ , pour décaler les coordonnées de texture du fragment actuel. De toute évidence, la précision de la méthode augmente avec le nombre de couches.

Les changements dans l'implémentation n'affecteront que la fonction ParallaxMapping, car elle contient déjà toutes les variables nécessaires au fonctionnement de l'algorithme:

 vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { //    const float numLayers = 10; //    float layerDepth = 1.0 / numLayers; //    float currentLayerDepth = 0.0; //         //     P vec2 P = viewDir.xy * height_scale; vec2 deltaTexCoords = P / numLayers; [...] } 

Tout d'abord, nous initialisons: définissons le nombre de couches, calculons la profondeur de chacune d'elles et, enfin, trouvons la taille du déplacement des coordonnées de texture le long de la direction du vecteur $$$\ color {brown} {\ bar {P}}$ , qui devra être décalé sur chaque couche.

Ensuite, un passage à travers les couches, en commençant par le haut, jusqu'à ce qu'une sélection de la carte de profondeur se trouve «au-dessus» de la valeur de profondeur de la couche actuelle:

 //   vec2 currentTexCoords = texCoords; float currentDepthMapValue = texture(depthMap, currentTexCoords).r; while(currentLayerDepth < currentDepthMapValue) { //      P currentTexCoords -= deltaTexCoords; //          currentDepthMapValue = texture(depthMap, currentTexCoords).r; //     currentLayerDepth += layerDepth; } return currentTexCoords; 

Dans ce code, nous traversons toutes les couches de profondeur et décalons les coordonnées de texture d'origine jusqu'à ce que la sélection à partir de la carte de profondeur soit inférieure à la profondeur de la couche actuelle. Le décalage est effectué en soustrayant des coordonnées de texture d'origine du delta sur la base du vecteur $$$\ color {brown} {\ bar {P}}$ . Le résultat de l'algorithme est un vecteur de décalage de coordonnées de texture, défini avec une précision beaucoup plus grande que le Parallax Mapping classique.

En utilisant environ 10 échantillons, l'exemple de maçonnerie devient beaucoup plus réaliste, même vu sous un angle. Mais le meilleur de tous, les avantages de Steep PM sont visibles sur les surfaces avec une carte de profondeur, qui a de brusques changements de valeurs. Par exemple, comme sur ce jouet en bois, déjà démontré précédemment:


Vous pouvez améliorer un peu plus l'algorithme si vous analysez un peu les caractéristiques de la technique de mappage de parallaxe. Si vous regardez la surface à peu près normale, il n'est pas nécessaire de modifier fortement les coordonnées de la texture, tandis que lorsque vous regardez un angle, le décalage tend vers le maximum (imaginez mentalement la direction de la vue dans les deux cas). Si vous paramétrez le nombre d'échantillons en fonction de la direction de votre regard, vous pouvez économiser beaucoup lorsque des échantillons supplémentaires ne sont pas nécessaires:

 const float minLayers = 8.0; const float maxLayers = 32.0; float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir))); 

Le résultat du produit scalaire du vecteur viewDir et du demi-axe positif Z est utilisé pour déterminer le nombre de couches dans l'intervalle [ minSamples , maxSamples ], c'est-à-dire la direction du regard détermine le nombre requis d'itérations de l'effet (dans l'espace tangent, le demi-axe positif Z est dirigé perpendiculairement à la surface). Si nous regardions parallèlement à la surface, l'effet utiliserait les 32 couches.

Le code source modifié est ici . Je propose également de télécharger la texture d'un jouet en bois: diffuse , carte normale, carte de profondeur .

Non sans approche et inconvénients. Comme le nombre d'échantillons est tout de même fini, l'apparition d'effets de repliement est inévitable, ce qui rend les transitions entre les couches frappantes:


Vous pouvez réduire la gravité de l'artefact en augmentant le nombre d'échantillons utilisés, mais il consomme assez rapidement toutes les performances du processeur vidéo disponibles. Il y a plusieurs ajouts à la méthode, qui retournent par conséquent non pas le premier point qui est apparu sous le relief imaginaire de la surface, mais la valeur interpolée des deux couches les plus proches, ce qui nous permet de clarifier davantage la position du point $$$\ color {blue} B$ .

Parmi ces méthodes, deux sont le plus souvent utilisées: Relief Parallax Mapping et Parallax Occlusion Mapping , Relief PM donnant les résultats les plus fiables, mais il est également légèrement plus exigeant en termes de performances par rapport au Parallax Occlusion Mapping. Comme Parallax Occlusion Mapping est encore assez proche de Relief PM et fonctionne en même temps plus rapidement, ils préfèrent l'utiliser le plus souvent. Ensuite, l'implémentation de Parallax Occlusion Mapping sera considérée.

Cartographie d'occlusion Parallax

La méthode Parallax Occlusion Mapping fonctionne sur les mêmes principes de base que Steep PM, mais au lieu d'utiliser les coordonnées de texture de la première couche, où une intersection avec un relief imaginaire a été trouvée, la méthode utilise une interpolation linéaire entre deux couches: la couche après et avant l'intersection. Le coefficient de pondération pour l'interpolation linéaire est basé sur le rapport de la profondeur de relief actuelle aux profondeurs des deux couches considérées. Jetez un œil au diagramme pour mieux comprendre comment tout fonctionne:


Comme vous pouvez le voir, tout est très similaire à Steep PM, une seule étape supplémentaire d'interpolation des coordonnées de texture des deux couches de profondeur adjacentes au point d'intersection est ajoutée. Bien sûr, une telle méthode n'est qu'une approximation, mais beaucoup plus précise que Steep PM.

Le code Parallax Occlusion Mapping est en plus du code Steep PM et n'est pas trop compliqué:

 [...] // ,    Steep PM //       , // ..  " " vec2 prevTexCoords = currentTexCoords + deltaTexCoords; //         //      float afterDepth = currentDepthMapValue - currentLayerDepth; float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth; //    float weight = afterDepth / (afterDepth - beforeDepth); vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight); return finalTexCoords; 

Au moment de trouver la couche située après le point d'intersection avec le relief imaginaire, nous déterminons également les coordonnées de texture de la couche située avant le point d'intersection. Ensuite, nous trouvons les déplacements de la profondeur de relief imaginaire par rapport aux profondeurs des deux couches considérées et utilisons leur rapport comme coefficient de poids d'une interpolation linéaire supplémentaire des coordonnées de texture correspondant aux deux couches considérées. Le résultat de l'interpolation est renvoyé par la fonction pour une utilisation future.

La cartographie d'occlusion Parallax donne des résultats visuellement étonnamment fiables, mais avec de petits défauts et des artefacts de repliement. Mais pour un compromis de vitesse et de qualité, ils sont insignifiants et n'apparaissent qu'avec une observation rapprochée de la surface proche de la caméra ou sous des angles de vision très précis.


Un exemple de code est ici .

Le mappage de parallaxe est vraiment une excellente technique qui vous permet d'augmenter considérablement les détails visuels de votre scène, mais, bien sûr, a ses inconvénients sous la forme d'artefacts, ce qui mérite d'être rappelé lors de la mise en œuvre de la technique dans le projet. Pour la plupart, Parallax Mapping est utilisé sur des surfaces planes telles que les murs ou les sols - où il n'est pas si facile de déterminer le contour de l'objet dans son ensemble, et l'angle de vue de la surface est souvent proche de la perpendiculaire. Dans ce cas, les défauts de mappage de parallaxe sont presque invisibles, sur fond de détails de surface accrus.

Bonus du traducteur:

Cartographie de parallaxe en relief

Puisque l'auteur a mentionné deux méthodes pour clarifier le résultat de Steep PM, pour être complet, je décrirai la seconde des approches.

Comme Parallax Occlusion Mapping, le résultat de l'exécution de Steep PM est utilisé ici, c'est-à-dire on connaît les profondeurs de deux couches entre lesquelles se situe le vrai point d'intersection du vecteur $$$\ color {orange} {\ bar {V}}$ avec relief, ainsi que les coordonnées de texture correspondantes $$$T_2$ et $$$T_3$ . Le raffinement de l'estimation du point d'intersection dans cette méthode est dû à l'utilisation de la recherche binaire.

Étapes de l'algorithme de raffinement:

• Effectuer un calcul de PM raide et obtenir des coordonnées de texture $$$T_2$ et $$$T_3$ - dans cet intervalle se trouve le point d'intersection du vecteur $$$\ color {green} {\ bar {V}}$ avec topographie de surface. La véritable intersection est marquée d'une croix rouge.
• Divisez en deux valeurs actuelles pour le décalage des coordonnées de texture et la hauteur de la couche de profondeur.
• Déplacer les coordonnées de texture du point $$$T_3$ dans la direction opposée au vecteur $$$\ color {green} {\ bar {V}}$ par la quantité de déplacement. Réduisez la profondeur du calque de la valeur de taille de calque actuelle.
• Recherche directement binaire. Le nombre d'itérations spécifié est répété:
• 1. Sélectionnez dans la carte de profondeur. Divisez le décalage de texture actuel et la taille du calque de profondeur en deux valeurs actuelles.
  2. Si la taille de l'échantillon est supérieure à la profondeur de couche actuelle, augmentez la profondeur de couche de la taille de couche actuelle et modifiez les coordonnées de texture le long du vecteur $$$\ color {green} {\ bar {V}}$ au décalage actuel.
  3. Si la taille de l'échantillon est inférieure à la profondeur de couche actuelle, réduisez la profondeur de couche de la taille de couche actuelle et modifiez les coordonnées de texture le long du vecteur inverse $$$\ color {green} {\ bar {V}}$ au décalage actuel.
  
  
• Les dernières coordonnées de texture obtenues sont les résultats de Relief PM.

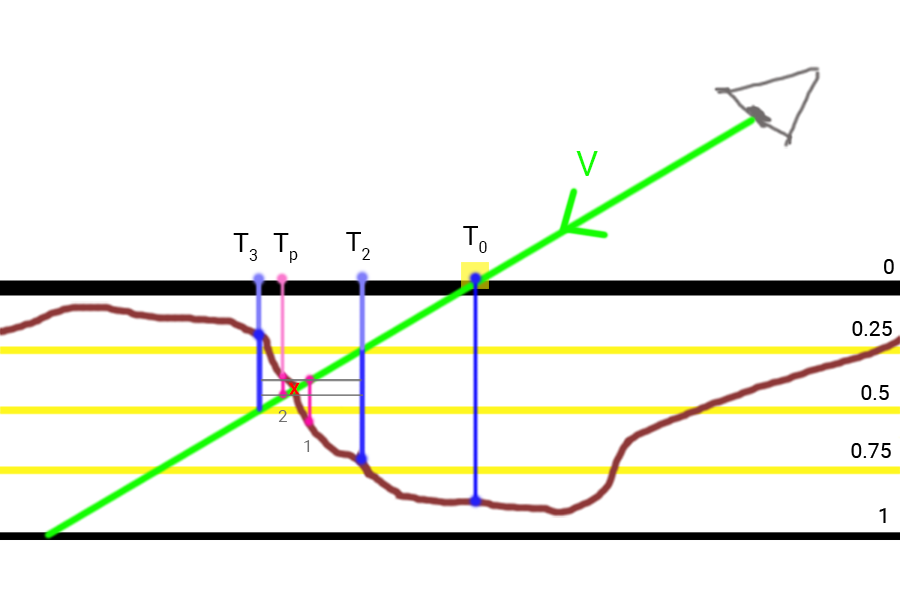
L'image montre qu'après avoir trouvé les points $$$T_2$ et $$$T_3$ nous divisons par deux la taille du calque et la taille du décalage des coordonnées de texture, ce qui nous donne le premier point d'itération de la recherche binaire (1). Étant donné que la taille de l'échantillon qu'il contient s'est avérée être plus grande que la profondeur actuelle de la couche, nous avons à nouveau divisé par deux les paramètres et nous avons avancé $$$\ color {green} {\ bar {V}}$ obtenir le point (2) avec les coordonnées de texture $$$T_p$ qui sera le résultat de Steep PM pour deux itérations de la recherche binaire.

Code de shader:

 //  : inTexCoords -   , // inViewDir -      - //  : lastDepthValue –      //      vec2 reliefPM(vec2 inTexCoords, vec3 inViewDir, out float lastDepthValue) { // ====== // ,   Steep PM // ====== const float _minLayers = 2.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(dot(vec3(0., 0., 1.), inViewDir))); float deltaDepth = 1./_numLayers; // uDepthScale –     PM vec2 deltaTexcoord = uDepthScale * inViewDir.xy/(inViewDir.z * _numLayers); vec2 currentTexCoords = inTexCoords; float currentLayerDepth = 0.; float currentDepthValue = depthValue(currentTexCoords); while (currentDepthValue > currentLayerDepth) { currentLayerDepth += deltaDepth; currentTexCoords -= deltaTexcoord; currentDepthValue = depthValue(currentTexCoords); } // ====== //   Relief PM // ====== //         deltaTexcoord *= 0.5; deltaDepth *= 0.5; //      ,   Steep PM currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; //    … const int _reliefSteps = 5; int currentStep = _reliefSteps; while (currentStep > 0) { currentDepthValue = depthValue(currentTexCoords); deltaTexcoord *= 0.5; deltaDepth *= 0.5; //       , //       if (currentDepthValue > currentLayerDepth) { currentTexCoords -= deltaTexcoord; currentLayerDepth += deltaDepth; } //       else { currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; } currentStep--; } lastDepthValue = currentDepthValue; return currentTexCoords; } 

Auto-observation

Également un petit ajout sur l'ajout d'ombrage d'une source de lumière sélectionnée à l'algorithme de calcul. J'ai décidé d'ajouter, car techniquement la méthode de calcul est identique à celles considérées ci-dessus, mais l'effet reste intéressant et ajoute des détails.

En fait, le même PM raide est appliqué, mais la recherche n'entre pas profondément dans la surface simulée le long de la ligne de visée, mais de la surface, le long du vecteur jusqu'à la source de lumière$$$\color{green}{\bar{L}}$ .Ce vecteur est également transféré dans l'espace tangent et est utilisé pour déterminer la quantité de déplacement des coordonnées de texture. En sortie du procédé, un coefficient d'éclairage du matériau est obtenu dans l'intervalle [0, 1], qui est utilisé pour moduler les composants diffus et miroir dans les calculs d'éclairage.
Pour définir un ombrage avec des arêtes vives, il suffit de marcher le long du vecteur$$ˉ L jusqu'à ce qu'un point se trouve sous la surface. Dès qu'un tel point est trouvé, nous prenons le coefficient d'éclairage 0. Si nous atteignons une profondeur nulle sans rencontrer un point situé sous la surface, alors nous prenons le coefficient d'éclairage égal à 1.Pour déterminer l'ombrage avec des bords doux, il est nécessaire de vérifier plusieurs points se trouvant sur le vecteur$\color{green}{\bar{L}}$

$$ˉ L et situé sous la surface. Le facteur d'ombrage est pris égal à la différence entre la profondeur de la couche actuelle et la profondeur de la carte de profondeur. La suppression du point suivant du fragment en question est également prise en compte sous la forme d'un coefficient de pondération égal à (1,0 - stepIndex / numberOfSteps). À chaque étape, un coefficient d'éclairage partiel est déterminé comme suit:$\color{green}{\bar{L}}$

$$

$$PSF_i=(layerHeight_i - heightFromtexture_i)*(1.0-\frac{i}{numSteps})$$

Le résultat final est le facteur de lumière maximum de tout partiel:

$$

$$SF=max(PSF_i)$$

Le schéma de la méthode:

Progression de la méthode pour trois itérations dans cet exemple:

• Nous initialisons le facteur de lumière total à zéro.
• Faites un pas le long du vecteur $$ˉ L , aller droit au but$\color{green}{\bar{L}}$$$$H_a$ . La profondeur du point est nettement inférieure à la sélection sur la carte. $$H ( T L 1 ) - il est sous la surface. Ici, nous avons fait le premier contrôle et, en se souvenant du nombre total de contrôles, nous trouvons et enregistrons le premier facteur de lumière partiel: (1.0 - 1.0 / 3.0).$H(T_{L1})$
• Faites un pas le long du vecteur $$ˉ L , aller droit au but$\color{green}{\bar{L}}$$$$H_b$ . La profondeur du point est nettement inférieure à la sélection sur la carte. $$H ( T L 2 ) - il est sous la surface. Le deuxième contrôle et le deuxième coefficient partiel: (1.0 - 2.0 / 3.0).$H(T_{L2})$
• Nous faisons un pas de plus le long du vecteur et atteignons la profondeur minimale de 0. Arrêtez le mouvement.
• Définition du résultat: si aucun point n'a été trouvé sous la surface, on renvoie un coefficient égal à 1 (pas d'ombrage). Sinon, le coefficient résultant devient le maximum des coefficients partiels calculés. Pour une utilisation dans les calculs d'éclairage, nous soustrayons cette valeur de l'unité.

Exemple de code de shader:

 //  : inTexCoords -   , // inLightDir -       - //  : inLastDepth –    , //      PM //       //    float getParallaxSelfShadow(vec2 inTexCoords, vec3 inLightDir, float inLastDepth) { float shadowMultiplier = 0.; //      , //    float alignFactor = dot(vec3(0., 0., 1.), inLightDir); if (alignFactor > 0.) { //   :  ,  //  ,     const float _minLayers = 16.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(alignFactor)); float _dDepth = inLastDepth/_numLayers; vec2 _dtex = uDepthScale * inLightDir.xy/(inLightDir.z * _numLayers); //  ,    int numSamplesUnderSurface = 0; //       //     L float currentLayerDepth = inLastDepth - _dDepth; vec2 currentTexCoords = inTexCoords + _dtex; float currentDepthValue = depthValue(currentTexCoords); //    float stepIndex = 1.; // ,       … while (currentLayerDepth > 0.) { //     ,     //       if (currentDepthValue < currentLayerDepth) { numSamplesUnderSurface++; float currentShadowMultiplier = (currentLayerDepth - currentDepthValue)*(1. - stepIndex/_numLayers); shadowMultiplier = max(shadowMultiplier, currentShadowMultiplier); } stepIndex++; currentLayerDepth -= _dDepth; currentTexCoords += _dtex; currentDepthValue = depthValue(currentTexCoords); } //      ,   //      1 if (numSamplesUnderSurface < 1) shadowMultiplier = 1.; else shadowMultiplier = 1. - shadowMultiplier; } return shadowMultiplier; } 

Le coefficient résultant est utilisé pour moduler le résultat du modèle d'éclairage Blinn-Fong utilisé dans les exemples:

 [...] //      vec3 fullColorADS = ambientTerm + attenuation * (diffuseTerm + specularTerm); //     -  fullColorADS *= pmShadowMultiplier; return fullColorADS; 

Comparaison de toutes les méthodes dans un collage, volume 3MB.

Aussi une comparaison vidéo:

Matériel supplémentaire

• Cartographie d'occlusion Parallax dans GLSL : Une excellente leçon de cartographie Parallax de sunandblackcat.com .
• Comment fonctionne le mappage de déplacement Parallax : Un didacticiel vidéo qui explique les détails du mappage Parallax par TheBennyBox .

PS : Nous avons un télégramme conf pour la coordination des transferts. Si vous avez un sérieux désir d'aider à la traduction, alors vous êtes les bienvenus!