🙏🏾 🥉 🥕 Formule de Tupper et implémentation de l'algorithme en Python 🤘🏽 🏣 👔

Au lieu de l'avant-propos

Il n'y a pas si longtemps, sur Internet, j'ai découvert une copie aussi merveilleuse et étonnante de la bibliothèque babylonienne que la formule Tapper . C'est plutôt l'inégalité de Tupper que la formule. La particularité de cette inégalité est qu'elle crée sa propre image sur la carte. Regardez ce miracle!

(Source Wikipedia)

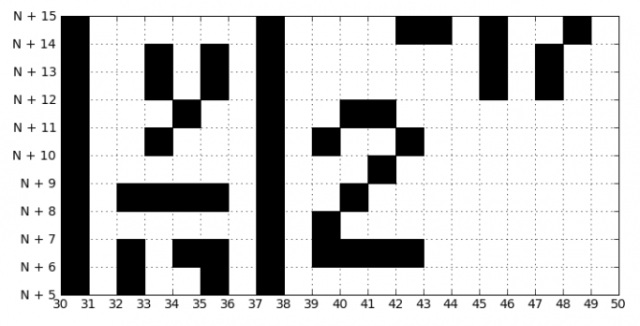
Ce que vous voyez dans l'image est la formule de ce même Jeff Tupper. Probablement, la moitié des lecteurs sont déjà allés au tungstène pour tirer le résultat de cette inégalité ... Mais ce n'est pas si simple. Comme vous pouvez le voir sur cette image, la formule sur le graphique peut être vue sur un segment le long de l'axe OY [k; k + 15]. Quel est ce mystérieux nombre k? Où l'obtenir? Le fait est que cette inégalité, selon le concept de la bibliothèque babylonienne, peut afficher absolument n'importe quelle image avec une résolution de 106x17! Chaque image a sa propre position sur le graphique, a ainsi un numéro unique k. Ainsi, pour chaque nombre k il y a une seule image sur tout le graphe !

Pour une image donnée, le nombre k est le suivant:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

Il est intéressant de regarder les personnes qui défileront jusqu'à une telle coordonnée pour voir la formule

Il m'est venu à l'esprit d'écrire un programme en Python3 qui convertirait une image en un nombre k et vice versa et vous parlerait d'un autre excellent moyen de coder une image en un nombre.

Théorie

(Ajouté) Comment ça marche?

Jetons un coup d'œil à la formule elle-même:

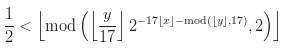
Définissons sa syntaxe:

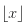
- nombre arrondi
mod (x, y) - reste de la division de x par y

Et puis, semble-t-il, tout est clair.
Notez que x et y sont arrondis. C'est cet arrondi qui nous donne finalement une image pixel

Indique tout ce qui est arrondi à droite de l'inégalité par

$\ alpha$ .
Alors

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

Ce qui est évident, car toute l'expression est arrondie.

Soit y = 17r + q, où r est la partie entière de la division de y par 17, et r est le reste de la division. Ainsi, nous pouvons remplacer dans la formule

$[a / 17]$ sur r, et

$mod (y, 17)$ le q.

Nous obtenons

$1 <= mod (q * 2 ^ {- 17-r}, 2)$

Ou bien

$1 <= mod (q / 2 ^ {17x + r}, 2)$

mod (

$\ alpha$ , 2) prend 2 valeurs - 0 ou 1. Par conséquent, cette inégalité dira si le nombre

$q / 2 ^ {17x + r}$ même ou pas.

Notez que l'image est visualisée dans l'intervalle [N, N + 16], respectivement

$q = [a / 17]$ reste constant sur toute la hauteur de l'image, ce qui ne peut pas être dit du nombre r (sur toute l'image il varie de 0 à 16).

Et maintenant la cerise sur le gâteau. Numéro

$[q / {2 ^ {17x + r}}]$ sera impair si et seulement si le nombre de bits (17x + r) dans la représentation binaire de q est égal à 1. Et comme le nombre q change constamment avec sa hauteur et sa représentation binaire aussi, on obtient une image unique à chaque fois! C'est exactement ce que la formule de Tapper fonctionne.

Voyons maintenant comment calculer la hauteur à laquelle nous voulons voir notre image

Le principe du calcul du nombre k

Tupper lui-même a décrit le calcul du nombre k pour toute image 106x17 (c'est important!) Comme suit:

Convertir l'image en noir et blanc
Lisez chaque pixel de bas en haut, de gauche à droite et mettez-le dans le tampon. Si le pixel est noir - mettez 1, si blanc - 0.
Convertissez le binaire en décimal et multipliez par 17
Profit!

Pour obtenir une image à partir du nombre k, nous faisons tout exactement le contraire. Eh bien, allons coder!

Kodim

UPD: Dans les commentaires, les gens ont un peu amélioré le code, l'ont rendu plus simple et plus transparent. Cet article a publié des données de mise à jour. Si vous voulez voir les anciennes versions du code - allez dans le dépôt github (jusqu'à ce que vous le validiez, lien à la fin de l'article) et dans le commentaire

De k à l'image

UPD

A la demande des commentateurs, une nouvelle méthode a été ajoutée pour calculer l'image en utilisant cette inégalité et k! Maintenant, nous ne ferons pas de manipulations avec le nombre, transférons au système binaire, mais affectons directement la fonction elle-même!

Utilisation de la méthode tapper pour décoder le nombre k

Nous obtenons le nombre k de l'utilisateur, les ~~yeux fermés, nous le~~ divisons par 17 et le traduisons dans le système binaire.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

Nous comprenons que certains pixels initiaux peuvent être blancs (égaux à 0), respectivement, pour notre nombre binaire, les premiers bits seront des zéros et lors de la traduction d'un nombre en système décimal, ces zéros initiaux seront perdus. Par conséquent, nous vérifions la taille du nombre binaire résultant, s'il est inférieur à 1802, puis ajoutons des zéros au début.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

Ensuite, déclarez une liste bidimensionnelle dans laquelle nous stockons des informations sur chaque ligne de l'image. Ensuite, nous notons tous ces bits que nous lisons (n'oubliez pas l'algorithme par lequel le nombre k est créé - de bas en haut, de gauche à droite)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

Essayons de pousser le nombre k, que j'ai indiqué au début de l'article, dans notre programme et obtenons ce qui suit:

Comme vous pouvez le voir, tout a fonctionné pour nous, et maintenant nous pouvons décoder n'importe quel k!

Utiliser l'inégalité pour générer une image à partir de k

Tout d'abord, écrivez la fonction en python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

Grâce aux opérateurs // et <<, l'implémentation de la fonction a été grandement simplifiée. Il est garanti que les nombres x et y seront des entiers !

Nous créons à nouveau une liste à deux dimensions, où nous allons stocker les bits de l'image et écrire des informations sur chaque ligne en utilisant des boucles

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

Et puis, comme dans l'exemple précédent, nous dessinons une image à l'aide de la bibliothèque PIL.

La fonction complète ressemble à ceci:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

Image en k

Eh bien, nous allons maintenant apprendre à coder n'importe quelle image dans le nombre k.

Nous obtenons d'abord l'image elle-même

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

Vérifiez sa taille

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

Nous faisons l'image en noir et blanc et commençons à lire pixel par pixel:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

Il ne reste plus qu'à convertir au système décimal et à multiplier par 17.

 k = int(byteset,2)*17 print(" :") print(k)

Eh bien, allons tester!

J'ai décidé de coder le logo habr. Voici l'image source:

Nous démarrons le programme et spécifions le nom de l'image:

Nous avons obtenu le k suivant:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Voyons cela sur notre propre programme.

Voici l'image que nous avons reçue:

Il était un peu déformé en raison d'une traduction légèrement tordue de l'image en noir et blanc.

Résumé

Code source: Github

Sources: article Wiki

Formule de Tupper et implémentation de l'algorithme en Python