Dans un article récent, «
Modulation d'amplitude d'un signal arbitraire », son auteur a tenté de présenter sa compréhension de la formation du spectre avec la modulation d'amplitude de manière confuse. Mais le manque d'illustrations et un excès de mathématiques impliquant des transformations intégrales ont empêché la communauté de comprendre les pensées de l'auteur et d'apprécier l'article; alors que le sujet est assez simple - et nous essaierons de l'examiner à nouveau, cette fois avec des images et Wolfram Mathematica.
Ainsi, l'idée de la modulation d'amplitude est de transmettre un signal basse fréquence - voix ou musique - modulant un signal haute fréquence (porteuse), dépassant plusieurs fois la plage audible et occupant une bande de fréquence étroite dans l'air. La modulation elle-même s'effectue en multipliant simplement le signal par la porteuse:

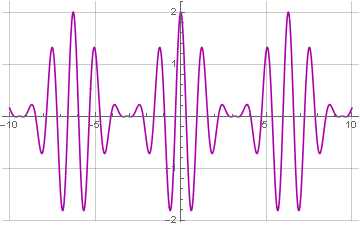
Ici, nous avons une onde sinusoïdale avec une fréquence de 5:


Et le signal lui-même - avec une fréquence de 1:

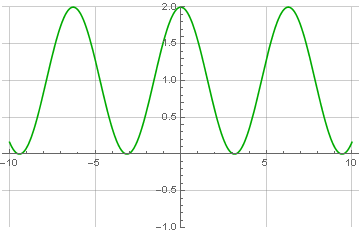
Vous pouvez remarquer que le signal est décalé vers le haut et n'a que des valeurs positives. Ce n'est pas accidentel et est une condition préalable à la possibilité d'une restauration correcte ultérieure. Comment le restaurer? Très simple! Il est nécessaire de décaler la phase du signal modulé de 90 degrés (l'opération connue sous
le nom de
transformée de Hilbert ), et de calculer la racine de la somme des carrés des signaux modulés et convertis:

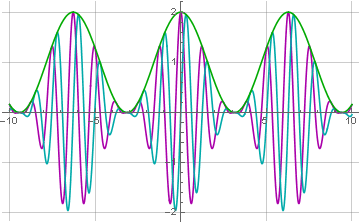
Dans une version plus simple (mais approximative), la transformée de Hilbert peut être remplacée par un retard du signal d'un quart de la période de fréquence de la porteuse, et le signal final peut en outre être filtré par un filtre passe-bas. Dans une version encore plus simple, vous ne pouvez pas du tout compter les racines et les carrés, mais filtrer le signal par la valeur absolue (qui est généralement utilisée dans les récepteurs radio).
Voyons maintenant ce qui se passe avec les spectres. Nous calculons la transformée de Fourier de la porteuse:


Comme la fonction delta de Dirac n'est pas une fonction au sens classique, son graphe ne peut pas être construit de manière standard; par conséquent, nous le ferons manuellement en utilisant le style généralement accepté:

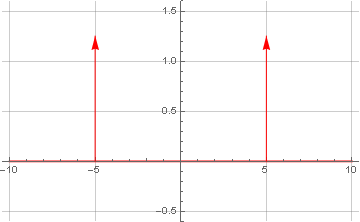
Devrait recevoir la même fréquence que dans la formule initiale. La présence d'une ou plusieurs de la même fréquence, mais avec un signe moins, n'est pas accidentelle - ce phénomène est appelé
symétrie hermitienne et est une conséquence du fait que la fonction en question est purement réelle et dans la représentation complexe a une composante imaginaire nulle. L'absence de composants imaginaires dans le spectre après la transformation est due au fait qu'au départ nos fonctions sont paires (symétriques par rapport à zéro).
Maintenant, nous faisons la transformée de Fourier pour le signal lui-même:



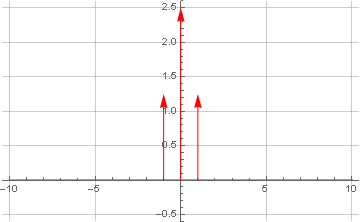
Ici, nous avons également obtenu la fonction delta de Dirac au centre des coordonnées - en raison de la présence d'une composante constante dans le signal, qui n'a pas d'oscillations par définition - ce qui nous permet de la considérer comme une fréquence nulle.
Qu'adviendra-t-il du spectre s'il est multiplié? Voyons voir:



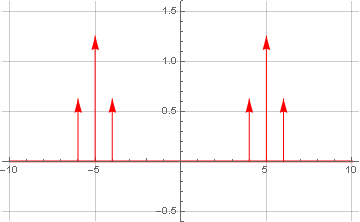
De la théorie, nous savons que la multiplication dans le domaine temporel est équivalente à la convolution dans le domaine fréquentiel (et vice versa, qui est largement utilisée dans le filtrage FIR). Et comme l'un des signaux soumis à la convolution était constitué d'une seule fréquence (positive et négative), alors à la suite de la convolution, nous avons obtenu juste un transfert linéaire du signal vers le haut en fréquence (dans les deux sens). Et puisque la symétrie est restée, le signal n'a toujours pas de composante imaginaire.
Nous le présentons maintenant sous une forme complexe (
analytique ), en mettant à zéro la plage de fréquence négative:

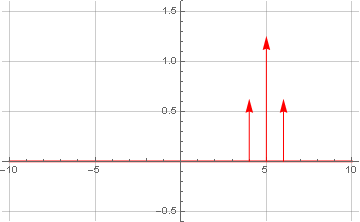
et faire la transformée de Fourier inverse:


La fonction étant désormais complexe, pour construire son graphe, il faut extraire séparément les composants réels et imaginaires:

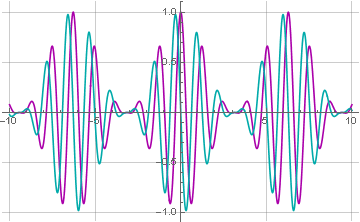
Maintenant, notre signal a une composante imaginaire, qui est le signal d'origine décalé de 90 degrés. Cela sera plus évident si nous représentons la fonction résultante sous une forme trigonométrique:

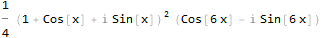
Pas encore très évident. Essayons de simplifier:

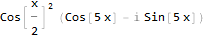
Maintenant, cela ressemble plus à la vérité - et comme vous pouvez le voir, la fonction de notre signal d'origine a également été simplifiée. Essayons de le remettre dans sa forme originale:
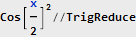

Le facteur 1/2 n'est pas apparu par hasard - après avoir mis à zéro la moitié du spectre, nous avons donc réduit la puissance du signal. Eh bien, maintenant, ayant un signal complexe modulé, nous pouvons prendre ce module pour calculer:

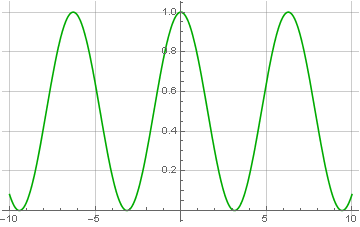
Le module d'un nombre complexe est calculé précisément par la racine de la somme des carrés des composantes imaginaires et réelles. Et à partir de cela, il est clair pourquoi le signal codé ne doit être composé que de valeurs positives - s'il comprend des valeurs négatives, après restauration, elles deviendront également positives, ce qui est appelé surmodulation:

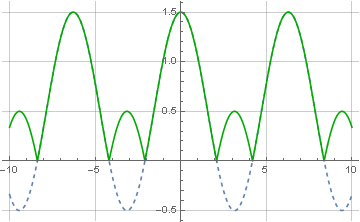
La récupération du signal est également possible à l'aide d'un oscillateur local en quadrature - lorsque le signal modulé est à nouveau multiplié par la fréquence porteuse, mais cette fois, il est complexe:





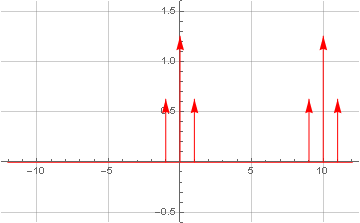
En raison du fait que la fréquence complexe dans le domaine fréquentiel n'a qu'une seule impulsion sans la dupliquer dans la plage de fréquence négative, à la suite de la convolution, nous obtenons un transfert de spectre linéaire, dans lequel la partie négative du spectre revient au centre, et la positive se déplace encore plus loin, et il ne sera filtré que par un filtre passe-bas.
Conclusion
Comme vous pouvez le voir, il n'y a rien de compliqué à considérer la modulation d'amplitude via la transformée de Fourier; si nous le considérons exclusivement au niveau de l'école, il suffit de rappeler que le produit de la somme (porteuse) (représentant le signal sous la forme d'une série trigonométrique) est équivalent à la somme des produits (chaque membre de la série individuellement à la fréquence porteuse) - et, par conséquent, chaque produit est décomposé en la somme de deux sinusoïdes selon la formule déjà exprimée par l'auteur de l'article original.
Un lecteur attentif pourrait également remarquer que puisque la modulation a entraîné un spectre symétrique par rapport à la fréquence porteuse, cela signifie qu'il y a redondance des données et que vous ne pouvez laisser qu'une seule bande latérale, réduisant ainsi la bande de fréquence occupée à l'air. Une telle technologie
existe , mais c'est une histoire complètement différente.