Salutations à tous, et particulièrement à ceux qui s'intéressent aux mathématiques discrètes et à la théorie des graphes.
Contexte
Il se trouve que, poussé par l'intérêt, je développais un service de construction de circuits. itinéraires. La tâche consistait à planifier les meilleurs itinéraires en fonction de la ville d'intérêt pour l'utilisateur, des catégories d'établissements et du calendrier. Eh bien, l'une des sous-tâches consistait à calculer le temps de trajet d'une institution à l'autre. Depuis que j'étais jeune et stupide, j'ai résolu ce problème de front, avec l'algorithme de Dijkstra, mais en toute honnêteté, il convient de noter que seulement avec lui, il était possible de démarrer l'itération d'un nœud à des milliers d'autres, la mise en cache de ces distances n'était pas une option, les établissements de plus de 10k seulement dans Moscou seule, et des décisions comme la distance de Manhattan dans nos villes ne fonctionnent pas du tout.
Il s'est donc avéré qu'il était possible de résoudre le problème de performances dans le problème de la combinatoire, mais la plupart du temps pour traiter la demande était consacrée à la recherche de chemins non mis en cache. Le problème a été compliqué par le fait que le graphique routier Osm à Moscou est assez grand (un demi-million de nœuds et 1,1 million d'arcs).
Je ne parlerai pas de toutes les tentatives et qu'en fait le problème pourrait être résolu en coupant les arcs supplémentaires du graphique, je vais seulement vous dire qu'à un moment donné il m'est apparu et j'ai réalisé que si vous approchez l'algorithme de Dijkstra du point de vue de l'approche probabiliste, il peut être linéaire.
Dijkstra pour le temps logarithmique
Tout le monde sait, mais qui sait, lisez que l'algorithme de Dijkstra en utilisant une file d'attente avec la complexité logarithmique d'insertion et de suppression peut conduire à une complexité de la forme O (n log (n) + m log (n)). Lorsque vous utilisez le tas de Fibonacci, la complexité peut être réduite à O (n * log (n) + m), mais toujours pas linéaire, mais je voudrais.
Dans le cas général, l'algorithme de file d'attente est décrit comme suit:
Soit:
- V est l'ensemble des sommets du graphe
- E est l'ensemble des bords du graphe
- w [i, j] est le poids du bord du nœud i au nœud j
- a - début du sommet de la recherche
- file d'attente q-vertex
- d [i] - distance jusqu'au i-ème nœud
- d [a] = 0, pour tous les autres d [i] = + inf
Alors que q n'est pas vide:
- v est le sommet avec le minimum d [v] de q
- Pour tous les sommets u pour lesquels il existe une transition vers E à partir du sommet v
- si d [u]> w [vu] + d [v]
- supprimer u de q avec la distance d [u]
- d [u] = w [vu] + d [v]
- ajouter u à q avec la distance d [u]
- supprimer v de q
Si la file d' attente d'utiliser un arbre rouge-noir, où l' insertion et le retrait se produisent dans un journal (n), et la recherche de l'élément minimum de même pour log (n), la complexité de l'algorithme sera O (n log (n) + log m (n)) .
Et ici, il convient de noter une caractéristique importante: rien n'empêche, en théorie, de considérer le sommet plusieurs fois. Si le sommet a été examiné et que la distance jusqu'à celui-ci a été mise à jour à une valeur incorrecte, supérieure à la valeur réelle, alors, à condition que tôt ou tard le système converge et que la distance jusqu'à u soit mise à jour à la valeur correcte, il est permis de faire de telles astuces. Mais il convient de noter - un sommet doit être considéré plus d'une fois avec une faible probabilité.
Trier la table de hachage
Pour réduire le temps d'exécution de l'algorithme de Dijkstra à un linéaire, une structure de données est proposée, qui est une table de hachage avec des numéros de noeud (node_id) comme valeurs. Je note que le besoin du tableau d ne disparaît pas, il est toujours nécessaire d'obtenir la distance au ième nœud en temps constant.
La figure ci-dessous montre un exemple de la structure proposée.
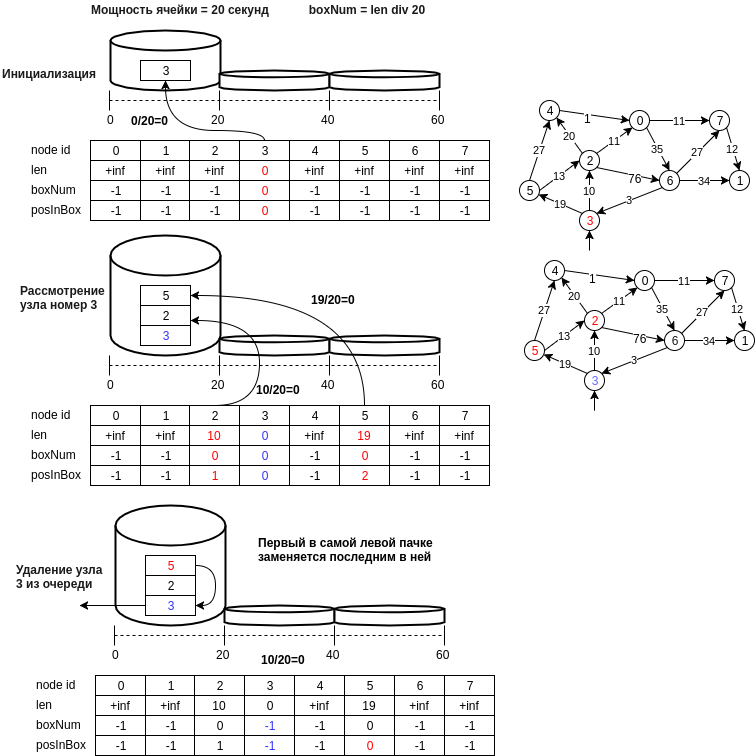
Décrivons par étapes la structure de données proposée:
- le nœud u est écrit dans la cellule avec un nombre égal à d [u] // bucket_size, où bucket_size est la puissance de la cellule (par exemple, 20 mètres, c'est-à-dire que la cellule au numéro 0 contiendra des nœuds dont la distance sera comprise entre [0, 20) mètres )
- le dernier nœud de la première cellule non vide, c'est-à-dire l'opération d'extraction de l'élément minimum sera effectuée dans O (1). Il est nécessaire de conserver l'état actuel de l'identifiant du numéro de la première cellule non vide (min_el).
- l'opération d'insertion est effectuée en ajoutant un nouveau numéro de nœud à la fin de la cellule et en exécutant également O (1), car le calcul du nombre de cellules s'effectue en un temps constant.
- l'opération de suppression, comme dans le cas d'une table de hachage, une énumération normale est possible, et on pourrait faire une hypothèse et dire qu'avec une petite taille de cellule, c'est aussi O (1). Si cela ne vous dérange pas la mémoire (en principe, et il ne faut pas beaucoup, un autre tableau par n), alors vous pouvez créer un tableau de positions dans la cellule. Dans ce cas, si l'élément est supprimé au milieu de la cellule, il est nécessaire de déplacer la dernière valeur de la cellule vers l'emplacement supprimé.
- un point important lors du choix de l'élément minimum: il n'est minimal qu'avec une certaine probabilité, mais l'algorithme examinera la cellule min_el jusqu'à ce qu'elle devienne vide et tôt ou tard l'élément réel minimum sera pris en compte, et si nous avons accidentellement mis à jour la valeur de la distance au nœud accessible à partir de minimum, alors les nœuds adjacents au minimum peuvent à nouveau être dans la file d'attente et la distance à eux sera correcte, etc.
- Vous pouvez également supprimer des cellules vides jusqu'à min_el, économisant ainsi de la mémoire. Dans ce cas, la suppression du nœud v de la file d'attente q ne doit être effectuée qu'après avoir considéré tous les nœuds adjacents.
- et vous pouvez également modifier la puissance des cellules, les paramètres pour augmenter la taille des cellules et le nombre de cellules lorsque vous devez augmenter la taille de la table de hachage.
Résultats de mesure
Des contrôles ont été effectués sur la carte osm de Moscou, déchargés via osm2po en postgres, puis chargés en mémoire. Les tests ont été écrits en Java. Il y avait 3 versions du graphique:
- graphique source - 0,43 million de nœuds, 1,14 million d'arcs
- version compressée du graphique avec 173 000 nœuds et 750 000 arcs
- version piétonne de la version compressée du graphique, 450k arcs, 100k nœuds.
Voici une image avec des mesures sur différentes versions du graphique:

Considérez la dépendance de la probabilité de revoir le sommet et la taille du graphique:
| nombre de vues de nœuds | compter les sommets | probabilité de revoir le nœud |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0,9 |
| 431490 | 419594 | 2.8 |
Vous pouvez remarquer que la probabilité ne dépend pas de la taille du graphique et est plutôt spécifique à la demande, mais elle est petite et sa plage est configurée en modifiant la puissance de la cellule. Je vous serais très reconnaissant de vous aider à construire une modification probabiliste de l'algorithme avec des paramètres garantissant un intervalle de confiance dans la plage dont la probabilité de visualisation répétée ne dépassera pas un certain pourcentage.
Des mesures qualitatives ont également été effectuées pour confirmer pratiquement la comparaison de l'exactitude du résultat des algorithmes avec la nouvelle structure de données, qui a montré une coïncidence complète de la longueur de chemin la plus courte de 1000 nœuds aléatoires à 1000 autres nœuds aléatoires sur le graphique. (et ainsi de suite 250 itérations) lorsque vous travaillez avec une table de hachage de tri et un arbre rouge-noir.
Le code source de la structure de données proposée est situé sur le lien
PS: Je connais l'algorithme Torup et le fait qu'il résout le même problème en temps linéaire, mais je n'ai pas pu maîtriser ce travail fondamental en une soirée, même si j'ai compris l'idée en termes généraux. Au moins, si je comprends bien, une autre approche y est proposée, basée sur la construction d'un arbre couvrant minimal.
PSS Dans une semaine, j'essaierai de trouver l'heure et de faire une comparaison avec le bouquet Fibonacci et d'ajouter un peu plus tard le navet github avec des exemples et des codes de test.